多元零膨胀Poisson-Lindley分布

熊朝松，黄希芬

多元零膨胀Poisson-Lindley分布

熊朝松，黄希芬

（云南师范大学 数学学院，云南 昆明 650500）

零值过多的多元计数数据出现在生活中的各个领域，这类数据成为了统计学研究的一个热点．基于随机表示提出了一个新的多元零膨胀Poisson-Lindley分布，主要用于研究存在过度分散的多元计数数据，进一步讨论了其相关统计性质，构造EM算法获得参数的极大似然估计．通过2组随机模拟试验验证了参数估计方法能得到稳定有效的结果，真实数据分析结果表明，多元零膨胀Poisson-Lindley分布在数据处理中具有较强的实用性．

多元计数数据；随机表示；多元零膨胀Poisson-Lindley分布；EM算法

实际生活中经常能观测到许多非负整数的计数数据，这类数据广泛存在于临床医学、公共卫生、生态环境、生物研究、金融保险、计量经济学和农牧业等诸多领域，具有重要的研究价值和实际意义．目前，对于观测到的计数数据，学者们普遍利用统计学中的经典离散分布进行分析研究，如Poisson分布和Negative Binomial分布等．然而，在生产生活中会产生各式各样的数据，其中有很多数据不具备经典离散分布的结构，因此不能很好地被拟合分析．为了应对不同类型的计数数据，学者们通过广义一般化、混合模型、复合技术和离散化连续分布等方法开发出了不同的离散分布，如广义Poisson分布、有限维混合分布[1]、离散化泊松-指数混合分布[2]等．Sankaran[3]利用复合技术，在假设Poisson分布的参数服从Lindley分布[4]形式的条件下，得到了一个单参数的离散Poisson-Lindley分布．由于该分布的期望小于其方差，因此在拟合过度分散的计数数据时，具有很好的灵活性．在Sankaran提供的实例分析中Poisson-Lindley分布比Poisson分布拟合得更好，且与双参数的Hermite分布和Negative Binomial分布的拟合效果大致相同．该离散分布的提出为模拟计数数据提供了一个新的有效思路，并在大量的实践中验证了其优秀的拟合效果[5-6]．

在实际遇到的计数数据中，过量零的出现引起了人们的关注，这类数据中零值的数量超过了一般离散分布随机产生的数量，呈现出过分散特征，学者们将此现象称为零膨胀（zero-inflated，ZI）现象．用于分析零膨胀数据的零膨胀模型具有很长的研究历史，最早可以追溯到20世纪60年代，直至今日仍是统计学研究的热点．Cohen[7]讨论了零膨胀Poisson（ZIP）分布；Lambert[8]等讨论了带有协变量的ZIP回归模型并应用于制造缺陷数据；Minami[9]等研究了零膨胀Negative Binomial（ZINB）分布模型，并利用其对鲨鱼捕获数据进行建模分析；在文献[3]提出的Poisson-Lindley分布模型的基础上，Xavier[10]等拓展了适用于零膨胀和零欠缺（zero-deflated）情形的零修正Poisson-Lindley（ZMPL）分布模型，并在2组真实数据中验证了ZMPL模型的良好效果．

在观测到零膨胀计数数据的同时，往往包含了不同方面的记录情况，同时这些不同方面的数据之间存在一定的关系．如在制造业中制造产品时发生不同类型缺陷的数量，在车祸事故中不同情况伤害（财产或人身）的数量等．此时如果分别使用一元的分布模型拟合多方面数据，得到的分析结果往往无法解释其中隐藏的数据关联，显得过于片面，因此开发多元零膨胀计数模型是必要的．Li[11]等提出了一个多元零膨胀Poisson分布来建模分析制造业数据中过多零的情况；Gomez[12]等讨论了Poisson-Lindley分布的多元情况，能够应用于边际过度离散的多元相关计数数据，并给出了该多元分布的相关性质和估计方法；Liu[13]等利用随机表示构造了一种新的多元ZIP分布，相对于文献[11]所给的多元零膨胀Poisson分布，该分布在数据分析中拟合性能更好．受到文献[13]所考虑的多元零膨胀Poisson分布的启发，本文利用随机表示开构造了多元零膨胀Poisson-Lindley分布（多元ZIPL分布），来拟合更多的多元零膨胀计数数据．同时，给出多元ZIPL分布的相关统计性质及其参数估计方法，利用自助抽样法构造估计的置信区间．最后，通过随机模拟试验和一组真实数据来评估多元ZIPL分布的性能．

1　多元零膨胀Poisson-Lindley分布

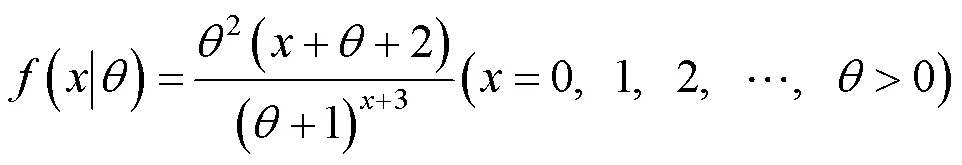
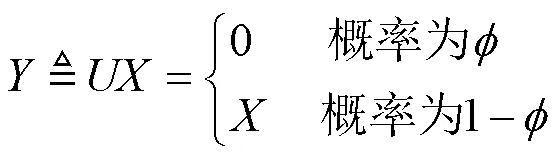
1.1 概率质量函数和累积分布函数

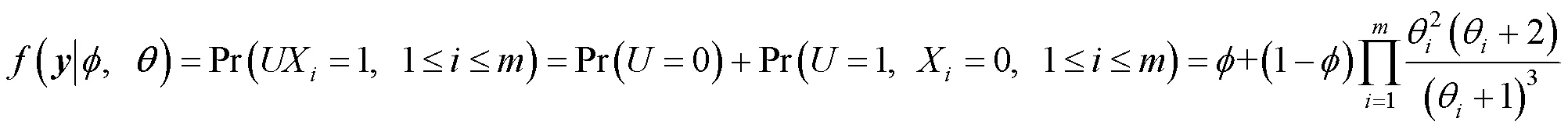
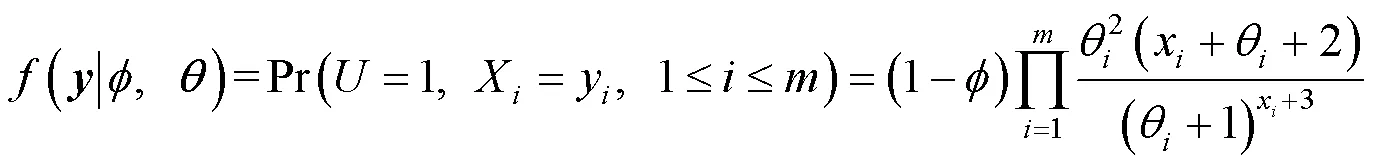
综上可知

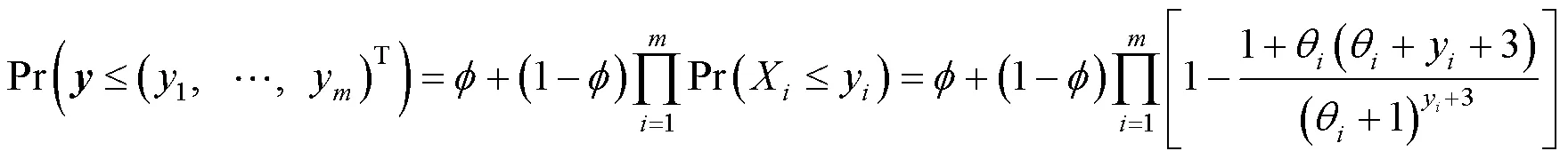
1.2　混合矩和矩生成函数

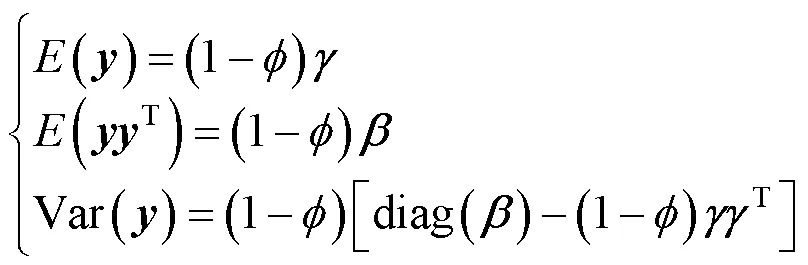
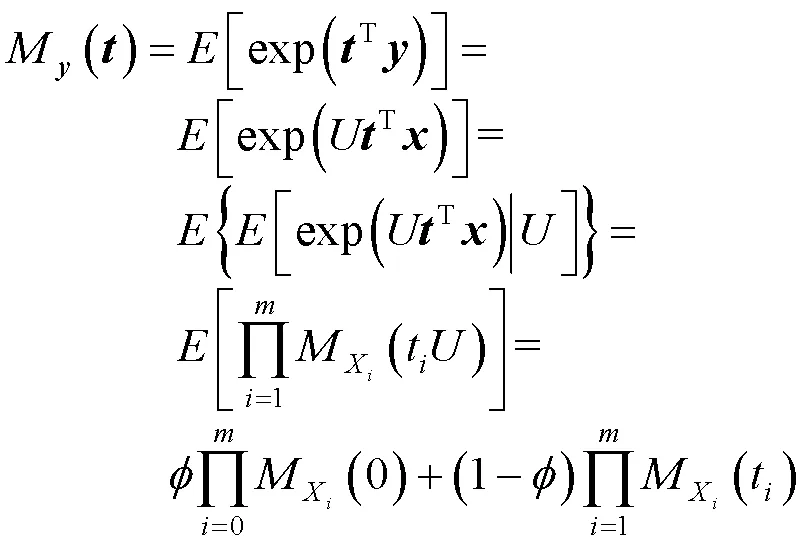
1.3 边际分布

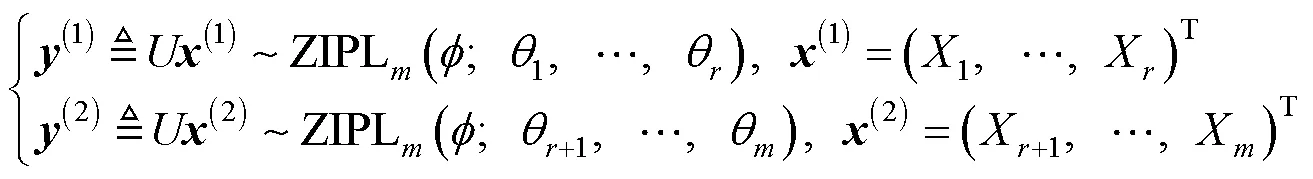
2 似然推断

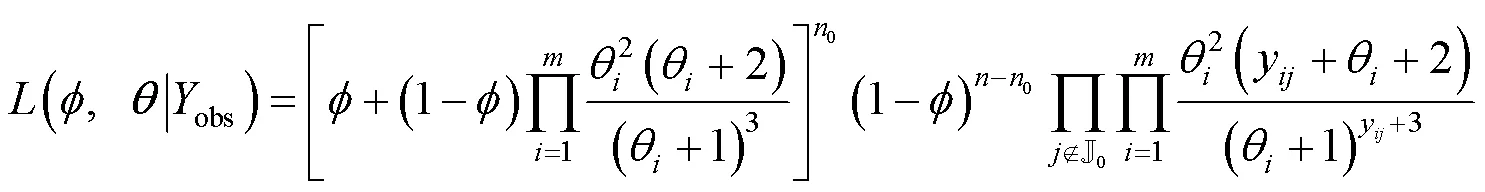
2.1 EM算法

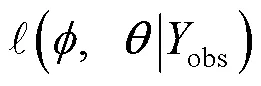
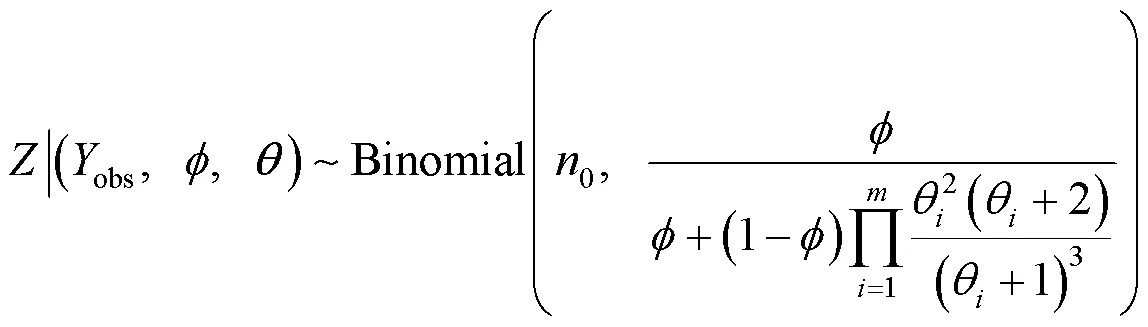
对应的对数似然函数为

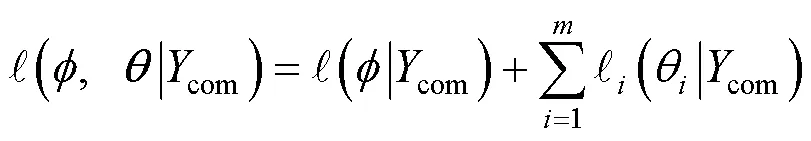
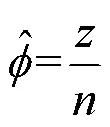
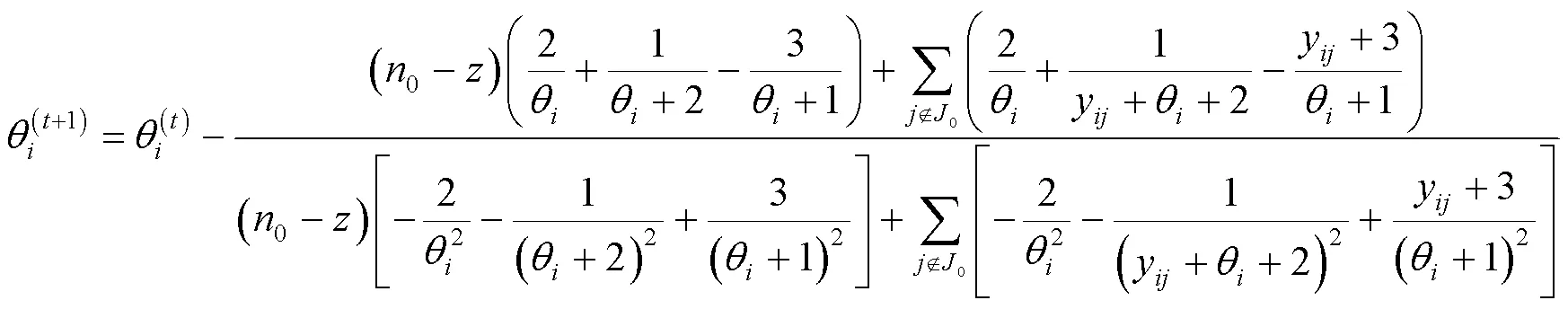
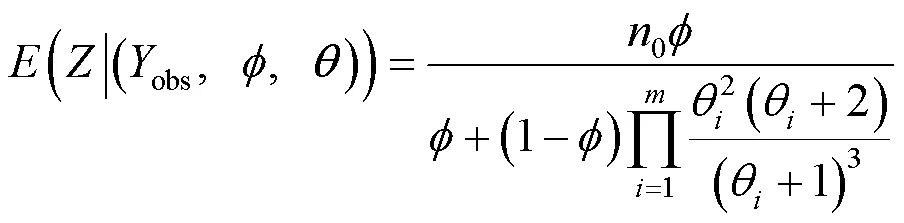
2.2 自助抽样置信区间

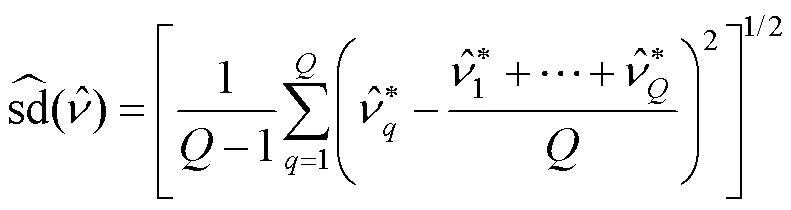
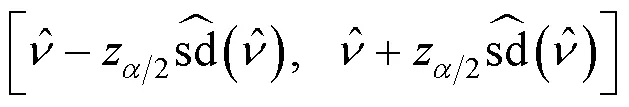
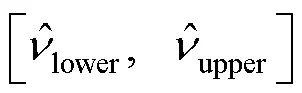
3　随机模拟

每组实验重复进行1 000次模拟，计算出参数估计的平均偏差（BIAS）和均方误差（MSE），最终结果见表1～2．

表1　第１组实验二元ZIPL分布参数极大似然估计结果

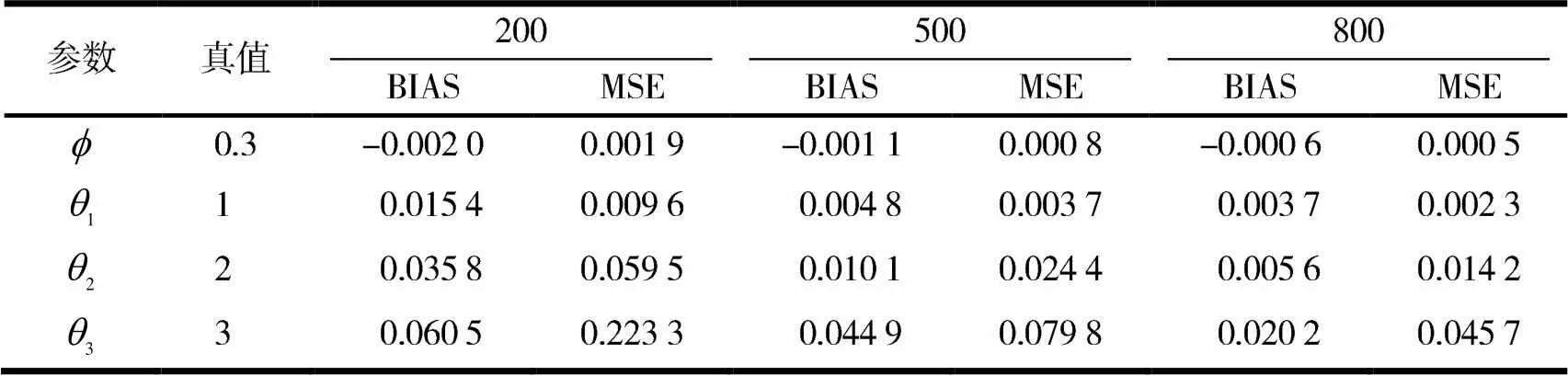
表2　第2组实验三元ZIPL分布参数极大似然估计结果

由表1～2可以看出，在不同组合下参数估计值均能收敛到给定的真值．同时，随着样本的增加，BIAS和MSE均在减小，表明参数估计的效果越来越好，越稳定地接近真实值．

4　实例分析

4.1 澳大利亚健康调查数据

利用本文提出的模型方法研究Cameron[15]等提供的一项健康调查数据的一个子集，过去两天的处方药总数和非处方药物总数．网站http://cameron.econ.ucdavis.edu/racd2/RACD2programs.html可以获取到关于原始数据集的具体细节．

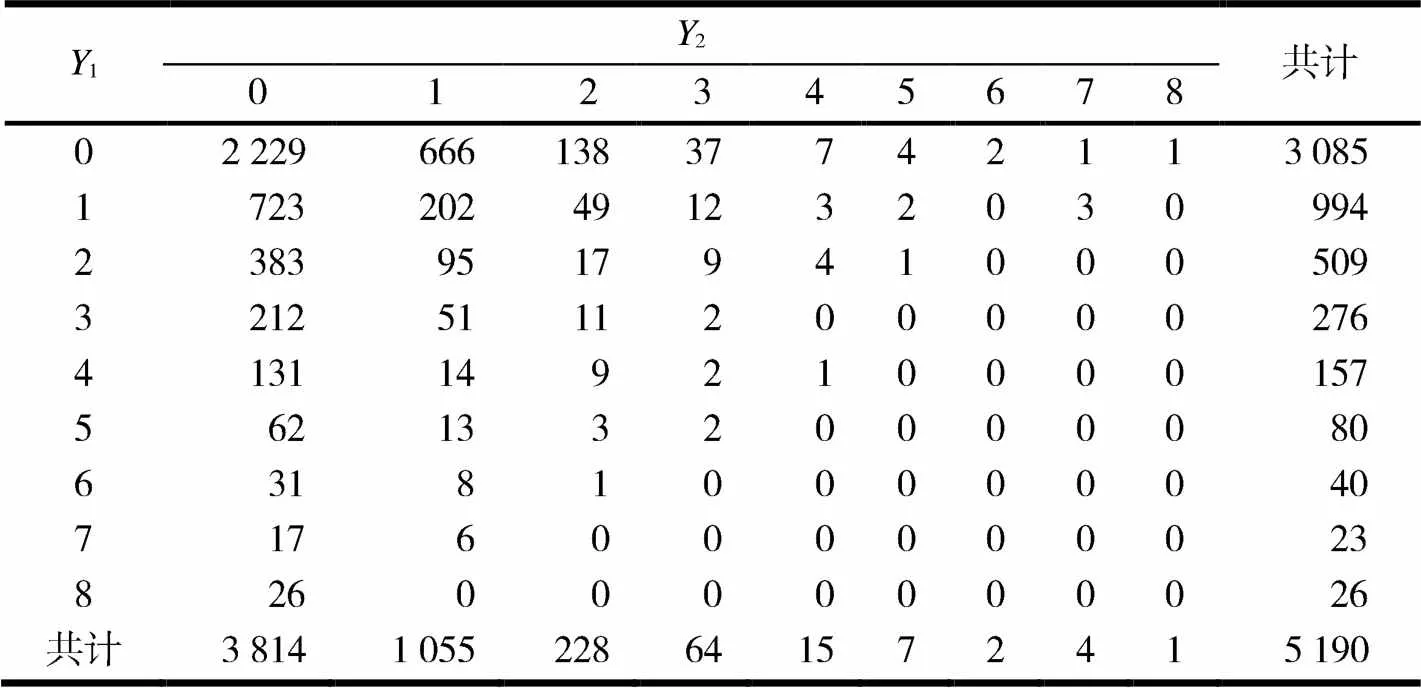
表3　处方药总数和非处方药物总数的交叉表

各个参数的极大似然估计（MLE），自助抽样样本的标准差（SD），以及2种置信水平为95%自助抽样置信区间见表4．

表4　参数的极大似然估计值及其置信区间

注：95%自助抽样置信区间I由式（12）计算得到；95%自助抽样置信区间II由式（13）计算得到．

4.2 模型选择

分别使用了二元零膨胀Poisson分布[12]和二元Poisson-Lindley分布[13]拟合此数据集，并与本文提出的二元零膨胀Poisson-Lindley分布进行比较，采用Akaike 信息准则（AIC）和Bayes 信息准则（BIC）验证本

文提出的模型的有效性．各模型模拟的AIC和BIC值见表5．

表5　模型选择结果

由表5可以看出，二元零膨胀Poisson-Lindley分布的AIC和BIC值均小于其他2个模型，表明本文提出的分布模型拟合效果更好，更适用于该数据集．

5 结语

本文根据随机表示提出了结构简单、解释性强的多元零膨胀Poisson-Lindley分布模型，研究了包括概率质量函数、累积分布函数，矩和矩生成函数，边际分布等在内的统计性质．利用EM算法研究了多元零膨胀Poisson-Lindley分布似然推断，推导出了方便计算的参数估计式，并通过2组仿真模拟验证了估计的有效性．利用提出的模型进行实例分析，在与其它2种模型比较中，AIC和BIC模型选择方法均选择了本文所提出的二元零膨胀Poisson-Lindley分布．在今后的研究中，为了适应生活中更多的多元计数数据，可以考虑多元零调整Poisson-Lindley分布拟合零过多和零欠缺情况．

[1] 全星澄，李巍．基于EM算法的有限维混合分布参数估计研究[J]．统计与决策，2017，33（12）：25-29．

[2] 任美芳，刘禄勤．离散化泊松-指数混合分布的性质和参数估计[J]．统计与决策，2019，35（19）：25-29．

[3] Sankaran M．The discrete Poisson-Lindley distribution[J]．Biometrics，1970，26（1）：145-149．

[4] 刘晏辰，代莹，王蓉华，等．Lindley分布的统计分析[J]．统计与决策，2017，33（18）：77-80．

[5] Ghitany M E，Al-Mutairi D K．Estimation methods for the discrete Poisson–Lindley distribution[J]．Journal of Statistical Computation & Simulation，2009，79（1）：1-9．

[6] Al-Babtain A A，Gemeay A M，Afify A Z．Estimation Methods for the Discrete Poisson-Lindley and Discrete Lindley Distributions with Actuarial Measures and Applications in Medicine[J]．Journal of King Saud University - Science，2021，33（2）：101224．

[7] Cohen A C．Estimation in mixtures of discrete distributions[C]//Classical and contagious discrete distributions．Calcutta： Statistical Pub. Society，1963：373-378．

[8] Lambert D，Zero-Inflated P R．With an Application to Defects in Manufacturing[J]．Technometrics，1992，34（1）： 1-14．

[9] Minami M，Lennert-Cody C E，Gao W，et al．Modeling shark bycatch：The zero-inflated negative binomial regression model with smoothing[J]．Fisheries Research，2007，84（2）：210-221．

[10] Xavier D，Santos-Neto M，Bourguignon M，et al．Zero-Modified Poisson-Lindley distribution with applications in zero-inflated and zero-deflated count data[J/OL]．Methodology，2017（12）[2017-12-12]．https://arxiv.org/abs/1712.04088．

[11] Li C S，Lu J C，Park J，et al．Multivariate Zero-Inflated Poisson Models and Their Applications[J]．Technometrics，1999，41（1）：29-38．

[12] Gomez-Deniz E，Sarabia J M，Balakrishnan N．A multivariate discrete Poisson-Lindley distribution：extensions and actuarial applications[J]．ASTIN Bulletin，2012，42（2）： 655-678．

[13] Liu Y，Tian G L．Type I multivariate zero-inflated Poisson distribution with applications[J]．Computational Statistics & Data Analysis，2015，83：200-222．

[14] 王博．基于EM算法的多水平零膨胀负二项混合效应回归模型的参数估计[J]．高师理科学刊，2019，39（3）：10-14．

[15] Cameron A C，Trivedi P K．Regression analysis of count data[M]．2nd ed．New York：Cambridge university press，2013．

Multivariate zero-inflated Poisson-Lindley distribution

XIONG Chaosong，Huang Xifen

（School of Mathematics，Yunnan Normal University，Kunming 650500，China）

Multivariate count data with excessive zero values appear in various fields of life，and this kind of data has become a hot spot in statistical research．Based on random representation，a new multivariate zero-inflated Poisson-Lindley distribution is proposed，which is mainly used to study multivariate count data with excessive dispersion，and its related statistical properties are further discussed．Finally，the EM algorithm is constructed to obtain the maximum likelihood estimation of parameters．Two groups of random simulation experiments show that the parameter estimation method can obtain stable and effective results．The real data analysis results show that the multivariate zero-inflated Poisson-Lindley distribution has strong practicability in data processing．

multivariate count data；stochastic representation；multivariate zero-inflated Poisson-Lindley distri-

1007-9831（2022）05-0005-07

O212

A

10.3969/j.issn.1007-9831.2022.05.002

bution；EM algorithm

2021-12-03

熊朝松（1997-），男，湖北荆门人，在读硕士研究生，从事数理统计研究．E-mail：chsoxiong@163.com

黄希芬（1988-），女，云南昆明人，讲师，博士，从事生存分析研究．E-mail：xf_yellow@126.com