基于B样条的概率密度函数非参数估计
2022-06-24张梦珠王旭辉
张梦珠, 王旭辉
(合肥工业大学数学学院,合肥230601)
1 引 言
概率论与数理统计研究的对象是随机现象,随机变量的引进使得对随机现象结果进行定量的数学处理成为可能.给定一个随机变量,其概率分布情况有着广泛的应用[1].因此获取其概率分布情况是一个值得研究的课题.在连续型随机变量中,密度函数是一个核心概念[2].现实生活中大量复杂问题其状态受到内在和外在双重因素的影响,为了掌握这类事物的内在规律并对未来可能发生的状态变换作出预测,就需要通过数据分析、概率建模等方式,寻找一个概率分布.了解随机变量的概率分布有助于计算分布的均值、方差和进行结构可靠性分析或风险分析[3].此外,银行学、经济学、生理学等都以概率密度函数估计为基础,展开对所在领域的知识和问题的探讨与研究[4].但实际生活中,随机变量的概率分布一般是未知的.事实上,所获得的只是一个观察样本.假设这些数据点是一个未知概率密度函数的样本,概率密度估计就是从观测数据中构造密度函数的估计.
概率密度函数估计方法主要有三类:参数化方法、非参数化方法和半参数估计方法.参数概率密度函数估计,总是假设概率密度函数的参数形式已知[5],但在实际问题中参数形式的假设可能会产生误导的结论或结果.而本文要讨论的非参数密度估计可以避免概率建模和推理中的参数假设,从而为上述问题提供了新的解决思路[6].非参数密度估计方法不需要对点样本分布的参数形式做事先的假设,而仅仅从采样数据本身对概率密度函数做出估计.半参数估计是将参数化估计与非参数化估计相结合的一种方法.非参数密度估计是一个持久和不断发展的研究领域,在金融、金融计量经济学、物理和社会科学等学科中有着广泛的应用,它提供了参数化方法的另一种选择,在数据建模中实现了更大的灵活性,降低了模型误用的风险.本文重点讨论的是单变量密度函数的非参数估计.
20世纪以前,参数化的概率密度函数估计方法得到了广泛的应用.到了20世纪上半叶,不需要对总体特征作假设的非参数统计方法迅速发展起来[7].自20世纪50年代以来,已经出现了一些强大的方法来提高概率密度估计的性能,而不仅仅是简单的直方图表示,还包括正交序列、核函数和样条三类非参数估计方法.直方图估计的缺点是它的形状取决于样本范围划分的宽度的主观选择,且直方图密度估计在高维空间很少有实效.参考文献[8-10]研究的正交序列估计方法用正交级数(如埃尔米特、傅立叶或三角标准正交函数系)展开逼近概率密度函数.但其主要缺点是得到的估计结果无法保证满足概率密度函数条件(非负且积分为1).关于核密度估计的文献很广泛,包括Fix、Hodges[11]、RosenBlatt[12]等.相比于传统直方图,核密度估计不仅能更好地分析所研究的概率分布,而且可以生成概率密度函数的平滑估计[13].核函数的形状和平滑系数是核估计的两个基本概念,其中平滑系数是核估计的关键.此外,参考文献[14]提出了一种局部基的非参数密度估计方法,结合基对偶理论介绍了基于有限维B样条基投影的伽辽金方法.
本文结合非参数密度估计方法,提出了从给定的数据样本中识别连续随机变量的概率密度函数的方法,在信息熵的无偏估计的基础上,利用内点法优化得到了B样条基函数的对应系数.在数值实验部分,本文将基于B样条的概率密度估计方法与经典的核密度估计方法以及正交序列估计方法进行了对比.此外,本文讨论了两个评价指标MAE,MSE用来评估模型的拟合程度.实验结果表明,基于B样条的概率密度估计方法取得了较优估计效果.
2 预备知识
定义1B样条基函数的定义如下:
设U=[u0,u1,…,um+k+1]是非递减实数序列,即ui≤ui+1(i=0,1,…,m+k),其中ui称为节点,U称为节点序列.第i个k次(k+1阶)B样条基函数Ni,k(t)的递归定义如下:
(1)

定义2给定节点向量U=[u0,u1,…,um+k+1],则B样条函数的定义为
其中di∈R(i=0,1,…,m)为控制系数,Ni,k(t)(i=0,1,…,m)为(1)式定义的B样条基函数.
3 B样条函数的概率密度估计
给定概率密度函数一个随机样本,设其样本容量为N.采样点记为yt(t=1,2,…,N),其中p=min{y1,y2,…,yN},q=max{y1,y2,…,yN}.
本文使用二次B样条函数
(2)

(i)βj≥0 (j=1,2,…,M);

(3)
为了便于计算,将节点向量选取为
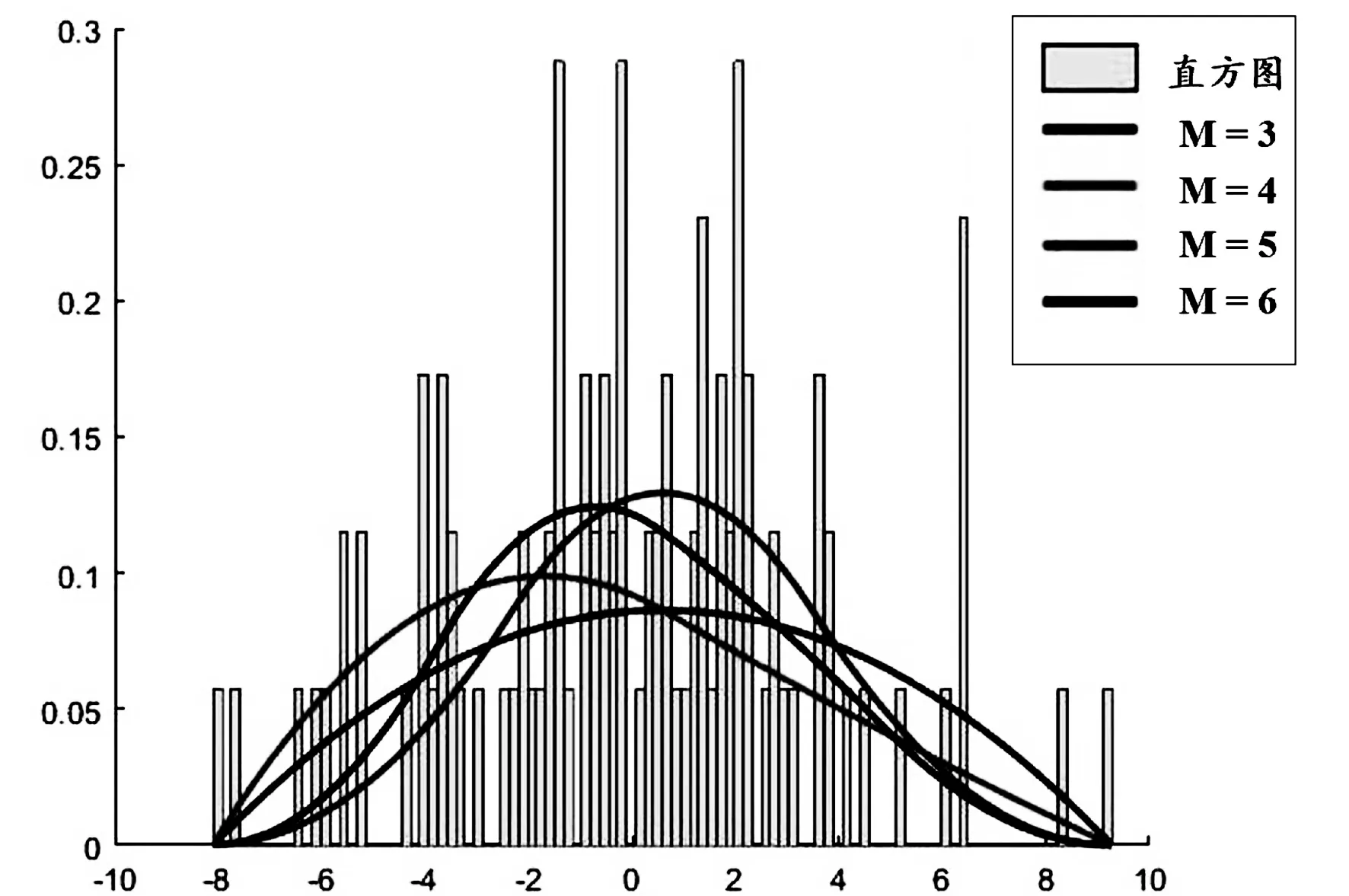
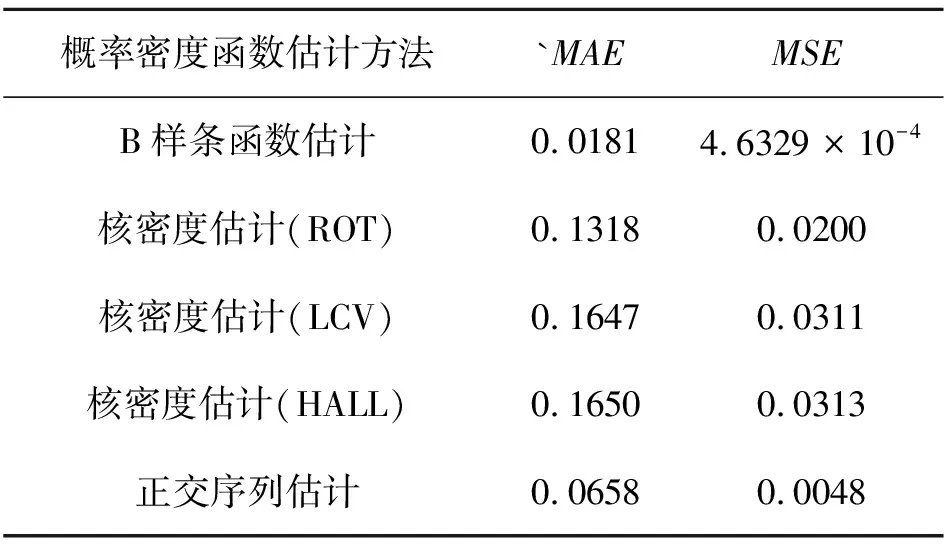
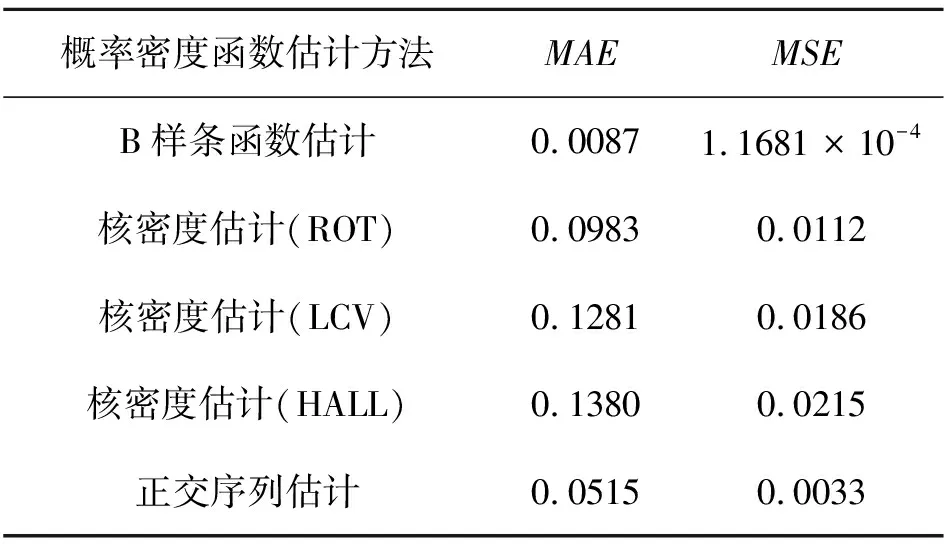
U=[p,p,p,u1,u2,…,un,q,q,q],u1 则(3)式可表示为 (4) (5) (6) 进而,概率密度函数Φ(y)的最佳估计问题可转换为如下的优化问题: (7) (7)式是一个带有约束条件的非线性规划问题,求解约束非线性规划问题的方法主要有Lagrange乘数法、可行方向法、惩罚函数法等方法[15].本文利用内点法解决该优化问题. 注 文中选择了二次B样条基函数进行估计,也可将其推广至其它次数B样条情形. 本节对一些模拟采样数据,针对其概率密度函数进行B样条估计,求解优化问题(7)得到的解为B样条基函数的对应系数,从而得到一个估计模型.为了说明本文方法的有效性,与经典的核密度估计方法(核函数为高斯函数)以及正交序列估计方法(傅里叶为正交级数)进行了对比.对于核密度估计方法[13],文中采样了三种策略进行带宽选择,依次为ROT[13],LCV[13],HALL[16].实验中,本文讨论了MAE,MSE两个评价指标,其中MAE为平均绝对误差,MSE为均方误差,其计算公式为: 本节实例中样本量均为800,即N=800,样本点记为y1,y2,…,yN.记p=min{y1,…,yN},q=max{y1,…,yN}. 例1随机变量Y的概率密度函数ΦY~N(0,4). 以ΦY~N(0,4)为例说明基函数个数M是如何选取的.熵的无偏估计ME越小越好,选取与其对应的基函数个数M作为估计模型中B样条基函数的个数.图1表示的是选取不同的基函数个数M得到的拟合结果.由表1知,当基函数个数M=5拟合效果最佳. 图1 ΦY~N(0,4)的拟合结果 表1 密度函数ΦY~N(0,4)的计算结果 例2随机变量Y的概率密度函数ΦY~χ2(3). 图2 ΦY~χ2(3)的拟合结果 表2 密度函数ΦY~χ2(3)的计算结果 例3随机变量Y的概率密度函数ΦY~0.5N(0,1)+0.5N(4,1). 图3 ΦY~0.5N(0,1)+0.5N(4,1)的拟合结果 表3 密度函数ΦY~0.5N(0,1)+0.5N(4,1)的计算结果 图4 ΦY~N(0,3)的拟合结果 表4 密度函数ΦY~N(0,3)的计算结果 数值实验结果表明,由内点法作为系数矢量的优化策略的B样条函数估计方法取得了不错的效果.由图2到图4和表2到表4,拟合效果以及评价指标MAE,MSE两方面都表明:本文给出的估计方法相较于核密度估计方法与正交系列估计方法有更好的估计表现.但是该方法效率比较低,下一步工作将在此基础上对如何让进一步缩短计算时间展开研究.此外,文中选择了二次B样条基函数进行估计,也可将其推广至其它次数B样条情形. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.



3 数值实例




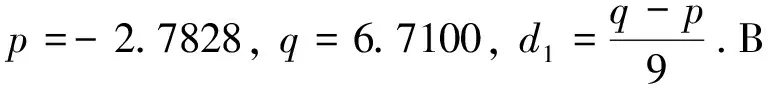




4 结 论
