矩阵弱相似的一个充要条件

赵紫晶， 张 楠， 陈惠香

(扬州大学数学科学学院，江苏扬州225002)

1 引 言

矩阵弱相似的定义最早出现在文献[1]中，设k是一个域，A，B∈Mn(k)是域k上的n×n-矩阵，若存在n×n-可逆矩阵C∈GLn(k)及非零纯量0≠α∈k，使得CAC-1=αB，则称A与B弱相似.显然，相似的矩阵是弱相似的，并且弱相似是矩阵之间的一个等价关系.矩阵弱相似的概念应用很广泛，例如在研究矩阵代数的群作用和Hopf代数作用时，人们会用弱相似给出作用的等价分类. 文献[2]研究M3(k)的kS3-模代数结构时，利用矩阵弱相似给出了分类. 文献[3]研究李代数的包络代数的广义Hopf-Ore扩张时，利用矩阵弱相似给出了同构分类[4]. 有关Hopf代数及其作用理论的基本概念可参阅参考文献[5-6]. 上述参考文献都是基于矩阵弱相似的前提下进行相关研究，但是关于弱相似内在刻画的研究在文献中尚未提到. 在本文将讨论这一问题，研究矩阵的弱相似关系，尝试给出矩阵弱相似的等价条件.

2 预备知识

由若尔当块组成的准对角矩阵

称为若尔当形矩阵.以下结论是已知的，见文献[7].

引理1每个n阶复数方阵A都与一个若尔当形矩阵相似，这个若尔当形矩阵除去其中若尔当块的排列次序外是被矩阵A唯一决定的，称为A的若尔当标准形.

3 矩阵弱相似

引理2设n是正整数，λ0，α∈且α≠0，则αJ(λ0，n)与J(αλ0，n)有相同的初等因子组，从而它们相似.

证直接计算可知，αJ(λ0，n)的初等因子组为(λ-αλ0)n，所以αJ(λ0，n)与J(αλ0，n)有相同的初等因子组，从而它们相似.

命题1设A是n阶方阵，0≠α∈.若矩阵A的全体互异特征值为λ1，λ2，…，λs，对应代数重数分别为k1，k2，…，ks，则矩阵αA的全体互异特征值为αλ1，αλ2，…，αλs，对应代数重数分别为k1，k2，…，ks.

证由假设条件知，k1+k2+…+ks=n，且A的特征多项式为

|λI-A|=(λ-λ1)k1(λ-λ2)k2…(λ-λs)ks.

因此αA的特征多项式为

|λI-αA|=|α(α-1λI-A)|=αn(α-1λ-λ1)k1(α-1λ-λ2)k2…(α-1λ-λs)ks

=(λ-αλ1)k1(λ-αλ2)k2…(λ-αλs)ks.

所以αA的全体互异特征值为αλ1，αλ2，…，αλs，对应重数分别为k1，k2，…，ks.

定理1设两个n阶方阵A，B的初等因子组分别是(λ-λ1)k1，(λ-λ2)k2，…，(λ-λs)ks和(λ-η1)l1，(λ-η2)l2，…，(λ-ηt)lt， 则A与B弱相似的充分必要条件是s=t，且存在一个非零复数α以及1，2，…，s的一个置换σ，使得(λ-λσ(i))kσ(i)=(λ-αηi)li，即λσ(i)=αηi，kσ(i)=li，1≤i≤s.

证必要性.设A，B弱相似，则存在非零纯量α∈使得A与αB相似，因此A与αB有相同的初等因子组.由于B的初等因子组为(λ-η1)l1，(λ-η2)l2，…，(λ-ηt)lt，所以B的若尔当标准形为

因此αB与αJB相似.由此得A与αJB相似，从而A与αJB有相同的初等因子组.由引理2知，αJB的若尔当标准形为

因此αJB的初等因子组为(λ-αη1)l1，(λ-αη2)l2，…，(λ-αηt)lt.这样由假设条件知s=t，且存在1，2，…，s的一个置换σ使得

(λ-λσ(i))kσ(i)=(λ-αηi)li， 1≤i≤s.

充分性.设s=t，且存在一个非零复数α以及1，2，…，s的一个置换σ，使得

(λ-λσ(i))kσ(i)=(λ-αηi)li， 1≤i≤s.

由必要性的证明知αB的初等因子组为(λ-αη1)l1，(λ-αη2)l2，…，(λ-αηt)lt，因此A与αB有相同的初等因子组，所以A与αB相似，从而A与B弱相似.

定义1设A是一个n阶复方阵，若A的若尔当标准形为

则称序列(λ1，k1)，(λ2，k2)，…，(λs，ks)为矩阵A的特征序列.

由定理1，有如下推论.

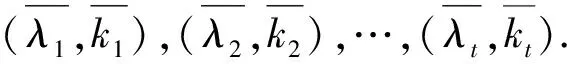
4 结 论

矩阵的弱相似是矩阵相似概念的推广，起源于分次环的研究，在群作用和广义Hopf-Ore扩张等理论的研究中有广泛应用，因此矩阵弱相似的内在刻画是有意义的研究课题.本文主要研究复数域上矩阵的弱相似关系，首先从相似矩阵初等因子组之间的关系出发，描述了一个矩阵与其非零纯量倍矩阵的特征值及其代数重数之间的对应关系，然后利用初等因子组给出了两个矩阵弱相似的一个等价刻画，最后引入矩阵的特征序列，并用特征序列刻画了矩阵的弱相似关系.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.