钢桁腹混凝土组合梁挠度计算方法研究

陈建兵,蒋明利,周 晨,匡冠桦

(1. 苏州科技大学 土木工程学院，江苏 苏州 215011； 2. 中交一公局第二工程有限公司，江苏 苏州 215011)

0 引 言

钢桁腹混凝土组合梁桥是近年来新兴的弱腹式钢-混组合结构桥梁，构造形式如图1。其特点是用钢桁腹杆代替传统的混凝土箱梁腹板，解决了传统箱梁腹板容易开裂的问题，并有效减少了箱梁的自重。钢管桁架可工厂化预制，施工方便，并有造型美观、侧面通透性好等优点[1]。

为适应钢桁腹混凝土组合梁在桥梁建设中的发展，国内学者对钢桁腹混凝土组合梁的变形计算进行了研究。张岩等[2]通过对钢桁腹杆的纵向弹性模量研究,得出钢桁腹杆的纵向弯曲刚度非常小，可近似认为其抗弯作用仅由混凝土顶、底板承担；黄华琪等[3]为了能够使组合梁采用统一的截面进行结构分析，提出了组合截面等效抗弯惯性矩的概念，并推导了组合截面等效抗弯惯性矩的计算公式；王彤等[4]在对桁腹式组合桁梁结构计算理论的研究中，提出根据剪切变形相等的原则，将不连续的钢桁腹杆等效成连续的钢腹板，再运用薄壁箱梁理论对该类型结构进行分析；张元海等[5]通过分析剪力滞效应对箱梁挠度的影响，提出了薄壁箱梁在考虑剪力滞影响下的挠度公式。笔者将利用换算薄壁箱梁法，按照剪切变形相等原则，对钢桁腹杆进行换算，利用Timoshenko梁理论与能量变分原理，拟提出在考虑剪切变形影响下，钢桁腹混凝土组合梁沿跨径任意位置挠度的计算方法。

图1 构造示意Fig. 1 Structure diagram

1 钢桁腹杆的等效换算

采用换算薄壁箱梁法，按剪切变形相等原则对钢桁腹杆进行换算，换算方法如图2(a)。长度为d的钢桁腹杆，其竖向高度和水平投影分别为h和b，将其换算成边长为h和b的薄钢板，等效换算后的结果如图2(b)。

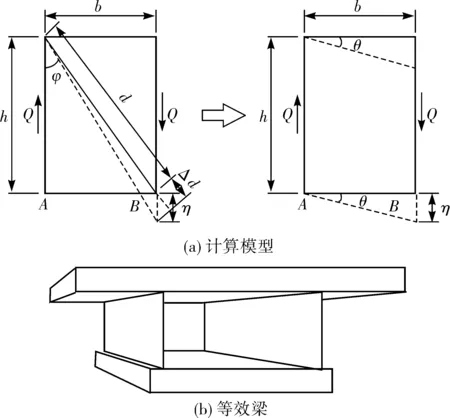
图2 等效钢腹板的换算Fig. 2 Conversion of equivalent steel web

单根钢桁腹杆受到剪力Q作用时，节点B和节点A会发生竖向移动,相对位移为η，则：

(1)

式中：Δd为钢桁腹杆伸长量；φ为钢桁腹杆的竖向夹角；Ew为钢桁腹杆的弹性模量；Ad为钢桁腹杆的截面面积。

边长为h和b的薄钢板受到剪力Q作用时，节点B和节点A的相对竖向位移为η，则：

(2)

式中：Gw为钢桁腹杆的剪切模量；t为等效钢腹板厚度。

根据剪切变形相等原则，即式(1)、式(2)相等，得：

(3)

尽管钢桁腹杆的弹性模量比混凝土的弹性模量大，考虑其提供的抗剪面积却很小，钢桁腹杆的剪切变形对钢桁腹混凝土组合梁的挠度不可忽略。

2 基于剪切变形规律的剪滞翘曲位移函数

钢桁腹混凝土组合梁在竖向荷载作用下，会发生竖向的弯曲变形，包括3个部分：铁木辛柯梁理论变形、欧拉伯努利梁理论变形、剪力滞翘曲变形，如图3。

图3 箱梁竖向荷载下的变形Fig. 3 Deformation of box girder under vertical load

其竖向位移可用公式表达为：

U(x,y,z)=-zw′(x)+zα(x)+f(y,z)u(x)

(4)

式中：z为梁上一点的z轴坐标；w′(x)为梁体竖向位移w(x)引起的纵向位移转角，即欧拉-伯努利理论梁变形；α(x)为箱梁剪切变形引起的转角,即铁木辛柯梁理论变形；f(y,z)为箱梁截面剪力滞翘曲位移函数；u(x)为顶、底板翘曲位移差。

式(4)中w′(x)和u(x)为待求变量。α(x)为反应钢桁腹混凝土组合梁在其面内的剪切位移函数，其表达式为：

(5)

式中：Q(x)为截面剪力；Aw为未埋入混凝土的等效钢腹板的截面面积。

f(y,z)为反应箱梁顶、底板在其面内的翘曲位移函数，需要提前定义。定义顶、底板的翘曲位移函数为经典的三次抛物线[7]，则：

(6)

式中：b1和b3分别为顶板和底板的内侧宽度；b2为悬臂板的宽度；h1和h2分别为顶板形心和底板形心到组合截面形心的距离，如图4；ξ为满足截面轴向内力平衡引入的应力均匀函数，由轴向内力平衡条件可得：

(7)

式中：As为箱梁横截面面积；At、Ac、Ab分别为箱梁顶板、两侧悬臂板、底板的面积。

图4 箱梁截面尺寸示意Fig. 4 Schematic diagram of box girder section size

引入截面特征值Iu、If和Af，Iu为剪滞翘曲惯性矩，If为剪滞翘曲惯性积，Af为剪滞翘曲面积。计算公式为[10]：

(8)

(9)

(10)

3 能量变分法计算

3.1 基本微分方程的建立

在对钢桁腹混凝土组合梁进行变形计算前，做如下假定：

1)忽略钢桁腹杆的纵向弯曲刚度，其纵向弯曲应变能仅由混凝土顶、底板承担。

2)钢桁腹混凝土组合梁顶、底板及悬臂板在竖向荷载作用下满足平截面假定。

3)忽略钢桁腹混凝土组合梁顶、底板及悬臂板的竖向应变和横向应变及其面外的剪切应变。

4)钢桁腹混凝土组合梁在弹性工作范围内，忽略钢筋的影响。

根据最小势能原理，当结构处在平衡状态时，体系总势能的一阶变分为零[14]，即：

δ(V-W)=0

(11)

式中：V为体系的应变能；W为外力势能；δ(·)是一阶变分函数。

梁受弯时的外力势能:

(12)

式中：l为钢杵腹混凝土组合梁的计算跨径；M(x)为外荷载作用下的梁段弯矩；φ′为弯矩作用产生的变形，其表达式为：

φ′=w′(x)-α(x)

(13)

箱梁的应变能包括腹板、顶板、底板及悬臂板的应变能。顶板、底板及悬臂板的应变能可表示为：

(14)

式中：ψ=1,2,3，分别代表顶板、底板和悬臂板；E为混凝土的弹性模量；Gc为混凝土的剪切模量；ε为弯曲应变；γ为剪切应变。ε、γ的表达式为：

(15)

等效钢腹板的应变能表示为：

(16)

钢桁腹混凝土组合梁整体的应变能为：

(17)

式中：I为竖向弯曲惯性矩。

将式(12)、式(17)带入式(11)，利用变分原理，可得控制微分方程及边界条件：

(18)

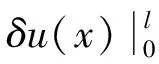
(19)

由式(19)的边界条件，整理可得:

(20)

式中：k0和k为瑞纳斯参数，其表达式为：

(21)

(22)

3.2 不同荷载作用下的挠度解析解

当简支梁任意位置受到集中荷载F作用时，如图5，梁的内力和位移需要分段表达，集中荷载F左、右两边的梁段用下标i和j标注，m、n分别为集中荷载下左、右长度。

图5 集中荷载作用下的简支梁Fig. 5 Simply supported beam under concentrated load

求解微分方程(20)，并考虑u(x)的连续条件和边界条件：

(23)

可得：

(25)

将式(24)、式(25)代入式(18)，即可得到集中荷载作用下简支钢桁腹混凝土组合梁的挠曲线微分方程：

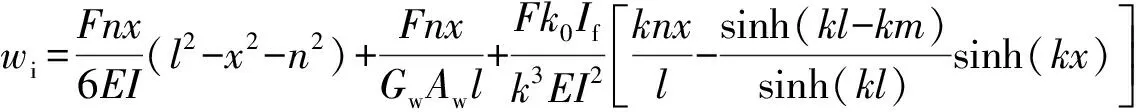
(26)

(27)

(28)

当0≤x≤l/2时，有：

(29)

同理可得简支钢桁腹混凝土组合梁在均布荷载作用下的u(x)及挠度方程w，均布荷载作用下的简支梁如图6。

图6 均布荷载作用下的简支梁Fig. 6 Simply supported beam under uniform load

式(26)、式(27)、式(29)的挠度方程可表达为：

w=w1+w2+w3

(30)

式中：w1为材料力学中按初等梁理论求得的简支钢桁腹混凝土组合梁的弯曲变形产生的竖向挠度；w2为剪切变形产生的竖向挠度；w3为剪力滞效应引起的附加挠度。

4 算例分析

4.1 截面参数

为验证式(26)、式(27)、式(29)的准确性及适用性，利用ABAQUS软件建立简支钢桁腹混凝土组合梁有限元模型，分析其在集中荷载和均布荷载两种不同加载工况下的竖向挠度，具体尺寸和有限元模型如图7。计算跨径l=3.36 m，顶、底板混凝土采用C30，弹性模量为3.0×104MPa,腹杆采用直径为50 mm，壁厚为5 mm的Q345B级钢管，弹性模量为2.06×105MPa，腹杆的水平倾角为60°，直腹杆与斜腹杆的竖向夹角为30°，节点间距为420 mm。加载工况分别为跨中F=100 kN的集中荷载和q=10 kN/m的均布荷载。

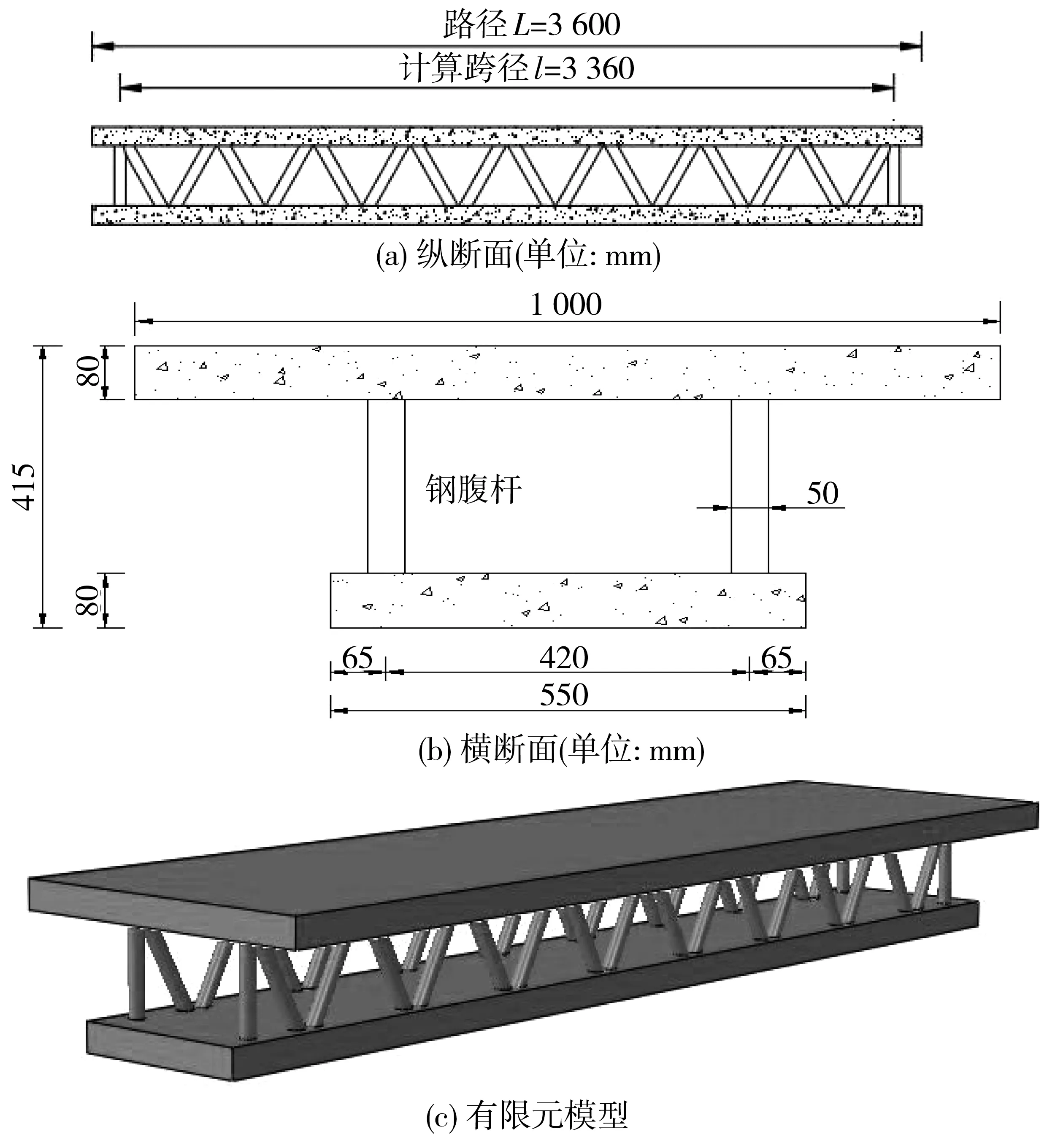
图7 截面尺寸与有限元模型Fig. 7 Sectional size and finite element model

由式(3)可得换算后的等效钢腹板的厚度为1.89 mm，由材料力学知识及式(8)～式(10)求得其截面特征值，如表1。

表1 截面特征值Table 1 Section characteristic value

4.2 集中荷载作用下的简支钢桁腹混凝土组合梁

集中荷载作用下，简支钢桁腹混凝土组合梁的加载形式如图8。集中力F=100 kN，加载点在L/2处，有限元分析的结果如图9。

将截面特征值、荷载和相关参数代入推导的式(26)、式(27)中，并与有限元分析提取出来的挠度值f比较，结果如图10和表2。

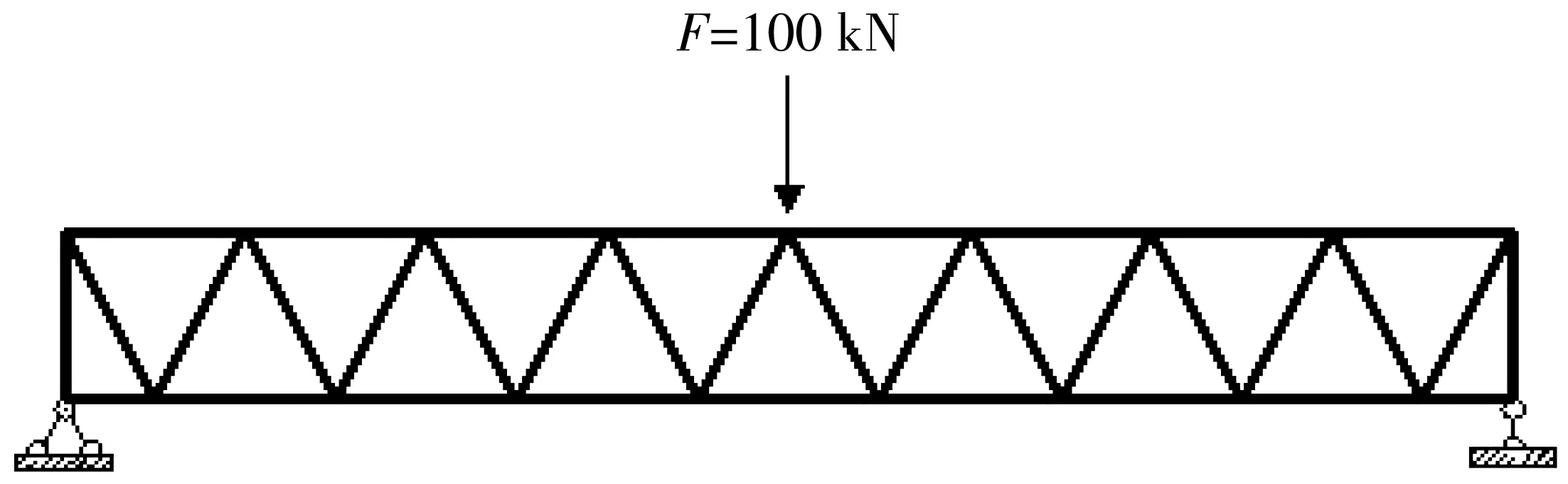
图8 集中荷载作用下的简支钢桁腹混凝土组合梁Fig. 8 Simply supported steel truss web concrete composite beam under concentrated load

图9 集中荷载作用下有限元分析变形Fig. 9 Deformation diagram of finite element analysis under concentrated load

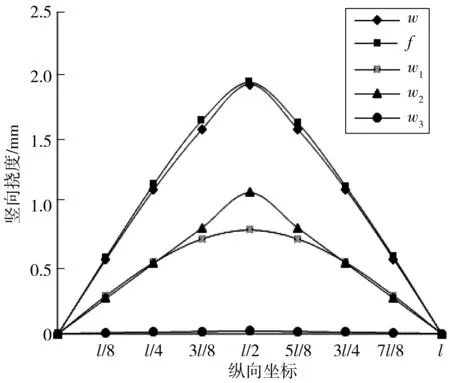
图10 集中荷载作用下梁的竖向挠度曲线Fig. 10 Vertical deflection curve of beam under concentrated load

由图10可知：对于集中加载工况，简支钢桁腹混凝土组合梁的挠度公式计算结果与有限元分析误差较小，沿桥的纵向方向，有限元分析值与理论计算值基本吻合，式(26)、式(27)可靠。越靠近加载点，剪变形产生的挠度与弯曲变形产生的挠度差值越大，剪切变形效应越明显，而剪力滞效应引起的附加挠度对钢桁腹混凝土组合梁的挠度影响较小，几乎可以忽略不计。

表2 集中荷载作用下的挠度对比Table 2 Deflection comparison under concentrated load %

由表2可知：集中荷载作用下挠度有限元分析值与理论分析值误差最大为4.4%，在加载点处的误差仅为1.0%，满足工程中变形计算的精度要求。

4.3 均布荷载作用下的简支钢桁腹混凝土组合梁

均布荷载作用下的简支钢桁腹混凝土组合梁的加载形式如图11。均布力的大小q=10 kN/m,有限元分析的结果如图12。

图11 均布荷载作用下的简支钢桁腹混凝土组合梁Fig. 11 Simply supported steel truss web concrete composite beam under uniform load

图12 均布荷载作用下有限元分析变形Fig. 12 Deformation diagram of finite element analysis under uniform load

将截面特征值、荷载和相关参数代式(29)，并与有限元分析提取的挠度值f比较，结果如图13和表3。

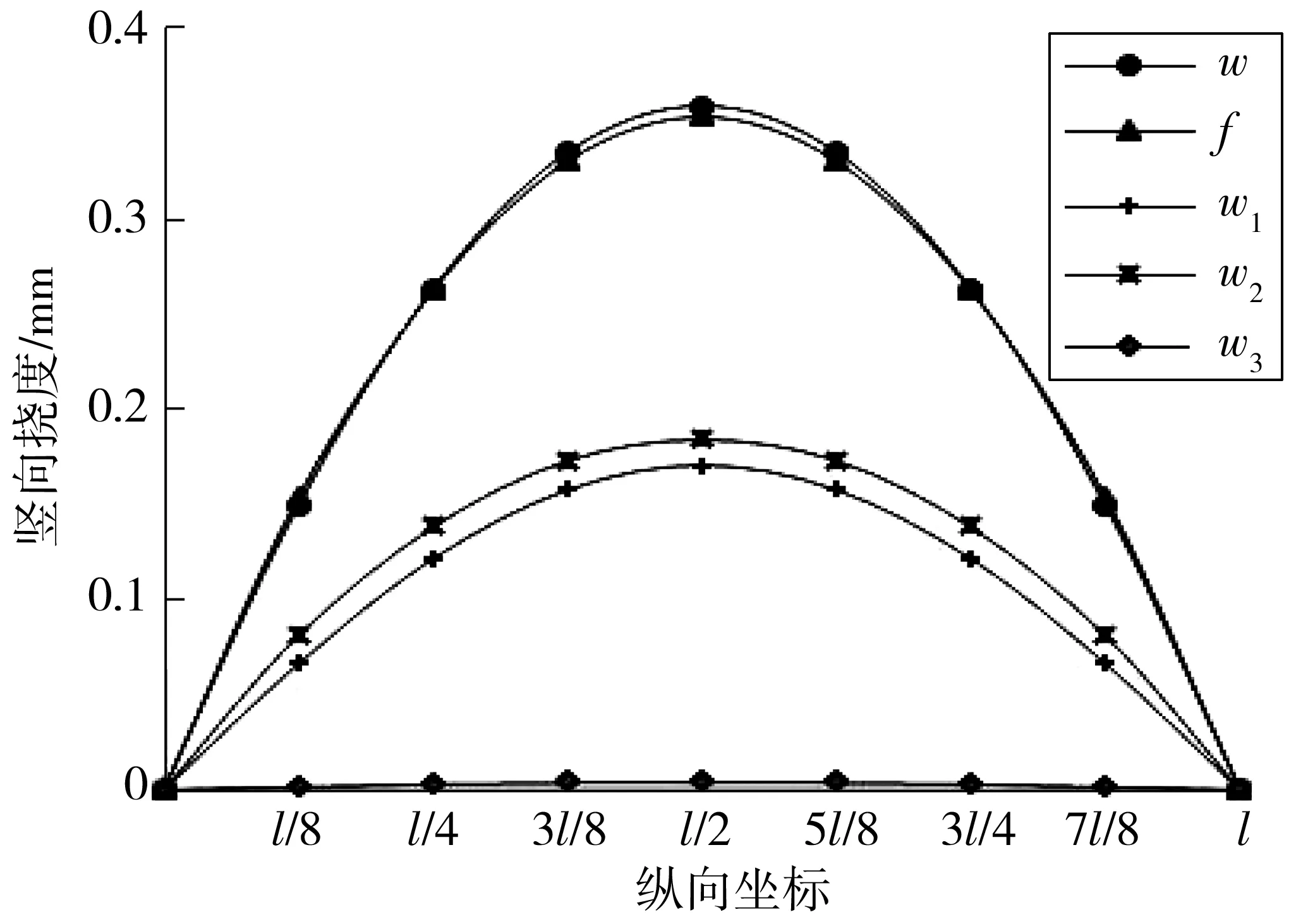
图13 均布荷载作用下梁的竖向挠度曲线Fig. 13 Vertical deflection curve of beam under uniform load

由图13可知：均布荷载作用下，简支钢桁腹混凝土组合梁的挠度公式计算结果与有限元分析误差较小，沿桥的纵向方向，有限元分析挠度曲线与理论分析挠度曲线基本吻合，式(29)可靠。剪切变形对挠度的影响在全跨范围内都高于弯曲变形对挠度的影响，而剪力滞效应的影响较小，几乎可以忽略不计。

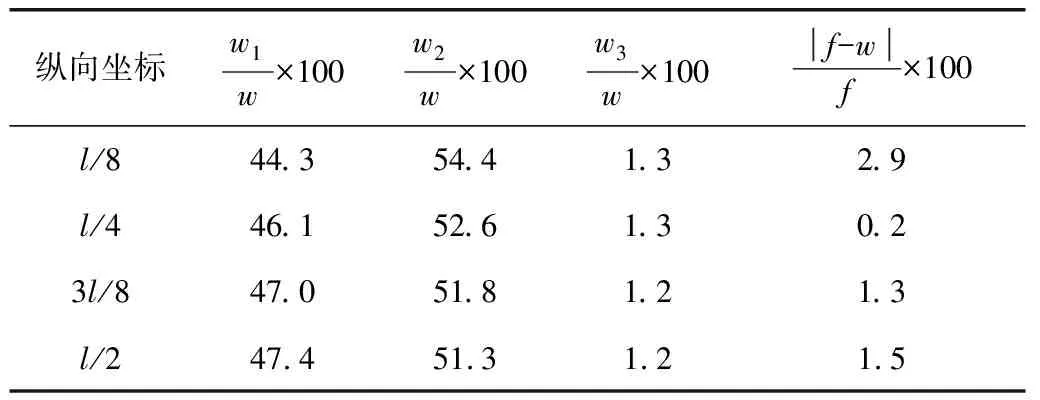
表3 均布荷载作用下的挠度对比Table 3 Deflection comparison under uniform load %

由表3可知：均布荷载作用下挠度有限元分析值与理论分析值误差最大为2.9%，最小仅为0.2%，同样满足工程中挠度计算的精度要求。

对比表2与表3发现：

1) 剪切变形和弯曲变形对钢桁腹混凝土组合梁的挠度影响最大在98%以上，剪力滞效应引起的附加挠度仅为1.2%左右。

2) 集中荷载作用下，在加载点处的剪切变形较为严重;均布荷载作用下，剪切变形对挠度的贡献值在跨径范围内均超过50%。

因此，在进行钢桁腹混凝土组合梁的挠度计算时，剪切变形对挠度的影响必须予以考虑。

5 结 论

考虑钢桁腹混凝土组合梁剪切变形对挠度的影响，利用能量变分法，对钢桁腹混凝土组合梁挠度计算进行分析，得到如下结论：

1) 考虑剪切变形影响得到的钢桁腹混凝土组合梁的挠度值与有限元分析结果吻合较好，在集中荷载和均布荷载两种加载工况下的挠度误差较小，可靠性强。

2) 均布荷载作用下的简支钢桁腹混凝土组合梁，全跨范围内的剪切变形对挠度的影响都大于弯曲变形；集中荷载作用下的简支钢桁腹混凝土组合梁，剪切变形在跨中位置较弯曲变形明显。

3) 在集中荷载和均布荷载两种不同的加载工况下，剪切变形与弯曲变形产生的竖向挠度为钢桁腹混凝土组合梁挠度的主要部分，在98%以上，而剪力滞产生的附加挠度仅为1.2%左右，几乎可以忽略不计。

4) 对于钢桁腹混凝土组合梁这种弱腹式组合梁桥，剪切变形对该类型桥梁的挠度影响必须予以考虑。