基于EEMD和小波阈值的短时交通流预测研究

马莹莹，靳雪振

(华南理工大学 土木与交通学院，广东 广州 510640)

0 引 言

短时交通流预测可为交通控制及交通诱导提供数据支撑，是智能交通领域研究的重点和热点。交通流数据采集过程中易受随机因素影响，导致交通流数据非线性和不确定性增加，预测难度增大。短时交通预测领域现有研究大致可分为参数预测、非参数预测和组合预测等3大类。邱敦国等[1]综合SARIMA模型在历史周期性预测上的优势和RBF模型在空间相关性的预测优势，提出SARIMA-RBF模型，在同时考虑交通流历史周期性和空间相关性情况下，其相较于单个模型具有更好的预测效果；李林超等[2]以交通流纵向时间及横向空间相关性构建时间-空间状态向量，采用网格搜索方法对支持向量回归模型参数进行标定建立预测模型，结果表明，相对于传统支持向量回归模型，考虑交通流时、空间相关关系可提升模型预测精度。

深度学习算法[3]凭借其深层结构特点的优势，开始被应用于短时交通流预测领域，其中包括堆叠自动编码机(SAE)模型、深度置信网路(DBN)模型[4]、长短期记忆网络(LSTM)模型[5]、卷积神经网络(CNN)模型[6]，其中以长短期记忆网络的应用最为广泛。翁小雄等[7]考虑引入交通流数据中的客车占比特征，提高了基于LSTM短时交通流预测模型的预测精度；闫佳庆等[8]通过对路网路段的时空分析, 并引入大型车因素，提高了基于GRU神经网络的交通流速度预测模型的预测准确度。

交通流数据具有随机性和非线性特征，传统的小波分析通过对数据的分解与重构，能够有效的对原始数据进行降噪，但小波去噪的效果会受小波函数的选取以及小波分解尺度大小的影响，从而影响组合预测模型精度。集合经验模态分解(ensemble empirical mode decomposition ，EEMD)可依据数据自身的时间尺度特征进行分解，即将原始数据或信号分解为有限个本征模函数(Intrinsic Mode Function，IMF)。经分解得到的各IMF分量包含原数据不同时间尺度的局部特征信号，在使用时无需设定任何基函数，与建立在先验性的谐波基函数和小波基函数上小波分析算法具有本质差别和特有优势。

综上，笔者提出一种基于EEMD和小波分析的数据分析方法，利用EEMD将原交通流时间序列分解为N个本征模态函数(IMF)和1个趋势项(Res)，并利用小波分析对IMF分量进行降噪处理。在此基础上，提出两类短时短时交通流预测模型构建方法，并分别构建基于长短时记忆网络模型(long short-term memory, LSTM)、序列模型(Sequence to Sequence, Seq2seq)和引入注意力机制序列模型(sequence to sequence with attention，Seq2seq-Attention)的短时交通流预测模型进行对比，对所提两类模型构建方法的有效性及普适性进行检验。

1 EEMD+小波分析组合算法

1.1 集合经验模态分解

为解决经验模态分解(empirical mode decomposition，EMD)在分解原数据时，模态混叠现象缺陷及迭代停止条件缺乏统一标准等问题，文献[8]提出了集合经验模态分解(EEMD)，即通过一种噪声辅助信号处理(NADA)，利用添加均值为0的高斯白噪声进行辅助分析，即EEMD，过程为：

Step 1：将白噪声信号ω(t)加入原始信号x(t)中，得到信号x′(t)：

x′(t)=x(t)+ω(t)

(1)

Step 2：将信号x′(t)进行分解，得到多个本征模态函数Ii(t)(i=1,2,…,N)和1个趋势项r′(t)：

(2)

Step 3：重复Step 1、Step 2，每次加入强度相同、序列不等的白噪声：

(3)

Step 4：利用白噪声频谱的均值为零的特点，将所得IMF分量求均值，得到最终IMF分量Ii(t)：

(4)

1.2 小波分析

对信号进行小波分解后，利用门限阈值对所分解的小波系数进行权重处理，然后对小信号再进行重构，即可达到信号降噪的目的。小波分析的基本思想是使用一簇小波函数来表示或逼近某一信号或函数，其中小波函数是小波分析的关键，是具有震荡性、能够迅速衰减到0的一类函数，即小波函数ψ(t)∈L2(R)，且满足：

(5)

(6)

式中：ψ(t)为基小波函数，其可通过尺度的伸缩和时间轴上的平移构成一簇函数系；ψa,b(t)为子小波；a为尺度因子，反映小波的周期长度；b为平移因子，反映时间上的平移，且有a,b∈R,a≠0。

若ψa,b(t)是由式(6)给出的子小波，对于给定的能量有限信号f(t)=L2(R)，其连续小波变换(continuous wavelet transform，CWT)为：

(7)

交通流时间序列数据属于离散数据可表示为函数f(kΔ)，其中：k表示样本数量，且k=1,2,…,N；Δ表示取样时间间隔，通常为5 min，则式(7)的离散小波变换形式为：

(8)

1.3 EEMD+小波分析组合降噪

EEMD分解得到的前几个本征模态分量，通常集中了原信号中最显著、最重要的信息，分量的频率是从高到底排列的，并且会随着信号的变化而变化。为充分利用EEMD与小波分析两种算法在数据处理方面的各自优势，笔者提出一种EEMD与小波分析组合的数据降噪方法，分为两个步骤：

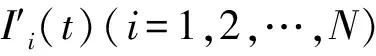
(9)

式中：N为分解所得IMF分量个数，其数量和IMF的定义有关，由极值点以及筛选终止条件来决定，也可在EMD分解中人为设置IMF分量的个数，使其不受终止条件的限制。

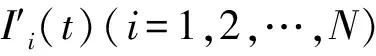
2 基于EEMD+小波分析算法的短时交通流预测模型

在运用EEMD+小波分析算法对数据进行预处理的基础上，提出2类短时交通流组合预测模型构建方法：将经过EEMD+小波分析降噪的IMF分量和残差分量进行重组，并将重组后的数据作为短时交通流预测模型的输入数据，模型输出值为最终预测结果(方法1)；将经EEMD+小波分析降噪的IMF分量和趋势项分别作为短时交通流预测模型的输入数据，对模型输出的各分量预测值进行重组，作为最终预测结果(方法2)。

2.1 方法1

将经过EEMD+小波分析算法降噪后的IMF分量和趋势项进行重组，并将重组后的数据作为短时交通流预测模型的输入数据，以此建立一个基于EEMD+小波分析算法，重构原时间序列数据的短时交通流预测模型，其主要实现步骤如下：

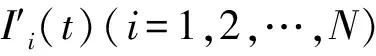
Step 2：将小波分析降噪处理后的本征模态函数I″i(t)和趋势项进行重构，得到重构信号x″(t)：

(10)

Step 3：选取Min-Max标准化方法对数据进行归一化处理，即通过对原始数据的线性变换，使结果落到[0，1]区间；

Step 4：确定LSTM模型、Seq2seq模型、Seq2seq-Attention模型等3个短时交通流预测模型的网络结构及超参数。模型超参数包括网络层数、隐藏层单元数、学习率、迭代次数、激励函数、损失函数、优化函数、批处理数量等；

Step 5：利用训练集数据对建立的短时交通流预测模型进行训练，更新各层连接权值，达到期望误差或最大迭代次数后，停止训练，反归一化输出结果得到最终预测值。

2.2 方法2

将经EEMD+小波分析降噪的IMF分量和趋势项分别作为短时交通流预测模型的输入数据，对模型输出的各分量预测值进行重组，以此建立一个基于EEMD+小波分析算法分量预测组合的短时交通流预测模型，主要实现步骤如下：

Step 1：同方法1中Step 1；

Step 2：选取Min-Max标准化方法对IMF分量和趋势项进行归一化处理，即通过对原始数据的线性变换，使结果落到[0，1]区间；

Step 3：将经小波分析和归一化处理后的I′i(t)和趋势项分别作为单独的数据集输入建立的LSTM、Seq2seq、Seq2seq Attention等短时交通流预测模型；

Step 4：同方法1中Step 4；

Step 5：利用训练数据对短时交通流预测模型进行训练，更新各层连接权值，达到期望误差或最大迭代次数后，停止训练，反归一化输出结果。

Step 6：利用式(10)将模型输出的各分量预测值进行重构，重构后的数据即为最终预测值。

2.3 评价指标

为对所建立的短时交通流预测模型的回归效果进行分析，选取均方根误差(RMSE)、平均绝对百分比误差(MAPE)以及确定系数(R2)来评估模型拟合效果。其中RMSE衡量观测值同真值之间的偏差；MAPE为0%表示完美模型，MAPE大于100%则表示劣质模型；R2也称为拟合优度统计量，越接近1表明回归线与各观测点越接近，回归的拟合程度就越好。计算公式如下：

(11)

(12)

式中：y′={y′1,y′2,…,y′n}为预测值，y={y1,y2,…,yn}为真实值。

3 实例分析

3.1 数据描述

研究数据来自加拿大Whitemud Drive高速公路，它是一条横穿加拿大阿尔伯塔省埃德蒙顿市的市内高速公路，全长28 km，基本限速为80 km/h，数据记录频率为20 s/次，在主干道和闸道上装有地感线圈，用于观测车流量、车速以及车辆密度。

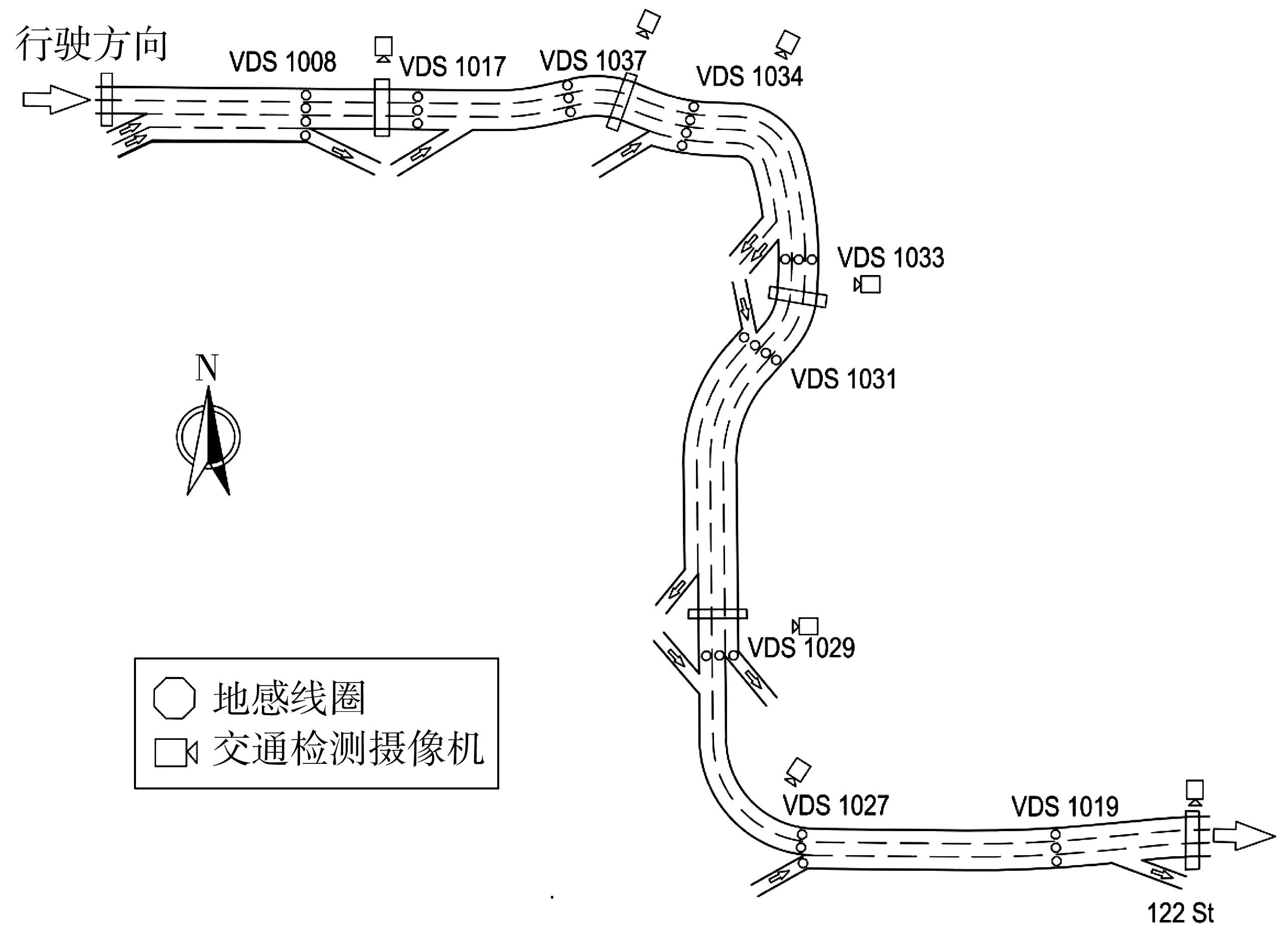
图1 Whitemud Drive高速地感线圈位置分布Fig. 1 Position distribution of Whitemud Drive high-speed ground induction coil

选取该高速东行方向的地磁线圈数据作为研究对象，随机选取VDS1017、VDS1034、VDS1029、VDS1019这 4个检测器数据为研究对象，选取2015年8月8日至28日(剔除周末数据)共15天数据，以5 min时间间隔进行聚合，前14天数据作为模型训练集(共4 032组)，第15天数据作为模型测试集(共288组)。

3.2 EEMD+小波分析算法对原数据降噪

利用EEMD算法对VDS1017检测器处流量数据进行分解。该信号经过EEMD分解得到10个本征模态分量和1个趋势项Res，结果如图2。

由于随机噪声信号在不同时刻的关联性较弱，因而其自相关函数在零点处有最大取值，然后在零点两旁迅速衰减接近于0；而一般信号的自相关函数在0点取得最大值后缓慢振荡，不出现迅速衰减至0的现象。因此，对EEMD分解所得IMF分量进行自相关计算，利用含噪分量自相关函数在零点附近迅速衰减的特点来实现对含噪IMF分量的筛选。将EEMD分解得到的IMF分量进行归一化自相关函数处理，结果如图3。

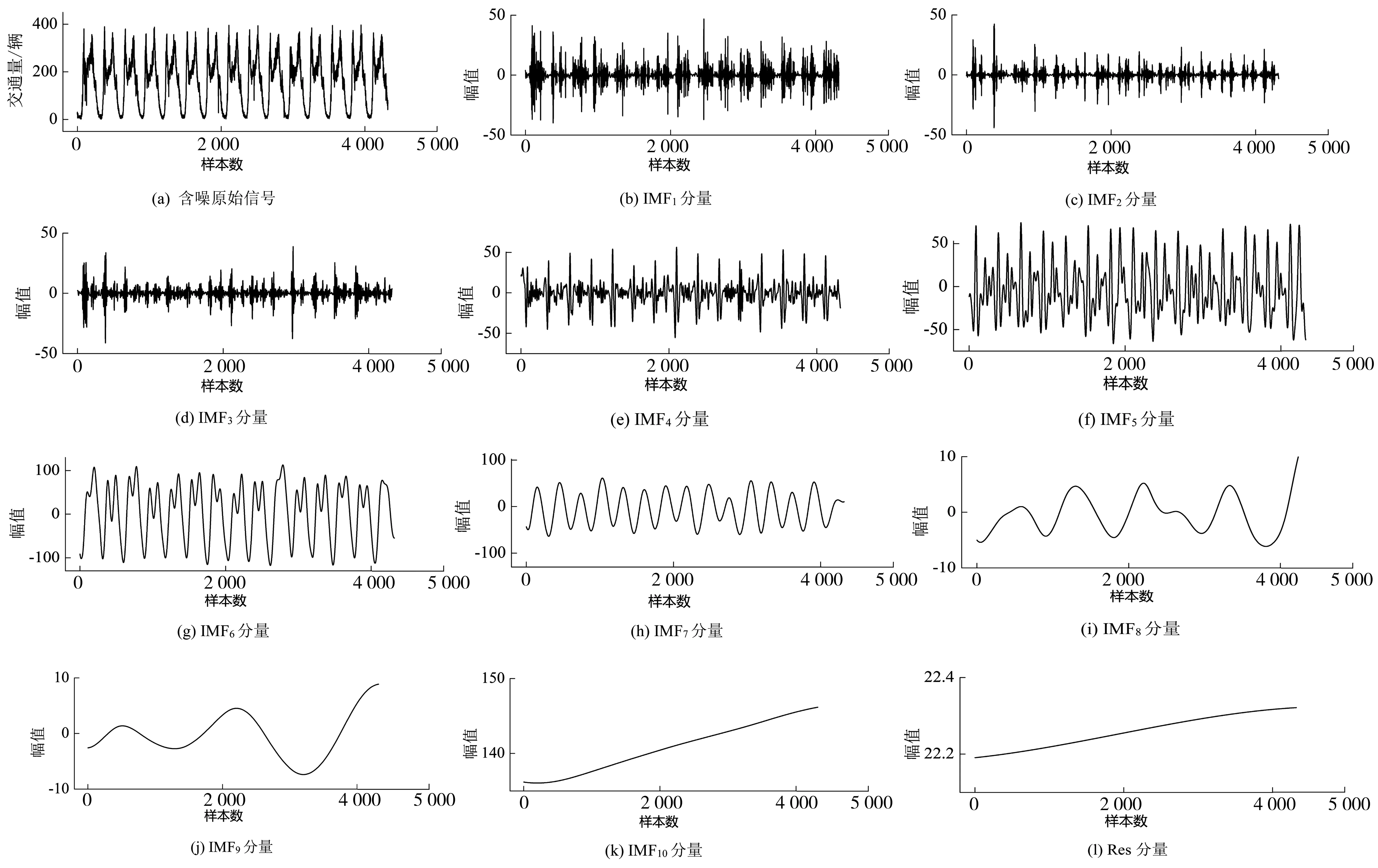
图2 含噪原始信号的EEMD分解结果Fig. 2 EEMD decomposition results of noisy original signal

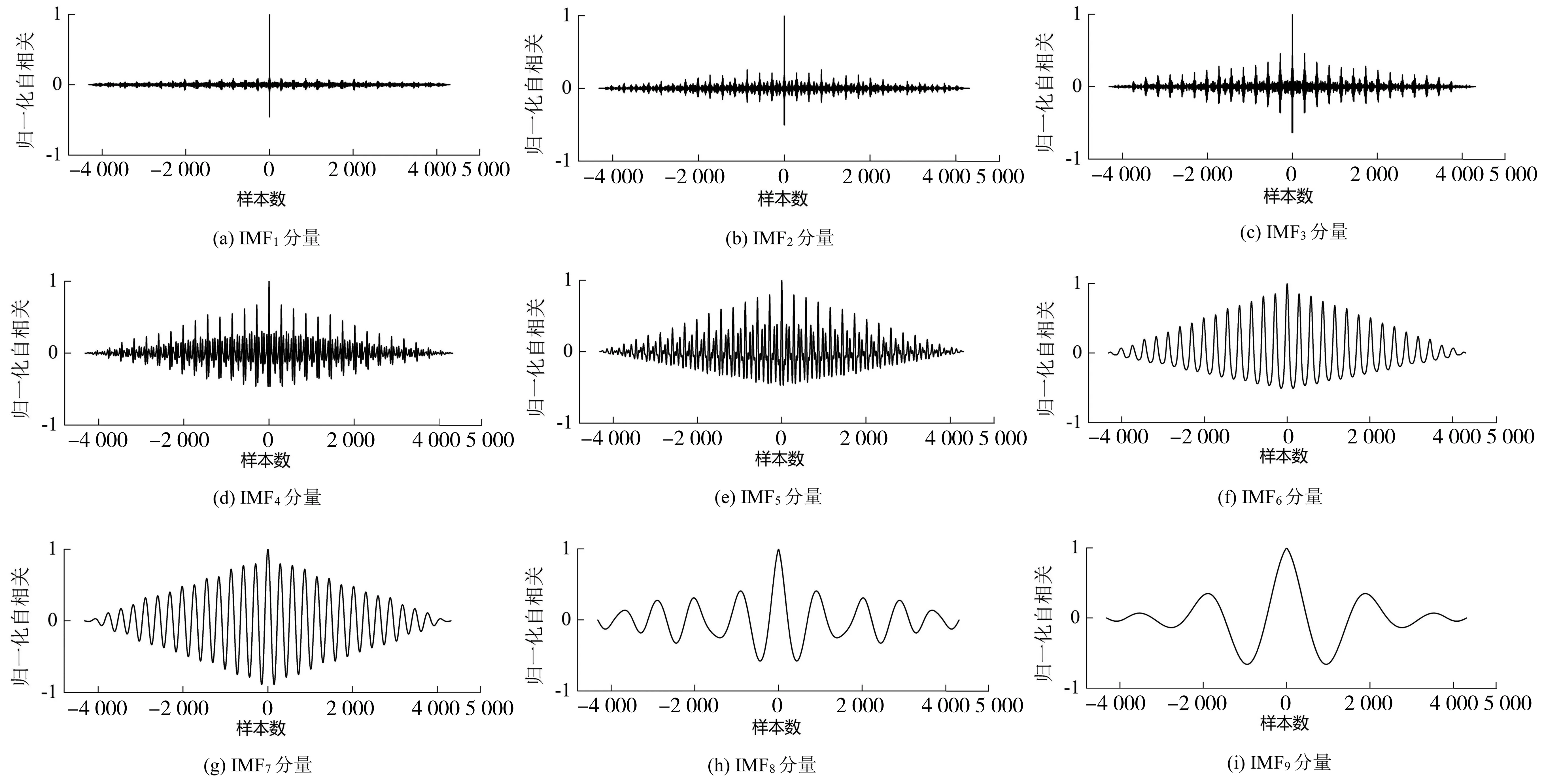
图3 各阶IMF分量的归一化自相关函数Fig. 3 Normalized autocorrelation function of each order of IMF components

根据上述分量筛选原理，IMF1～IMF3在零点处取得最大值后，在零点两旁迅速衰减，表明这3个分量具有明显的含噪特征。因此，选取前3个IMF分量进行小波分析处理，其中小波基函数选取db4小波系，分解层数设定为3，同时保留其他信号主导的IMF分量与余项，小波去噪结果如图4。

由图4可知：经小波降噪处理后，IMF1～IMF3中包含的噪声被有效滤除。

图4 小波降噪效果分析Fig. 4 Analysis of wavelet noise reduction effect

为验证筛选方法的有效性，对IMF4作小波分析处理，观察图像发现降噪后的IMF4与原IMF4分量几乎无变化，可知IMF4分量中几乎不含噪声，进一步表明了筛选方法的有效性。

3.3 预测结果分析

运用VDS1017、VDS1034、VDS1029、VDS1019 这4个检测器处数据，对基于方法1、方法2与LSTM模型、Seq2seq模型、Seq2Seq Attention模型组合构建的短时交通流预测模型的有效性和适应性进行分析，将所提方法1、方法2分别与单一的LSTM模型、Seq2seq模型、Seq2Seq-Attention模型和小波分析-LSTM模型、小波分析-Seq2seq模型和小波分析-Seq2Seq Attention模型的预测性能进行对比实验，结果如图5。

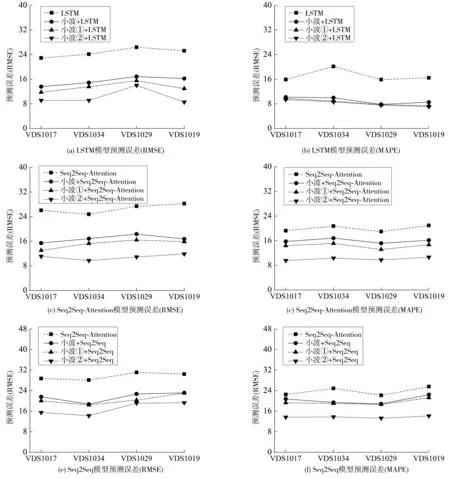
图5 模型误差指标对比Fig. 5 Comparison of model error indicators

对比选取的四个模型的均方根误差、平均绝对百分比误差可知：相较于单一的LSTM模型、Seq2seq模型、Seq2Seq-Attention模型和小波分析-LSTM模型、小波分析-Seq2seq模型和小波分析-Seq2Seq Attention模型，基于方法1、方法2与LSTM模型、Seq2seq模型、Seq2Seq-Attention模型组合构建的预测模型的误差评价指标均明显下降，模型性能最好的为基于方法2的组合预测模型、其次是基于方法1的预测模型，最后分别是基于小波分析的组合预测模型和单一模型。

笔者所提的两类组合预测模型能大幅提高原预测模型的预测性能，方法2对于模型的提升效果最佳，并在LSTM模型、Seq2seq模型、Seq2Seq-Attention模型这3种类型的模型中均得到验证。表明笔者所提出的两类组合预测模型构建方法具有很高的准确度和普适性。

4 结 语

针对交通流数据非线性和不确定性的特点，利用集合经验模态分解(EEMD)和小波分析来去除原交通流时间序列数据中的随机噪声部分，并在此基础上提出的两类短时交通流组合预测模型构建方法。通过借助长短期记忆网络(LSTM)、序列模型(Seq2seq)、引入注意力机制序列模型(Seq2seq-Attention)等短时交通流预测模型进行试验，表明所提两类模型构建方法具有很高的有效性和普适性，通过分别与单一的LSTM、Seq2seq和Seq2Seq-Attention模型以及基于小波分析与LSTM、Seq2seq和Seq2Seq-Attention模型的组合预测模型进行对比实验，表明两类方法均能有效提升初始短时交通流预测模型的预测性能，且方法2对于模型的提升效果更加显著。

笔者试验场景为高速公路断面，未充分考虑道路网络的空间复杂性及其他维度信息，如速度、密度、占有率或天气状况等外部信息，后续研究将结合复杂的交通网络及道路环境构建预测模型，增强预测模型的泛化能力，进一步提高短时交通流预测模型性能，为高速公路信息预测和交通诱导措施制定提供支撑。