谈一道几何例题的变式应用与方法探究

2022-06-24陈结洪

少男少女·教育管理 2022年5期

陈结洪

摘要：通过深挖教材例题的教学功能和引导思考的作用，发现圆的证明与计算在初中阶段的图形与几何中占据重要地位。广州市中考题在探究圆的基本性质的基础上，对四边形与圆进行综合应用和渗透数学思想方法，考查学生对综合知识的掌握程度。文章以人教版九年级数学教材第24章圆周角的例题4，结合各地中考题的变式应用，谈圆背景下的例题变式应用与方法探究。

关键词：教材例题;圆变式应用;方法探究

一、问题提出

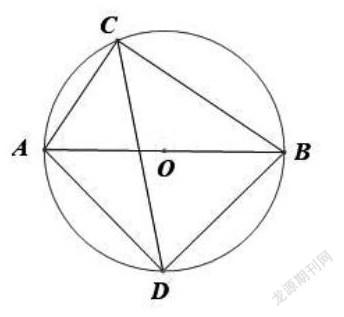
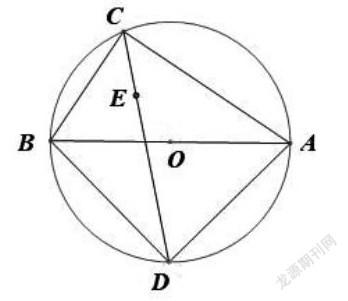
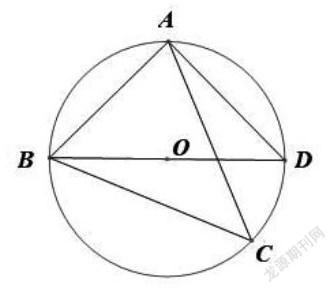
例题呈现：如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于点D，求BC，AD，BD的长。

点评：解答此题需要抓住两个关键。

（1）判断出△ABC和△ABD是直角三角形，以便利用勾股定理;

（2）判断出线段AD=DB，然后将各个线段转化到直角三角形中利用勾股定理解答，注意掌握数形结合思想的应用。

（一）夯实基础，剖析研学内容

本例题是在学生学习圆周角定理知识后，根据学生的知识水平和认知能力，编写的一道既能巩固圆周角定理又能把代数与几何相互运用的基础题。题目虽然是求弦BC，AD，BD的长，但是没有圆的知识，则没有办法把弦AD和BD的关系求出来。题目已知条件是通过∠ACB的平分线得到两个圆周角相等，从而巩固弦、弧、圆心角、圆周角的关系，再利用直径得到相应的直角，得到直角三角形由勾股定理则可求得相应的长度。

（二）层层递进，设置研学问题

例题以圆为背景，强化核心知识点的运用，例如本题中的角平分线的作用是什么？它能让学生得到什么结论？怎样才能把线段和弦建立关系？圆周角和弦是怎样联系在一起的？圆中的直径能为学生搭建怎样的关联？从而找到计算相关的直角三角形，寻找直角三角形的目的是什么？

内化引导。通过例题涵盖的知识点和实际考查的意义，设置一系列的研学问题，逐层递进引导学生进行思考。把问题设置由浅入深，有梯度地引导不同层次的学生，既能全面普及，又能激发学生的学习热情，同时能引导中上生开发思维，呈现螺旋式思维上升，让学生在不断体会相关知识的同时，又能巩固对相关知识点的考查形式，从而达到学以致用的目的。

外围概括。本例题的具体目标是考查学生求相关线段的长度，通过审题分析可以发现，只用到已知的数据是不能求到相应线段的长度。因此，要培养学生要建立起数形结合的思想方法，要有方程的思想意识为突破口进行解题。在思维活动中要有列方程解方程的思想意识，从而再结合题意通过直径找到直角三角形进行勾股定理运算。“数缺形时难直观，形缺数时难入微”，所以，教师在日常的教学中要适当培养学生通过关注知识点，深入研究例题的功能和作用，养成独立思考，独立提炼的习惯。

二、变式应用

（一）探究教材谈变式，深入实践教学

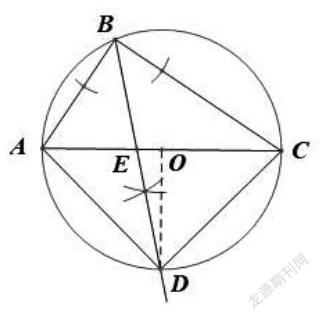
题目呈现：如图，⊙O的直径AB，弦BC为6cm，弦AC为8cm，∠ACB的平分线交⊙O于点D，

（1）求AB，BD的长;

（2）若点E是△ABC的内心，求证：DE=DB.

点评：题目变式源于教材124页总复习的习题，考查的知识点仍然是教材例题弦、弧、圆心角、圆周角的关系的已知条件，只是把直径长改为弦长。

内化引导。通过教学实践过程中发现，大多数的学生都没有证明三角形为直角三角形就使用勾股定理，忽略了该定理使用的前提条件。因此，在课堂教学中，我们要核心培养学生关注解题过程的因果关系，否则很容易会造成丢分。其次就是学生没有意识去证明△ABD为等腰直角三角形。

外围概括。变式中針对第（2）小问若点E是△ABC的内心，是学生解题能力的提升。要求学生在深入理解什么是三角形的内心，它是由什么条件来产生的？它能得到什么样的结论？怎样把内心与角平分线结合使用？设置研学问题上要层层提升，逐步引导学生往内心这个已知条件方向思考。

方法提炼。从学生层面思考，证明两条线段相等，常规的证明方法有哪些？学生普遍都朝着证明全等三角形的方向思考，但在圆背景下的几何图形里，却找不到两对全等的三角形。因此，在引导和思考方向上要寻找其他的方法进行证明，联系证明边相等的角度可以证明该三角形为等腰三角形则可以证毕。

（二）从中考题谈变式，浅出教学细节

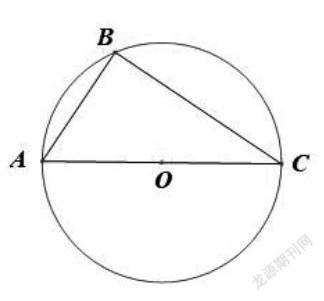
题目呈现：如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°。

（1）利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD（保留作图痕迹，不写作法）;

（2）在（1）所作的图形中，求△ABE与△CDE的面积之比。

点评：本题选自2015年广州市中考数学第23题，主要考查尺规作图、三角形相似的判定与性质、圆的有关性质、特殊三角形三边的关系、解直角三角形，等腰直角三角形的性质、勾股定理等基础知识，考查推理能力、计算能力和转化思想。通过数据可以发现当年的中考情况，为教学带来参考。

内化引导。如右图所示，通过作∠ABC的平分线BD，从形的角度可以发现图形的基本构造与教材例题的背景相仿，得到的知识点弦、弧、圆心角、圆周角的关系也就明确了。圆周角定理、勾股定理的作用也是相当核心的。因此，我们深入理解教材题目和研究题目的知识点，在中考一轮复习，把各个知识点串联在一起，例如相似三角形的判断，同时做到精讲精练是相当有价值的。

方法提炼。层层深入，抓好常规教学，从学困生到中上生，再到尖子生，有针对性地做好脚手架引导，有思维性的深度，又要有技术性的指导，从而提高学生的得分率和教师的教学水平。

例如，本题第（2）求△ABE与△CDE的面积之比，在日常的教学中，让学生体会圆内接四边形相交的对角线容易得到两组相似三角形，然后对照问题直接剖析目标△ABE ∽△CDE，即便不能把证明思路往下写，但找到相关的得分点。再深入研究相似三角形的面积比，如果两个三角形的面积难于逐一计算，可以尝试转化为线段比的平方即可。正如本小问可以转化为线段AB与CD比的平方，那么问题的核心就转化为求线段AB和CD即可。这与教材例题是如出一辙，在例题的基础上深入变式，通过对中考题目和教材例题一系列的深入研究，能不断拓展我们的学习能力和提升自身的教学水平。

三、方法探究

（一）玩转变式，螺旋提升

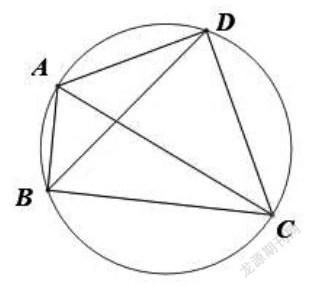
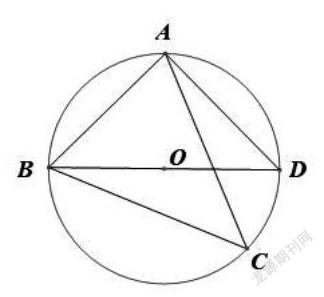
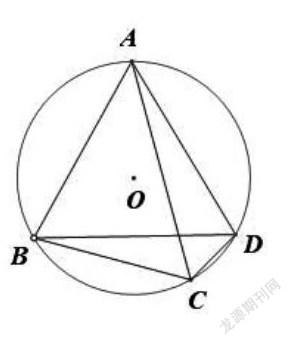
题目呈现：如图，点C为△ABD的外接圆上的一动点（点C不在[ABD]上，且不与点B，D重合），∠ACB=∠ABD=45°

（1）求证：BD是该外接圆的直径;

（2）连结CD，求证：[2]AC=BC+CD;

点评：本题选自2016年广州市中考数学25题，属于典型的中考压轴题，主要考查圆的综合问题，涉及圆周角定理、等腰三角形的性质、全等三角形的性质与判定、勾股定理等知识，综合程度较高，解题的关键就是构造等腰直角三角形。

剖析本题与教材例题的共性分析，首先是背景图与例题极度相似。其次，弦、弧、圆心角、圆周角的关系是解答本题过程的纽带，同时直径是中心桥梁，作为已知条件与隐含条件的一个关键，教材例题是已知条件给出直径，中考题则要证明弦BD是外接圆的直径，让学生体会知识的可逆性。再次，题目把教材当中的角平分线条件改编成含45°这个已知条件，带有共性的特点。

能力提升。中考题源于教材例题背景但又高于例题的难度，是一道相当优秀的压轴题，既考查相关的基础知识，巩固所学知识，又能拓展学生的思维。探究由例题背景知识所产生的变式训练，达到分层考查的目的，有利于选拔性筛选不同层次的生源。第（2）小问与第（3）问又有梯度和共性联系，但又有形式的不同，解决这两小问的方法较多，但在教学上可以适当培养学生一题多解的同时，可以训练最优解法，让学生节省大量的考试时间，达到效率最大化。

（二）分解变式，由浅入深

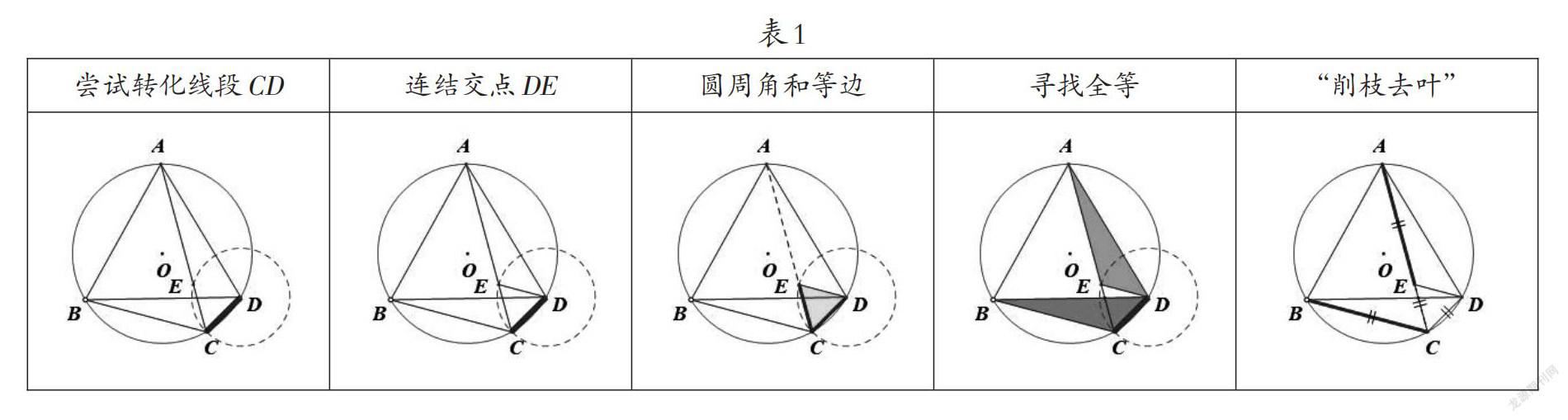
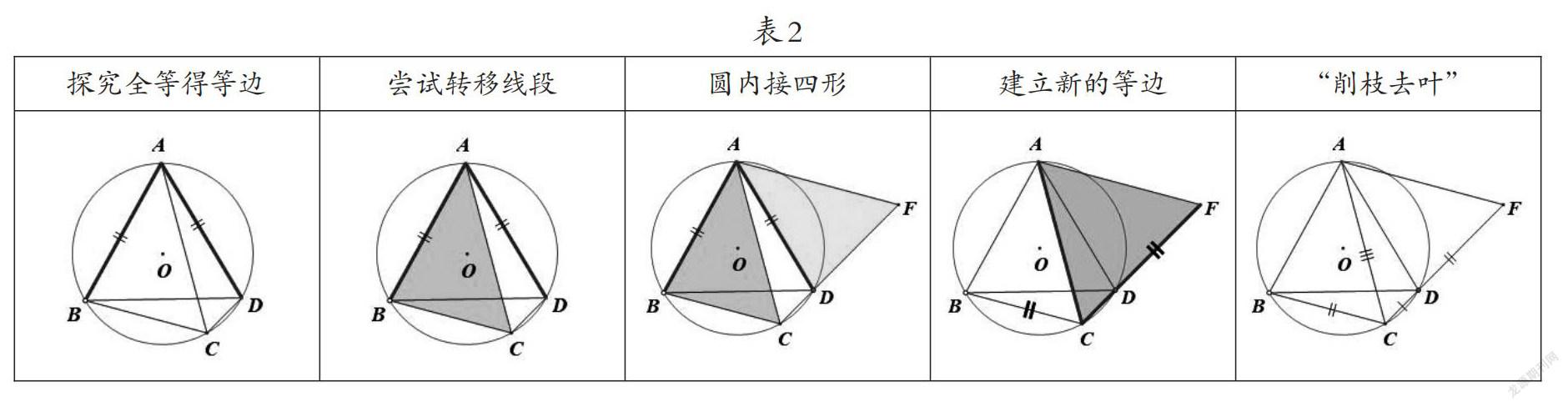
如图，已知△ABD为等边三角形，点C为圆周上的动点，则线段CA，CD，CB满足怎样的数量关系，请说明过程。

点评：含60°的三角形外接圆周上的动点，探究由动点所在的三条线段的数量关系。

研学问题：（1）观察线段CA，CD，CB位置关系呈现怎样的分布形式？（2）怎样处理零散的线段关系？（3）目前已掌握哪些方法可以迁移应用到本问题中？（4）等边三角形能得到什么结论？（5）圆的背景能带来哪些中间的桥梁关系？（6）能否联想其他相关的知识和方法突破本问题？

研学思路：（1）尝试把零散的线段迁移到一个特殊的三角形中理解？（2）能否构建相关全等的三角形来探究相关的线段关系？（3）借助哪些隐含条件进行破题？

截长法探究生成（见表1）。

旋转法生成再探（见表2）。

（三）回归题意，迁移应用

如图，点C为△ABD的外接圆上的一动点（点C不在[ABD]上，且不与点B，D重合），∠ACB=∠ABD=45°，连结CD，求证：[2]AC=BC+CD。

點评：通过引导学生深入思考例题的核心思路，观察对比分解变式题可以得到，题目由等边三角形转化为等腰直角三角形，培养学生对符号感和图形感产生变化作出判断，联系问题的结论中带有[2]。因此，联想等腰直角三角形三边的数量关系1∶1∶[2]，便能快速定位到常规的截长法和旋转的方法来突破解题。

（四）课外知识拓展，探究深层知识联系

托勒密定理认为圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。