基于粒子分解的SPH并行算法研究与应用*

2022-06-23许晓阳王斯棋

计算机工程与科学 2022年6期

许晓阳，王斯棋

(西安科技大学计算机科学与技术学院，陕西西安 710054)

1 引言

自由表面流现象广泛存在于自然界和工业生产中，如注塑成型、水利工程等。处于流动过程的自由面形状复杂，且在演变中可能产生水花四溅、靠近边界处水流猛烈变形、反弹以及与下方水体交融等多种复杂物理现象，是一个强非线性复杂问题。因此，高效、准确地模拟这一流动过程具有重要的理论价值和实用意义。基于传统网格的数值方法如有限差分、有限元法等在解决此类强非线性自由表面流问题时，需要运用额外界面追踪技术，实施过程复杂。

光滑粒子流体动力学SPH(Smoothed Particle Hydrodynamics)方法是一种拉格朗日型无网格方法，适用于模拟自由表面流动。此方法是由Lucy[1]和Gingold等人[2]在1977年首次提出的。与基于网格的数值方法相比，SPH方法完全独立于网格，且具有Lagrangian特性和质点特性、自适应特性等优点，因此非常适合大变形、自由表面流动等复杂界面问题的数值模拟。1994年，Monaghan[3]首次将SPH方法应用于自由面的不可压缩建模，基于可压缩假设构建了一个计算简单的不可压缩流体模型。近年来，SPH方法又被成功用于求解不可压缩流[4,5]、多相流[6,7]、传热[8,9]和粘弹性流[10,11]等问题。值得注意的是，相比于网格类方法，SPH方法在计算过程中计算量大、耗时长，因此有必要对SPH程序进行并行化处理。目前，王裴等人[12]采用固定空间区域方法实现了三维微喷射和斜侵彻的并行SPH模拟。Cherfils等人[13]设计了基于区域分解的SPH并行算法，并对二维水柱倒塌过程中的并行性能进行了研究与分析。吴建松等人[14]借助GPU并行加速技术，应用SPH方法对复杂阶梯流问题进行了数值模拟。范小康等人[15]利用基于可伸缩矢量扩展SVE(Scalable Vector Extension)的单指令多数据SIMD(Single Instruction Multiple Data)结构向量优化方法对SPH数量级并行进行了探索，获得了明显加速效果。梁岚博等人[16]在CUDA软硬件平台上，建立了SPH-GPU并行加速二维气沙两相耦合模型，结果表明该方法能够进一步应用在风沙流数值模拟中。

本文基于消息传递接口MPI(Message Passing Interface)并行程序设计平台，以C++语言作为算法实现的编程语言，设计了基于粒子分解的SPH并行算法。该算法将所有粒子平均分配到各个进程进行计算，每个时间步通信仅调用一次发送、接收和广播函数，因此易于实现且可扩展性较好。应用该并行算法对二维溃坝流和三维液滴冲击液膜问题进行了模拟，分析了进程数、粒子数与并行效率、加速比之间的关系。当粒子数大于百万时，最大加速比可达30以上，为进行三维大规模问题的数值模拟提供了一种高效的计算工具。

2 数学模型与方法

2.1 控制方程

在Lagrangian坐标系下，三维等温、牛顿黏性流体的控制方程组如式(1)和式(2)所示:

(1)

(2)

其中，ρ、v和p分别表示流体密度、速度和压力，t表示时间，η表示流体粘度，g表示重力，D/Dt表示物质导数，其定义如式(3)所示:

(3)

为封闭控制方程式(1)和式(2)，通常将不可压缩流体视为弱可压缩流体，即用状态方程将流体密度的变化范围控制在1%以内，以保证流体流动行为完全接近不可压缩流。本文使用的状态方程如式(4)所示[3]：

(4)

其中，γ=7是一个常数；ρ0表示参照密度，其值为1 000 kg/m3；c表示声速，通常取为流体最大速度的10倍。

2.2 光滑粒子流体动力学(SPH)方法

2.2.1 控制方程的离散

在SPH方法中，函数f(x)在计算域Ω内的积分表达式可写为式(5)所示:

(5)

其中，x表示位置矢量，W(·)表示核函数，h表示核函数影响域的光滑长度。本文核函数采用分段三次样条函数，此时影响域半径为2h。

对计算域Ω内第i个粒子的位置矢量，将式(5)转化为核函数支持域内粒子叠加求和的离散化形式,如式(6)所示:

(6)

其中，N表示粒子总数,mj表示第j个粒子的质量；Wij=W(|xij|,h);xij=xi-xj，|xij|表示第i个粒子和第j个粒子之间的距离。同理求得，函数空间导数在粒子i处的粒子近似式如式(7)所示:

(7)

对函数空间导数进行适当的数学处理，利用式(7)可推导出不同的粒子近似式，进而用于控制方程式(1)和式(2)的离散。本文选用的离散形式如式(8)和式(9)[17]所示：

(8)

(9)

其中，vij=vi-vj;ηi和ηj分别表示第i个粒子和第j个粒子的粘度;pi和pj分别表示第i个粒子和第j个粒子的压力;ρi和ρj分别表示第i个粒子和第j个粒子的流体密度;φ=0.01h用于防止粒子相互靠近时产生的数值振荡。

2.2.2 边界处理

边界处理直接影响模拟的效率和稳定性，对于SPH计算至关重要。本文在前期工作[18,19]基础上，提出一种由壁面粒子和边界外虚粒子组成的加强型边界处理方法。

首先，在固壁边界上布置一层壁面粒子，且粒子间距与流体粒子初始间距δ0相等。与Monaghan[3]的边界方法不同，本文壁面粒子不通过施加排斥力以防御流体粒子穿透固壁。与文献[20]和文献[21]的方法类似，壁面粒子参与到流体控制方程的求解中。在计算过程中，壁面粒子的密度和位置不发生变化，压力通过其支持域内流体粒子压力的正则化插值计算得到，如式(10)所示：

(10)

其中，i表示壁面粒子，j表示与壁面粒子i相邻的流体粒子。

其次，在固壁边界外布置几层虚粒子，以弥补壁面粒子的不足。虚粒子与流体粒子初始间距δ0相等，密度和位置在计算过程中保持不变。但与文献[20]和文献[21]的方法不同，虚粒子的速度和压力不再通过构造流体内部伪粒子进行插值计算得到。本文中，每个虚粒子均有唯一的壁面粒子与之相连接。图1展示了虚粒子与壁面粒子的连接关系。为符合无滑移边界条件，壁面粒子和虚粒子的速度均设置为零。虚粒子压力设置与相连接固壁粒子的压力相同。

相比于文献[20]和文献[21]的方法，本文的边界处理将不再需要构造流体区域靠近固壁边界处的伪粒子，从而避免了应用式(10)对伪粒子进行正则化插值的繁琐操作，因此可以缩短三维模拟的计算时间。

2.2.3 时间积分

由于蛙跳法具有二阶精度，且对于三维问题的存储需求量小、计算效率高，因此本文选用该方法对SPH离散方程式(8)和式(9)进行时间积分。关于蛙跳法的时间步推进公式可参阅文献[17]。

3 基于粒子分解的SPH并行算法

3.1 算法流程

本文基于MPI并行程序设计平台，以C++语言作为算法实现的编程语言，设计了一套基于粒子分解的SPH并行算法。

该并行算法的基本思想是把相邻粒子间相互作用力的计算，根据各处理器计算能力各自分配一定数量的粒子，进行每一时间步的通信和并行计算。首先，输入初始粒子信息和计算所需的其它数据，将所有粒子平均分配到各个进程：设总粒子数为N，总进程数为P，进程数标记为Z(0≤Z≤P-1)，先计算N/P和N%P，若Z>N%P，则分配给进程Z的粒子起止编号分别为Z×(N/P)+N%P和(Z+1)×(N/P)+N%P-1；否则，分配给进程Z的粒子起止编号分别为Z×(N/P+1)和(Z+1)×(N/P)+Z。其次，对流体控制方程进行并行求解。计算过程中，每一时间步通信仅调用一次发送、接收和广播函数，因此编程易于实现，且可扩展性较好。该并行算法的另一特点是每个进程在每一时间步内均负责维护固定的某一部分粒子，并不考虑粒子实际所处物理空间，因此各进程间的负载平衡易于保证。数值算例表明，该并行算法可显著提升SPH方法模拟三维复杂流动问题的计算能力，对其他如耗散粒子动力学、分子动力学程序并行也可提供有价值的参考。

图2展示了该并行算法的流程。

3.2 评价并行算法的参数

加速比和并行效率是衡量并行算法性能的2个关键参数。

加速比Sn是指同一任务串行运行时间T1与并行运行时间Tn之比，其中n表示所用总进程数。并行效率En是指并行加速比与总进程数之比。En一般小于或等于1，越接近1说明并行加速效率越高。

4 并行计算模型验证

4.1 有效性验证

为了验证基于粒子分解的SPH并行算法模拟自由表面流问题的有效性，对二维溃坝问题进行数值模拟。图3给出了二维溃坝初始状态模型示意图，其几何尺寸与文献[13]的保持一致，即溃坝水体高度H=1 m,长度L=2 m，水槽宽度d=5.366 m,m为水槽高度。流体密度ρ=1 000 kg·m-3，粘度η=10-3Pa·s，重力加速度g=9.81 m·s-2，所用流体粒子数NF=5 000，时间步长Δt=1.0×10-4s。

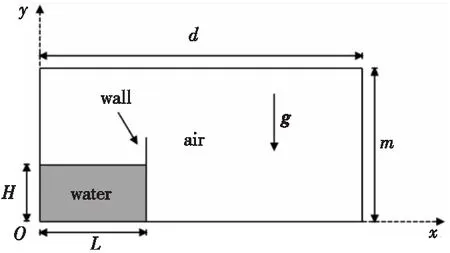
Figure 3 Schematic diagram of 2D dam-break model 图3 二维溃坝模型示意图

Figure 4 SPH particle distribution of dam-break flow at two different times图4 溃坝流在2个不同时刻的粒子分布图

Figure 5 Front position of dam-break flowtime history varying varying with time图5 溃坝流前沿位置随时间的变化图

表1给出了该算例使用不同进程数运行4万个时间步的并行结果。从表1可以看出，当使用2个或4个进程时，可以获得较好的加速比和并行效率，但当所使用的进程数目增加到8个时，加速比和并行效率出现了一定程度的下降。这是由于模拟所用粒子数较少，当所用进程数增加时，分配给每个进程的粒子数相应减少，这造成需要通信的数据占总数据的比例增大，通信量增加，因此加速比和效率出现了下降。

Table 1 Parallel performance analysis of dam-break flow

另外，为进一步分析计算规模增大时的并行性能，图6分别展示了溃坝流在粒子数NF=5000和NF=20000 时的并行效率。可以看出，当所用流体粒子数增加到NF=20000时，使用8个进程时的并行效率较NF=5000时有明显提高，且在85%以上。因此依据等效率可扩展性度量法[22],本文SPH并行算法具有良好的扩展性。

Figure 6 Parallel efficiency of dam-break flow at different computation scales图6 溃坝流在不同计算规模时的并行效率

4.2 三维液滴冲击液膜问题

接下来，本文对三维液滴冲击液膜问题进行SPH并行模拟，其计算模型如图7所示。其中，液滴和液膜采用相同的液体，密度ρ=1200 kg·m-3，粘度η=0.022 Pa·s。液滴直径D=0.0042 m，液滴冲击速度V=5.09 m·s-1。液膜长度和宽度分别为Lx=Ly=5D，液膜厚度H′=0.5D。粒子之间初始间距设置为δ0=0.000105 m，所用粒子总数设置为N=1071521，其中流体粒子总数设置为825 421，边界粒子总数设置为58 801，固壁外虚粒子总数设置为187 299。时间步长Δt=5.0×10-7s，以保证数值稳定性。

Figure 7 Calculation model of 3D droplet impacting liquid film图7 三维液滴冲击液膜的计算模型

图8给出了三维液滴冲击液膜问题在4个不同时刻的SPH结果。可以看出，在t=0.25 ms时，液滴以一定初始速度冲击静止的液膜，液滴部分粒子和受冲击液膜部分粒子相互融合，跃出了液膜表面，形成了薄片射流。在t=0.50 ms时，更多液滴粒子持续冲击液膜，液膜沿着固体壁面向四周逐渐扩展和运动，而薄片射流也持续向上运动，形成了较明显的“皇冠”状水花。在t=1.00 ms时，由于惯性力的作用液滴继续向下运动，最终完全与液膜融合在一起，而部分从“皇冠”状水花边缘脱落的粒子形成小液滴，最终产生水花飞溅现象。很明显，本文SPH并行算法能够形象逼真地捕捉液滴冲击液膜发生的“皇冠”状水花、水花飞溅等多种复杂物理变化。

Figure 8 SPH simulation of 3D droplet impacting liquid film图8 三维液滴冲击液膜的SPH模拟

表2进一步比较了在不同进程数情况下，液滴冲击液膜问题运行一个时间步长消耗的计算时间和并行加速比。可以看出，对于粒子数大于百万的本算例，使用串行程序(进程数为1)所消耗的运行时间为180.9 s，而使用64个进程时计算时间缩减到5.82 s，此时最大加速比可达30以上。这说明，本文基于粒子分解的SPH并行算法能显著减少模拟所用时间，有利于进行三维大规模计算问题的数值模拟。