基于编译时插桩的浮点异常检测方法*

2022-06-23郭思雨

计算机工程与科学 2022年6期

郭思雨，王磊

(中原工学院前沿信息技术研究院，河南郑州 450007)

1 引言

目前，浮点计算被广泛应用于各个领域,现有的计算机硬件设计及IEEE-754[1]标准，决定了浮点数是实数的有限精度编码[2]，不能精确表示出实数，在进行浮点计算时，可能会导致不精确或者异常的结果。由于浮点数转整数出现的整数溢出异常，欧洲Ariane 5火箭在1996年发射时出现了严重的升空自爆现象[3]，造成了巨额的经济损失。因此，提前发现和规避，是目前解决浮点计算异常问题的关键。

能够对异常处理起到指导作用的异常检测方面的研究也在蓬勃发展。当前的测试研究可以分为2类：(1)对浮点异常的研究。文献[2]提出了利用值-范围分析来加速浮点异常检测的符号执行；文献[4]提出的Ariadne，使用实数算法对变换后的程序进行符号执行，以发现可能到达或触发异常的候选实数输入集；文献[5]提出的FPChecker(Floating-Point Checker)，使用Clang/LLVM(Low Level Virtual Machine)编译器检测GPU内核并在运行时检测异常。这类方法多基于符号执行方法，符号执行是一种经典的程序分析技术，它使用符号输入来探索可行的程序路径，但是使用符号执行技术检测浮点异常的代价是昂贵的。(2)对整数溢出的研究。文献[6]基于动态检测技术，通过检测所有可能产生溢出的操作实现了RICH(Run-time Integer CHecking)工具[6];卢锡城等人[7]提出了一种二进制高危整数溢出错误的全自动测试方法DAIDT(Dynamic Automatic Integer-overflow Detection and Testing)；Brick[8]能够检测和定位真实软件中的大部分基于整数的漏洞，并具有较低的误报率；文献[9]基于静态区间分析，提出了利用future bounds对变量进行处理的整数溢出分析算法。

综上所述，现有的方法不是针对浮点数学函数而设计的，其研究重点集中在整数溢出错误，而浮点函数的运算降低了整数溢出存在的可能性。在申威1621平台上也没有专门针对浮点数学函数的异常检测方法，并且目前的研究中对于检测结果的全面性没有进行相关的评估。鉴于此，面向基于汇编实现的浮点数学函数[10]，本文提出了一种针对浮点数学函数的异常检测方法。该检测方法对浮点异常类型进行分类后，在编译函数源码时进行插桩。该方法能自动检测异常、用生成的测试用例对函数进行全面检测的同时记录了代码覆盖率。

2 基础概念

2.1 概念介绍

浮点环境由数据结构和运算组成，并通过硬件、系统软件和软件库提供给程序员，实现了IEEE-754标准。浮点异常(即异常)是指在浮点算术运算中出现的异常，即IEEE-754标准中定义的5种类型的浮点异常:无效操作、被零除、上溢、下溢和不精确异常。浮点函数是指申威高性能基础数学函数库中的浮点数学函数，包括三角函数、指数函数、对数函数和双曲函数等初等函数。代码覆盖率描述了测试数据作为输入时函数的运行情况，通过代码覆盖率可以对该检测过程进行评价。

本文提出的浮点异常检测方法是指在测试阶段对函数程序进行必要的插桩修改，对其内部的运算指令进行异常检测。

2.2 浮点控制寄存器FPCR

浮点控制寄存器FPCR(Floating-Point Control Register)包含浮点异常的状态、浮点舍入模式、浮点异常自陷控制和特殊数据的控制等。浮点控制寄存器FPCR有64位，其中[59:58]位是动态舍入模式位；[57:52]位记录浮点运算指令产生的6种算术异常，也记录浮点SIMD(Single Instruction Multiple Data)运算指令中第0个元素进行运算产生的6种算术异常；[40:36]位、[24:20]位和[8:4]位分别表示浮点SIMD运算指令中第1、第2和第3元素进行运算产生的5种算术异常，由于本文所涉及到的函数为标量函数，所以这些位暂时作为保留位；[63]位是算术异常的总标志位，指示是否存在异常。该寄存器通过浮点指令WFPCR和RFPCR进行访问。

3 检测方法

3.1 异常检测分类

申威1621处理器支持IEEE-754标准定义的5种浮点算术异常，本文研究的浮点数学函数主要包括一系列初等函数[11]，如三角函数、指数函数和对数函数等。本节对浮点算术异常进行相应分类检测，由于产生上溢异常只可能是使浮点数增大的运算或操作，产生下溢异常只可能是使浮点数减小的运算或操作，因此，通过对faddd、fmuld等指令的检测判断是否产生上溢，通过对fsubd、fdivd等指令的检测判断是否产生下溢(其中还需对fdivd指令进行被零除异常的检测)，通过对输入参数的检测判断是否触发无效操作异常。如果舍入后的结果与舍入前的真值不一致，或舍入时产生了上溢而申威1621处理器实现中无上溢自陷，则产生非精确结果(Inexact Result)异常。由于不精确经常发生[4,12]，并且通常是有限精度不可避免的结果，例如，当1.0除以3.0时，会出现不精确的异常，因为比率1/3不能精确表示为浮点数，因此暂不针对不精确异常进行分析。通过以上3种分类对浮点计算异常进行具体检测。下面针对这3种分类进行详细说明：

(1) 无效操作异常检测。

若当前操作的一个操作数为非有限数或对要执行的操作而言是非法的(浮点比较指令的操作数为无穷大时不产生自陷)，或用户输入的参数不满足参数域的范围或输入参数类型不匹配(如将双精度数传给单精度函数)等操作，将会产生无效操作异常。由于无效操作异常产生在用户输入参数阶段，因此可在进入函数正常运算前对用户的输入进行检查，避免浮点数的特殊数参与到浮点运算中引发浮点算术异常，影响浮点函数的可靠性。浮点数的特殊数包括SNaN(Signaling Not a Number)、QNaN(Quiet Not a Number)、Infinity和Denormal等无法正常处理的数据。SNaN一般用于标记未初始化的值，QNaN一般表示未定义的算术运算结果。

在进入函数计算之前，对函数的定义域及输入参数进行对比检测，判断参数是否符合函数定义域，判断是否产生无效操作异常和非规格化数异常。检测输入参数是否为特殊数SNaN和QNaN的源码为：

1. fcmpeq $f16,$f16,$f14

2. fbeq $f14,L$9

3.L$9:

4. faddd $f16,$f16,$f0

5. ret

非数NaN(Not a Number)是计算机科学中一类数值数据类型的值，表示未定义或不可表示的值，常在浮点数运算中使用。因为NaN是一个范围，而不能代表一个确定的值，因此利用NaN！=NaN对输入参数$f16进行判断，如果$f16！=$f16，则该输入参数为非数。其它特殊数可以通过参数定义域范围检测，在函数开始运算之前，把函数定义域放入数据表内。判断输入参数是否在函数定义域内，若在，则继续参与运算；若不在，则直接返回，并报出无效操作异常。

(2)上溢异常检测。

上溢异常是在舍入过程中产生的，当舍入结果的幅值(绝对值)超过目标格式的最大有限值时即产生上溢异常。标量浮点运算指令或SIMD浮点运算指令中的第0个元素进行浮点算术运算或转换操作的结果产生上溢时，FPCR寄存器的第54位置1。只有可以使浮点数增大的浮点运算指令才可能会导致上溢异常的出现，因此针对申威1621处理器中的相关运算指令进行检测，如faddd、fmuld和fmad等浮点运算指令。

根据浮点控制寄存器FPCR对应的上溢异常位进行检测，具体内容如下所示：

①检测前的源码：

…

1. faddd $f16,$f1,$f10

…

②插入检测代码后的源码：

…

1. rfpcr $f8

2. fimovd $f8,$1

3. faddd $f16,$f1,$f10//需要检测的操作

4. rfpcr $f9

5. fimovd $f9,$2

6. sll $1,9,$1

7. srl $1,63,$1//取出FPCR对应上溢异常位

8. sll $2,9,$2

9. srl $2,63,$2

10. cmpeq $1,$2,$3/*判断对比上溢异常位是否发生变化*/

11. beq $3,L$1/*如果触发上溢异常，则跳转至L$1分支，记录该异常*/

12.L$1:

13. call detection//调用该函数记录异常具体信息

…

其中，faddd为浮点加运算；rfpcr为读取当前浮点控制寄存器FPCR的值；fimovd为双精度浮点数传送到整数；cmpeq是等于比较。

以上代码，具体含义为：在源码编译时，检测函数中是否有faddd或fmuld等汇编指令。若有，则将以上内容放置到该指令前后，对比判断是否产生上溢异常。若产生异常，则调用detection函数，记录异常的具体信息，如输入参数、异常类型等信息；若不产生异常，则继续执行其余代码。

(3) 下溢及被零除异常检测。

下溢异常是在舍入过程中产生的，当舍入结果的幅值(绝对值)小于目标格式的最小有限值时即产生下溢异常。标量浮点运算指令或SIMD浮点运算指令中的第0个元素进行浮点算术运算或转换操作的结果产生下溢时，FPCR寄存器的第55位置1。只有可以使浮点数减小的浮点运算指令可能会导致下溢异常的出现，因此针对申威1621处理器中的相关运算指令进行检测，如fsubd、fdivd等浮点运算指令。

被零除异常为当除数为0 ，而被除数为有限数时触发的异常，也泛指有限数运算导致无穷结果的异常，例如4.0/0.0，log(0.0)等。在浮点数学函数实际运算过程中，一般只被除法指令FDIVS/FDIVD触发。被零除异常的检测可以在检测到除法指令时，若被除数是一个不会引起无效操作异常的数据，则对除数进行判断，若除数为0，则报出被零除异常。下溢异常的检测与上溢异常的检测方法基本一致，需要检测是否产生下溢时，在使浮点数减小的浮点运算指令前后检测FPCR寄存器第55位是否发生变化(由0变为1)。

3.2 检测过程分析

检测的主要流程为在源码编译时动态检测相关指令，检测到相关指令后，对其前后进行插桩，插桩内容为检测指令运算前后FPCR的值，运行时对比FPCR对应异常位是否发生变化。如果发生改变，记录并输出当前对应的异常类型、相应的指令操作及输入参数至文件内。具体检测过程如图1所示。此外，也可以将异常触发的条件当作插桩的内容，放在相应的指令操作之后，判断是否触发异常，如通过对比结果是否大于相应浮点类型能表示的最大值来判断是否产生上溢。除通过检测浮点控制寄存器FPCR值的变化外，还可以通过IEEE-754标准定义的产生异常的条件进行检测。

Figure 1 Detection process analysis图1 检测过程分析

采用插桩方法检测异常的目的是快速检测出使函数触发异常的输入参数范围以及异常的具体信息，减少后期定位异常的工作量。本文使用的插桩方法是在源码的编译过程中，对生成的汇编指令进行插桩，保证任何函数都可以被检测。插桩的位置在函数实现源码中对浮点数的运算或者转换指令中，对指令的所在行前后进行插桩，通过对比运算前后FPCR的值判断函数在此处是否触发异常。在检测到异常发生时，可选择终止检测或继续执行其余代码。选择继续执行其余代码前，需调用detection函数对此时检测到的异常信息进行记录，以便程序员检查程序中出现的所有异常(不仅仅是第一个)，即当发现异常时，输出一份简短的报告，程序继续执行，不会中止。

检测浮点数学函数实现源码的异常时，除了直接对浮点数学函数源码的相应指令进行插桩检测外，有些异常可以通过对具体异常的产生条件分析出来。如，被零除异常和整数溢出异常的可能触发条件可以限定为FDIVS/FDIVD及FCVTDL/FCVTLW这4条指令的执行，由于可能触发这两类异常的情况较少，可以先检测函数中是否有以上4条指令，对检测内容进行进一步细化。具体而言，可以通过对除法指令FDIVS/FDIVD的搜索，实现对被零除异常的检测；通过对转换指令FCVTDL/FCVTLW的搜索，实现对整数溢出异常的检测。

4 代码覆盖率分析

4.1 测试用例生成

测试用例是用于检测函数异常的输入数据集，通过输入该数据集，对浮点数学函数进行大规模的检测。IEEE-754标准规定，对于32位的浮点数，最高的1位是符号位S，接着的8位是指数位E，剩下的23位为有效数字位M；对于64位的浮点数，最高的1位是符号位S，接着的11位是指数位E，剩下的52位为有效数字位M。本文根据IEEE-754浮点数的规定及浮点数的理论分布生成测试用例。测试用例的生成规则：(1) 符号位[13]，根据定义域区间，判断测试用例的正负属性；(2) 指数位，覆盖输入区间内所有浮点数的指数；(3) 尾数位，针对每一个指数值，产生N个均匀分布的随机数(相对于浮点数分布的基本特征均匀)。上述3部分构成完整的测试用例，保证了测试用例的完整性和有效性，为下一步检测做好了充分的数据准备。

4.2 代码覆盖率

代码覆盖率是一种度量，它描述了对程序源代码的测试程度[14]。这是白盒测试的一种手段，它可以发现测试用例无法覆盖到的程序。测试人员可以创建代码覆盖缺失的测试用例，以提高覆盖率并确定代码覆盖率的定量度量。在大多数情况下，代码覆盖系统会收集有关正在运行程序的信息。它还将其与源代码信息相结合，以生成有关测试套件的代码覆盖率报告。代码覆盖率可以帮助评估测试的效率，提供定量测量手段，可以了解对代码的测试程度。

统计代码覆盖率可以明确测试过程中软件的运行情况，从而对测试结果进行评估。在本文中使用代码覆盖率的目的是为了在检测过程中，通过查看代码覆盖率来检验对各个函数检测的全面性，避免漏报。可以根据代码覆盖率相应调整测试用例，以达到对浮点数学函数全面检测的目的。

本文在AFL(American Fuzzy Lop)的基础上对代码覆盖率部分进行移植修改，使其能够在申威平台上正常使用。统计代码覆盖率的主要流程如图2所示。左上图表示插桩前的一个函数，b0 (block 0)表示一个基本块,即程序顺序执行的语句序列。在每个基本块的开始插入代码覆盖率计算指令。计算指令的内容为表示一个块的随机数和命中处理函数。当运行测试程序时，把随机数运算的结果作为地址，该地址指向的内容加一完成记录。用随机数R0表示基本块b0的标识，用*((R0≫1)^R1)++表示从基本块b0跳转到基本块b1执行了一次。详细解释如图2所示。

Figure 2 Code coverage process图2 代码覆盖率流程

5 实验及结果分析

本文将实现的浮点异常检测方法应用于申威高性能数学函数库中的浮点数学函数。函数库由基础函数库及SIMD扩展数学库组成，本文主要研究基础数学库，基础数学库的函数分类主要包括三角函数、反三角函数、指数对数函数、贝塞尔函数及其他函数等初等函数。在下面的检测中，对部分函数的检测结果进行了分析，包括sin、cos、logf等函数。

5.1 实验流程

根据申威1621处理器对浮点运算的定义及对浮点控制寄存器FPCR的设置，当输入操作数没有产生异常时，对正常浮点运算的中间结果，先进行舍入，后根据不同的舍入方式来判断异常。结果产生异常时，会在FPCR中记录相应异常标志位。以此对该基础数学函数库进行检测。在用于检测的测试用例生成后，开始对程序进行大规模检测。

首先，在相应的浮点域内，生成均匀分布的浮点数数据。该均匀分布的数据集基于浮点数分布的基本特征[15]，符合IEEE-754浮点数的理论分布：数字越接近零，数据分布越密集；数字离零越远，数据分布越稀疏。其次，在完成对上一步生成的数据测试后，在测试结果文件内，查看函数在哪些数据或哪些位置产生异常的频率较高，分析出异常热点数据。以此热点数据为数据中心，在该数据周围生成大量数据集用于进一步测试。最后，在某一数据周围生成了测试集后，对函数进行有针对性的大规模测试，得出最终结果。测试用例的完整性和有效性对测试的代码覆盖率有一定影响。检测具体流程如图3所示。

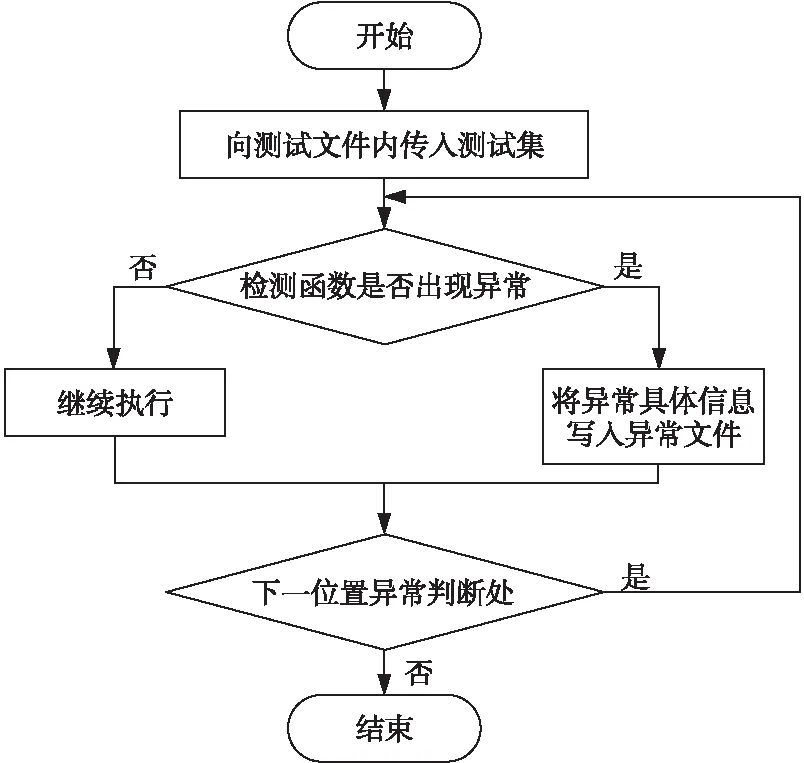
Figure 3 Test flow chart图3 检测流程图

5.2 实验结果分析

(1) 按照上述检测流程，如表1所示为部分函数检测过程中产生异常的参数及其异常类型。代码覆盖率的结果为数据集在测试过程中记录函数中的代码被测试到的比例。代码覆盖率越高，测试结果的可信度越高。对代码覆盖率的统计结果显示,本文生成的测试集可以检测到函数的所有代码分支。开发人员可以根据该结果对函数进行进一步处理。

Table 1 Test results

(2) 152个函数中各异常(上溢、下溢、被零除和无效操作)出现的函数个数，统计结果如表2所示。在检测时，发现输入特殊数NaN并没有触发无效操作异常，即函数未对特殊数NaN进行处理。在此检测结果基础上，对NaN进行了特殊数的处理，处理主要依据NaN是唯一一个与自身不相等的存在。检测到异常进行报告是必须的，收到报告进行处理可以最大程度降低发生意外的可能。

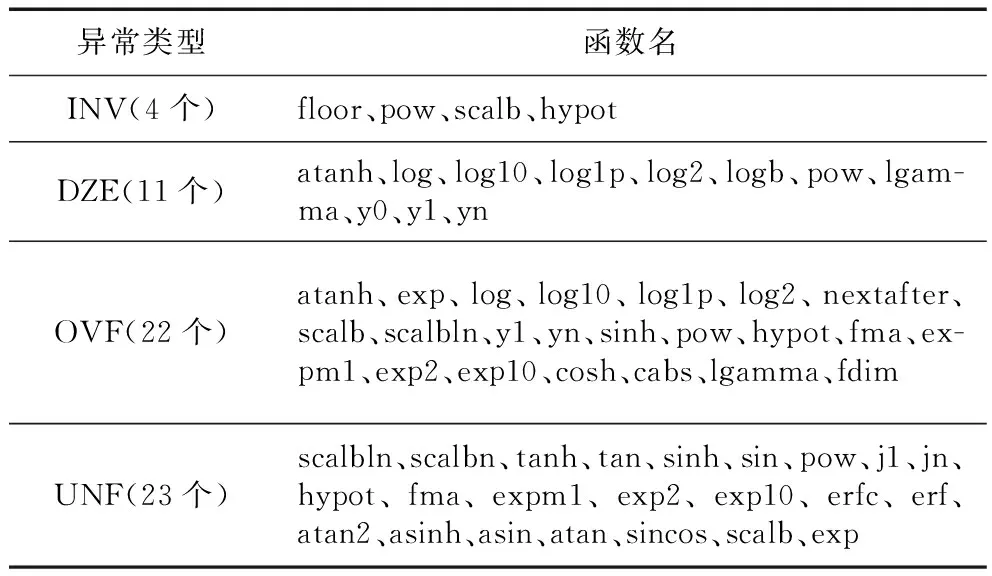
Table 2 Exception functions

(3) 加入插桩检测后的性能变化。

图4对部分有上溢异常的函数插桩检测前后的性能进行了对比，节拍数的变化如图4所示。性能测试结果显示：经过插桩检测后，函数的平均性能降低了38.43%((插桩后节拍数-插桩前节拍数)/插桩前节拍数)；插桩后的运行速度虽然有下降，但对于大多数函数而言，进行插桩异常检测带来了几拍到几十拍的性能消耗，在可接受的范围内。

Figure 4 Performance comparison before and after pile insertion testing图4 插桩检测前后的性能对比

需要特别说明的是，检测出的异常是否会对系统造成重大不良影响，需要开发人员对检测出的异常进行进一步的分析。浮点数的表示精度有限，不能精确表示出实数，部分异常是由可表示精度有限导致的。因此，开发人员可以通过分析检测出异常信息，对异常进行进一步的判断。

上述测试结果表明，该浮点异常检测方法科学有效，插桩后的函数具有检测浮点异常的功能。既满足了对浮点数学函数异常的检测，也满足了对函数性能干扰尽量小的要求。实验数据表明，上溢出和下溢出异常在所有发生的异常中占有较大的比例，对特殊数的检测中无效操作异常发生较多，被零除异常发生较少。当面临大量复杂程序时，检测的计算量变大，将会导致性能下降较多，这点后续需继续优化。本文提出了浮点异常分类检测方法，以尽可能全面地在测试阶段发现异常。