MEMS陀螺仪随机误差分析与建模
2022-06-23张萌,王虹,吕东
张 萌, 王 虹, 吕 东
(南京理工大学,南京 210000)
0 引言
MEMS(Micro-Electro-Mechanical System)陀螺仪具有尺寸较小、成本低廉、集成度高、可靠性好等一系列优点,在惯性导航、工业控制、航空航天及电子产品等领域得到广泛的应用。在军事方面,常规武器的制导化与战术制导武器的小型化已成为各国武器装备的发展趋势[1]。而制导武器所需的陀螺仪精度较高,受微机械工作原理、构造及加工制作水平的影响,MEMS陀螺仪的测量精度往往无法满足武器装备信息化、数字化的使用需求,极大地制约了MEMS陀螺仪的发展和应用。特别是MEMS陀螺仪随机漂移误差,没有明确的出现规律且较易受到外界环境的影响,是限制陀螺仪精度提高的主要因素。陀螺仪的随机漂移误差是由外干扰力矩引起的,随时间做无规律变化,并且较易受到周围环境的影响,严重限制陀螺仪精度提高。由此,本文针对MEMS陀螺仪采集的原始静态数据,运用改进的Allan方差分析法辨识其随机误差成分,得出各项误差的特征参数,建立随机误差的自回归滑动平均(Auto-Regressive and Moving Average,ARMA)模型。
1 MEMS随机误差分析
MEMS陀螺仪随机误差辨识方法主要有自相关分析法、功率谱密度法和Allan方差分析法等[2]。其中:自相关分析法需要长时间的数据采集才能取得较好的效果,分析效率低;功率谱密度法从频域角度分析误差,但难以通过功率谱密度分离误差;Allan方差能细致地辨识各项误差源,计算简便。
1.1 Allan方差与随机误差关系
假设MEMS陀螺仪输出的各误差相互独立,则Allan方差和MEMS陀螺仪的双边功率谱间有唯一确定的关系,即
(1)
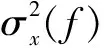
研究表明,MEMS陀螺仪的随机误差主要包括量化噪声、角度随机游走、零偏不稳定性、角速率随机游走和速率斜坡,可用Allan方差分别表示[3]。
1)量化噪声(Quantization Noise)。
量化噪声由A/D转换过程产生,在采样瞬间的误差是随机且不相关的,其Allan方差为
(2)
式中,Q为量化噪声的方差。
2)角度随机游走(Angle Random Walk)。
角度随机游走是MEMS陀螺仪输出的角速度白噪声的时间积分,其Allan方差为
(3)
式中,N2为白噪声功率谱密度。
3)零偏不稳定性(Bias Instability)。
零偏不稳定性误差源自电子线路和其他元件的闪烁噪声,主要指低频的零偏抖动,其可描述为
(4)
式中,B为零偏不稳定系数。
4)角速率随机游走(Angle Rate Random Walk)。
角速率随机误差来源不确定,可能是由MEMS陀螺仪内部晶振老化引起的,其Allan方差为
(5)
式中,K为角速率随机游走系数。
5)速率斜坡(Rate Ramp)。
漂移速率斜坡可以认为是确定性误差,可表示为
(6)
式中,R为速率斜坡系数。
1.2 改进Allan方差原理
经典Allan方差对MEMS陀螺仪的随机误差分辨率较低,随机误差项出现时间模糊[4]。本文采用改进Allan方差法分析MEMS陀螺仪数据,其原理描述如下。
设置MEMS陀螺仪的采样时间间隔为τ0,得到总数为L的数据样本ω1(τ0),ω2(τ0),…,ωL(τ0),将数据划分为不同长度的子集,每个子集的采样间隔为τ=nτ0,n=1,2,3,…,N1(N1≤(L-1)/2)[5]。当n≥2时,对数据样本进行两次分组,分别计算其Allan方差,取二者均值作为该组Allan方差值。
当n=1时,角速率序列分组为:ω1(τ0),ω2(τ0),…,ωk(τ0)。当n=2时,两次分组的数据序列如图1所示。

图1 n=2时数据的分组情况
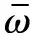
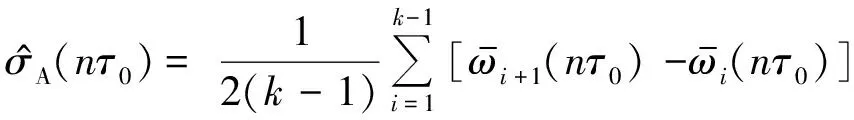
(7)


(8)
1.3 数据采集与误差辨识
以STM32F103T8U6为核心芯片搭建MEMS陀螺仪数据采集系统,利用USB接口将采集到的陀螺仪静态数据实时传输至PC机。本文所用的实验对象是1933GST2202003,设置温箱为30 ℃,陀螺仪保温1 h,采集数据如图2(a)所示,陀螺仪输出数据均值为3.047 8(°)/s。计算改进Allan方差并绘制双对数曲线如图2(b)所示。
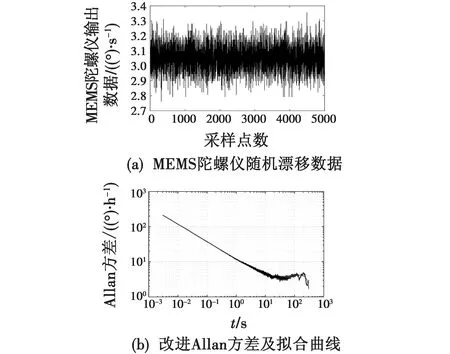
图2 MEMS陀螺仪随机漂移数据和改进Allan方差及拟合曲线
利用最小二乘法拟合陀螺仪误差参数,与经典Allan方差对比,结果如表1所示[6]。主要误差表现为零偏不稳定性、角速率随机游走以及速率斜坡。
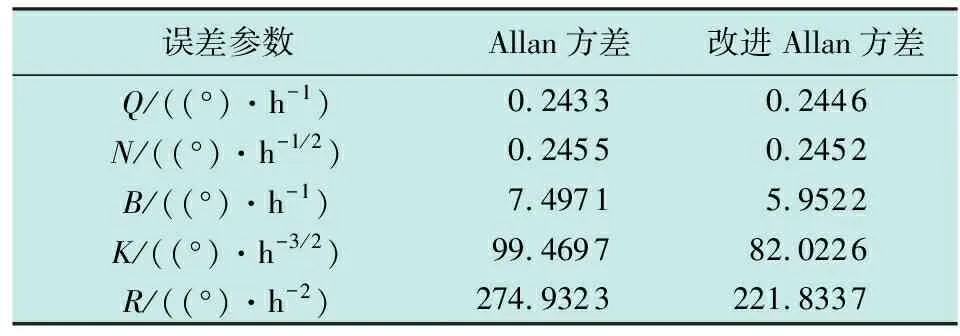
表1 改进前、后Allan方差对比
改进前、后Allan方差的分析结果与产品提供的特征参数进行对比,零偏不稳定性、角速率随机游走和速率斜坡分别减少20.61%,17.54%,19.31%。本文改进Allan方差的分析结果更加接近产品提供的特征参数,结果表明,改进后的Allan方差分析效果更优。
2 MEMS陀螺仪随机误差建模
时间序列方法是一种经典的信号处理方法,广泛应用于陀螺仪随机误差建模领域[7]。
2.1 MEMS陀螺仪数据预处理
时间序列建模所用数据为满足零均值、平稳、正态等条件的随机序列,因采集环境及MEMS陀螺仪工艺等问题,其输出一般不满足建模条件。因此,在建模前需要对数据进行预处理和数据检验[8]。
建模数据的预处理过程可分为野值剔除、零均值处理和趋势项剔除3步。
1)野值剔除:MEMS陀螺仪野值是指采集过程中受到周围环境影响产生的粗大误差,根据莱依达准则剔除野值的依据是以3倍标准差为阈值,将超过此值的数据剔除。
2)零均值处理:受采集系统的硬件及温度等影响,原始数据一般为非零均值序列,将1)中数据均减去序列均值,即可得到零均值序列。
3)趋势项剔除:选用最小二乘法拟合MEMS陀螺仪静态数据中的趋势项参数,零均值序列减去趋势项即可。
MEMS陀螺仪原始数据与预处理后的数据见图3。

图3 MEME陀螺仪原始数据及预处理后数据
2.2 MEMS陀螺仪数据检验
MEMS陀螺仪数据检验包括平稳性检验与正态性检验,一般认为陀螺仪的输出数据服从正态分布,主要对平稳性进行检验。
采用逆序检验法对预处理数据进行平稳性检验,设预处理后的时间序列为x1,x2,x3,…,xn,n≤L,将其分成I个子序列,求出每个子序列的均值{u1,u2,u3,…,ui},对于其中任一均值up(p≤i),若有up>uq(p (9) (10) Rvar=I(2I2+3I-5)/72 (11) (12) 当取显著水平a=0.05时,若|Z|≤1.96,则该序列为平稳序列[9]。 将预处理后的数据分成10组,按上述方法计算Z的值为0.214 1,满足平稳性要求,认为处理后的数据适用于时间序列建模。 经过数据预处理及检验,可通过建立时间序列模型来拟合陀螺仪随机误差,最常用的模型为自回归模型(AR)、滑动平均模型(MA)以及结合两者的自回归滑动平均模型[10]。MEMS陀螺仪输出数据的时域递推形式,即ARMA(p,q)模型,为 (13) 式中:ε(n)为高斯白噪声;φk为自回归系数;φk为滑动平均系数。p=0时,式(13)为MA(q)模型;q=0时,式(13)为AR(p)模型。具体模型可由数据的自相关函数(ACF)与偏自相关函数(PACF)确定[11],如表2所示。MEMS陀螺仪的自相关函数与偏自相关函数见图4。 表2 平稳时间序列自相关和偏自相关函数特征 图4 MEMS陀螺仪的自相关函数与偏自相关函数 如图4所示,自相关函数与偏自相关函数均表现出明显的拖尾性,适用ARMA(p,q)模型。 模型阶次可由最小信息准则(AIC)和贝叶斯信息准则(BIC)确定[12]。AIC是一种广泛应用的ARMA模型的定阶准则,定义为 (14) AIC应用于简单的时间序列模型,在分析大样本时,确定的模型阶次比真实的阶数高。BIC弥补了AIC的缺陷,其定义为 (15) 计算MEMS陀螺仪的AIC与BIC值,ARMA(1,1)模型的值使二者最小,故选择ARMA(1,1)建立MEMS陀螺仪随机误差模型,即 x(t)=0.476 425x(t-1)+ε(t)-0.455 909ε(t-1) (16) 式中,ε(t)~N(0,0.006 3)。 经上述过程得到所选MEMS陀螺仪的漂移误差模型(即式(16)),绘制预处理后实验数据与建模结果前100 点,对比结果如图5所示。 图5 随机误差与建模结果对比 陀螺仪的随机漂移误差可认为是白噪声过程,当陀螺仪上电后,输出逐渐平稳,可假定此时的输出数据为该陀螺仪的随机漂移误差,因此适用于式(16)模型。陀螺仪处于振动环境时的误差为静态时的误差叠加振动输入相关的误差,也可用式(16)模型代替该陀螺仪静态时的误差。 陀螺仪的刻度因素误差、安装误差和确定性漂移能够通过标定实验进行补偿,但剩余的随机漂移误差却无法通过标定来确定,本文采用的实验数据为标定后的陀螺仪输出数据,所建立的模型为陀螺仪随机漂移误差模型。 本文采用改进Allan方差法对实测陀螺仪数据进行分析,确定各项误差的特征参数,与产品提供数据手册对比可知,用改进Allan方差分析MEMS 陀螺仪随机误差是有效的。对预处理后的陀螺仪X轴数据建立时间序列模型,在误差允许范围内,陀螺仪随机误差与建模数据基本一致,实现了MEMS陀螺仪随机误差的时间序列建模。2.3 检验模型识别与定阶


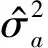

3 结束语
