基于MOA-VMD的轴承多维健康指标构建方法

王道嵘，梁涛，王建辉，姜文

(1.河北工业大学 人工智能与数据科学学院，天津 300130；2.河北建投能源投资股份有限公司，石家庄 050011)

轴承作为一种机械标准件，广泛应用于各种旋转机械设备，轴承健康度的预测对于各种旋转机械的运维具有重要的意义[1]。轴承健康度预测技术可以分为基于物理模型的方法与数据驱动的方法两类[2]：由于设备的结构、机理、运行环境等错综复杂，基于物理模型的方法难以建立起适用性强的模型；数据驱动的方法通过分析、处理轴承振动信号数据建立振动信号与轴承健康度的映射关系模型，从而预测轴承的健康度，是目前的主流方法。随着机器学习的发展，更使得基于数据驱动的健康度预测成为国内外研究的重点方向[3]。

从轴承振动信号中提取出退化特征信息并将其构建为用于描述轴承健康度的指标，称为健康指标(Health Indicator，HI)，其构建的优劣将直接影响模型预测的准确性[4]。很多学者对健康指标的构建进行了大量的研究。文献[5]使用dispersion-entropy描述设备的退化过程；文献[6]用变分自编码器对轴承原始信号进行处理，提取并学习轴承的故障特征，用于轴承的故障诊断；文献[7]利用WP-EMD 提取轴承振动信号特征，利用自组织竞争网络进行融合并生成健康指标；文献[8]计算了多个时、频域的特征指标，选择与剩余使用寿命相关性强的几个特征输入循环神经网络构建健康指标；文献[9]用t-SNE方法处理轴承振动信号来提取相关特征，得到了性能更好的健康指标：上述研究采用的特征信息类型大都比较单一，没有综合考虑各种类型的特征；而且大多数学者都选择构建一个一维的单调健康指标描述当前的健康度，导致所构建健康指标中包含的健康度信息不够充分，也导致其提取的特征只能识别出健康度，并不能同时提取工况等信息。

针对以上问题，本文提出了一种多维健康指标的构建方法，通过蜉蝣优化算法(Mayfly Optimization Algorithm，MOA)优化参数后的变分模态分解(Variational Mode Decomposition，VMD)对轴承振动信号进行去噪，针对去噪信号选取合适的特征组成特征向量并降维后得到三维健康指标，验证健康指标的可靠性后将其送入支持向量机(Support Vector Machine，SVM)分类器与长短期记忆(Long Short-Term Memory，LSTM)神经网络进行工况识别与健康度预测。

1 振动信号去噪

1.1 变分模态分解

变分模态分解能够自适应地实现信号的频域剖分及各分量的有效分离，且可以自由确定模态分解的个数[10]， 将变分模态分解后的模态分量定义为一个幅频调制信号，分解个数为K，则第k个分量的表达式为

uk(t)=Ak(t)cos[φk(t)]；k∈{1,…,K} ，

(1)

式中：uk(t)为谐波信号；Ak(t)为uk(t)的瞬时幅值；φk(t)为相位，其一阶导数表示瞬时频率。

变分模态分解的约束模型公式为

式中：x为原始信号，是各分量uk的累加；ωk为各分量的中心频率；δ(t)为脉冲函数。

为得到变分问题的最优解，引入增广的拉格朗日函数，即

L({uk},{ωk},λ)=

(3)

式中：λ(t)为拉格朗日乘子；α为二次惩罚因子。用交替方向乘子算法迭代更新un+1，wn+1，λn+1，可求得(3)式中的“鞍点”，即(2)式的最优解。

1.2 蜉蝣算法优化变分模态分解参数

在变分模态分解处理过程中，分解个数K和惩罚参数α均会极大地影响其分解效果，而其他参数对分解效果的影响则较小[11]，因此，设置tau=0,init=1,DC=0,ε=1.0×10-7，分析变分模态分解前如何选取适当的K和α。

蜉蝣优化算法是一种新的仿真优化算法，用于解决复杂的函数优化问题。蜉蝣优化算法由雌性蜉蝣群体和雄性蜉蝣群体组成，受蜉蝣动物的交配行为启发，将雄性蜉蝣的最优个体和雌性蜉蝣的最优个体进行交配，得到一个最优子代。同理，雄性次优个体与雌性次优个体进行交配得到次优的个体。这一过程与适者生存的规律一样，逐步淘汰适应度较差的个体[12]。

最初，随机产生2组蜉蝣，分别代表雄性和雌性种群。也就是说，每个蜉蝣被随机放置在问题空间中，作为由d维向量表示的候选解x= (x1,…,xd),并根据预先确定的目标函数f(x)对其性能进行评价。蜉蝣的速度v=(v1,…,vd)定义为其位置的变化，每个蜉蝣的飞行方向是个体和社会飞行经验的动态交互作用。每个蜉蝣都会调整自己的轨迹，使其朝向目前为止的个人最佳位置(pbest)以及迄今为止群中任何蜉蝣所获得的最佳位置(gbest)。雌、雄性蜉蝣具有不同的运动特点：雄性蜉蝣成群的聚集，意味着每只雄性蜉蝣的位置都是根据自己和周围蜉蝣的经验来调整，而雌性蜉蝣则不会成群聚集，它们会飞到雄性群体中来繁殖。蜉蝣交配行为则用交叉算子来表示，基于个体的适应度函数来选择亲本，最好的雌性与最好的雄性繁殖，次好的雌性与次好的雄性繁殖。交叉的结果是产生2个后代。其寻优步骤见表1。

表1 蜉蝣优化算法的寻优步骤

为了验证蜉蝣优化算法的收敛性和优化性能，将(4)式作为适应度函数，选择遗传算法(Genetic Algorithm，GA)、粒子群优化(Particle Swarm Optimization，PSO)算法进行性能对比。

(4)

设置遗传算法的迭代次数为100，种群规模为100，交叉概率为1，变异概率为0.01；粒子群优化算法迭代次数为100，种群规模为100；设置蜉蝣优化算法迭代次数为100，种群数量为100。3种算法的优化迭代曲线如图1所示：粒子群优化算法和遗传算法都陷入了局部最优解，蜉蝣优化算法的迭代速度优于其他2种算法且其得到的最优值更加接近理论最优值。说明相对于遗传算法与粒子群优化算法，蜉蝣优化算法具有更快的收敛速度和更强的全局搜索能力。

图1 不同算法的优化迭代曲线

用蜉蝣优化算法对变分模态分解的参数进行优化时需要选定合适的适应度函数。轴承振动信号经过变分模态分解后各分量的包络熵值Ep可反应出该分量的稀疏特性[13]。如果分量中包含的噪声较多，会掩盖信号的冲击特征，则该分量的稀疏性较弱，包络熵较大；反之，则包络熵较小。选择每次分解后所有分量中包络熵值中最小的一个作为局部最小包络熵minEp，该最小熵值对应的分量有着丰富的特征信息。包络熵Ep的计算公式为

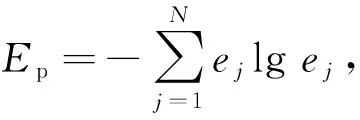
(5)

式中：ej为a(j)量纲一化的结果；a(j)为x(j)经希尔伯特解调得到的包络信号。

将局部最小包络熵作为参数优化的适应度函数，整个搜索过程就是要找到全局最小包络熵以及对应的最佳分量所在的最优参数组合[K,α]。

1.3 相关性

相关系数是反映变量之间相关关系密切程度的指标。这里采用皮尔逊相关系数来分析K个分量与原始信号的相关性。设样本X和样本Y，则两者的相关系数为

(6)

式中：r为相关系数；Cov(X,Y)为样本X与样本Y的协方差；D(X)，D(Y)分别为样本X，Y的方差。r越大，代表样本间的相关性越高。计算各个分量与原始振动信号的相关系数，挑选最能代表原始信号的部分分量重构信号以达到降噪目的[14]。

2 特征选取

随着轴承的退化，普通时域下的简单特征会呈现出明显变化，但这些简单特征的变化往往呈现为“阶段性”，单独采用这类特征会使得退化特征信息的提取效果较差；奇异值分解可以将包含信号特征信息的矩阵分解到不同的子空间中，是一种能够在扰动和噪声下保持信号特征相对稳定的特征提取方法[14]；熵类特征一般用来表征信号中所蕴含的各种能量的大小，样本熵可以反映出时间序列的复杂性，序列的复杂性越高，样本熵的值就越大[15]，能量熵则会随着振动信号的能量分布而发生变化[16]：综上，选择重构信号的最大值、标准值、峭度以及主要分量的奇异值、样本熵、能量熵作为提取的多维特征。

t分布随机邻近嵌入(t-SNE)算法是一种深度学习的非线性流行学习算法，对高维非线性数据集有优异的降维效果[15]，其核心是引入自由度为1的分布函数代替高斯分布，构建高维空间数据样本的概率分布，并在低维子空间构建对应样本的概率分布，采用KL散度(相对熵)衡量高低维空间概率分布的相似程度，从而实现降维。

3 轴承多维健康指标构建方法

基于上述理论，轴承多维健康指标构建方法的流程如图2所示，具体步骤如下：

1)获取轴承的振动信号。

2)利用蜉蝣优化算法优化变分模态分解参数[K0,α0]，用寻优得到的最优参数分解振动信号，得到K0个分量。

3)计算各分量与原始信号的相关性，得到相关性最高的3个分量进行信号重构。

4)计算重构信号的最大值、平均值、峭度以及3个分量的奇异值、样本熵、能量熵，得到12维特征向量。

5)用t-SNE降维方法将12维特征向量降至3维。

6)将训练集的特征向量输入用蜉蝣优化算法优化参数的SVM分类器和LSTM神经网络进行训练，分别得到工况分类模型与健康度预测模型。

7)将测试集的特征向量输入2个模型，验证模型的可靠性。

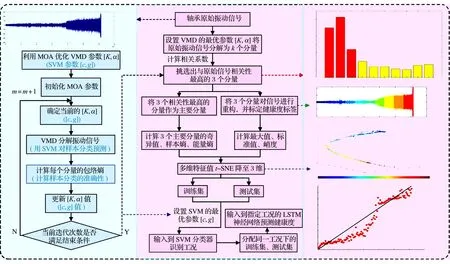
图2 轴承多维健康指标构建方法的流程图

4 试验验证

4.1 数据描述

选用XJTU-SY数据集验证方法的有效性，该数据集通过维持固定的径向力和转速保持高负载来加速轴承的退化，从而获取测试轴承全寿命周期的振动数据，试验轴承型号为LDK UER204，相关参数见表2[17]。

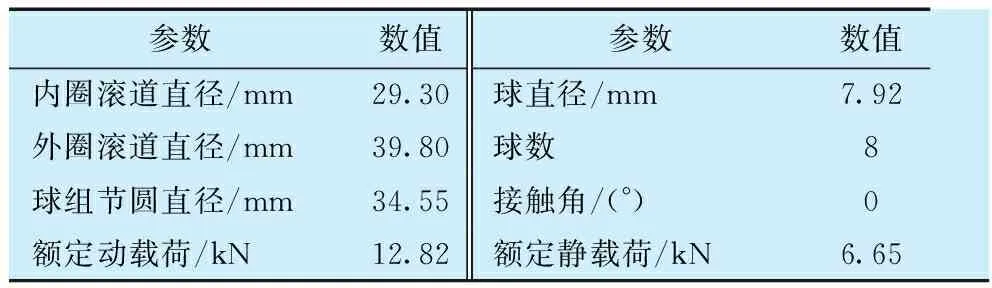
表 2 LDK UER204轴承的参数

设置采样频率为 25.6 kHz，采样间隔为 1 min。2个加速度传感器分别用于测量轴承水平与垂直方向上的信号。忽略出现的混合故障，以及与其他数据有明显差异的数据。数据共有3类工况，每类工况下有4套轴承。工况数据和轴承寿命数据见表3。

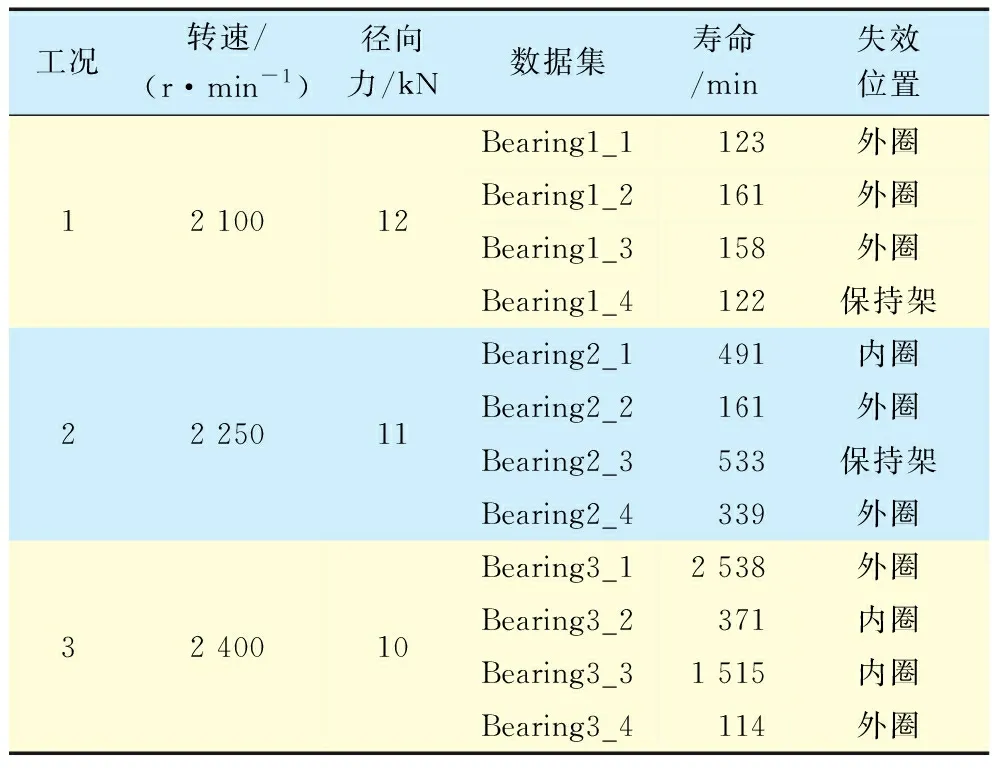
表3 试验轴承工况及其寿命数据

Bearing1_1水平、垂直方向的全寿命周期振动信号如图3所示，对比表明水平方向振动信号的振幅明显大于垂直方向，更有利于对信号进行试验研究，故只选取了水平方向信号进行后续分析。

图3 水平与垂直方向的信号对比

4.2 数据处理

轴承原始振动信号往往包含着大量噪声，严重影响特征信息的提取，因此在特征提取之前对信号进行一次“去噪”很有必要。每进行一次采样得到32 768个点，截取前10 000个样本点作为试验数据，数据采样示意图如图4所示。

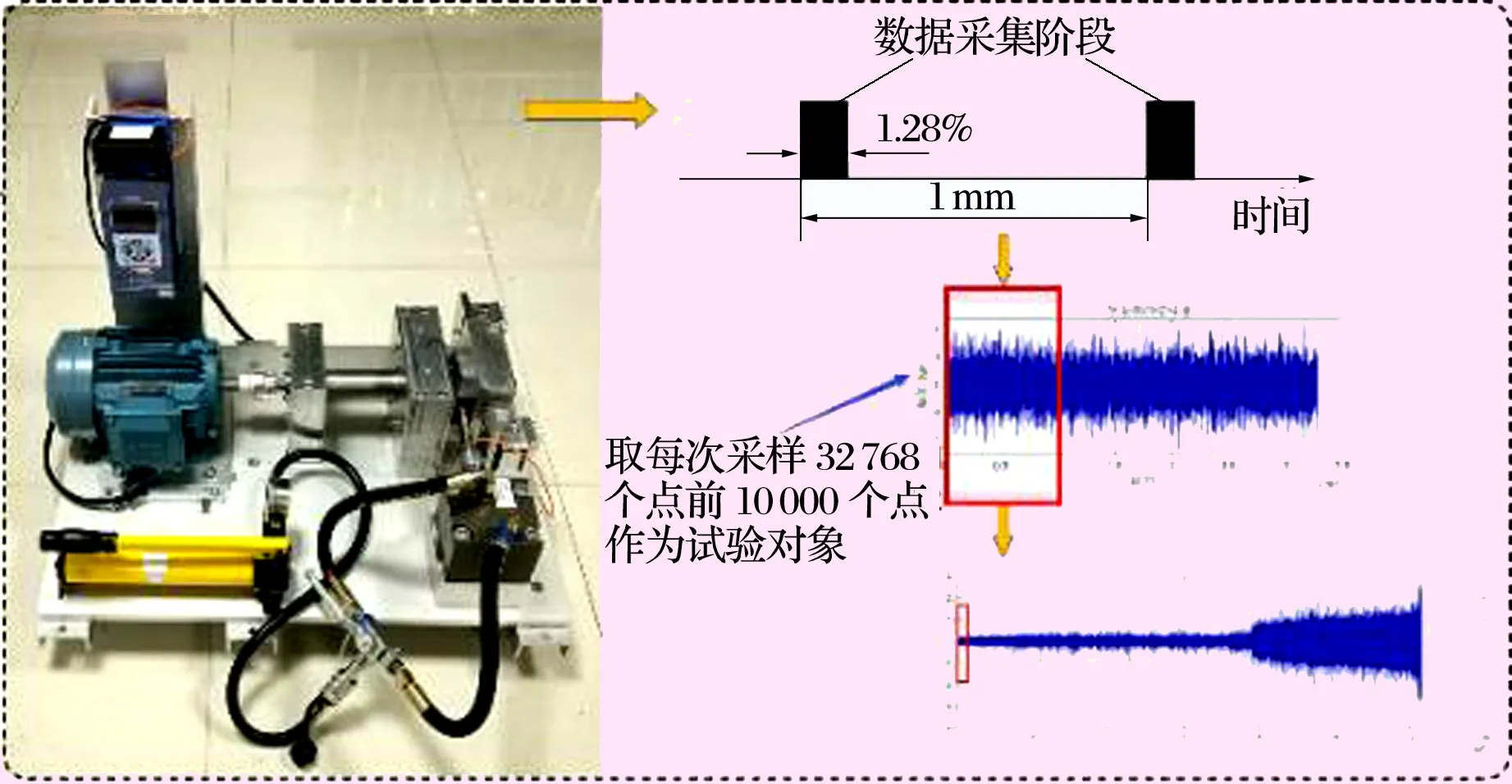
图4 数据采样示意图

利用蜉蝣优化算法对变分模态分解的参数组合[K0,α0]进行寻优，寻优目标是使得分解后各分量的最小包络熵Ep值最小。这里以一个采样点的数据为例(一个采样点指的是进行一次数据采样得到的10 000个数据点)，得到的最优参数组合为α=4 000,K=10，对每个采样点的10 000个数据进行变分模态分解，得到10个分量。

每个分量与原始信号的相关系数如图5所示，选择与原始信号相关性最高的3个分量重构信号。Bearing1_1的振动信号及其重构信号如图6所示，可以看出重构信号边缘的高频噪声明显减少，从去噪信号中更容易提取轴承的相关特征信息。

图5 各分量与原始信号的相关程度

图6 Bearing1_1数据去噪前、后的时域图

4.3 特征提取

计算重构信号每个采样点的最大值、平均值、峭度以及相关性最高3个分量的奇异值、样本熵、能量熵，组成12维特征量，再利用t-SNE降维降至3维，进行特征量可视化。

4.3.1 工况特征

取12套轴承的全寿命周期数据(Bearing3_1与Bearing3_3数据量过大，分别为2 538与1 515个数据点，故每隔10个点取样一次，最后取得253与151个数据点)，求得3维特征进行可视化(图7)，红色、绿色、蓝色的点分别用来代表工况1，2，3下的数据。从图7可以看出，3种工况的数据呈不同的曲线分布，不同工况部分有较好的分离效果，重叠部分较少。

图7 不同工况下轴承数据特征提取的可视化

4.3.2 健康度特征

将工况1下4套轴承所提取的3维特征进行可视化，结果如图8所示，图下方的色谱条从蓝色到红色代表轴承数据从正常逐渐到故障，不同形状代表工况1下4种不同的轴承数据。

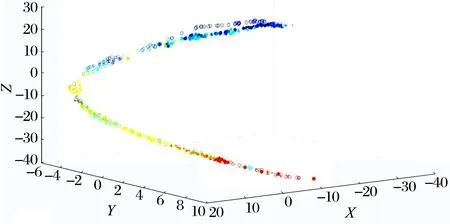
(a)本文所提方法

图8a是通过本文所提方法得到的可视化视图，可以看出振动信号从正常状态至损坏状态在三维空间中几乎呈一条曲线分布， 具有很好的聚集性与连续性，特征点所处空间的位置能很大程度地反映轴承健康状况。 图8b由相关性最强的3个分量的最大值、标准值和峭度所组成的9维特征量降维所得，图8c则由这3个分量的奇异值、能量熵和样本熵所组成的9维特征量降维得到，可以看出这2种情况均不能很好表征轴承的退化情况。

4.4 故障分类与剩余寿命预测

4.4.1 故障分类

取4.3.1节得到的3维特征数据进行故障分类试验，12套轴承共计2 977个数据点，将数据顺序打乱，划分前2 477个数据点为训练集，剩余500个数据点作为测试集，利用支持向量机对故障进行分类处理，每个数据点的3维特征作为输入，工况标签作为输出。

支持向量机进行分类预测时需要调节惩罚参数c与核函数参数g以得到最佳参数组合[c0,g0]，从而使分类预测效果最佳。同样，利用蜉蝣优化算法对支持向量机的这2个参数进行优化，适应度函数为分类准确率的相反数，当其最小时，即分类准确率最高。通过寻优得到最佳参数组合c=100，g=0.1，分类结果如图9所示，测试集中，499个数据点实现了正确分类，准确率为99.8%，效果理想。

图9 轴承故障的支持向量机分类结果

4.4.2 健康度预测

将轴承的健康度标签Y定义为

(7)

式中：Xnow为轴承当前剩余寿命；Xall为轴承总寿命。初始健康标签Y为0，随着轴承运行状态逐渐恶化，Y最后变为1，这样就把轴承的健康度标签归至0与1之间。

长短期记忆神经网络作为循环神经网络的变体，能够解决循环神经网络长序列训练过程中的梯度消失和梯度爆炸问题，可以很好地捕捉时间序列上的特征，是用于剩余寿命预测的一种经典神经网络模型。本文选择长短期记忆神经网络预测轴承健康度，用提取的3维特征作为输入，对应的健康度标签作为输出。

取第1个工况下4套轴承的的数据，共计564个采样点，所提取的特征数据为R564*3，划分Bearing1_1的123个数据为测试集，其他轴承的441个数据为训练集，训练长短期记忆神经网络并进行测试。试验结果如图10所示，仅通过当前一个时间点振动信号提取的特征，即可得到相对不错的健康度预测效果，验证了所构建健康指标的合理性。

图10 工况1下试验轴承长短期记忆神经网络的 健康度预测结果

5 结束语

利用蜉蝣优化算法优化变分模态分解的参数，以各分量的最小包络熵作为适应度函数，可以获得比遗传算法和粒子群优化算法更好的准确性与收敛性；以最大值、平均值、峭度以及主要分量的奇异值、样本熵、能量熵作为特征量组合，将其降维后含有轴承的工况与健康度信息在三维空间中直观展现出来，通过三维健康指标在空间中呈现一条代表轴承健康度逐渐变化的过程曲线，作为神经网络的输入时能提供更多的特征量信息。