精密轴系最优径、轴向载荷比分析
2022-06-22赵雁夏玉磊廖辉谢鹏飞张致远
赵雁,夏玉磊,廖辉,3,谢鹏飞,张致远
(1.洛阳轴承研究所有限公司,河南 洛阳 471039;2.河南省机床主轴工程技术研究中心,河南 洛阳 471039;3.西北工业大学 机电工程学院,西安 710071)
随着金属材料冶炼技术的进步,延寿技术的发展[1-2]以及润滑可靠性的提高[3-4],精密轴系轴承的承载能力和疲劳寿命已不再是主要研究对象,其运转精度和稳定性的提升已成为其发展的关键[5]。
径、轴向载荷比是影响精密轴系轴承运转稳定性的重要参数之一。目前,该方面的研究主要集中在轴向载荷对轴承或主轴相关性能的影响,而忽略了径、轴向载荷比的关联关系:文献[6]分析了高速角接触球轴承的运动学特征,研究表明施加合适的轴向预载荷可以避免钢球陀螺滑动以及减小自旋滑动; 文献[7]分析了径、 轴向载荷比对圆锥滚子轴承接触应力和额定寿命的影响,结果表明存在合适的载荷比使轴承额定寿命最大;文献[8]分析了轴向预载荷对双列角接触球轴承性能的影响,轴向预载荷过大,轴承旋转灵敏度较小,摩擦功耗增加,轴向预载荷过小,轴承刚度难以满足使用要求,轴系抗振能力较弱;文献[9]分析了定位预紧组配轴承的最小工作预载荷,得到了初始预载荷及最小工作预载荷的关系;文献[10]建立了陀螺角接触球轴承动力学分析模型,结果表明随预紧力减小,陀螺角接触球轴承的摩擦力矩幅值会出现较多的突跳点;文献[11]分析了拧紧力矩对航天器驱动机构轴系摩擦力矩的影响,结果表明轴承摩擦力矩随拧紧力矩增大而增大;文献[12]基于流体动压润滑理论建立了考虑载荷效应的流体滚动阻力矩数学模型,分析了轴承预载荷对主轴静、动态特性的影响,并通过试验验证了模型的正确性;文献[13]通过一对背靠背安装角接触球轴承的轴系振动试验,发现轴承预紧程度对其固有频率和谐响应振幅影响显著;文献[14]建立了五自由度磨床主轴模型,分析了主轴预载荷与刚度和振动的关系,结果表明轴向预载荷使系统的轴向固有频率小于径向固有频率。
本文在上述研究的基础上,建立了精密轴系轴承仿真分析模型,以轴承载荷分布、钢球旋滚比以及轴承摩擦力矩等作为评价指标,分析了径、轴向载荷比对精密轴系轴承动态特性的影响,以确定最优载荷比,并通过试验进行验证。
1 精密轴系模型
精密轴系主轴由2套角接触球轴承共同支承,并施加一定的轴向预载荷,如图1所示。左、右端轴承动力学特性相同,以左端轴承为例分析。为了准确描述精密轴系轴承的运动,建立以下坐标系(下标用l表示):1)以精密轴系中心为原点建立惯性坐标系Oxyz,各零件的位移及作用力均在该坐标系下描述;2)以外圈质心Oe为原点建立外圈坐标系Oexeyeze;3)以内圈质心Oi为原点建立内圈坐标系Oixiyizi;4)以保持架质心Oc为原点建立保持架坐标系Ocxcyczc;5)以球质心Ob为原点建立球坐标系Obxbybzb;6)以保持架兜孔中心Op为原点建立兜孔坐标系Opxpypzp。

图1 精密轴系示意图
1.1 精密轴系运动学分析
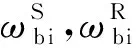
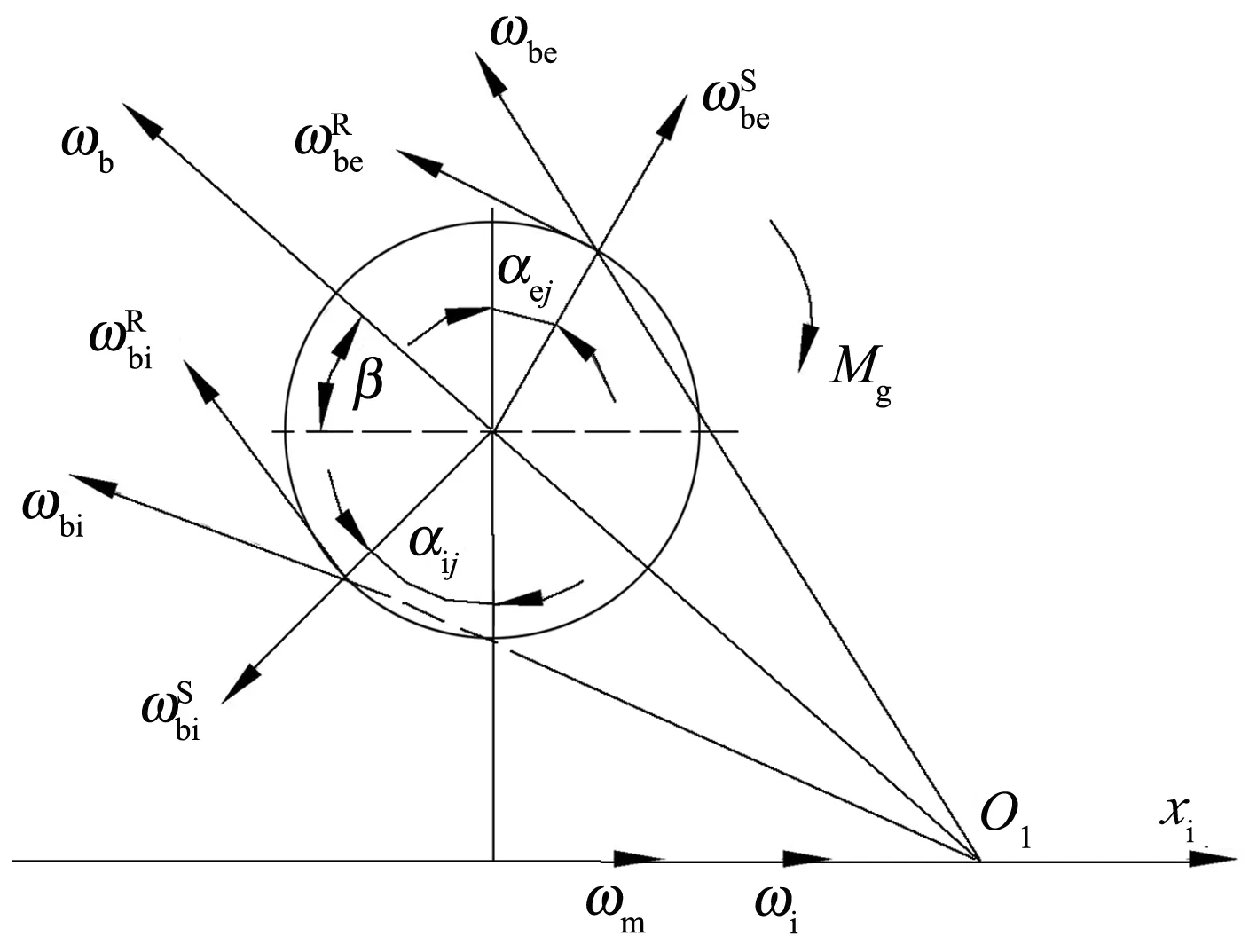
图2 球运动示意图
1.2 球动力学微分方程
在轴、径向载荷联合作用下,球受力如图3所示,图中:Qlij,Qlej为球与内、外圈沟道的法向接触载荷;Tlηej,Tlηij,Tlξej,Tlξij为球与沟道之间的拖动力;Qlczj,Qlcxj为球与保持架在切向和轴向的法向接触载荷;PlRηj,PlRξj为球表面的滚动摩擦阻力;PlSηj,PlSξj为球表面的滑动摩擦阻力;Fhηij,Fhηej,Fhξij,Fhξej为作用在球上的流体动压力的水平分量;Flηij,Flηej,Flξij,Flξej为球与内、外圈沟道接触入口处流体作用产生的滚动摩擦阻力;Jlbx,Jlby,Jlbz为球的转动惯量;Glbyj,Glbzj为球在ylbj,zlbj方向的惯性力矩;下标η,ξ表示球与沟道接触椭圆的长轴和短轴方向;下标i,e表示内、外圈。
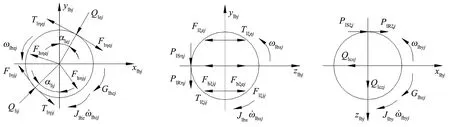
图3 轴、径向载荷联合作用下球受力示意图
球动力学微分方程组为
(1)
式中:mlb为球质量;Dw为球直径;
为球质心加速度;
为球角加速度。
1.3 保持架动力学微分方程
保持架在运动过程中受到引导套圈的作用力、自身重力以及球的作用力,其受力模型如图4所示,图中:Flcy,Flcz,Mlcx分别为引导挡边对保持架的法向力、切向力和力矩;Glc为保持架重力;ψlc为保持架坐标系与外圈坐标系的偏角;φlj为第j个球的方位角(第1个球位置在yle负半轴)。

图4 保持架受力示意图
保持架动力学微分方程组为
(2)
式中:mlc为保持架质量;
为保持架质心加速度;Jlcx,Jlcy,Jlcz为保持架转动惯量;
为保持架角加速度;Z为球数;Dpw为球组节圆直径。
1.4 轴与内圈动力学微分方程
工作过程中内圈与轴配合使用,其整体受力如图5所示,图中:Fr为径向载荷;Fa为轴向预载荷;θ为轴倾角;Ll,Lr为径向载荷作用位置与左、右端轴承的距离。

图5 轴与内圈受力示意图
轴与内圈的动力学微分方程为
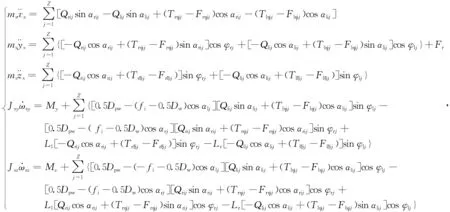
(3)
式中:ms为轴与内圈整体的质量;
为轴与内圈整体的质心加速度;Jsy,Jsz为轴与内圈整体的转动惯量;
为轴与内圈的角加速度;My,Mz为轴与内圈所受的外加力矩;fi为内沟曲率半径系数。
2 仿真分析
以某精密轴系P2级B7005角接触球轴承为研究对象,其主要结构参数见表1,套圈及钢球材料为GCr15,保持架材料为聚酰亚胺,轴系转速为5 000 r/min。基于多体动力学软件建立精密轴系仿真分析模型,采用GSTIFF变步长积分算法[15]求解模型的动力学方程组,分析不同载荷比下轴承的动力学特性。
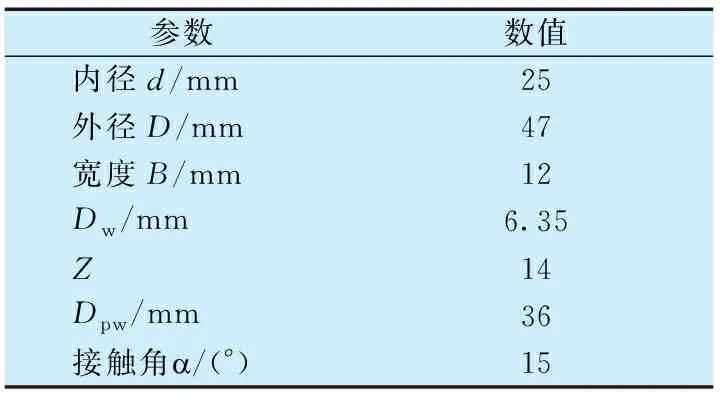
表1 B7005角接触球轴承主要结构参数
2.1 承载特性分析
根据该精密轴系轴承使用经验,取轴向载荷Fa=100 N及一系列径向载荷,分析不同径、轴向载荷比(后文简称载荷比)下轴承的载荷分布,结果如图6所示:1)仅受轴向载荷时,各钢球与沟道的接触载荷相同;2)随径向载荷增大,钢球最小接触载荷逐渐减小,径向载荷增大至500 N时,部分钢球的接触载荷极小(最小值为0.12 N)。
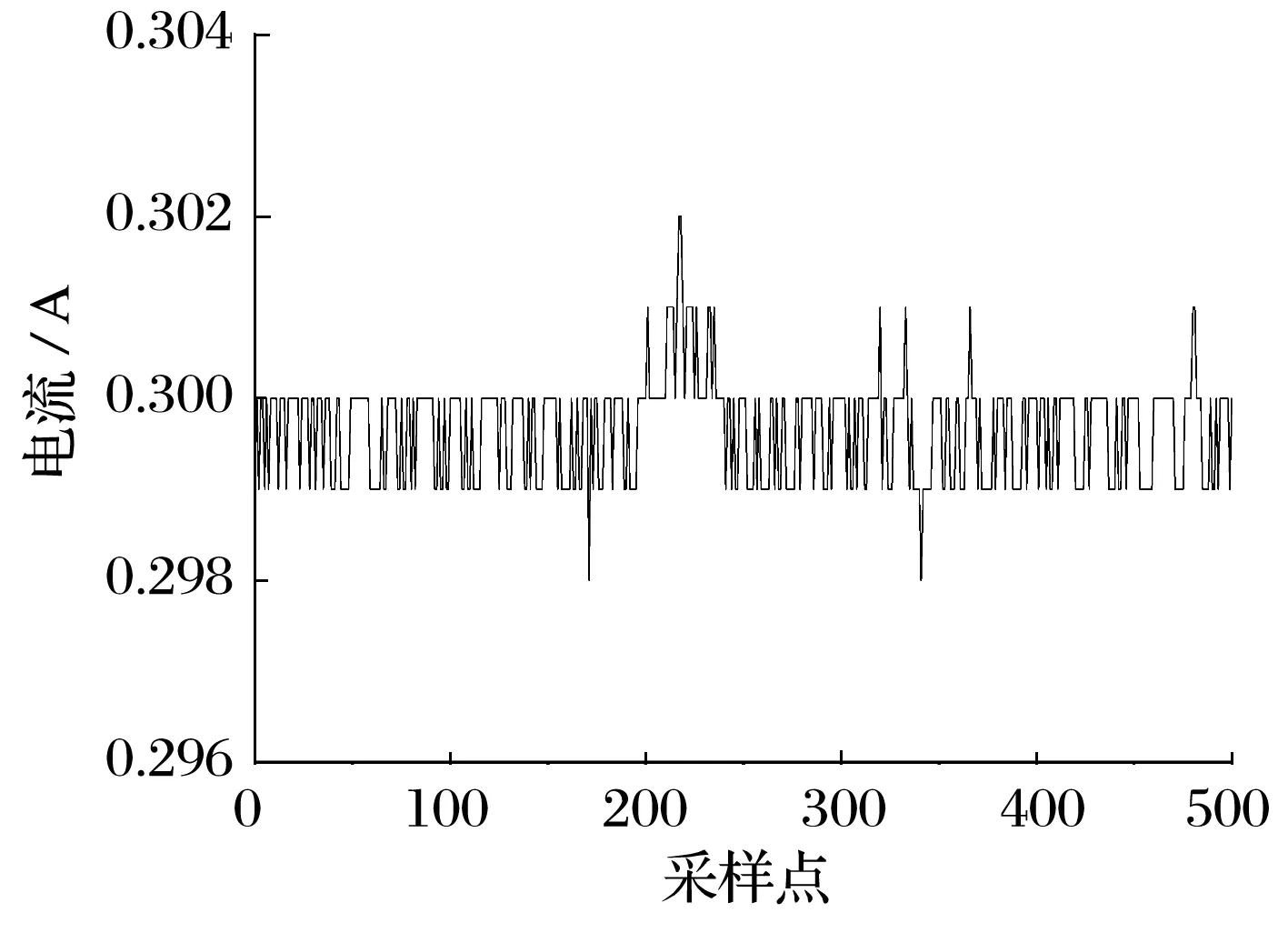
在接触载荷作用下,钢球与沟道之间存在摩擦力矩MF,当MF 图7 钢球无陀螺旋转时的载荷 考虑到精密轴系中实际轴向载荷不能过大,根据轴系典型工况条件Fr分别为100,200,300 N,取载荷比在0.5~4.0范围内仿真分析。不同载荷比下钢球相对内圈沟道的旋滚比(钢球绕接触面法线的自旋角速度与钢球相对于套圈沟道的滚动角速度的比值,旋滚比越大,钢球自旋滑动摩擦越大,钢球越易摩擦损伤)如图8所示:1)当载荷比较小时,3种径向载荷对应的钢球旋滚比均较小。2)随载荷比增大,Fr为100 N时钢球旋滚比快速增大;当Fr/Fa<2.0,Fr为200,300 N时钢球旋滚比缓慢增大;当Fr/Fa>2.0时,钢球旋滚比快速增大。 图8 载荷比对钢球旋滚比的影响 角接触球轴承摩擦力矩主要受载荷影响,包括钢球与套圈之间的弹性滞后引起的摩擦力矩、钢球的自旋滑动引起的摩擦力矩、钢球与沟道间差动滑动引起的摩擦力矩、钢球与保持架兜孔接触产生的摩擦力矩、保持架与套圈之间的摩擦力矩、润滑剂黏性摩擦力矩等,计算模型参考文献[10]。轴承摩擦力矩及其波动值随载荷比的变化如图9所示:1)当载荷比一定时,随径向载荷增大,轴承摩擦力矩增大,其波动值减小。2)随载荷比增大,轴承摩擦力矩减小,其波动值逐渐增大。 综上分析可知:当载荷比取1.25~2.00时,钢球不会发生陀螺打滑,钢球旋滚比较小,轴承摩擦力矩及其波动值较小,轴承综合性能较佳。 采用直流无刷电动机驱动精密轴系运转,如图10所示,驱动电压恒定,电流产生的电磁力矩与轴承摩擦力矩平衡,可通过电动机电流来间接反映轴承摩擦力矩及其波动[16]。 图10 直流无刷电动机驱动精密轴系 转速为5 000 r/min,径向载荷Fr为200 N时,取轴向载荷为50~200 N,不同载荷比下精密轴系的电流及其波动分别如图11和图12所示。 由图11可知:当载荷比为1.0时,电流均值较大,波动较小;随载荷比增大,电流均值减小但波动明显加剧。 由图12可知:随载荷比增大,电流均值减小,但其电流波动值增大。分析结果与仿真结果一致。 基于动力学理论建立了含一对角接触球轴承的精密轴系仿真分析模型,分析了径、轴向载荷比对轴承载荷分布、钢球旋滚比以及轴承摩擦力矩的影响,并通过试验验证了仿真结果的正确性,得到如下结论: 1)随载荷比增大,钢球最小接触载荷减小,载荷比小于4可以防止钢球发生陀螺打滑; 2)随载荷比增大,钢球旋滚比先缓慢增大后迅速增大,载荷比小于2.0有利于减轻轴承的自旋滑动; 3)随载荷比增大,轴承摩擦力矩减小,但其波动值增大。 (a)Fr/Fa=1.0 图12 载荷比对精密轴系电流均值及其波动的影响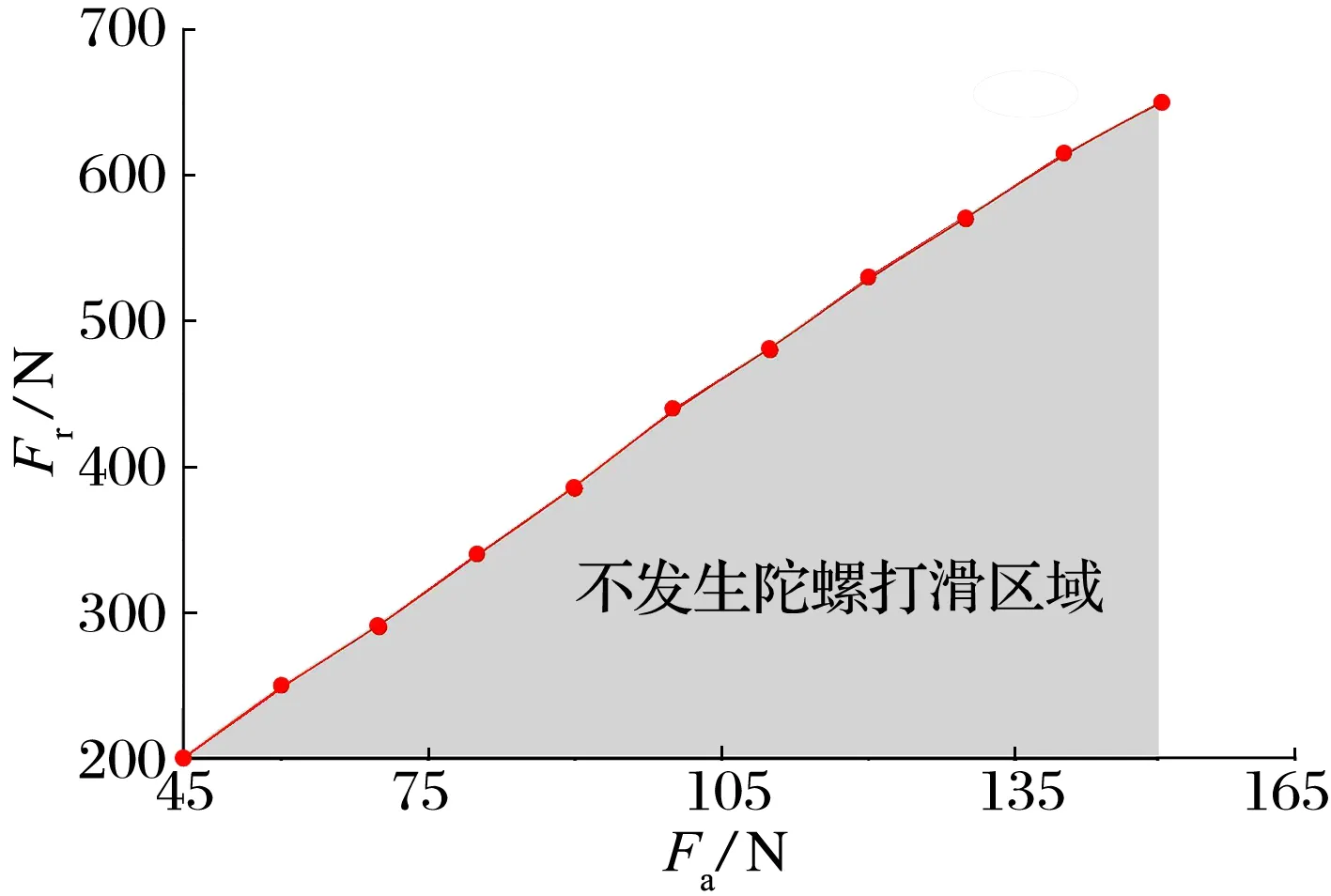
2.2 载荷比对钢球旋滚比的影响

2.3 载荷比对轴承摩擦力矩的影响

2.4 小结
3 试验验证

4 结论