主动磁悬浮轴承系统保护轴承碰撞特性研究

2022-06-22聂傲男李迎春夏维华邱明黄昆

轴承 2022年6期

聂傲男，李迎春,2，夏维华，邱明,2，黄昆

(1.河南科技大学机电工程学院，河南洛阳 471003；2.机械装备先进制造河南省协同创新中心，河南洛阳 471003；3.洛阳轴承研究所有限公司，河南洛阳 471039)

0 引言

主动磁悬浮轴承(Active Magnetic Bearing， AMB)系统广泛应用于风电、核能、航空航天等领域[1]，相比于传统转轴系统，磁悬浮轴承能够达到更高的转速，转动过程中不存在摩擦问题。保护轴承作为磁悬浮轴承系统的重要组成部分，对整个系统的安全十分重要。转子正常转动时，保护轴承内圈与转子不接触，当设备启停或发生故障导致浮力消失时，保护轴承起到临时支承的作用，保护设备的安全。

为提高保护轴承抗跌落性能和服役期间可靠性，有必要对转子跌落到保护轴承的过程进行动力学研究。文献[2]利用ADAMS，MATLAB和ANSYS联合仿真，建立车载飞轮电池中的磁悬浮转子系统动力学模型，与传统风力发电机的对比研究表明，该设计降低了风力发电机样机的启动阻力矩，验证了研究结果的可行性和有效性。文献[3]以垂直轴磁悬浮风力机的支承结构为研究对象，建立主轴结构跌落仿真模型，通过对比主轴的运动轨迹，直观展现出保护轴承结构对磁悬浮主轴跌落过程中运动轨迹的影响。文献[4]对磁悬浮转子系统进行受力分析，利用多体动力学软件对转子跌落到保护轴承过程中保护轴承所受的碰撞力进行仿真，分析转子偏心状态下跌落转速和动平衡精度等级对碰撞力的影响，结果表明随着跌落转速和动平衡精度等级的提高，保护轴承所受的轴向碰撞力保持不变，径向碰撞力随之增大。文献[5]提出使用弹性环来缓冲转子跌落所带来的冲击和振动，并针对2种不同的安装位置建立转子跌落的动力学模型进行数值仿真计算，结果表明将弹性环安装于转子上更能有效减小转子跌落后的振动幅度和冲击力。文献[6]对高速转子跌落在保护轴承上的碰撞力进行了理论分析和试验研究，并提出了转子跌落在保护轴承上的碰撞力测量方案，设计了碰撞力测量装置。文献[7]以HTR-10磁力轴承氦风机试验台架中的辅助轴承为研究对象，使用ABAQUS有限元软件数值模拟转子跌落，分析滚动辅助轴承内圈与滚动体的变形及能量损耗特性，并与初步的试验结果进行比对，验证了辅助轴承的可靠性。文献[8]对保护轴承的瞬态热响应进行了研究，对保护轴承的寿命预测有一定的参考价值。文献[9]求解了柔性转子跌落后的瞬态响应，在不同转子系统参数下，计算了支承阻尼对转子位移的影响，并将其与简单柔性转子模型的最佳支承阻尼进行比较，结果表明这种支承阻尼优化方法可用于确定磁悬浮轴承支承阻尼的最佳取值范围。

国内外学者对磁悬浮轴承系统进行了大量的研究，并取得了巨大的成果，但对磁悬浮轴承系统中的保护轴承研究较少，且对立式磁悬浮轴承系统及相关跌落试验的研究也很少。因此，本文以立式主动磁悬浮轴承系统为研究对象，建立转子跌落在保护轴承上的碰撞模型，利用ADAMS建立转子跌落过程的动力学模型，并基于上述模型研究不同初始速度、碰撞面摩擦因数对转子跌落过程的影响规律，通过立式转子跌落试验评价保护轴承的抗跌落性能。

1 立式主动磁悬浮轴承系统

1.1 立式主动磁悬浮轴承系统结构

立式主动磁悬浮轴承(以下简称磁悬浮轴承)系统结构如图1所示，上保护轴承为2套精度P4的满装71913C角接触球轴承，内外圈材料为GCr15轴承钢，球材料为Si3N4陶瓷，轴承采用面对面安装；下保护轴承为1套6014深沟球轴承。上保护轴承的轴向保护间隙为0.5 mm，径向保护间隙为0.2 mm，下保护轴承径向保护间隙为0.2 mm。当转子跌落时轴向冲击力完全由上保护轴承承担，因此本文重点研究上保护轴承。

1—下保护轴承；2—径向磁悬浮轴承；3—轴向磁悬浮轴承；4—径向磁悬浮轴承；5—电动机转子;6—电动机定子；7—上保护轴承；8—转速传感器；9—位移传感器；10—立式转子。

1.2 转子跌落在保护轴承上的碰撞模型

当轴向磁悬浮轴承失效后，转子做自由落体运动，同时具有很高的初始转速，转子和保护轴承内圈端面发生多次碰撞和回弹。转子跌落的轴向碰撞模型如图2所示，La为上保护轴承的轴向保护间隙，Lr为上保护轴承的径向保护间隙，d为上保护轴承内圈内径，d1为上保护轴承内圈挡边直径，Ka为保护轴承轴向支承刚度，Ca为保护轴承轴向阻尼。

图2 转子跌落的轴向碰撞模型Fig.2 Axial collision model during dropping of rotor

轴向碰撞力为

Fa=Kca(|za-zia|-La),

(1)

(2)

式中：Kca为转子与保护轴承内圈端面轴向碰撞刚度；za为转子轴向位移；zia为保护轴承内圈轴向位移。

假设碰撞面摩擦因数为μd，则轴向碰撞所产生的摩擦力矩[10]为

(3)

由于上保护轴承由2套角接触球轴承组成，为简化分析，将2套轴承作为一体分析，则轴承内圈在x，y，z方向的振动方程为

(4)

式中：mi为2套轴承内圈质量之和；Cr为轴承的径向支承阻尼；Kx，Ky，Kz为轴承在3个方向上的时变支承刚度；xi，yi，zi为轴承在3个方向上的位移；Fx，Fy，Fz为2套轴承的内圈当成一体时在3个坐标轴方向的受力。

转子跌落过程中的主要热源包括转子与保护轴承内圈端面之间轴向碰撞所产生的滑动摩擦生热和保护轴承转动所产生的热量。轴向碰撞产生的摩擦力矩可通过(3)式计算，保护轴承转动产生的摩擦力矩主要采用整体法计算，文献[11]提出了较为准确的计算方法，即

M=M1+MV,

(5)

M1=f1PDpw,

(6)

(7)

式中：M1为由外加载荷引起的摩擦力矩；MV为润滑剂黏性摩擦产生的力矩；f1为与轴承类型和载荷有关的系数；P为当量载荷；Dpw为球组节圆直径；f0为与轴承类型和润滑方式有关的系数；ν0为润滑剂的运动黏度；n为轴承转速。

碰撞面之间的滑动摩擦生热功率为

H1=1.047×10-4Mcan,

(8)

保护轴承转动所产生的发热功率为

H2=1.047×10-4Mn。

(9)

根据与碰撞面直接接触的各物体质量，可以假设滑动摩擦发热量的1/3传递到保护轴承上。设保护轴承内圈升速时间为t1，碰撞过程持续总时间为t2，则保护轴承端面由于滑动摩擦所产生的温升为

(10)

保护轴承转动所产生的温升为

(11)

式中：m为保护轴承的质量；c为轴承材料的比热容。

由于转子跌落过程属于高度非线性行为，为简化保护轴承温升的计算，提出了较多假设条件，只能根据物理学基本公式近似计算跌落过程中保护轴承的温升。

2 仿真分析

2.1 仿真模型的建立

使用仿真软件对轴承进行分析已经很常见，但对于转子跌落过程的动力学仿真还相对较少。对于长时间或多次跌落的仿真，ADAMS更具优势[4]，因此本文采用ADAMS对转子和保护轴承进行仿真研究。

根据试验机的相关参数，利用ADAMS建立立式磁悬浮轴承系统转子跌落过程的动力学仿真模型如图3所示。上调整垫的作用是保护转子，不同直径的调整垫可满足不同型号保护轴承的使用，上调整垫与上保护轴承内圈内径之间存在0.2 mm的径向保护间隙。上垫片与上保护轴承内圈端面之间的距离等于轴向保护间隙0.5 mm，由其他零件(如上端盖等，已省略)将上垫片和转子连为一体，跌落时与保护轴承内圈端面发生碰撞。因研究重点为转子跌落对保护轴承产生的碰撞过程，该模型进行了简化处理，省略了电动机、径向磁悬浮轴承、轴向磁悬浮轴承等零件，并用一个空心圆柱体替代下保护轴承。

图3 简化的立式磁悬浮系统动力学仿真模型

设置各零件的材料类型，转子质量设为45 kg。将2套上保护轴承外圈设为固定副，为更加符合实际跌落情况，不对转子施加旋转副约束，仅给定转子的初始转速和竖直向下的重力加速度，使旋转的转子在重力作用下自由跌落。根据物体间的运动关系，采用Impact冲击函数法设置合适的接触关系，具体接触参数见表1。

表1 仿真模型接触副参数设置

整个仿真模型共有固定副6个，接触副149个。选取转子初始转速和碰撞面摩擦因数为分析对象，根据工程实际中转子正常工作转速以及轴承端面的表面粗糙度，确定转子跌落时初始转速研究范围为0～30 000 r/min，摩擦因数为0.050～0.200。由于仿真模型涉及接触副较多，计算量大，为提高计算效率，将求解时长设置为0.4 s，歩数为4 000步。求解完成后利用后处理器提取转子轴心轨迹、碰撞力等数据。

2.2 结果与分析

2.2.1 跌落过程的动力学响应

为研究转子跌落后的动力学特性，以初始转速20 000 r/min、摩擦因数0.075、径向保护间隙0.2 mm、轴向保护间隙0.5 mm等作为输入边界条件，对转子的运动状态进行分析。

转子在20 000 r/min初始转速下跌落0.4 s内，在径向平面内的质心轨迹如图4所示。转子质心的轴向位移随时间的变化趋势如图5所示。

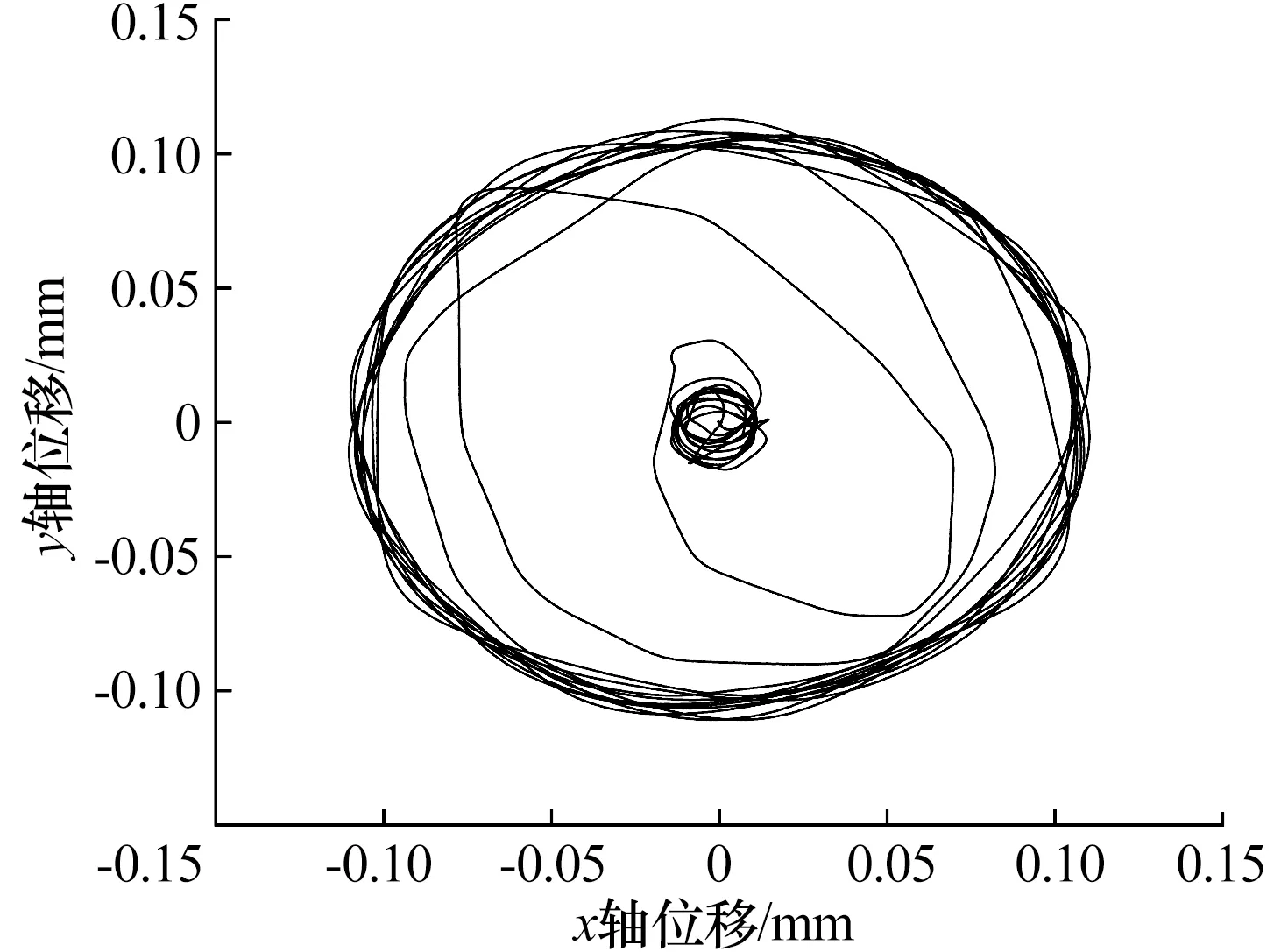
图4 径向平面内转子质心轨迹Fig.4 Centroid trajectory of rotor in radial plane

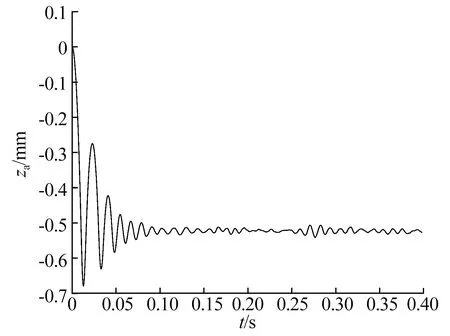
图5 转子质心的轴向位移Fig.5 Axial displacement of rotor centroid

由图4可知，转子在径向平面内作近似圆周运动，说明转子跌落过程中的运动相对稳定，并没有发生反向涡动[12]。

由图5可知，转子质心轴向位移随跌落时间的变化呈多次跌落和回弹，且每次回弹高度逐渐减小，并最终趋于稳定，这是由于转子跌落过程中与保护轴承内圈发生碰撞和滑动摩擦引起能量损失。当跌落时间为0.01 s时，转子质心的轴向位移为0.50 mm，等于轴向保护间隙，说明此时转子跌落到保护轴承内圈上并发生接触；转子在经历0.013 s的跌落运动和接触变形后首次发生回弹，此时转子质心的轴向位移(0.68 mm)最大；从0.10 s左右开始，转子的跌落回弹运动趋于稳定，轴向位移稳定于约0.52 mm处。转子每次跌落的轴向位移均大于轴向保护间隙0.5 mm，且转子稳定后的轴向位移比轴向保护间隙大了约0.02 mm，这是由于转子跌落到保护轴承内圈端面后保护轴承受碰撞力的影响而产生一定变形量，当转子回弹趋于稳定后，又受转子自身重力的影响而发生变形，并随着时间推移逐渐减小。

研究跌落过程中产生的碰撞力对评估保护轴承损伤状况和抗冲击性能具有重要意义，立式转子跌落过程中与保护轴承内圈端面之间的轴向碰撞力Fa和径向碰撞力Fr随时间t的变化趋势如图6所示。

由图6a可知:在0.01 s时立式转子与保护轴承内圈端面首次碰撞，这与图5所示的两者首次发生接触的时间一致，最大轴向碰撞力 (3 217 N)也在此时产生；由于每次碰撞均会损失一部分机械能，因此轴向碰撞力逐渐减弱，最终在转子重力441 N(45 kg)附近波动。

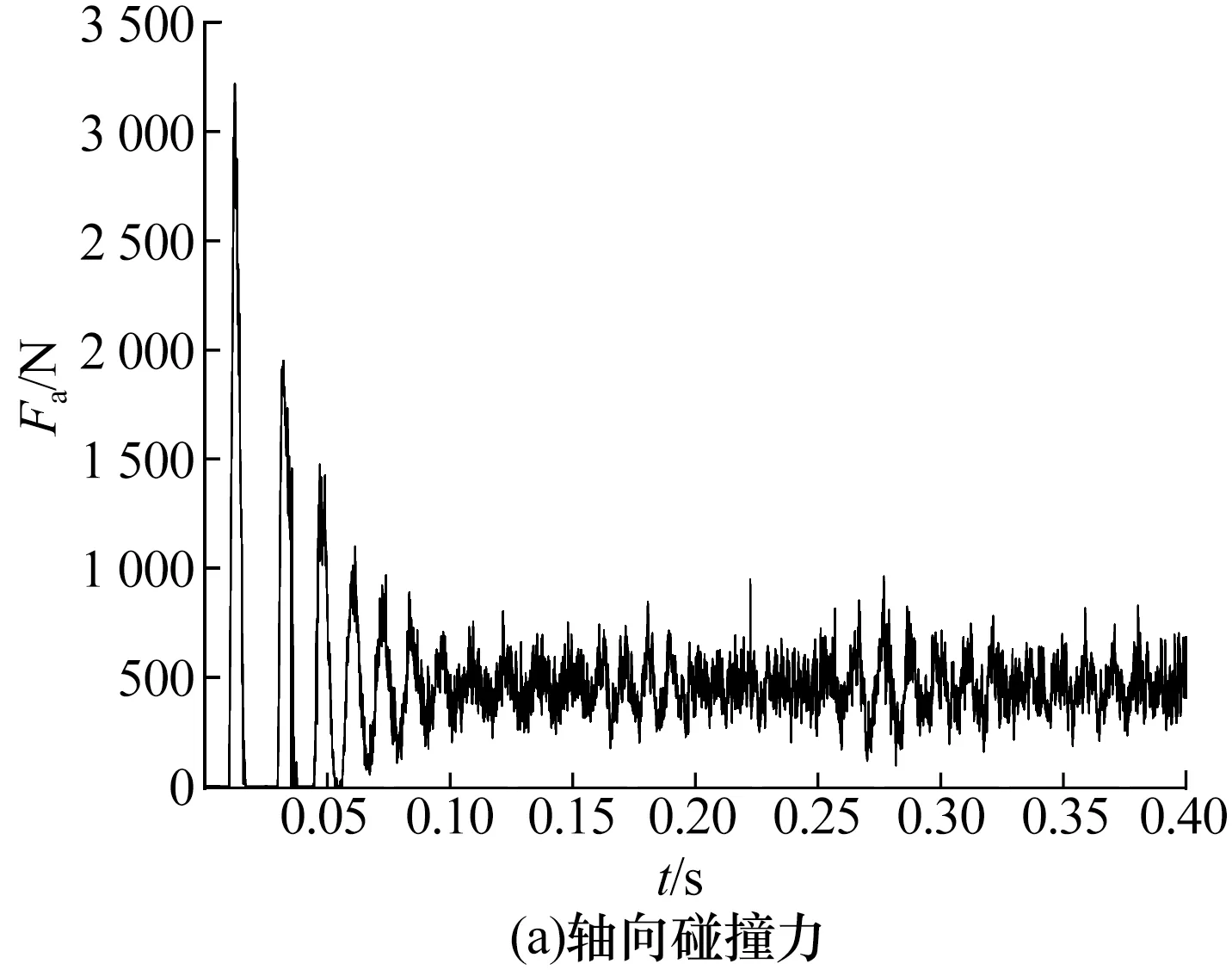
由图6b可知:最大径向碰撞力并未出现在首次碰撞，相比于轴向碰撞力随着转子跌落和弹跳运动呈现出明显的规律性和周期性，径向碰撞力的随机性很大，这是由于立式转子与保护轴承内圈端面的碰撞属于高度非线性行为，转子与保护轴承内圈初始速度相差很大且在接触表面发生了相对滑动，转子受到保护轴承内圈摩擦力矩的影响，在径向平面内作近似圆周运动(图4)，并与保护轴承内圈发生随机碰撞。

2.2.2 初始转速对最大碰撞力和保护轴承最大接触应力的影响

选取不同初始转速，其他边界条件(摩擦因数0.075、径向保护间隙0.2 mm、轴向保护间隙0.5 mm)保持不变，研究立式转子跌落初始转速对转子跌落的最大碰撞力和保护轴承最大接触应力的影响。

最大轴向和径向碰撞力随初始转速的变化规律如图7所示，不同初始转速下，保护轴承球与沟道之间的最大接触应力如图8所示。

图7 初始转速对最大碰撞力的影响Fig.7 Influence of initial speed on maximum collision force

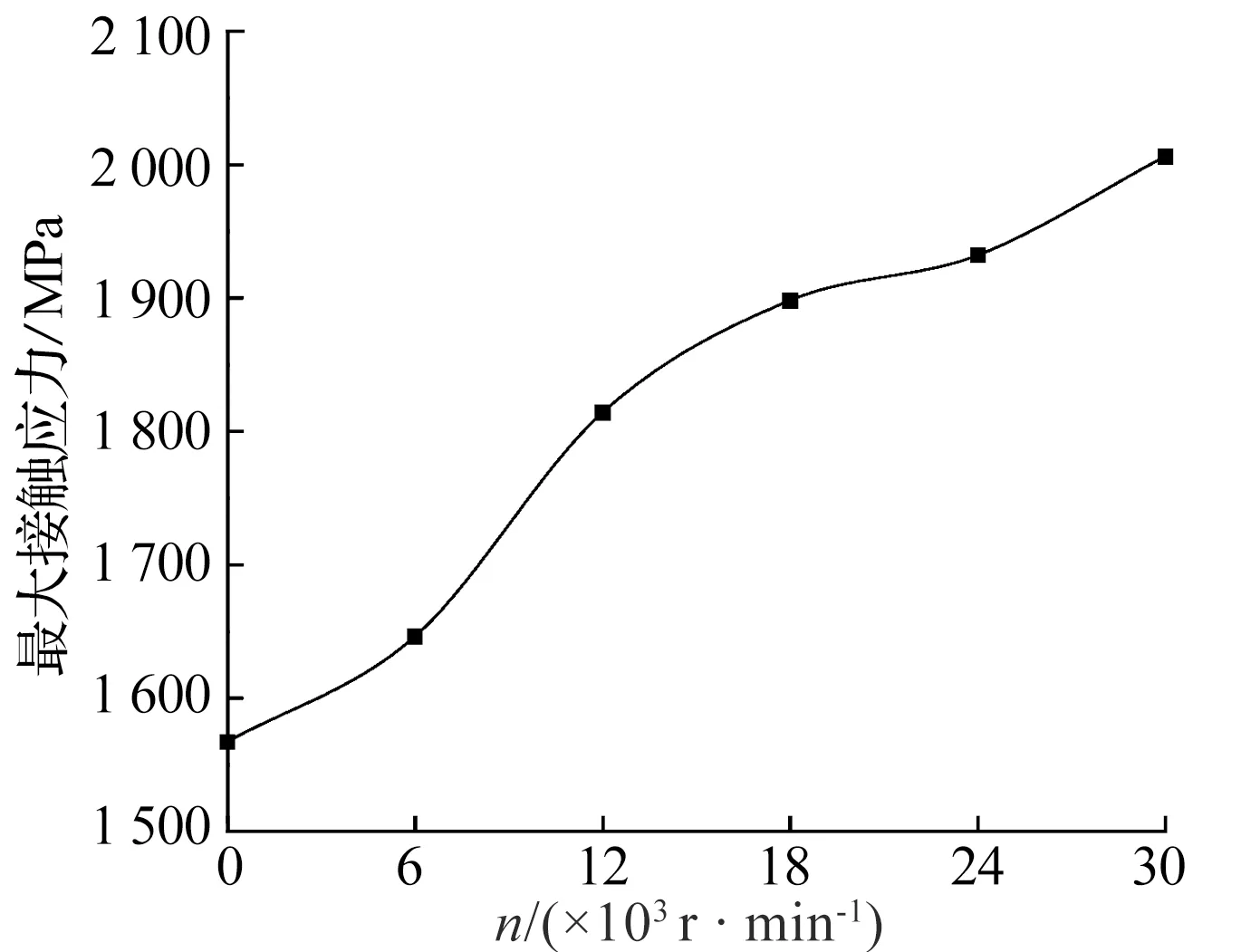
图8 初始转速对最大接触应力的影响Fig.8 Influence of initial speed on maximum contact stress

由图7可知，随着转子初始转速从0增加至30 000 r/min，最大径向碰撞力从0增加至2 344 N，而最大轴向碰撞力基本不变，约为2 800～3 000 N。这是因为转子的重力和跌落高度(轴向保护间隙)决定了转子所具有的动能和势能，其值越大则轴向碰撞力越大；而径向碰撞力与转子在径向平面内的运动情况有关，转子的初始转速越高，与保护轴承内圈端面接触时所产生的滑动越强烈，摩擦力矩越大，转子在径向保护间隙内的涡动现象也就越明显，最大径向碰撞力也越大。因此，增加初始转速对最大轴向碰撞力几乎无影响，而最大径向碰撞力则越来越大。另外，当转子以零初始转速跌落时不存在径向平面内的摩擦力矩，跌落过程中的最大径向碰撞力始终为零，仅存在轴向碰撞力。

由图8可知，随着立式转子初始转速的增大，保护轴承球与沟道之间的最大接触应力也越来越大。这是由于初始转速的增大使保护轴承所受合力增大，根据赫兹接触理论计算的接触应力也随之增大。当初始转速高达30 000 r/min 时，最大接触应力仅为2 006 MPa，远低于轴承钢的许用应力，从接触应力角度来看，该保护轴承完全能够承受转子跌落带来的冲击载荷。

2.2.3 摩擦因数对最大碰撞力和保护轴承最大接触应力的影响

碰撞面之间的摩擦因数对转子跌落的最大碰撞力和滑动摩擦也有很大影响，为探究碰撞面摩擦因数对最大碰撞力和最大接触应力的影响，设边界条件为：初始转速24 000 r/min、径向保护间隙0.2 mm、轴向保护间隙0.5 mm、非碰撞接触副摩擦因数0.075保持不变。

碰撞面摩擦因数对最大轴向和径向碰撞力的影响规律如图9所示，不同碰撞面摩擦因数下，保护轴承球与沟道之间的最大接触应力如图10所示。

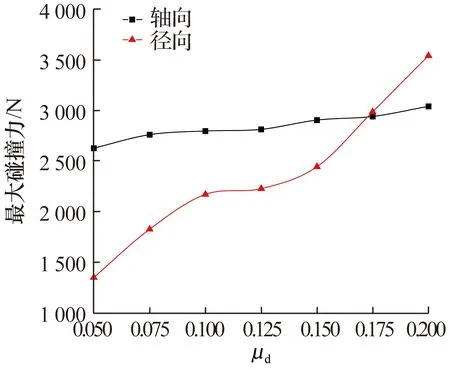
图9 碰撞面摩擦因数对最大碰撞力的影响

由图9可知：随着碰撞面摩擦因数的增大，最大轴向碰撞力基本不变，而最大径向碰撞力随之增大。原因与初始转速类似，增大碰撞面摩擦因数使径向平面内的滑动摩擦加剧，因此径向碰撞力随之增大，而对轴向碰撞力影响不大。另外，随着碰撞面摩擦因数的增大，最大径向碰撞力逐渐接近最大轴向碰撞力并最终反超。

由图10可知，保护轴承球与沟道之间的最大接触应力随着碰撞面摩擦因数的增大而增大，但最大接触应力仅为2 440 MPa，并未超过许用应力。

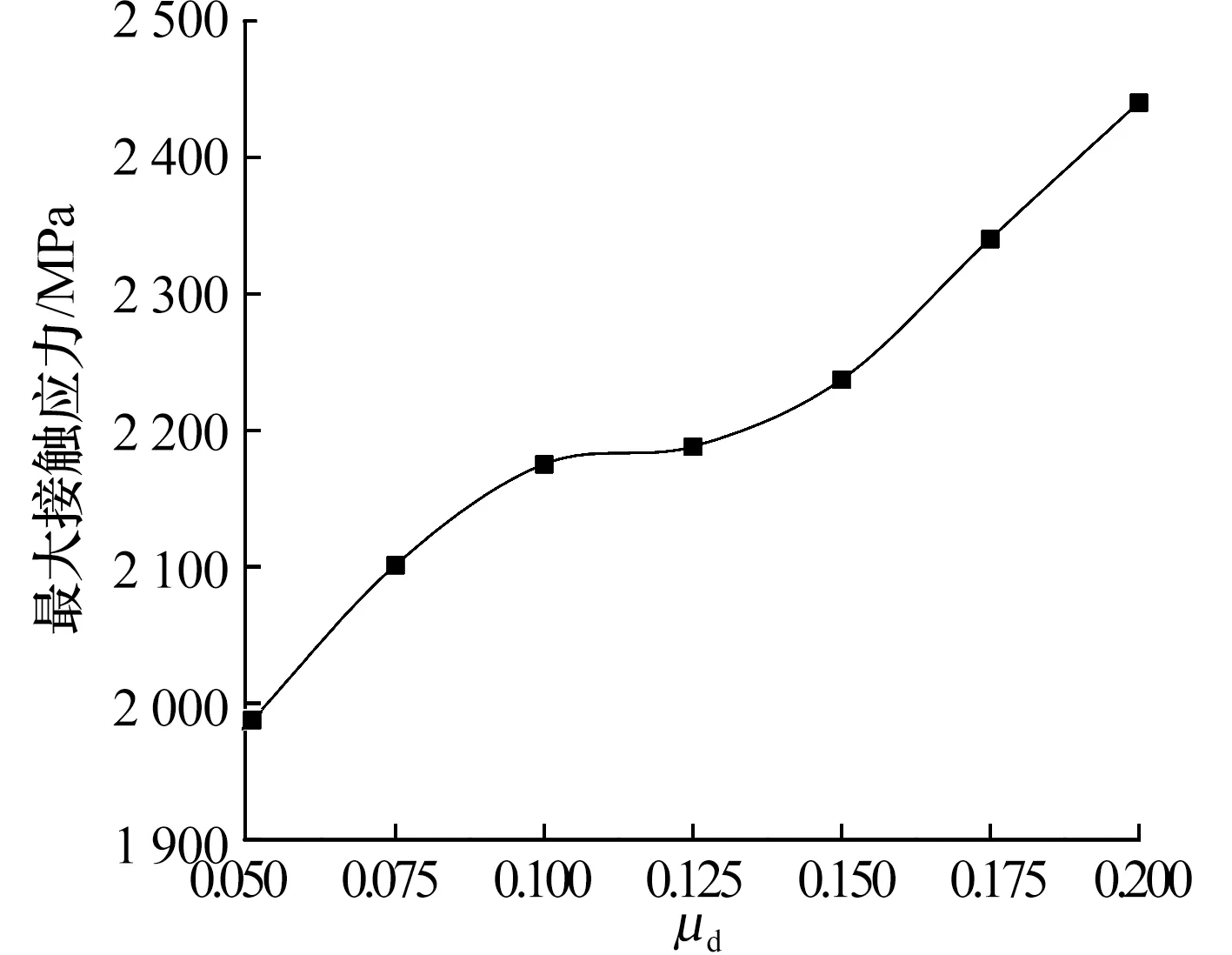
图10 碰撞面摩擦因数对最大接触应力的影响

3 转子跌落试验

为评价保护轴承的抗跌落性能，采用图11所示的磁悬浮轴承系统保护轴承寿命试验机进行了立式转子跌落试验。该试验机主要由试验机主体、电磁轴承控制系统、试验监控系统、冷却系统和辅助设备等组成，能够模拟立式磁悬浮轴承系统转子跌落到保护轴承的工况，评价跌落后保护轴承的损伤情况，并实时监测跌落过程中的主轴转速、保护轴承温升等指标。

图11 磁悬浮轴承系统保护轴承寿命试验机

本次跌落试验条件为：初始转速20 000 r/min、径向保护间隙0.2 mm、轴向保护间隙0.5 mm、转子质量45 kg，保护轴承为成对71913C角接触球轴承。

跌落试验中传感器采集到的转子转速和上端面温度随时间的变化曲线如图12所示，转子转速在跌落70 s内减小为零，上端面温度由15.1 ℃上升至34.8 ℃。这是由于转子在跌落过程中与保护轴承内圈之间的碰撞和滑动摩擦使转子损失动能，导致转子转速逐渐减小，而损失的能量转化为大量摩擦热，使系统温度升高。热传导需要一定的时间，因此在跌落后大约14 s时转子上端面的温度才开始上升。另外由于转子转速太高，从安全角度考虑试验机采用的是非接触式温度传感器，而空气的热传导系数远小于金属，使转子上端面温度测量值比实际值小。

图12 转子转速和上端面温度随时间的变化曲线

由于上保护轴承由2套角接触球轴承面对面组成，为方便区分，从上到下依次记为1#上保护轴承(与碰撞面接触)和2#上保护轴承。跌落试验后1#上保护轴承和上调整垫外观如图13所示：直接受到冲击碰撞的1#保护轴承内圈小端面呈暗蓝色，沟道内润滑脂完全蒸发，说明碰撞面之间的滑动摩擦热使内圈小端面严重烧伤;上调整垫外径表面1#保护轴承位置处的滑动摩擦痕迹比2#位置更加明显，说明靠近碰撞面的1#保护轴承的工况更恶劣。

图13 跌落试验后1#上保护轴承和上调整垫外观

通过检测跌落试验后保护轴承内圈端面的硬度，可以反推试验过程中内圈的最高温度。跌落试验后上保护轴承内圈端面硬度和估计温度见表2，硬度为同一端面任意3个测量点的平均值。由表2可知：1#保护轴承小端面硬度最低，估计温度高达680 ℃；2套保护轴承大端面之间的硬度相差很小，估计温度均为270 ℃；2#保护轴承小端面硬度最高，为61.0 HRC，没有发生烧伤现象；硬度和估计温度从上到下分别呈现出梯度递增和递减的趋势，说明碰撞面之间的滑动摩擦是最大发热源。

表2 试验后上保护轴承内圈端面硬度和温度

以试验跌落工况为输入参数，根据碰撞模型和温升计算公式求得碰撞面滑动摩擦引起保护轴承的温升为375.1 ℃，跌落过程中保护轴承转动造成的温升为266.4 ℃。保护轴承转动造成的温升加上环境温度15.0 ℃即281.4 ℃，可近似认为是2套保护轴承内圈接触区域大端面的温度；保护轴承转动造成的温升和滑动摩擦生热引起的温升再加上环境温度即656.5 ℃，可认为是直接受到冲击碰撞的1#保护轴承内圈小端面的温度。温度理论计算与试验结果相差23.5 ℃，相对误差仅为3.5%。

综上可知：导致保护轴承失效的最主要原因是碰撞面间的滑动摩擦，大量摩擦热使保护轴承内圈急剧升温，端面烧伤严重，沟道内润滑脂完全蒸发；但保护轴承仍然承受住了转子跌落带来的破坏，对磁悬浮轴承系统起到了保护作用。

为应对跌落过程中产生的摩擦热带来的不利影响，提高保护轴承的抗跌落性能，可对保护轴承进行表面处理，如对保护轴承端面进行精磨甚至抛光，或者在保护轴承端面、沟道等关键表面上沉积一层具有耐高温、自润滑功能的固体润滑膜等，以改善其表面粗糙度，降低碰撞面滑动摩擦生热，进而提高保护轴承抗跌落性能和使用寿命。