铷原子自旋噪声谱分析中的窗口效应实验研究
2022-06-22孔嘉汪孟珂伏吉庆刘浩陆晓铭
孔嘉,汪孟珂,,伏吉庆,刘浩,,陆晓铭
(1.杭州电子科技大学 理学院,杭州 310018;2.中国计量科学研究院 磁参量计量实验室,北京 100029)
磁场精密测量技术具有十分重要的研究价值,被广泛应用于生物医学[1]、军事侦察技术[2]、地球物理学[3]和工业检测[4]等领域.先进的磁场测量方法和高性能的磁传感器一直是世界各国重点研究领域.得益于现代原子物理和激光领域的快速发展,磁场的精密测量技术也得到了突飞猛进的发展[5-7].原子磁力计是一种测量碱金属原子蒸气在磁场中的拉莫尔进动来对微弱磁场进行测量的仪器,其灵敏度可以与超导量子干涉仪[8]相媲美,而且在体积和成本上具有可小型化的优势.在原子磁力计走向极致时,需要对其自身的量子噪声,例如原子自旋噪声开展研究,才有可能进一步突破标准量子极限,提升测量灵敏度.自旋噪声(Spin Noise)[9]是指热平衡态自旋的随机热涨落.由于自旋噪声非常微弱,不仅难以被探测到,还很容易被各种噪声淹没,使得信号分析面临巨大的挑战.在量子精密测量中,有不同的信号分析方法来应对不同种类的信号和噪声问题.例如,可以进行多次测量求平均[10]来减小恒定信号的测量误差;再如,可以用贝叶斯信号恢复方法[11]来有效追迹随时间演化的信号;此外,频谱分析可以降低宽频噪声对特定频率信号的影响,使得本来在时域上难于显现的信号在频域上清晰显现出来.频谱分析不仅在工程噪声分析上有广泛的应用,在量子精密测量,比如量子噪声分析[12]、量子干涉仪[13]、原子磁力计[14]等装置中也有不可取代的地位.在原子系综量子噪声研究中,自旋噪声谱是近年来新兴的一种研究方法,不仅可以进行噪声分析,还可以实现系统参数的标定.
自旋噪声谱(Spin Noise Spectroscopy,SNS)[15]是一种测量自旋在探测光传播方向上投影涨落的光学技术.通过探测系统在非激发条件下的自旋涨落,可以揭示系统在热平衡状态下的性质.自旋噪声谱借助频谱分析的方法中的快速傅里叶变换(Fast Fourier Transform,FFT)来对传感器采集的时域信号转换到频域上.在转换时有许多参数选择会对频域信号产生影响.例如,采样率、采样时间、带宽、窗口函数等.在大多数量子精密测量的频谱分析中只关注功率谱的相对值,比如压缩度只涉及相干态和压缩态噪声的比值,而并不关注噪声本身大小的绝对值,那么此时窗口函数的选择就对结果没有影响.因而这也造成了窗函数在数据处理时非常容易被忽视的现象.原子磁力计中的大部分噪声分析、参数标定也都不需要频域信号的绝对值大小.比如噪声分析时,常常只关注系统噪声、光子学噪声、电子学噪声之间的比值.而当需要对磁场信号实时追踪时,需要首先通过原子自旋噪声谱来对系统的参数进行可靠的校准,而这时候如果忽略窗口效应,就会得到不符合实际的参数大小,导致磁场估计偏差较大.
本文将系统地研究快速傅里叶变换过程中,窗口效应在自旋噪声谱进行系统参数标定时会产生的影响,并给出实验上的修正关系.这将为后续利用自旋噪声谱对原子系综进行标定和分析提供便利的修正方案.
1 傅里叶变换中的窗口效应
理论上,用快速傅里叶变换测量信号的频率成分时,假定了时域信号时间长度是无限的,或者测量的信号是周期性的.然而在实际应用时,测量的信号大多是非周期的,而且对信号的观测时间有限,相当于截取了信号的一部分.这就导致采样信号首尾不连续,在快速傅立叶变换后表现为原始信号中不存在的高频分量,似乎一个频率的能量会泄漏到其他频率.这种现象被称为频谱泄漏[16],它会导致精细的谱线扩展成更宽的信号.因此直接对信号进行快速傅里叶变换会产生频谱泄露、导致频谱失真.为了减小频谱泄漏对信号的影响,通常使用窗口函数对输入的时域信号加窗,再对加窗后的信号执行FFT,以获得更为准确的频谱曲线.
窗函数是由一个主瓣和多个小幅值的旁瓣组成的连续频谱.主瓣位于时域信号的每个频率分量的中心,旁瓣接近零.旁瓣的高度则表示窗函数对主瓣周围频率的影响.在实际应用中,选取窗函数需要注意主瓣和旁瓣的幅值与展宽两个参数,较高而窄的主瓣能够提高分辨率,幅值较低的旁瓣能够减小频谱泄露.但通常窗函数难以同时满足这两点,当主瓣宽度较窄时,旁瓣幅值较高,频谱泄漏较严重﹔当旁瓣幅度较小时会使主瓣频率范围展宽.每个窗函数都有自己的功能特点,适合不同的应用,应当根据被分析信号的频率性质来选择合适的窗函数.
一般情况下,不额外加窗与使用矩形窗(Rectangle)在幅值和能量上结果是一样的.因而在对数据进行快速傅里叶变换时,默认使用矩形窗对信号进行截取.特点是主瓣集中,旁瓣较高,会使变换中带进高频干扰和泄漏.不考虑信号幅值精度,只关注精确的频率,可选用矩形窗,例如测量物体的振动频率.汉宁窗(Hanning),又称升余弦窗.函数表达式为W(n)=0.5(1-cos(2πn/N)),0≤n≤N,窗口长度L=N+1.其窗旁瓣显著减小,在两端都为逐渐减少到零,消除了所有的时域信号不连续性,频谱泄漏被消除的很好.但其主瓣加宽,频率分辨力下降.汉宁窗口可以满足大部分应用的需求[17].如果测试信号有多个频率分量,频谱表现较为复杂,就可以选择汉宁窗.海明窗(Hamming),也叫作汉明窗,函数表达式为W(n)=0.54-0.46cos(2πn/N),0≤n≤N.海明窗与汉宁窗都是余弦窗,只是加权系数不同,使旁瓣达到更小.但其旁瓣衰减速度较慢,因此信号中仍然有轻微的不连续性,在抵消最近的旁瓣方面做得更好.布莱克曼窗(Blackman),是二阶升余弦窗,函数表达式为W(n)=0.42-0.5cos(2πn/(L-1))+0.08cos(4πn/(L-1)),0≤n≤M-1,其中,M=N/2,当N为偶数;M=(N+1)/2,当N为奇数.所得频谱具有宽峰值,但旁瓣压缩良好.等效噪声带宽比汉宁窗要大一点,波动小一点.频率识别精度最低,但幅值识别精度最高,有更好的选择性.常用来检测两个频率相近幅度不同的信号.平顶窗(Flattop)在频域有非常小的通带波动,比其他窗口更接近信号的真实幅度.由于在幅度上有较小的误差,所以这个窗可以用在校准上.平顶窗的函数表达式为W(n)=a0-a1cos(2πn/(L-1))+a2cos(4πn/(L-1))-a3cos(6πn/(L-1))+a4cos(8πn/(L-1)),0≤n≤L-1.其中参数a0=0.215 578 950;a1=0.416 631 580;a2=0.277 263 158;a3=0.083 578 947;a4=0.006 947 368.
加窗计算通常会衰减原始时域信号的幅值与能量,因此对于最后的结果还需要加上修正系数[18],不同窗口函数的修正系数不同.理论上讲,修正系数应使加窗后幅值与同样长度的矩形窗相等.从实验数据出发来标定铷原子自旋噪声谱中窗函数的修正系数
K=A/A′,
(1)
其中,A和A′分别为不加窗(或矩形窗)和加窗后测得的信号大小.
2 自旋噪声谱实验
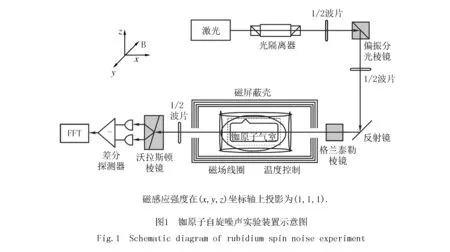
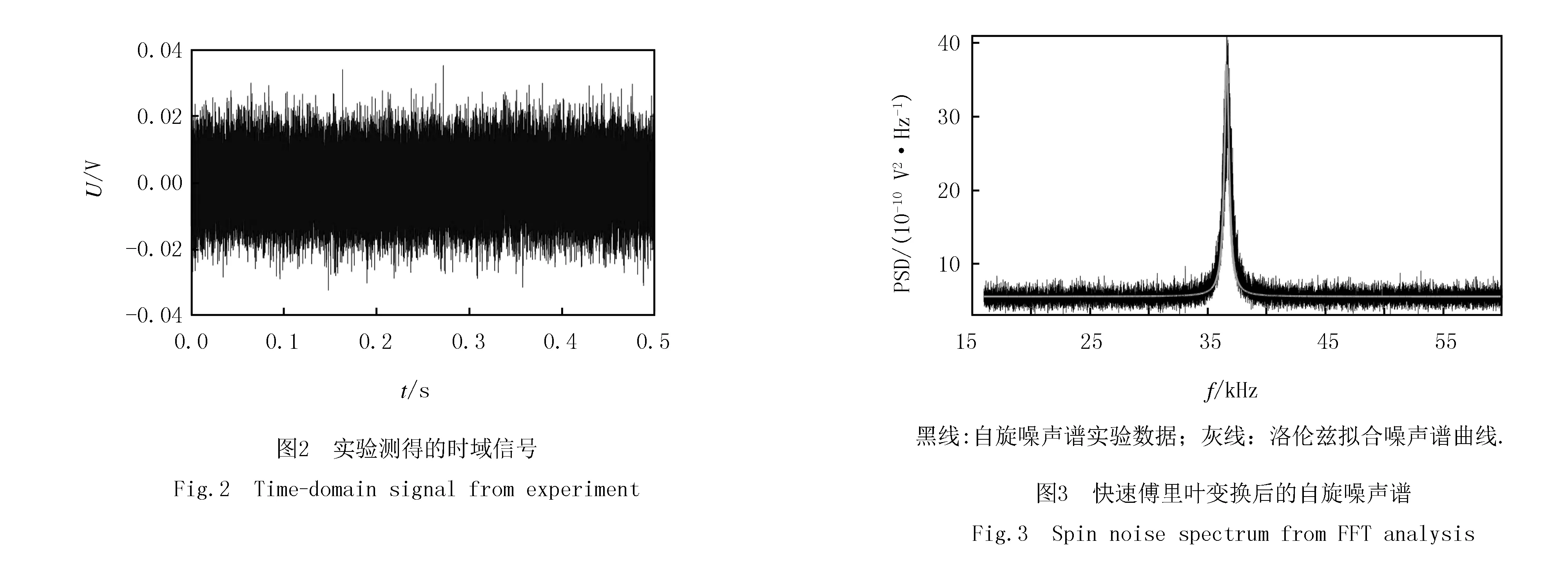
铷原子自旋噪声实验装置如图1所示,主要包括探测光源、原子气室控温装置、磁场控制线圈以及自旋噪声信号探测系统.在控制探测光功率等其他实验参数不变的情况下,将原子气室的温度从59 ℃逐步升高到110 ℃,在稳态时测量原子气室的自旋噪声谱,观察温度对自旋噪声信号的影响.在不加窗的情况下进行快速傅里叶变换,并对频谱信号进行洛伦兹线型拟合,得到自旋噪声谱的幅值、线宽、信噪比等信息.以探测光功率3 mW,温度为100 ℃时测量结果为例,给出了时域信号如图2所示.
傅里叶变换后的自旋噪声谱如图3所示,其中灰线为采用洛伦兹函数对数据进行拟合后结果.拟合方法为洛伦兹曲线拟合,拟合表达式
(2)
其中,参数y0是噪声基底,A是信号幅值,ν0是信号中心频率,γ是信号半峰全宽(Full Width Half Maximum,FWHM).为探究铷原子自旋噪声信号中的窗口效应与修正关系,在3 mW光功率条件下,采集了不同温度下的自旋噪声信号,并对每一组数据采用不同窗函数来进行数据处理.
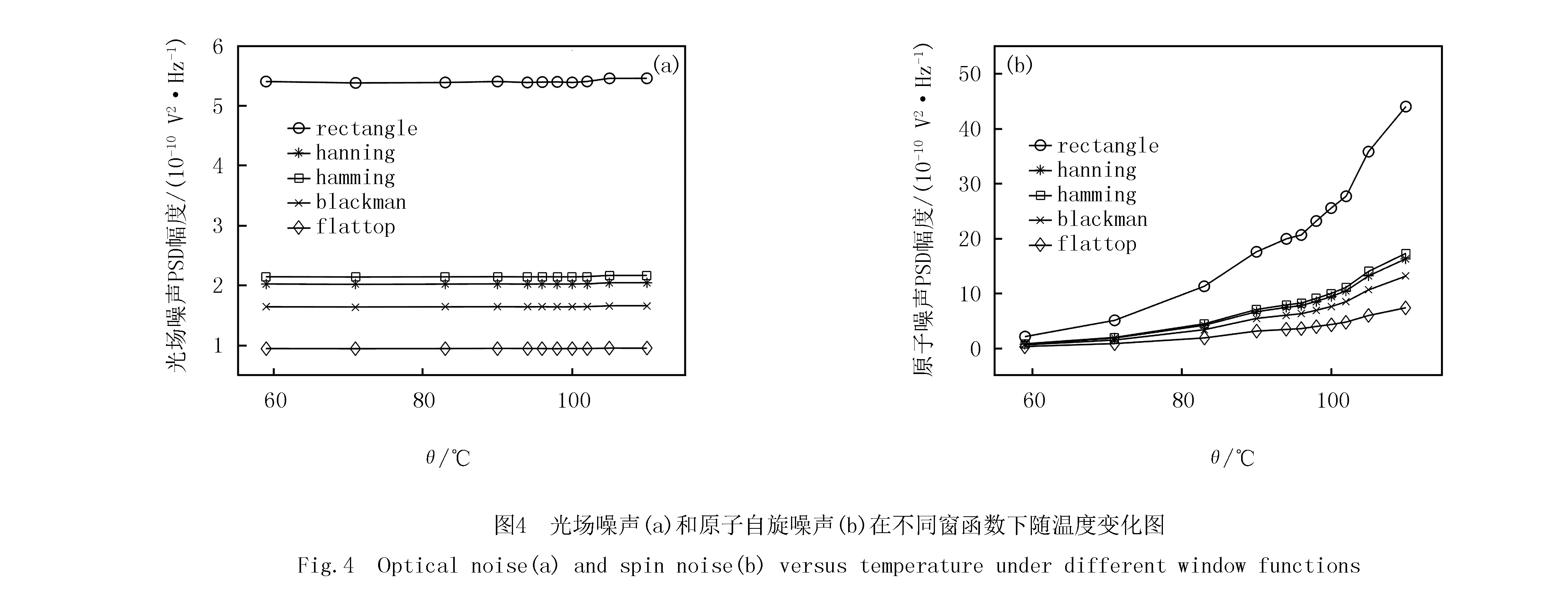
添加窗函数拟合后,光场噪声和原子噪声大小如图4所示.随着温度的增加,光场噪声几乎没有变化,说明光场噪声不受温度影响.原子噪声幅值随温度有明显变化,温度越高时,原子噪声幅值信号越强.对比不同窗函数选择下的结果,发现加窗对光场噪声和原子噪声幅值确实有衰减,且不同的窗口函数衰减因子不同.
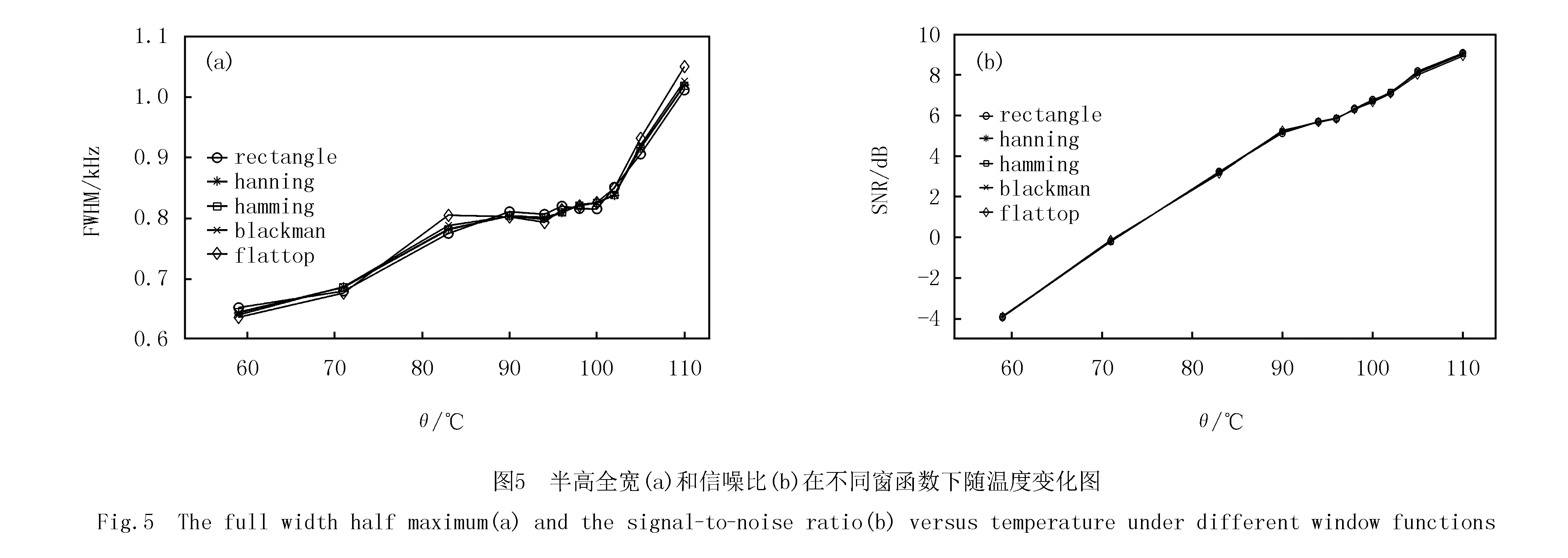
如图5所示,对加窗前后的FWHM和信噪比(Signal-to-Noise Ratio,SNR)对比结果发现,加窗对信号线宽和信噪比几乎没有影响.FWHM标定了原子系综的相干寿命,SNR标定了光与原子相互作用的耦合强度.从分析结果来看,这两个参数的拟合可以在任意窗函数情况下来完成,且不需要修正.
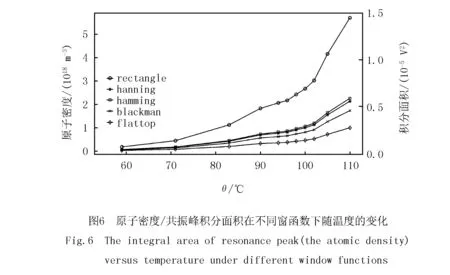
自旋噪声谱中共振峰下的积分面积也会给出原子系综中的重要信息,比如原子密度.光学深度较大的情况下,原子密度很难用原子吸收谱的方法来标定.这时自旋噪声谱就是一个很好的方法.在一些量子噪声分析和磁场信号追踪的研究中,原子密度标定的准确性会直接影响测试结果.对自旋噪声谱的积分面积进行了测量和分析,发现它强烈依赖于窗函数的选择.如图6所示,若不对窗口效应进行修正将得到错误的原子密度估计.
3 窗口效应修正关系
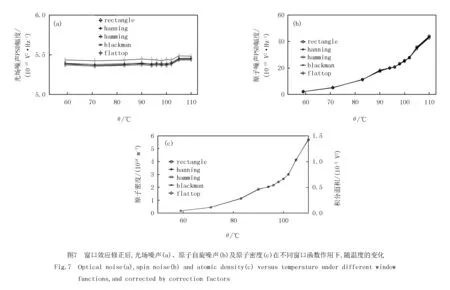
根据以上实验数据和方程1 的定义,测得了铷原子自旋噪声谱信号在不同窗口函数条件下的修复系数.修正系数分别为:hanning,2.67;hamming,2.51;blackman,3.28;flattop,5.75.将这组修正系数应用到铷原子自旋噪声谱分析中,如图7所示,可以看出各个参数在不同窗口下的表现基本都恢复到同一水平,且与矩形窗(即不加窗口函数)时的表现一致.尤其是对积分面积的修复较好,可以方便地测得系统在不同温度下对应的原子密度值.
4 结 论
本文以铷原子气室的自旋噪声谱为例,对快速傅里叶变换中窗函数选择带来的谱线变化进行了分析.在59 ℃到110 ℃的原子温度情况下,采集得到原子自旋在恒定磁场作用下的自旋噪声信号.通过快速傅里叶变换的方法得到自旋噪声谱后进行了洛伦兹线性拟合,以得到各参数的标定结果.在光功率等实验参数不变的情况下,可以看出温度越高,原子数密度越高,原子自旋信号幅度越大,信噪比越好,但线宽更宽,相干寿命变短.这一变化趋势不随频谱分析以及窗函数选择而改变.同时线宽(原子相干寿命)和信噪比(噪声相对值大小)也不受窗函数选择的影响,可以在任意窗函数下进行标定.而噪声的绝对值,和噪声谱积分面积的大小受窗函数选择的影响较大.给出了实验上的修正系数:hanning,2.67;hamming,2.51;blackman,3.28;flattop,5.75.修正后能够恢复信号幅值,不同窗函数恢复结果大致相同.这展示了数据处理时会引入的潜在人为误差,也解决了在利用自旋噪声谱进行原子密度估计时,常常会因数据处理导致密度不唯一的问题,也为密度估计提供了便利的修复系数.