T形结构中的熵随机共振

段正路，段守惠,樊碧璇

(江西师范大学 物理与通信电子学院,南昌 330022 )

随机共振(Stochastic resonance,SR)是指在非线性系统中，噪声(随机干扰)对系统输出信号增强的一类现象.1981年BENZI等人[1]借助气候双稳态模型合理地解释了地球古气候周期性变迁的难题，并在此基础上提出随机共振这一概念[2].此后，关于SR的研究多集中于双稳态系统[3-7]，其中，包括一些实验验证.1983年，FAUVE和HESLOT首次在实验上，通过交流电路的SCHMITT触发器证实了随机共振现象[6]. 1988年，美国佐治亚理工大学MCNAMARA,WIESENFELD和ROY等人[7]在环形激光器中发现随机共振现象.之后，微观动力学系统以及生物微结构中的随机共振引起了一定的关注[8-12].其中，2008年BURADA等人研究了布朗粒子在双腔结构中的运动，发现体系的熵势对其中的SR现象存在明显的影响，并由此提出熵随机共振[11].2010年GHOSH等人在BURADA的基础上提出双腔系统中的几何随机共振概念[12].双腔系统中的SR对微小结构中的粒子，如细胞、纳米小颗粒等的输运，筛选与分离具有重要意义，因此激起了具有对称双腔结构SR现象的研究兴趣.然而，微观动力学系统中的SR可存在于多种几何结构体系中，如三腔系统[13]，甚至更复杂的多腔系统.尽管已有研究者提出了单稳态[14]、三稳态[15]以及多稳态[16]的SR理论，但三腔或多腔系统的随机共振却少有研究.

受以上研究背景的启发，基于单稳态SR理论工作[14]，以及粒子在长通道中受熵势影响的扩散现象[17]，本文研究了布朗粒子在一种新颖而简单的T形腔室中的运动，并出于对布朗粒子在横向不再具备双稳、以及多稳态形式的受迫运动的好奇，参考双腔熵随机共振系统[11]，对T形腔中运动的布朗粒子施加一个横向周期驱动以及一个纵向外力，利用朗之万方程建立数值化模型，发现了T形腔室中的熵随机共振现象.

1 理论模型

布朗粒子在漏斗状T形结构中的运动，与ZWANZIG在文献[17]中描述的粒子运动问题很相似，差别是此处用的是一个封闭的T形腔室，而不是开放的管状通道，且研究的是粒子的受迫运动，而不是自由扩散.对二维T形结构中的布朗粒子施加横向周期驱动F(t)，以及一个纵向力G，可以建立图1所示模型，结构中底部两侧边界向外倾斜，其斜率的大小满足k=d/(xL-L).为了描述的简便，可将T形腔室的底部结构称为阱，阱两侧的边界称为阱侧壁.

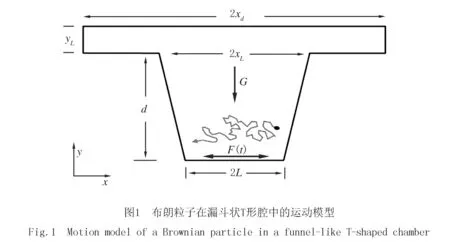
对图1结构中布朗粒子的过阻尼运动，可以借助无量纲化朗之万方程

(1)

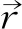
获得多粒子轨迹沿x方向的平均结果,

本文使用MATLAB软件，在程序中用条件语句对T形结构边界进行如下描述

约束粒子的运动范围.要求粒子只能在T形结构内部运动，本文采用反射边界条件.

(2)

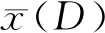
2 纵向力G引起的熵随机共振

经典双腔熵随机共振(Entropic stochastic resonance,ESR)要求一个额外的纵向力G作用在系统中的布朗粒子上.这是经典双腔ESR与几何随机共振之间的一个显著差别.为此，首先探究T形结构中纵向力G对体系共振的影响.通过对比图2(a)与(b)，可以发现漏斗状T形系统中，纵向力G对体系表现出随机共振现象至关重要，即使T形结构阱侧壁的斜率远大于1，在没有纵向力G，即G=0时，体系依然不能呈现出SR现象.

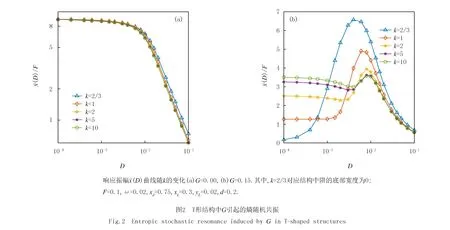
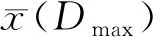
由于图2(b)显示的随机共振严格要求纵向力G的存在，且与结构关联密切，而系统结构又可沿周期力F(t)在横向等效为熵势，根据文献[11]这种随机共振现象可视为熵随机共振.

漏斗状T形结构中熵势的引入过程可以参考文献[17,20]，在此引入其中的一些关键步骤.对外部场中粒子的自由扩散，引入如下二维Smoluchowski方程

(3)

其中，P(x,y,t)为粒子的概率密度分布，V(x,y)表示粒子所处的能量势.在T形结构中G存在的情况下，V(x,y)可视为Gy.对(3)式进行积分，可以得到

(4)

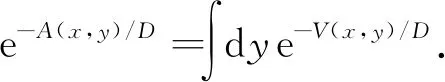
其中，势函数A(x)即为熵势的理论形式.在G存在的情况下，其满足如下形式

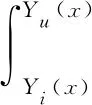
(5)

其中，Yu(x),Yi(x)分别对应结构的上边界和下边界.仅考虑T形结构中阱的等效熵势，可以将(5)式化为

(6)

在图3(a)中，漏斗状T形结构中阱等效的熵势表现出明显的几何依赖性，并且，改变T形结构中阱的斜率，并没有影响熵势的高度.在没有纵向力G时，横向的熵势变化并不能引起体系的随机共振(图2(a)).引入的纵向力G后，结构等效的熵势获得了明显增强(图3(b)).由文献[17]可知T形结构或其他结构中纯粹的熵势高低不表示粒子自由能的大小，仅表示结构对粒子扩散的一种阻碍.在将粒子的二维运动等效为一维运动的过程中，可将这种阻碍认为是熵势对粒子扩散的减缓.

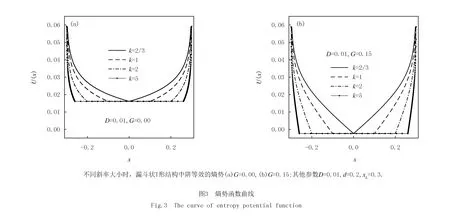
在漏斗状T形腔中，没有纵向力G时，结构的阻碍并不足以引起体系的随机共振；而引入的纵向力G与体系的内部几何产生关联，增强了结构对粒子响应F(t)的阻碍，导致体系呈现出了随机共振.因此，根据文献[11]，也可以理解为G对系统熵势的增强，并导致了体系的熵随机共振.

3 结 论

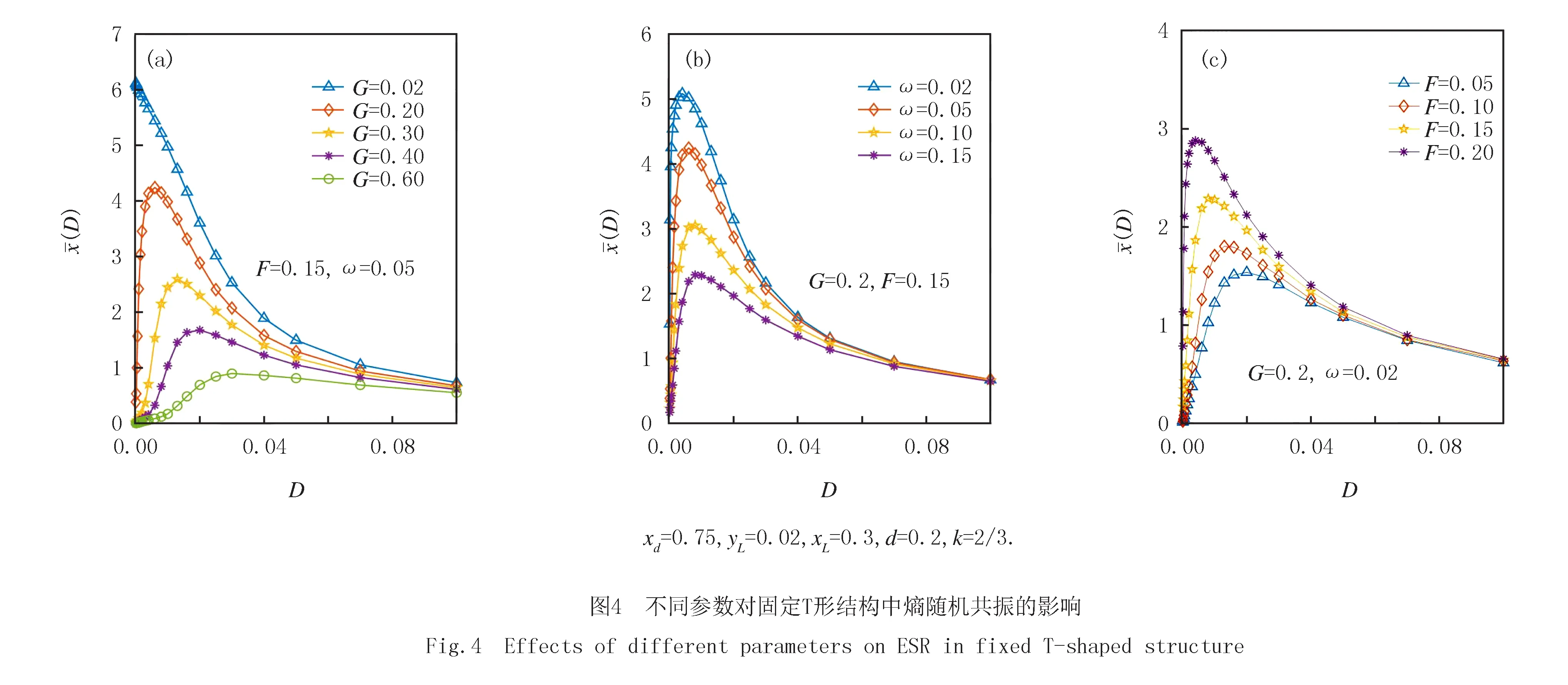
文章主要探究了受迫运动的布朗粒子在漏斗状T形结构中的熵随机共振现象.在没有纵向力G的情况下，漏斗状T形系统中无随机共振现象.然而，在体系中引入G之后，可以观察到明显的熵随机共振现象.改变G，周期驱动，以及体系结构，对系统中的SR现象都有明显的影响.结合纵向力引起的能量势以及体系结构引起的熵势，揭示了体系中的熵随机共振产生的机制. T形结构是一种典型的简单结构，在其中发现熵随机共振对不同微观体系中随机共振的研究都有参考意义，尤其在实际应用中可以为微观粒子，如细胞、生物大分子、纳米小颗粒等在狭长通道中的输运，筛选与分离提供参考.