二维水动力模型在无资料河段水位流量关系分析中的应用

宋 雄，李大成，马 黎，赵 乔

(中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081)

0 引 言

准确拟定河道设计断面水位流量关系对工程设计及水文监测都十分重要。一般来说，河道某一设计断面的水位可以通过布设水位站进行实时监测。目前，压力式、雷达式、气泡式等水位计已经广泛应用于江河湖泊水位的实时遥测，但目前行业仍未解决河道实时流量的有效监测。传统水文站流量测验方法是通过架设缆道，在施测断面上采用流速仪测取一些垂线的平均流速，并结合大断面测量成果加权平均求得断面平均流量。随着测流技术进步，声学多普勒流速剖面仪(ADCP)已被广泛应用于河道流量测验工作[1-4]。无论是采用流速仪还是ADCP都只能对河道进行间歇性测流，仍未解决河道流量实时遥测的问题。因此，率定出设计断面的水位流量关系，通过实时水位观测数据推算流量是获取河道不同时刻流量的主要途径。

对于工程设计，需要关注设计断面的水位流量关系，用于防洪、发电、供水、航运等设计。以水电工程为例，发电厂房尾水水位流量关系不仅关系到发电厂房的防洪安全、水轮机组的安装高程，还影响电站的发电水头，事关工程经济性。在水电站设计方案比选初期，设计河段通常没有实测水位流量关系点，不少工程，特别是国际工程推进速度很快，无法等到积累一定水位流量关系点据之后再进行方案设计。推求无资料河段设计断面水位流量关系是工程方案设计阶段的一项重要工作。

水利水电工程水文计算规范[5]5.3.4指出：“设计断面所在河段无实测水文资料时，可利用水文调查资料，在设计断面所在河段施测大断面、调查测量不同水位级的水面比降、临时观测水位、施测流量等，用多种方法推算水位流量关系，相互检验，合理确定。”但一些河段地理位置偏僻，甚至无法调查到历史洪水，难以按规范要求推求无资料河段的水位流量关系。

目前，关于无资料河段水位流量关系的研究较少，主要集中于一维水力学模型领域。茹伏高[6]根据设计断面大断面数据、河段河床比降、参照河床比降及区域水文站资料的洪水期水面比降、参照区域水文站的糙率资料的断面糙率，采用曼宁公式绘制了无资料河段水位流量关系曲线。陈瑞祥等[7]针对传统方法研究水位流量关系时忽略了河道洪水涨落、水流不稳定性等因素的影响，基于天然河道一维水动力学方程-圣维南方程及曼宁公式，提出稳定流比降与附加比降的计算方法，建立洪水涨落情况下的水位流量关系理论计算公式。周艏[8]针对传统比降面积法的不足，通过对滩槽合成法、动量输送法的应用对比，认为动量输送法更适合于无资料河段的水位流量关系定线。袁帅等[9]为解决无资料流域水文控制断面难以进行水位流量关系曲线经验拟合的现状，提出了一种以圣维南方程为理论基础的推导方法，推导出恒定流情况下的单一水位流量关系曲线。梅立庚[10]在无实测资料、无高水实测资料或冲淤变化影响水位流量关系时，假定设计断面下游起始断面水位，采用一维恒定非均匀渐变流计算方法推算设计断面水位流量关系。徐俊[11]指出，在国外工程设计中，有时要求根据HEC-RAS软件计算河道水面线后，推求出所需断面的水位流量关系。武金慧、刘娜[12]基于HEC-RAS一维模型计算了位于萨莫拉河上的厄瓜多尔某水电工程厂址水位流量关系。

本文尝试采用二维水动力模型分析计算设计断面的水位流量关系，并与传统一维水动力模型计算成果进行对比分析，以验证二维水动力模型对于水力特征较为复杂的河道水位流量关系拟定的适应性和可靠性。

1 基本原理

对于完全没有水文监测资料的河段设计断面，曼宁公式作为经典的水力学计算公式，因结构简单、计算准确而广泛应用于明渠水力计算。曼宁公式为

Q=AR2/3n-1J1/2

(1)

R=A/χ

(2)

式中，Q为河道流量；n为河道设计断面糙率；J为河道水力坡降；R为水力半径；A为过水断面面积；χ为湿周。

从曼宁公式的基础结构可以看到，河道设计断面的糙率及河道水力坡降的取值直接影响到设计断面水位流量关系的计算精度。一般来说，河道设计断面糙率可以根据河道河槽类型及情况参考经验进行取值，但是河道水力坡降的取值在天然河道中随意性较大。这主要体现在计算坡降时，需选取设计断面上下游一定长度河段进行计算，选取的随意性一般较大，不同的人计算的河段水力坡降差异可能巨大。

采用一维水力学模型进行设计断面水位流量关系的推求，在一定程度上缓解了采用曼宁公式直接求取单一断面水位流量关系时坡降难以确定的尴尬，但计算精度与计算模型采用的断面数量密切相关。一般来说，采用更密集河道横断面的一维模型，计算精度会更高。

本文主要研究采用二维水力学模型计算设计断面水位流量关系的方法，二维水动力学模型主要计算原理是建立河流流态的质量和动量平衡方程。具体如下：

流态质量平衡方程

(3)

流态的能量平衡方程

(4)

(5)

式中，Z为河道断面水位，m；H为断面水深，m；v为不同方向的流速，m3/s；g为重力加速度，m/s2；n为断面糙率；u为摩阻流速，m3/s，采用以下方程计算

(6)

式中，u*为横向流速，m3/s；v*为侧向流速，m3/s；Cf为摩阻比。

本文以位于非洲地区的一段天然河道为例，结合HEC-RAS软件建立研究河段二维水力学模型，通过求解上述方程组，计算水流在研究河段不同计算网格单元间的运动情况，最终提取出设计断面的水位流量关系，并与传统一维水力学模型计算成果进行对比，分析二维水力学模型在水位流量关系计算上的可能，为无资料河段水位流量关系的计算提供另一种思路。

2 方法应用

2.1 研究河段概况

研究河段位于非洲的卢阿拉巴河上游，研究河段长约0.8 km，河段蜿蜒曲折，存在多处洼地回水区域，河段河床为卵石块石、两岸分布有较大块石，河段水流较急，两岸常年淹水线以上为阔叶林及大型灌木。

研究河段存在多处断面突变，形成了天然的局部“鱼肚”水塘(见图1)，水流在此种河段流态极为复核，采用传统的曼宁公式及一维模型分析断面水位流量关系精度欠佳。

图1 研究河段地形

2.2 一维计算模型

2.2.1 断面布置

根据设计断面所处位置，选取长约800 m的河段作为计算河段，河段最下游断面远离设计段面，沿河段共布设50个断面，平均断面间距为16.4 m，断面布设密度较高，尽可能的反映河段河道形状。一维计算模型的断面布置见图2。本文选取的设计断面编号为990、2200及2513，最下游断面编号为8；990号断面代表了局部顺直河段的典型断面，2200号及2513号断面作为鱼肚型水塘中复杂水流条件下的代表断面。

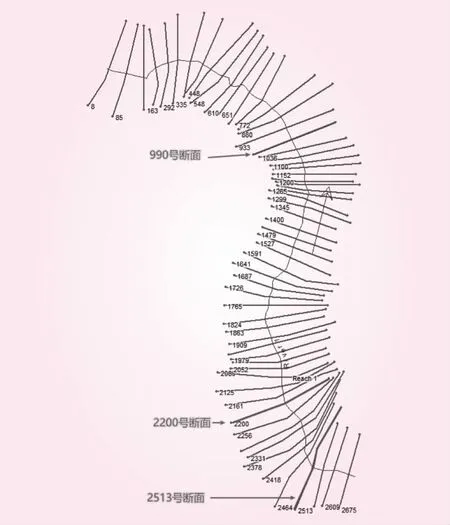
图2 一维计算模型断面布置平面

选定计算河段下游边界时，充分考虑了设计断面与下游边界断面间的河段河道形状，尽量使设计断面与下游边界断面间的河道具有一定的水力控制能力，本次选择的下游边界8号断面与第一个设计断面990号断面间不仅存在河道弯道控制，且断面448号～707号间的河段较为束窄，易形成河段河槽水力控制，使得下游边界断面水位流量关系发生变化时，不会对设计断面的水位流量关系造成大的影响。

2.2.2 参数及边界条件

本文采用一维恒定流计算设计断面的水位流量关系。一维计算模型的主要设置参数为下游边界条件及河道断面糙率。由于计算河段下游末端已经处于宽缓河段，且下游边界远离所选设计断面，可采用正常水深作为下游边界条件；结合河段天然状况参考糙率取值表，所有河道横断面糙率取一综合值0.06。

上游边界选取36个恒定流量作为入流，流量范围为5～1 500 m3/s，流量级可较好覆盖河段多年来流量范围。

2.2.3 计算成果提取

采用一维恒定流分别计算上述36个流量下的河段水面线，并提取出设计断面相应的水位流量关系(见图3)。

图3 不同流量级河段水面线计算成果

2.3 二维计算模型

2.3.1 模拟范围与计算网格生成

(1)模拟范围。二维计算模型的模拟范围与一维计算河段基本保持一致。范围边界位于计算流量淹没线范围以上。

(2)计算网格。计算网格需要充分反映河段地形变化情况，计算网格过密会导致二维模型计算时间过久，过于稀松，又无法反应河段真实地形，特别是水力坡降发生剧烈变化的区域。分析结果显示，研究河段主河道平均宽度60 m左右。最终决定将计算网格边长取为5 m，同时在设计断面处通过设置断裂线加密优化计算网格。二维计算模型模拟范围及优化后的计算网格见图4、5。

图4 二维计算模型分析范围及计算网格生成

2.3.2 参数及边界条件

二维计算模型的边界条件与一维计算模型较为类似，主要包括上下游开边界的设置及二维模拟区域的糙率设置。具体如下：

(1)上游边界。采用人工生成的非恒定流量过程线(见表1)作为上游边界的入流过程，该入流过程从0线性增加至1 160 m3/s，此后又线性减小至0。需要说明的是，侧重研究设计断面的水位流量关系时，入流过程无需采用实测洪水过程，只需使流量过程覆盖关注的设计流量级即可。

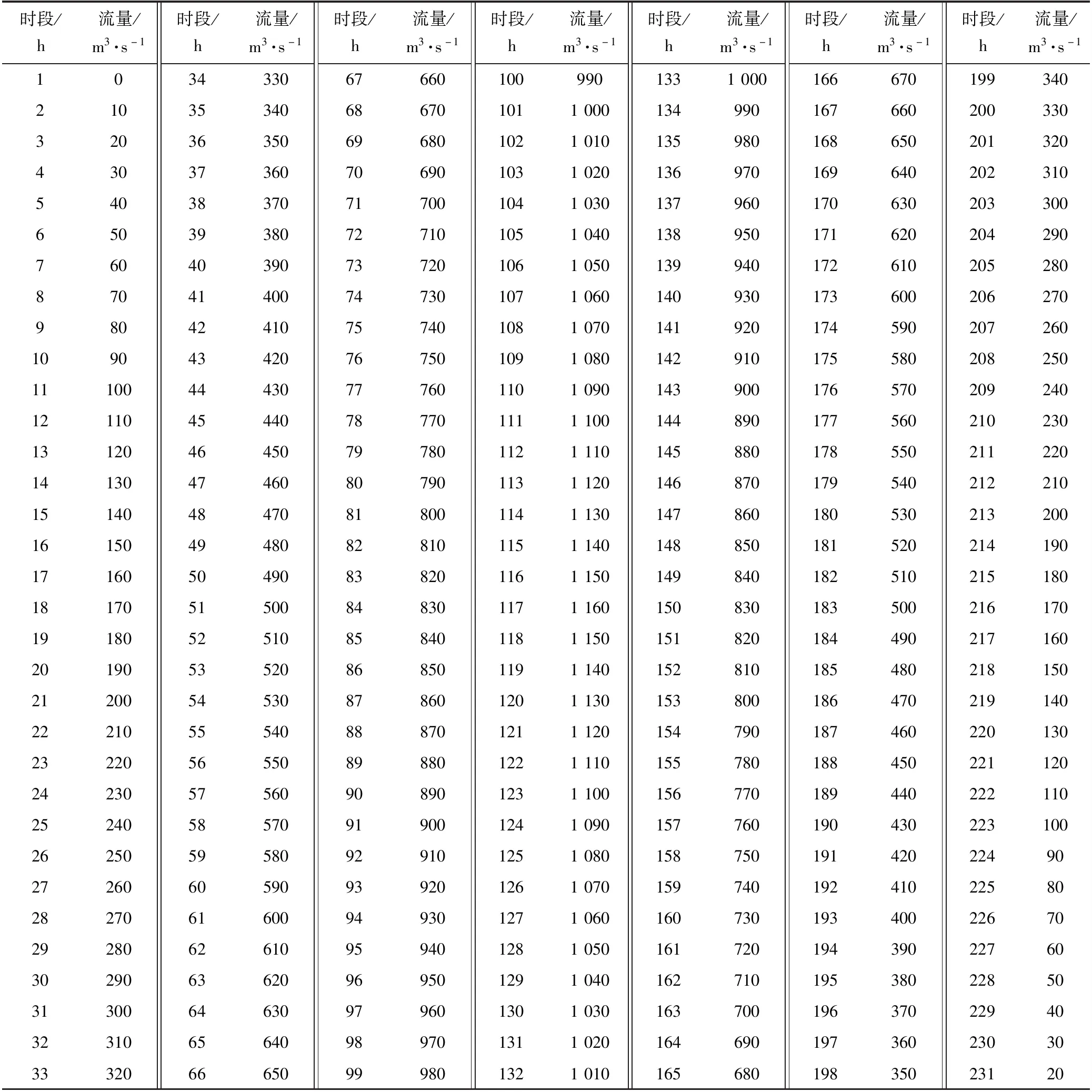
表1 二维计算模型上游边界入流过程

(2)下游边界。下游边界条件设定与一维计算模型保持一致，即采用正常水深作为下游边界条件。

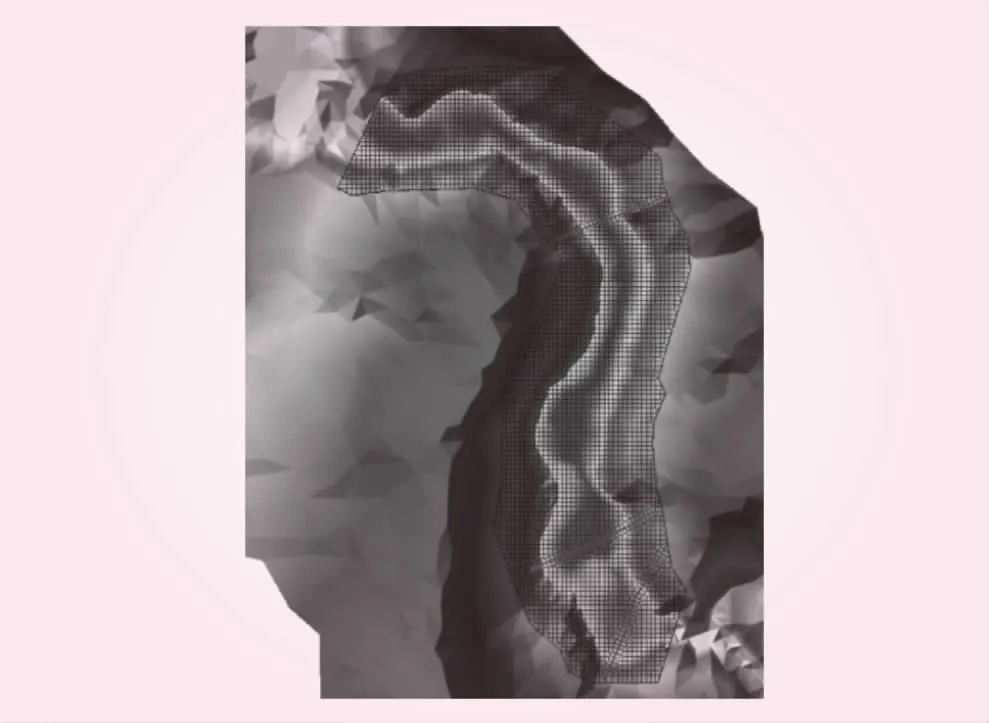
图5 二维计算模型计算成果展示

(3)糙率。二维计算区域内的糙率与一维断面糙率保持一致，取一综合糙率0.06，便于与一维计算模型进行成果比较。

2.3.3 二维模型计算

不同于一维计算模型，二维模型计算时，需要考虑计算时段间隔的设置，计算时段间隔参考下式进行选取，最终确定的计算时间间隔为15 s，过程线输出间隔为1 h。即

C=(Vb/ΔT)≤1.0

(7)

式中，C为Courant数，最大值为3；Vb为洪水波波速，m/s；ΔT为平均网格大小，m。

2.3.4 计算成果提取

采用二维模型可计算出模型模拟范围内任意断面的河道水位流量关系，二维模型计算基于建模时划分的计算网格，每个网络会充分考虑其下的地形资料。事实上，一个计算网格相当于一个槽蓄水库。

(1)流量过程的提取。模型将给定断面经过的所有计算单元的流量进行平均，求得通过设计断面的总流量过程。

(2)水位过程提取。一维模型进行计算时，认为水面沿河道横断面方向不存在任何变化，即认为某一断面的水面完全水平，二维模型则会充分考虑设计断面沿线的地形变化，计算出的设计断面的水面线沿横断面方向不同计算网络水位不同，可反映真实河道不同位置水面高程不同的情况。因此，需要选取关注网格(如压力水位计所在位置)进行单独网格水位过程的提取。水位流量过程提取后，便可组成设计断面相应的水位流量过程，见图6。

图6 二维计算成果同一断面沿线不同水位分布情况

2.4 成果对比

990号、2200号及2513号设计断面一维和二维水位流量关系分析计算成果对比见图7～9。对比发现，990号断面处一维模型与二维模型水位流量关系计算成果十分接近，分析原因主要是990号断面所处河段局部较为顺直，且无壅水洼地，2200号及2513号断面一维和二维模型计算成果差异较大，主要是因为这两处断面位于河段鱼肚型天然水塘，水流流态复杂，一维断面的直线内插算法无法较好反映真实的洼地地形。此外，二维模型计算出的水位流量关系线呈现出不规则抖动现象，这一现象在2200号及2513号断面十分显著，反映出两断面所在洼地的槽蓄作用，计算成果更能贴近真实情况。

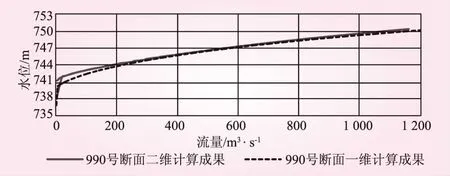
图7 990号断面水位流量关系计算成果对比

图8 2200号断面水位流量关系计算成果对比

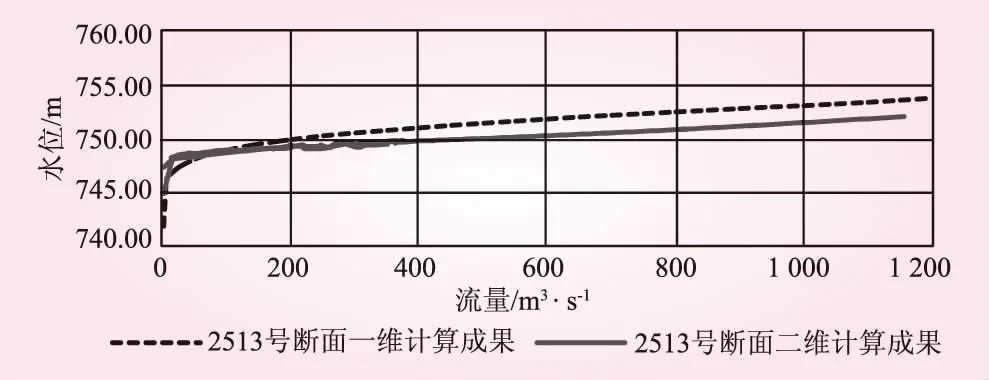
图9 2513号断面水位流量关系计算成果对比

3 结 论

本文以非洲卢阿拉巴河上游河段为例，分别采用一维及二维水力学模型计算并提取了设计断面的水位流量关系，并对一维、二维模型模拟成果进行了对比，对比成果显示：

(1)在河段较为顺直的情况下，模型糙率及下游边界条件选取参数一致时，一维和二维模型的计算成果较为接近；但遇到洼地等水流较为复杂的河段，一维与二维模型的计算成果有一定差异，且差异仍在可接受的范围。

(2)二维水力学模型能够更好地反映计算河段的真实地形。考虑河段每一细微地形变化，模型建立并运行成功后，可根据需要随时提取任意断面的水位流量关系，对于工程前期方案比选十分便利。

(3)二维模型计算的某一断面水位沿断面方向水位存在差异，且断面水位流量关系出现绳套或抖动情况，更能反映真实情况。

综合分析认为，一维水面线计算模型在顺直河段水位流量关系的计算上较为准确；但其对于河段地形复杂的情况，计算时概化可能较为严重，无法反应河段真实地形情况。二维计算模型在水位流量关系的计算时，充分考虑每一处地形差异，计算成果更具参考性。