圆环面S1(R )×S1(r )上的定倾曲线

齐 瑞

(郑州西亚斯学院 教育学院，河南 郑州 451100)

圆环面是三维空间中一类特殊的旋转曲面，在曲面理论研究中占据着重要地位，并且在实际生产生活中有广泛的应用。定倾曲线又被称为螺线，指与固定方向呈恒定角度的曲线，如平面上的阿基米德螺线、圆柱面上的定倾曲线等。关于圆环面和定倾曲线已有大量研究[1-3]，注意到圆柱面是一类旋转曲面，它的定倾曲线与旋转轴呈固定的夹角，而圆环面作为旋转曲面，其方程为

r(θ，φ)=[(R+rcosθ)cosφ，(R+rcosθ)sinφ，rsinθ]。

圆环面可以看成由一个小圆S1(r)绕固定的大圆S1(R)旋转得到的，此时的轴线可以看成是大圆S1(R)。因此，可考虑S1(R)×S1(r)上的定倾曲线。

定义对于圆环面S1(R)×S1(r)上的曲线，如果它在每一点处与中心圆周S1(R)的夹角为常数，则称为该圆环面上的定倾曲线。

本研究通过以下主要定理，建立了圆环面S1(R)×S1(r)上定倾曲线的完全分类。

主要定理圆环面S1(R)×S1(r)上的定倾曲线必为下列3类曲线之一：

①r(θ)=[(R+rcosθ)cosφ0，(R+rcosθ)sinφ0，rsinθ]，其中φ0为常数。

②r(φ)=[(R+rcosθ0)cosφ，(R+rcosθ0)sinφ，rsinθ0]，其中θ0为常数。

③r(φ)=[(R+rcosθ)cosφ，(R+rcosθ)sinφ，rsinθ]，其中φ为θ的函数。

这里的常数φ0=φ(0)，p0=1/φ′(0)由曲线上的点及该点处切向量决定。

上述定理中的曲线①和曲线②分别对应圆环面上的经圆和纬圆。

1 主要定理的证明

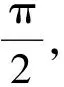
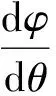
r(φ)=[(R+rcosθ)cosφ，(R+rcosθ)sinφ，rsinθ]，

(1)

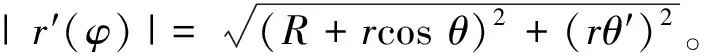
由于r(φ)是定倾曲线，故

即有

(2)

对式(2)两边关于φ求导，得到

注意到θ′≠0，于是有

(R+rcosθ)θ″+rsinθθ′2=0。

(3)

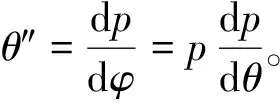
因为p=θ′≠0，所以方程(3)可转化为

(4)

对于初值p(θ=0)=p0，上述方程的解是

(5)

式(5)可化为

注意R>r，利用如下公式[4]:

得到当φ(0)=φ0时，上述方程的解为

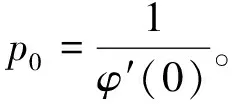
2 结语

本研究的证明方法同样适用于研究管状曲面和一般旋转曲面的定倾曲线。管状曲面的定倾曲线是指与中心曲线成固定角度的曲线，它是圆环面上定倾曲线的一种自然推广。