棉织物含水率对折皱回复角的影响

胡 冰，汪世奎，周雅琼

(合肥师范学院 艺术传媒学院，安徽 合肥 230601)

棉织物具有亲水性好、透气透湿性能优异、柔软亲肤、穿着舒适等优点，但在日常洗涤、穿着和存放过程中，由于折叠和洗涤等外力作用，棉织物会产生急弹性形变、缓弹性形变及塑性形变，从而形成折痕或皱纹，难以恢复到平整状态[1]。折皱回复性能是影响棉织物外观的重要因素，也是考核棉织物性能的重要指标。目前国内外学者对棉织物干态下的折皱回复性能进行了大量研究，主要集中在机械性能或抗皱整理工艺等对棉织物折皱回复性能的影响，以及棉织物本身结构特性如厚度、质量、经纬密度对折皱回复性能的影响等方面，而湿态下棉织物的折皱回复性能在织物洗涤、烘干及护理方面有着重要意义，故有必要对棉织物在不同含水率下的折皱回复性能进行分析和探讨。

1 实验

1.1 试样

选择一种具有代表性的纯棉梭织物作为试样，规格如表1所示。

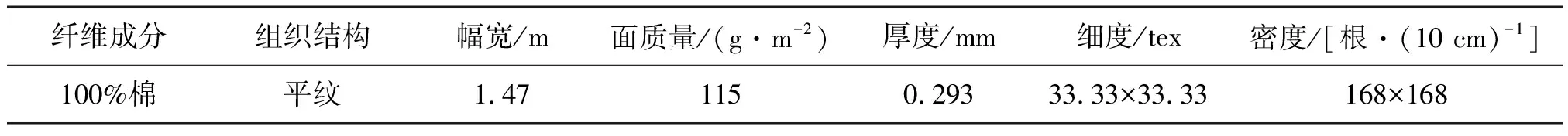
表1 试样规格Tab.1 Sample specification

1.2 控制织物含水率稳定性及均匀性的较优方案

目前没有仪器能控制织物含水率的稳定性及均匀性，考虑织物中水分可自然蒸发，自制一个格状沥水篮，使水分自然沥干且蒸发。此沥水篮由渔线编织，渔线两端绑在塑料篮的镂格上，结合一上一下的编织规律，使渔线均匀受力、相互支撑。渔线编织位置靠近篮口，格网悬空，上、下层空气自然流通，能使织物正反面较为稳定和均匀地含有水分，且易于摆放织物。对于本实验中试样含水率的确定，首先称量未浸湿的试样质量并记录，然后将浸湿试样摆放在上述格状沥水篮中，最后在不同时间点对湿态蒸发的试样称质量，通过公式计算得到含水率。

1.3 实验仪器

选用YG541E型激光织物折皱弹性测试仪来测试织物折皱回复性能，该仪器可测量并计算出试样压重的急弹折皱回复角及缓弹折皱回复角[2]。采用上海天平仪器厂生产的FA110Y型电子天平测量试样质量，精确到±0.001 g。

1.4 实验过程

湿态织物在实验过程中，其试样回复翼易黏附在仪器薄膜上，从而无法得出有效数据。预实验表明，棉织物在含水率超过45%时出现大量无效值，低于45%时无效数据占2.3%，故将折皱回复角实验的含水率临界值定为45%。试样的干质量默认为试样未浸湿状态下的质量，取3次称量的平均值。借鉴织物含水率=[(湿质量-干质量)/湿质量]×100%[2]，对浸湿蒸发后干、湿质量结果进行计算以确定织物含水率。

用YG541E型激光织物折皱弹性测试仪来测量试样在不同含水率下压重的急弹折皱回复角与缓弹折皱回复角，并分别进行记录。各项实验均在温度为(20±2)℃，相对湿度为(65±4)%的环境中进行。将试样裁剪成图1所示的形状。准备50块试样，经向和纬向各25块，压力负荷为10 cN，加压时间为5 min，在称取试样的干质量前将试样水平放置在恒温恒湿实验室内平衡24 h。

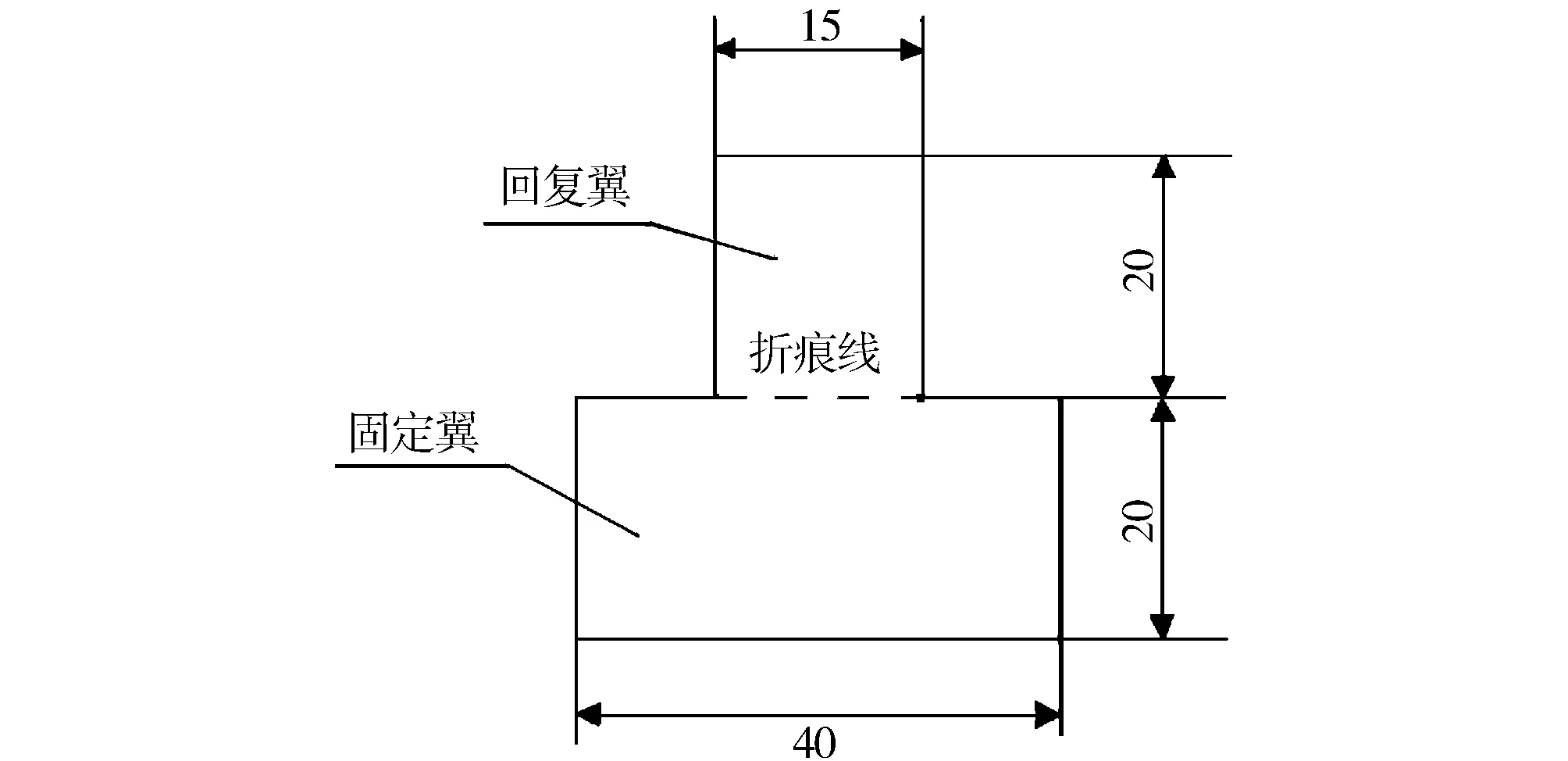
图1 试样尺寸形状(单位：mm)Fig.1 Size and shape of test sample(unit：mm)

2 结果与分析

2.1 实验结果

为方便实验数据的记录及分析，分别用0和1表示试样的经向和纬向，50组试样急弹折皱回复角与缓弹折皱回复角实验结果见表2。

表2 实验结果Tab.2 Experimental results

表2(续)

2.2 相关性分析

对50组试样的含水率、经纬向与急弹折皱回复角、缓弹折皱回复角的相关性进行分析，结果如表3所示。

表3 相关性分析Tab.3 Correlation analysis

由表3可知，含水率与急弹折皱回复角的皮尔逊相关系数为-0.518，与缓弹折皱回复角的皮尔逊相关系数为-0.573，即织物含水率与急弹折皱回复角和缓弹折皱回复角均呈现出显著负相关。由此可知，织物含水率与急弹折皱回复角及缓弹折皱回复角是密切相关的，并且随着织物含水率的提升，其湿态折皱回复性会逐渐变差，织物的抗皱性能也变差。试样经纬向与急弹折皱回复角和缓弹折皱回复角分别呈现低度相关和弱相关关系，皮尔逊相关系数均小于0.3，即试样在湿态条件下，其布纹方向对织物回弹性存在一定影响。这种影响表现为织物的纬向折皱回复角均大于经向折皱回复角，可理解为织物的纬向湿态抗皱性能优于经向湿态抗皱性能。试样为100%纯棉平纹织物，由于平纹组织为一上一下的结构，所以经向和纬向上区别不大，导致经纬向对织物湿态折皱回复性能的影响偏小。

纤维素纤维分子结构一般分为结晶区和无定形区两个区域，结晶区的分子排列整齐，缝隙空洞少，较为稳定，无定形区的分子排列不太整齐，缝隙和空洞较多，密度较低，分子间作用力较小[3-4]。在外力作用下，原始氢键发生断裂，形成新的氢键组合，折皱也由此形成，这也是急弹折皱回复角和缓弹折皱回复角形成的原理。并且，棉纤维中纤维素含量占90%以上，其无定形区达到47%以上[5]，所以棉纤维本身极易起皱。此外，天然纤维无定形区存在大量亲水基团如羟基、羧基等，纤维一旦吸水，水分子以氢键的形式与纤维中亲水基团结合，纤维无定形区分子链变得十分疏松，很容易滑移。棉纤维在水中横截面面积可增大40%以上，而长度仅增加1%～2%。干燥时不均匀回复会导致折皱产生[6-7]，当湿度增加时，纤维材料更具塑性，纤维间的摩擦阻力也会变得更大，这些都会使织物的抗皱性能降低[8]。因此，结合实验结果可知，棉织物在湿态环境下更易起皱，且折皱回复性能随着织物含水率的提升而逐渐降低。

2.3 回归分析

通过上述相关性分析可知，经纬向对试样折皱回复性能的影响较小，下面只研究含水率与折皱回复角的回归关系。从含水率与急弹折皱回复角和缓弹折皱回复角的散点图(图2和图3)可看出，折皱回复角与含水率呈现线性关系。

图2 含水率与急弹折皱回复角的散点图Fig.2 Scatter plot of moisture content andacute-elastic wrinkle recovery angle

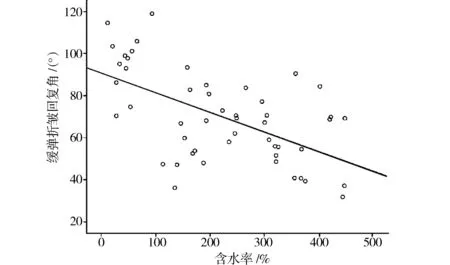
图3 含水率与缓弹折皱回复角的散点图Fig.3 Scatter plot of moisture content andslow-elastic wrinkle recovery angle

一元线性回归研究的是一个自变量对一个因变量的数量关系，除自变量和因变量之间呈现线性关系外，因变量的取值是独立的，故本实验数据可进行自变量为含水率、因变量为折皱回复角的一元线性回归分析。

(1)急弹折皱回复角

织物含水率与其急弹折皱回复角之间有一定的相关关系，具体见表4和表5。由表4和表5可知，尽管R2=0.269，但F=17.622，大于3，显著性值为0.000，小于0.05，表示该模型的建立是有意义的。

表4 含水率对急弹折皱回复角的回归模型分析Tab.4 Regression model analysis of moisture content on acute-elastic wrinkle recovery angle

表5 含水率对急弹折皱回复角的回归模型方差分析Tab.5 Variance analysis of regression model of moisture content on acute-elastic wrinkle recovery angle

该回归模型的常数项为71.801，t值为14.445，显著性值为0.000，含水率的未标准化系数为-81.090(表6)，故织物含水率与急弹折皱回复角的线性回归方程为y=71.801-81.090x。式中：y为急弹折皱回复角，x为织物含水率。

表6 含水率与急弹折皱回复角的模型系数Tab.6 Model coefficients of moisture content and acute-elastic wrinkle recovery angle

(2)缓弹折皱回复角

织物含水率与其缓弹折皱回复角之间也有一定的相关关系，具体见表7和表8。由表7和表8可知，尽管R2=0.329，但F=23.500，大于3，显著性值为0.000，小于0.05，表示该模型的建立同样是有意义的。

表7 含水率对缓弹折皱回复角的回归模型分析Tab.7 Regression model analysis of moisture content on slow-elastic wrinkle recovery angle

表8 含水率对缓弹折皱回复角的回归模型方差分析Tab.8 Variance analysis of regression model of moisture content on slow-elastic wrinkle recovery angle

该回归模型的常数项为90.691，显著性值为0.000，含水率的未标准化系数为-92.873(表9)，故织物含水率与急弹折皱回复角的线性回归方程为y=90.691-92.873x。式中：y为缓弹折皱回复角，x为织物含水率。

表9 含水率与缓弹折皱回复角的模型系数Tab.9 Model coefficients of moisture content and slow-elastic wrinkle recovery angle

(3) 验证实验

为了对模型准确率进行验证，选取与上述实验规格相同的5块试样，根据蒸发时间将含水率大致控制在均匀档差范围内，计算得到准确值分别为5.9%、11.3%、20.6%、33.2%、42.1%，并将试样分别编为1#、2#、3#、4#、5#，测试试样的急弹和缓弹折皱回复角，结果如表10所示。

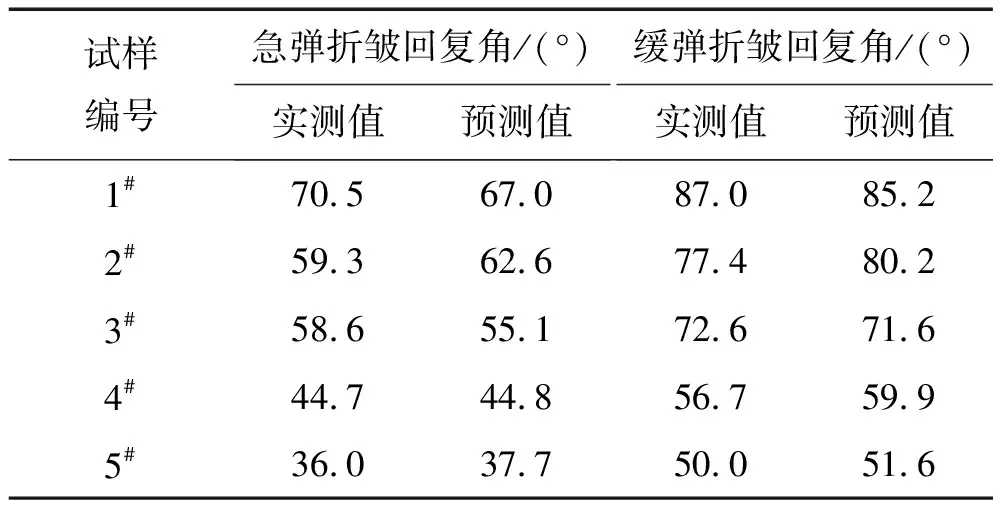
表10 验证实验结果Tab.10 Results of verification experiment

表10中的实测值和预测值均符合正态分布，再进行配对样本t检验分析，结果如表11和表12所示。在急弹折皱回复角实测值与预测值的配对样本t检验中显著性值为0.795，在缓弹折皱回复角实测值与预测值最大差值的配对样本t检验中显著性值为0.394，均大于0.05，即急弹折皱回复角和缓弹折皱回复角的预测值与实测值没有显著性差异。这说明本实验构建的回归方程是有意义的，并能够较好地应用于纯棉织物湿态下的折皱回复角分析。

表11 急弹折皱回复角实测值与预测值的配对样本t检验Tab.11 Paired-samples t test of measured and predicted values of acute-elastic wrinkle recovery angle

表12 缓弹折皱回复角实测值与预测值的配对样本t检验Tab.12 Paired-samples t test of measured and predicted values of slow-elastic wrinkle recovery angle

3 结论

本研究通过线性相关性分析得到织物含水率和折皱回复角的线性负相关关系，急弹折皱回复角和缓弹折皱回复角均随含水率增大而变小，试样干态和湿态下的折皱回复性能有较大差别，干态下试样的折皱回复性能明显优于湿态下。并且，利用线性回归分析建立了织物含水率与急弹折皱回复角和缓弹折皱回复角间的回归模型，验证了该模型的准确性。