轴向运动梁稳定性分析的通用有限元模型及应用
2022-06-21随岁寒
李 岩,随岁寒
(1.商丘工学院 教育与现代艺术学院,河南 商丘476000; 2.商丘工学院 机械工程学院,河南 商丘476000)
在机械工程中传动带、带锯和缆索等皆可模型化为轴向运动梁,受到电机振动的影响,这些轴向运动构件在工作中也不可避免地发生振动。轴向运动速度与这些装备的工作效率息息相关,且轴向速度对振动又有重要影响,过快的轴向速度会导致振动失稳而对装备造成破坏,因而有必要对轴向运动系统振动特性展开研究。近年来,轴向运动梁振动及其稳定性的研究成果被大量报道。刘金建等[1]采用多尺度法和微分求积法研究了轴向运动黏弹性Euler梁自由振动的稳定性。王波等[2]利用微分求积法研究轴向运动黏弹性Rayleigh梁的非线性受迫振动。林鹏程等[3]基于Timoshenko梁理论研究了3种不同边界条件下轴向运动功能梯度材料梁在热冲击载荷作用下的自由振动响应。周远等[4]研究了黏弹性阻尼作用下轴向运动Timoshenko梁的振动特性。Lee等[5]在经典梁理论的基础上建立了传递矩阵方法,研究轴向拉伸载荷和移动速度对3种不同端部条件下轴向移动梁固有频率的影响。Wang等[6]基于非局部应变梯度理论,考虑两种尺度效应,利用Galerkin方法研究了轴向运动纳米梁的分叉和混沌。Liu等[7]对轴向加速黏弹性Timoshenko梁的参数稳定性进行了分析和数值研究。Hao等[8]结合Timoshenko梁理论研究了带有形状记忆合金层合梁的轴向运动非线性动力特性。Sarparast等[9]采用非局部应变梯度Rayleigh梁模型,研究了黏弹性基础上轴向小尺度运动梁在湿热环境下的振动行为和动力稳定性。刘慧贤等[10]基于Euler梁模型研究了中间支撑条件下轴向运动微梁的自由振动问题。
需要指出的是,现有文献多是研究基于Euler-Bernoulli梁模型[1,5,10-11]和Rayleigh梁模型[2,9,12-13]的细梁,也有部分文献研究了基于Timoshenko梁模型的粗梁[3,4,7-8],但利用三阶剪切梁模型研究轴向运动梁振动及其稳定性的文献鲜有报道。相对于Timoshenko梁模型,三阶剪切梁模型不需要剪力修正系数,且无论细梁还是粗梁在三阶剪切模型下都能获得很好的求解精度。由于轴向运动梁系统中科氏加速度的存在,使得特征值难以解析求解,故诸多数值方法被用于求解该类问题,如微分求积法[2]、传递矩阵法[5]、Galerkin法[6]等。有限元法作为一种应用广泛的数值方法,拥有标准化的操作流程,推导系统有限元方程的过程中不需要导出系统控制方程,故利用有限元法分析轴向运动系统特性具备一定优势。目前,利用有限元法研究轴向运动梁的文献多集中在轴向运动悬臂梁方面[12-14]。在实际应用中,轴向运动结构往往在两端受到支承,本研究正是针对这一应用形式开发了对应的有限元动力学模型。目前在商业计算软件(如ANSYS、ABAQUS等)中尚无针对轴向运动梁类问题的专用模块,本研究建立的通用有限元模型可同时适用于细梁和粗梁,是一种简便的建模方法。
Stylianou等[12]首创利用Lagrangian方程得到轴向运动悬臂梁有限元动力学方程,后来用有限元法研究轴向运动悬臂梁的文献也多采用这一方法[13]。国内也有学者利用Lagrangian方程得到两端支承轴向运动梁的有限元方程[14],但该研究仅限于细梁。Hamilton原理[15]和虚功原理[16]常被用来建立动力学系统的有限元方程,且虚功原理便于明确速度相关项的物理意义,进而深入揭示轴向运动梁动力学特性的成因。本研究从虚功原理出发,考虑三阶剪切理论下的位移场并结合几何方程和物理方程,经推导得到了轴向运动梁系统的有限元方程,并探讨了轴向运动速度的衍生项即离心力和科氏力对系统动力学规律的贡献。
1 动力学模型
为得到轴向运动梁系统有限元方程,利用虚功原理表达式
δU=δW+δF,
(1)
式中:δU、δW和δF分别为系统势能变分、惯性力虚功、科氏力与离心力虚功。
采用一种2节点梁单元,沿梁长度方向将梁划分为若干个单元,单元横向位移和截面转角利用形函数表达[17]如下:
(2)
(3)
式中:N1和N2是拉格朗日形函数;H1~H4是Hermite形函数。
首先,利用Reddy三阶梁理论的位移场[18]
(4)
w(x,z)=w(x),
(5)
式中:α=4/3h2。利用式(4)、(5)并结合式(2)、(3),得惯性力虚功
(6)
为得到应变能变分,利用如下几何方程:
(7)
(8)
然后,利用式(2)、(3),将几何方程整理成矩阵形式
(9)
式(9)可简化为
ε=[B]{d},
(10)
及物理方程
(11)
将方程(11)简化为
σ=[D]ε。
(12)
利用式(10)、(12),可得应变能变分
(13)
最后,给出科氏力和离心力虚功[19-20]:
(14)
将式(6)、(13)、(14)代入虚功原理表达式(1),得到轴向运动梁系统有限元平衡方程
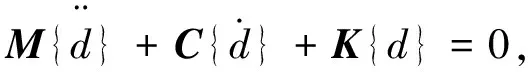
(15)

2 数值验证
将方程(15)结合两端固支的边界条件,可求解得到轴向运动梁系统的各阶固有频率。这一频率通常为复数,虚部代表固有频率的数值,实部用于表征系统稳定性,实部为0或者为负值代表系统稳定,实部为正值代表系统失稳。所需材料的物理参数如表1所示。

表1 物理参数Tab.1 Physical parameters
为验证本研究建立的有限元模型的可靠性,在轴向速度为0的条件下,分别给出3种典型细长比对应的系统前三阶固有频率,并将其与ANSYS软件所得结果进行了对比(表2至表4)。由表2至表4可知,从细梁到粗梁的变化过程中,前三阶固有频率的最大误差不超过1.7%,证明所建立的有限元模型有效。
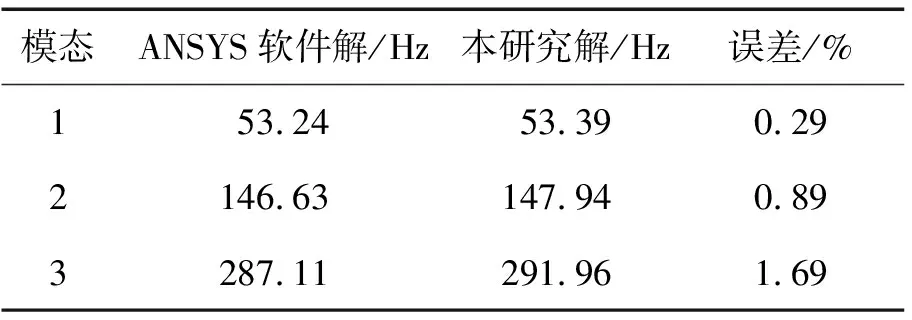
表2 本研究解与ANSYS软件解对比(h/L=0.01)Tab.2 Solution of this study and comparison with ANSYS (h/L=0.01)
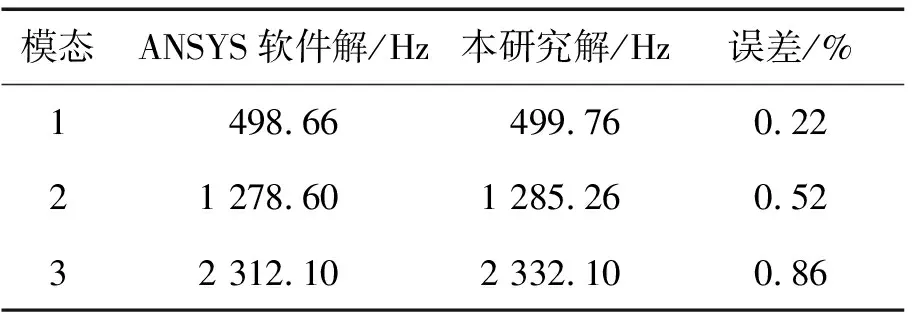
表3 本研究解与ANSYS软件解对比(h/L=0.1)Tab.3 Solution of this study and comparison with ANSYS (h/L=0.1)
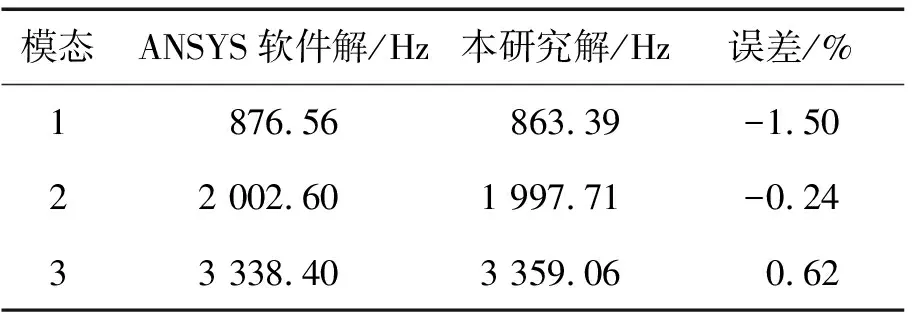
表4 本研究解与ANSYS软件解对比(h/L=0.2)Tab.4 Solution of this study and comparison with ANSYS (h/L=0.2)
图1至图3分别给出了3种典型细长比条件下,系统前三阶复固有频率随轴向速度的变化趋势。对比3组图可见,固有频率实部和虚部的变化规律类似,所不同的是特定位置的具体数值。以图1为例,当轴向速度增至94 m/s时,固有频率虚部降低到0,这一速度为临界速度。达到临界速度后,若继续增加速度,则固有频率的实部开始出现正值,即系统失稳,第一阶失稳速度为94~136 m/s。算例显示,在轴向速度大于临界速度后,速度的任何微小波动都会造成系统固有频率的实部在正值和负值之间跳跃。如图1显示,每个椭圆形包含的速度范围都是一个失稳速度区域,速度继续增加,超过了这一椭圆包含区后,系统又表现出稳定性,即两个椭圆之间的间隙区域所对应的速度范围系统处于稳定状态,这一稳定速度为137~147 m/s。第二个椭圆包含的速度区域代表第二阶固有频率的失稳区域,第二阶失稳速度为148~186 m/s,与第一阶频率的第二次失稳速度范围重合。后续经历较短暂的稳定区域后,紧接着出现第一阶固有频率的第三次失稳区域。对比图1的实部和虚部可以发现,第二阶和第三阶固有振动失稳时,相应阶次固有频率的虚部并不降低到0。同理,第三阶固有频率也有相应的失稳区域。
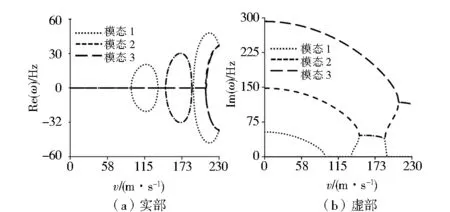
图1 轴向运动梁固有频率实部和虚部与速度的关系(h/L=0.01)Fig.1 The relationship between natural frequencies and axial velocity (h/L=0.01)
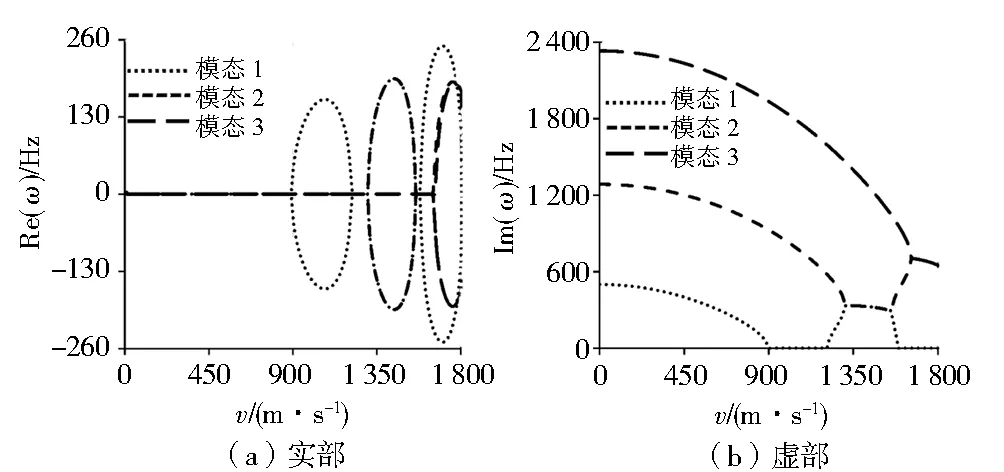
图2 轴向运动梁固有频率实部和虚部与速度的关系(h/L=0.1)Fig.2 The relationship between natural frequencies and axial velocity(h/L=0.1)
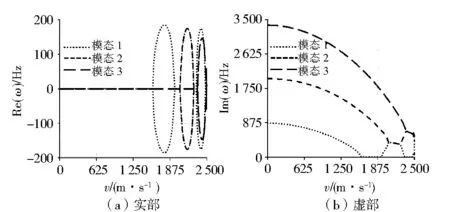
图3 轴向运动梁固有频率实部和虚部与速度的关系(h/L=0.2)Fig.3 The relationship between natural frequencies and axial velocity (h/L=0.2)
为探究速度增加则各阶固有频率降低的根源,考察方程(15)可以发现,相对于无轴向运动结构,这一方程增加了离心力项和科氏力项,可以据此判定系统固有频率降低是因为受到离心力和科氏力的共同作用。为深入揭示这两项在多大程度上影响固有频率,图4至图6分别给出了3种典型细长比条件下,系统第一阶复固有频率(虚部)与轴向速度的对应关系,并给出了仅考虑离心力和仅考虑科氏力这两种条件下的对比数据。可见,低速运动时3条线比较接近,因为此时离心力和科氏力都不大。当速度较高时,仅考虑离心力的情形更接近实际,也就是说高速运动时离心力起主导作用。科氏力是轴向速度和梁中面转动角速度的乘积,由于离心力的主导作用,速度较高时梁中面转动角速度较低,此时科氏力进一步被削弱。
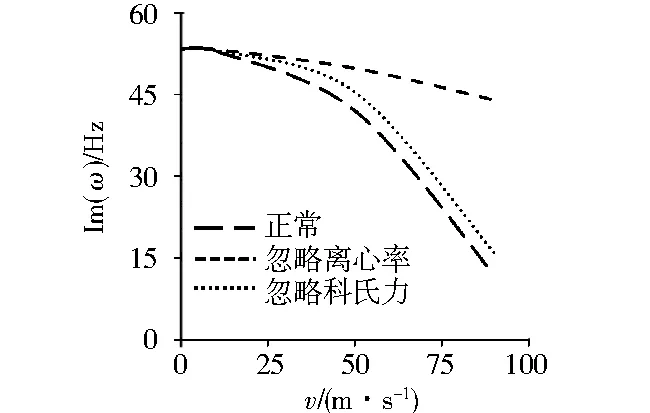
图4 离心力和科氏力对第一阶固有频率的影响(h/L=0.01)Fig.4 The impact of centrifugal force and Coriolis force on first natural frequencies(h/L=0.01)
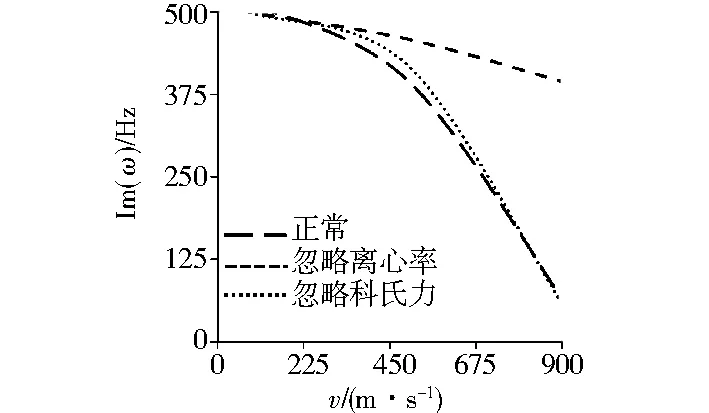
图5 离心力和科氏力对第一阶固有频率的影响(h/L=0.1)Fig.5 The impact of centrifugal force and Coriolis force on first natural frequencies(h/L=0.1)
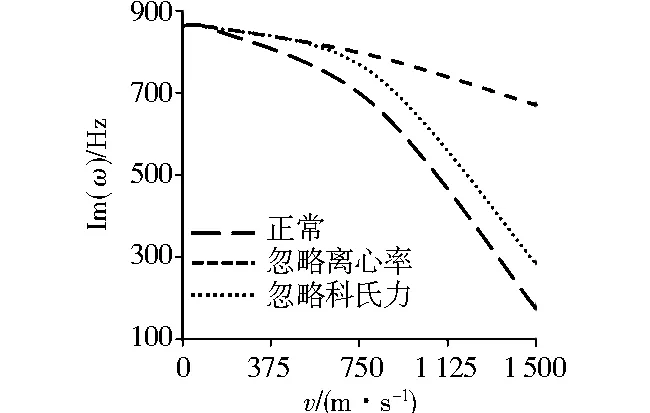
图6 离心力和科氏力对第一阶固有频率的影响(h/L=0.2)Fig.6 The impact of centrifugal force and Coriolis force on first natural frequencies(h/L=0.2)
3 结论
本研究针对轴向运动梁,基于三阶剪切理论和虚功原理建立了一个对细梁和粗梁通用的有限元动力学模型,给出了3种典型细长比条件下的系统前三阶复固有频率,并通过与ANSYS软件的计算结果对比,证实了本模型的准确性。具体结论如下:
(1) 所建立的有限元模型对细梁和粗梁都有较高的计算精度。
(2) 第一阶固有频率进入失稳区域的标志是固有频率的虚部降至0。
(3) 各阶固有频率都有特定的失稳区域,相邻两阶失稳区域之间会有一段稳定区域。
(4) 速度增加而各阶固有频率降低的原因是系统离心力和科氏力的共同作用,且离心力起主导作用。
