同时起爆单排炮孔等效均布荷载的计算方法*

孙金山，张鸿昱，闫国华,贾永胜,赵国堂，姚颖康,谢全民

(1.江汉大学 a.精细爆破国家重点实验室;b.爆破工程湖北省重点实验室，武汉 430023；2.中国国家铁路集团有限公司，北京 100844)

数值模拟是开展工程爆破理论与技术研究的重要手段，当对大规模炮孔产生的荷载或爆破振动进行数值模拟时，爆炸荷载的施加是其重点和难点。目前，爆破荷载的模拟和施加主要有三种技术途径：一是建立炮孔及炸药单元，利用炸药材料的爆轰产物状态方程来模拟爆炸荷载，并直接施加在炮孔壁上；二是直接在孔壁上施加一个随时间变化的均布压力；三是不考虑炮孔的形状，仅在炮孔中心连线(面)上施加等效均布荷载。

第一种技术途径中的爆轰产物状态方程是计算爆轰产物压力、体积、温度等物理量之间的数学方程，国内外学者曾提出了BKW[1]、JCZ[2]、VLW[3]、Davis[4]、JWL等多种模型[5]。其中，JWL状态方程在爆炸数值模拟中应用广泛[6-8]，然而，该方程中大量的未知参数需要通过圆筒试验及流体动力学计算来确定，且其忽略了岩石破碎及气体逸出过程的影响。因此，在实际计算过程中，人们多采用互相参考的方式来近似确定其计算参数，其输出结果的可靠性与实际荷载间的差异性往往难以考证。同时，采用该数值模拟方案时需要建立非常精细的炮孔及炸药单元，需要花费大量的建模及计算时间。

第二种技术途径直接在孔壁上施加均布压力，不需要设置复杂的炸药材料参数，且可适用于更多的具有动力计算模块的数值模拟软件。目前，常用的孔壁爆炸压力计算模型是双折线模型和双指数模型。其中，双折线三角形分段函数荷载模型简单实用[9]，其仅有升压时间、卸压时间和峰值压力三个参数，而峰值压力可通过C-J爆轰模型计算，时间参数则可通过经验公式估算得到。该荷载模型未考虑炸药爆炸特征，也未考虑炮孔的孔深、孔径和堵塞等对爆炸荷载的影响，因此，其峰后荷载的时间历程计算误差较大。双指数函数由Starfield提出[10]，该模型为连续光滑函数，更便于理论分析和数值模拟。Jong对该模型进行了改进[11]，提出了其关键参数的计算公式，并使荷载时程曲线更接近实验结果。但该模型中关键参数M和N的取值同样未考虑爆破破岩过程的特征，因此其适用范围受到限制。另外，第二种技术途径也需要建立精细的炮孔网格，建模和计算过程也较复杂和耗时[12-14]。

鉴于数值模拟中炮孔几何离散(网格划分)和计算过于复杂的问题，少量学者对如何将炮孔载荷等效成为均布载荷进行了研究。如许红涛提出了一种在炮孔中心连线上施加等效均布荷载的方法[15]。张玉成提出了将炮孔壁上荷载等效成为面荷载的方法[16]。李启月提出了微差爆破荷载的等效施加方法[17]。杨建华根据炮孔周围岩石破坏情况的空间分布特征等[18]，提出可在炮孔等效弹性界面上施加爆破荷载。赵婉婷对比计算后认为[19]，在数值模拟中分析炮孔远区岩石的动态响应时，将荷载直接等效施加在开挖轮廓面上代替施加在炮孔周边弹性边界上的处理方式是可行的。罗笙提出将爆破载荷等效为法向冲击载荷可以有效模拟爆破开挖下对岩体的损伤效应[20]。因此，采用等效均布爆破荷载虽不能模拟炮孔周围介质的力学响应，但在模拟炮孔远区的振动和结构响应等问题时，其误差是可以接受的。然而，上述研究多是对许红涛提出方法的改进和数值模拟验证，在实际工程应用时这些研究中的峰值爆炸荷载及均布荷载等效方式等仍需进一步研究。

因此，鉴于工程爆破理论与技术研究中经常涉及的爆破荷载施加问题，本文针对将炮孔载荷等效为均布载荷的方式方法进行了理论探讨，对既有的等效方法进行了讨论并提出了新的等效方法。

1 许红涛提出的等效均布荷载计算方法及其讨论

为避免进行炮孔的细节建模和几何离散，许红涛提出将同排起爆的炮孔圆心连成一条线(二维空间)，或将其轴线连成一个平面(三维空间)，再在该线或面上施加均匀的动荷载。如图1所示，假定单个炮孔壁上作用有压力P(t)，炮孔直径为db，孔间距为ab，根据文献[9]可以将如图1(a)所示作用在炮孔壁上的压力等效为如图1(b)所示的等效均布压力，其等效公式为

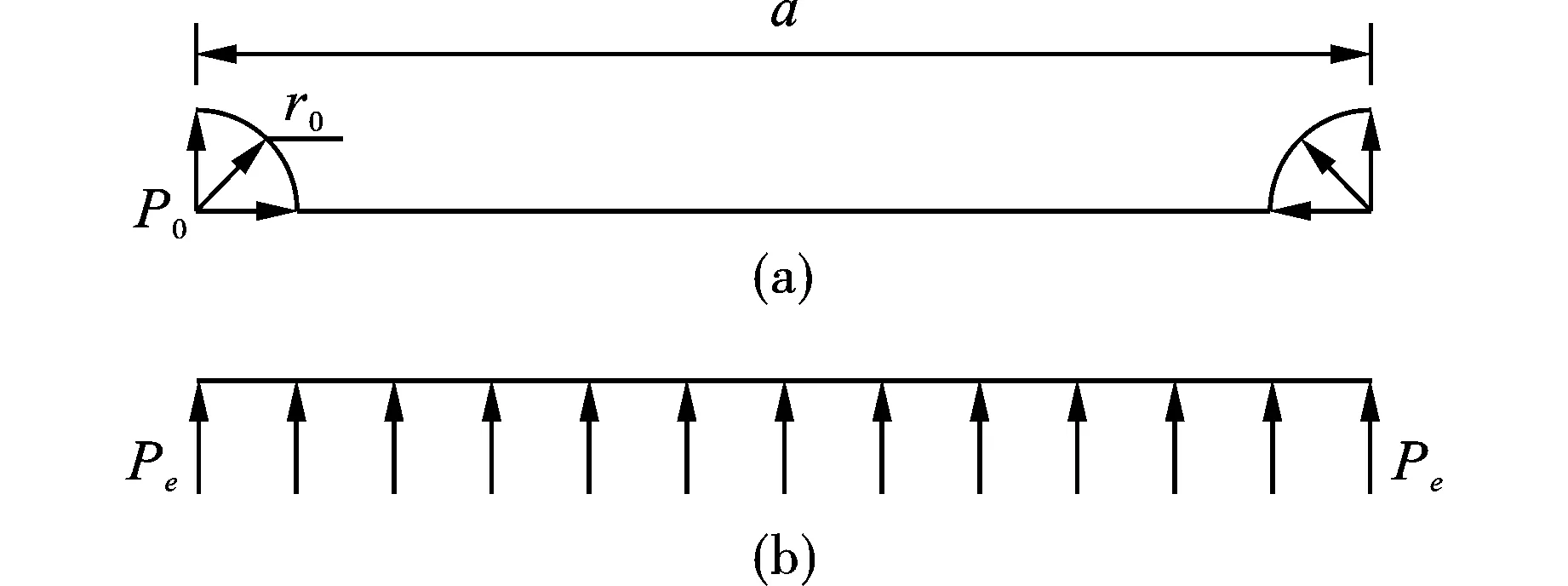
图 1 爆破荷载等效施加示意图[15]

(1)

许红涛在文献[15]采用三角形荷载时程曲线构建均布荷载函数，并建议炮孔孔壁爆炸荷载峰值计算方法分为耦合装药和不耦合装药两种情况。耦合装药条件下，炮孔壁上的压力可以视作炸药的轰爆压力，由下式进行计算[9]

(2)

式中:ρe为炸药密度；D为炸药爆炸速度；γ为炸药爆轰的等熵指数取值一般为3.0。

装药不耦合系数较小时，炮孔峰值压力为[9]

(3)

式中，dc为装药直径。

装药不耦合系数较大时，炮孔峰值压力为[9]

(4)

式中：ν为爆生气体的等熵指数，一般取值1.4；pk为炸药的临界压力。

文献[15]给出的爆破荷载等效方法，简便易行，适用于炮孔远区的一些问题的分析，但其存在两个问题：

(1)文献[15]中虽然简要说明了式(1)～(4)是根据圣维南原理推测而来的，但未给出严格的理论推导，也未阐述将炮孔径向压力转化为炮孔连线的法向荷载的过程。

(2)不耦合装药条件下，炮孔孔壁峰值压力的计算方法忽视了压力增大系数的影响，这导致其孔壁压力计算值偏小。

因此，上述等效均布爆破荷载计算方法的可靠性是值得商榷的。

2 同时起爆单排炮孔均布荷载等效计算的新方法

为对许红涛提出的单排炮孔均布荷载等效计算问题进行理论推导，对两个相邻炮孔的荷载叠加问题进行了平面应变条件下的分析。如图2所示，单排炮孔同时起爆时，在距离炮孔中心连线的y=0.5ab处，相邻炮孔的叠加作用十分显著，此时界面上的应力主要为压应力作用。炸药爆炸产生的应力波在岩体中传播时，其峰值与距离的增加成反比[21]，设炮孔内孔壁上的径向压力为P(t)，则在x=ax，y=0.5ab的界面上，炮孔径向压力传播至指定距离并进行平面分解后，在y方向产生的应力为

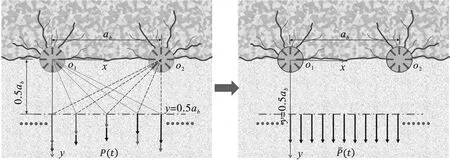
图 2 均布荷载等效图

(5)

将O1孔在x=0～0.5ab，y=0.5ab区域的上的应力式(5)进行积分得到该区域上的合力，并在x=0～0.5ab上对该合力进行平均，即将合力平均分配在0.5ab长度上，得O1孔在该区域产生的等效均布荷载为

(6)

根据上述荷载等效方法，将O2孔在x=0～0.5ab，y=0.5ab区域的应力根据式(5)进行积分计算合力，并对该合力平均，得等效均布荷载为

(7)

在x=0.5ab～ab，y=0.5ab区域，由于两炮孔的对称性等效荷载计算式(6)、(7)同样适用，因此，O1和O2两炮孔在x=0～ab，y=0.5ab边界上，产生的y方向的叠加荷载等效平均值为

(8)

忽略其他更远炮孔的孔壁压力在x=0～ab，y=0.5ab区域的叠加，可近似认为式(8)即为单排炮孔产生的垂直于其炮孔连线方向的等效均布荷载。显然，式(8)与许红涛提出的式(1)明显不同。

如文献[18]和[19]所述，考虑炮孔壁周围岩石的破坏将导致应力波的非线性衰减，还可考虑将荷载施加在炮孔外的临界弹性边界上，此时，爆炸荷载变为弹塑性交界面上的应力Pe(t)，而荷载施加在弹塑性界面r=de处，则均布荷载为

(9)

式中，Pe(t)和de则需根据岩石强度进行计算，因此(9)式的应用不如(8)式方便，但更适用于距离炮孔更近处的工况的分析。

其次，由于许红涛计算炮孔压力峰值时忽略了孔壁处压力增大倍数n(因动压作用产生)，因此实际应采用更可靠的炮孔壁峰值压力计算公式。

目前，计算任意不耦合系数下炮孔壁压力峰值的方法主要有等熵膨胀法和爆轰产物最大扩散速度法。其中，等熵膨胀法应用较为广泛。小不耦合系数装药爆破过程中，爆生气体的膨胀只经历等熵膨胀过程，炮孔孔壁压力峰值计算公式为[22,23]

(10)

式中，n为爆轰产物碰撞炮孔壁时的压力增大系数，耦合装药时可取n=1，根据参考文献[21]不耦合装药时一般取n=10，其它符号同上。

3 数值模拟验证

为验证本文推导的荷载等效方法的可靠性，采用动力有限元软件建立三个长方体数值模型。各模型的横截面尺寸均为900 mm×900 mm，高4000 mm，如图3所示。

图 3 数值模型Y方向应力云图(单位：Pa)

模型(a)下部均匀布置3个半炮孔，直径0.04 m，炮孔中心间距0.235 m，在孔壁上施加均布法向荷载。模型b、c底部为平面，分别施加许红涛和本文计算得到的法向等效均布荷载，模型顶部均施加固定约束。

模型采用线弹性材料，密度为2500 kg/m3，弹性模量E=30 GPa，泊松比μ=0.2，不考虑其阻尼系数。炮孔内炸药直径dc=0.032 m，密度ρe=1200 kg/m3，爆轰速度D=3300 m/s，爆轰产物碰撞炮孔壁时的压力增大系数n=10。孔壁以及均布荷载均采用三角形荷载时程曲线，升压作用时间0.1 ms，卸压作用时间0.7 ms。

根据许红涛和本文的方法，分别计算孔壁径向荷载和等效加载面上的均布荷载峰值，如表1所示。分别在数值模型(a)上施加孔壁均布荷载，在模型(b)上峰值为0.729 GPa和0.111 GPa的等效均布荷载。

表 1 炮孔壁荷载峰值和等效均布荷载峰值

计算结果显示，模型(a)中随着监测点与炮孔距离的增大，模型竖直方向(y方向)的峰值应力逐渐减小至约120 MPa，而模型(b)和模型(c)则分别为108 MPa和725 MPa。因此，计算结果表明，孔壁压力一致的条件下，距离炮孔中心连线约1.5 m处，公式(9)计算得到的等效均布荷载与炮孔数值模型计算结果基本一致，且低10%左右，其原因可能是忽略了其它炮孔在该处的叠加效应；而许红涛提出的模型约为炮孔数值模型计算结果的6倍，显然误差是不可接受的。

表 2 模型各单元应力峰值(单位：MPa)

4 结论

鉴于钻孔爆破数值模拟过程中经常遇到的爆破荷载施加问题，对3种常用的方法进行了讨论，并对许红涛提出的实用性较好的等效均布荷载计算方法进行了讨论，并提出了新的等效计算模型，得到的主要结论如下。

(1)许红涛提出的等效均布荷载计算方法中，等效计算公式以及炮孔壁峰值压力均存在明显的错误，而两个误差相叠加后，导致其最终计算结果与精确值接近。

(2)在笛卡尔坐标系下，通过对炮孔壁径向荷载进行分解与合成，得到了在炮孔远区的炮孔连线法向均布应力的计算公式，以及作用在炮孔外弹塑性界面荷载的等效均布荷载计算公式。

(3)因为工程爆破中往往采用径向不耦合装药，因此炮孔壁峰值压力应考虑爆轰产物碰撞炮孔壁时的压力增大系数。

(4)通过动力学数值模拟，对比了本文提出模型与许红涛计算模型的准确性。结果显示：根据许红涛模型得到的均布应力是数值模型准确解的6倍左右，而根据本文计算模型得到的均布应力与准确解基本吻合，且比准确解低10%左右。

(5)本文模型计算结果比准确值偏小的原因是，仅考虑了两个相邻炮孔在其中间区域处应力的叠加，忽略了两炮孔以外的其它炮孔的应力贡献。