采石场开采爆破炮孔的布置优化❋

2022-01-11门金龙陈邑星郑鸿区蔡冲冲熊碧波

爆破器材 2022年1期

门金龙陈邑星郑鸿区蔡冲冲熊碧波

①广东石油化工学院（广东茂名，525000）②中国核工业二三建设有限公司（北京，101300）

引言

岩石爆破是国内外常用的矿产资源开采手段。但爆破开采存在成本较高、爆破效率较低、安全隐患较大等问题。因此，降低爆破成本、提高爆破质量以及加强爆破作业安全系数一直是矿产爆破开采的主要研究方向[1]。相关研究始于20世纪70年代。Kutter等[2]对岩石的爆破过程进行研究，并提出爆炸气体压力场和爆炸应力波致使岩石碎裂的理论。Yang等[3]利用试验研究爆破应力波的叠加与干涉对岩石裂纹的影响，对采矿的裂纹研究提供了依据。Yi等[4]研究了相邻爆破炮孔对应力波传播的影响，结果表明，两相邻炮孔延长线上的拉应力由于应力波叠加而减小。高士才等[5]通过水泥沙浆台阶爆破试验，提出一种能够增强爆炸气体催生爆炸孔周围裂隙的方案。陈浩哲[6]采用有限元仿真研究不同起爆时差对爆破效果的影响规律，提高了光面爆破的爆破效果。李洪伟等[7]采用数值模拟研究岩石爆炸裂纹发现，炮孔周围裂纹与粉碎数量随炮孔间距离的增加而增多。然而，国内外对矿山岩石的爆破理论研究大多基于地下开采的爆破机理、炮孔布置和爆破作业安全等问题，对露天开采的多炮孔爆破布置的研究相对较少。

结合广东省茂名市某露天采石场爆破作业的实际问题，采用数值模拟与理论计算相结合的方法，分析采石场爆破机理，优化炮孔排布方式，为提高采石场爆破开采效率提供技术支持。

1 岩石爆破理论

岩石爆破的破碎效应影响着工程项目的实际进程和效益，同时也关系到矿山、公路等基础工程的地质稳定性[8]。研究并揭示岩石爆破的破碎机理对促进爆破理论及相关技术的发展、提高实际工程效益具有重大的实际意义[9]。

1.1 有限元理论

式中:M为总质量矩阵；̇x(t)为总节点的加速度矢量；P为总载荷矢量；F为单元应力场的等效节点力矢量。

1.2 岩石爆破过程理论计算

岩石中发生爆炸时，形成一团高温、高压气体，在高压气体和空气介质的界面处，爆炸产物以极高的速度向周围扩散，压缩周围的空气，像活塞一样把能量传给压缩的空气层，使其压力、密度等急剧升高，产生一系列的压缩波，最终叠加形成冲击波。冲击波作用于岩石体，产生远大于岩石抗压强度的径向和切向压应力[11]，使岩壁受到强烈压缩而形成一个空腔，并不断扩大，从而形成岩石的压碎区[12]。研究爆炸径向应力优化开采炮孔布置时，忽略爆炸法向应力的影响，岩石爆破过程理论计算[13]的参考公式如下。

1.3 开采炮孔有限元模型的建立及参数设置

某露天采石场位于广东省茂名市南部，占地面积为0.082 km2，设计生产规模为3×105m3/a，探明资源储量为3×106m3，主要开采建筑用花岗岩。

1.3.1 有限元模型的建立

运用有限元处理软件Hypermesh建立10 m×10 m×10 m的数值模型。单炮孔爆破模拟和双炮孔爆破模拟分别采用1/4、1/2模型，对称面上施加对称约束。数值模型采用非反射边界以模拟无限远的冲击波传播过程，如图1～图2所示。

图1 有限元模型Fig.1 Finite element model

图2 炮孔分布模型Fig.2 Distribution model of blast holes

为避免在炸药爆炸瞬间应力的急剧衰减，模型中对炮孔周边区域的六面体网格进行细化，如图3。

图3 炮孔周边网格局部细化Fig.3 Local refinement of the mesh around the blast hole

1.3.2 材料参数

选用2＃乳化炸药，材料参数见表1。

表1 2＃乳化炸药材料参数Tab.1 Material parameters of 2＃emulsion explosive

选取3＃岩石材料，主要力学参数见表2。

表2 3＃岩石材料参数Tab.2 Material parameters of 3＃rock

在采石场爆破数值模拟中，炮孔孔径设为0.15 m，爆破高度为3 m。起爆点为药柱上平面中心位置。爆破后，分析各孔径排布方式的爆炸效果，并根据爆破效果选出最优布孔方式。

2 采石场单孔爆破开采

结合露天采石场的现场情况，建立数值模型模拟现场单孔爆破。由图4可知，单孔爆破的岩石最上层应力云图整体呈圆环状，应力随着扩散半径的增加而减小。在距单孔爆破中心R=1.48 m的爆破范围内，单元应力全部达到岩石材料的抗压强度，即岩石发生破碎。因此，在2＃乳化炸药单孔爆破作业时，有效爆破半径为1.48 m。

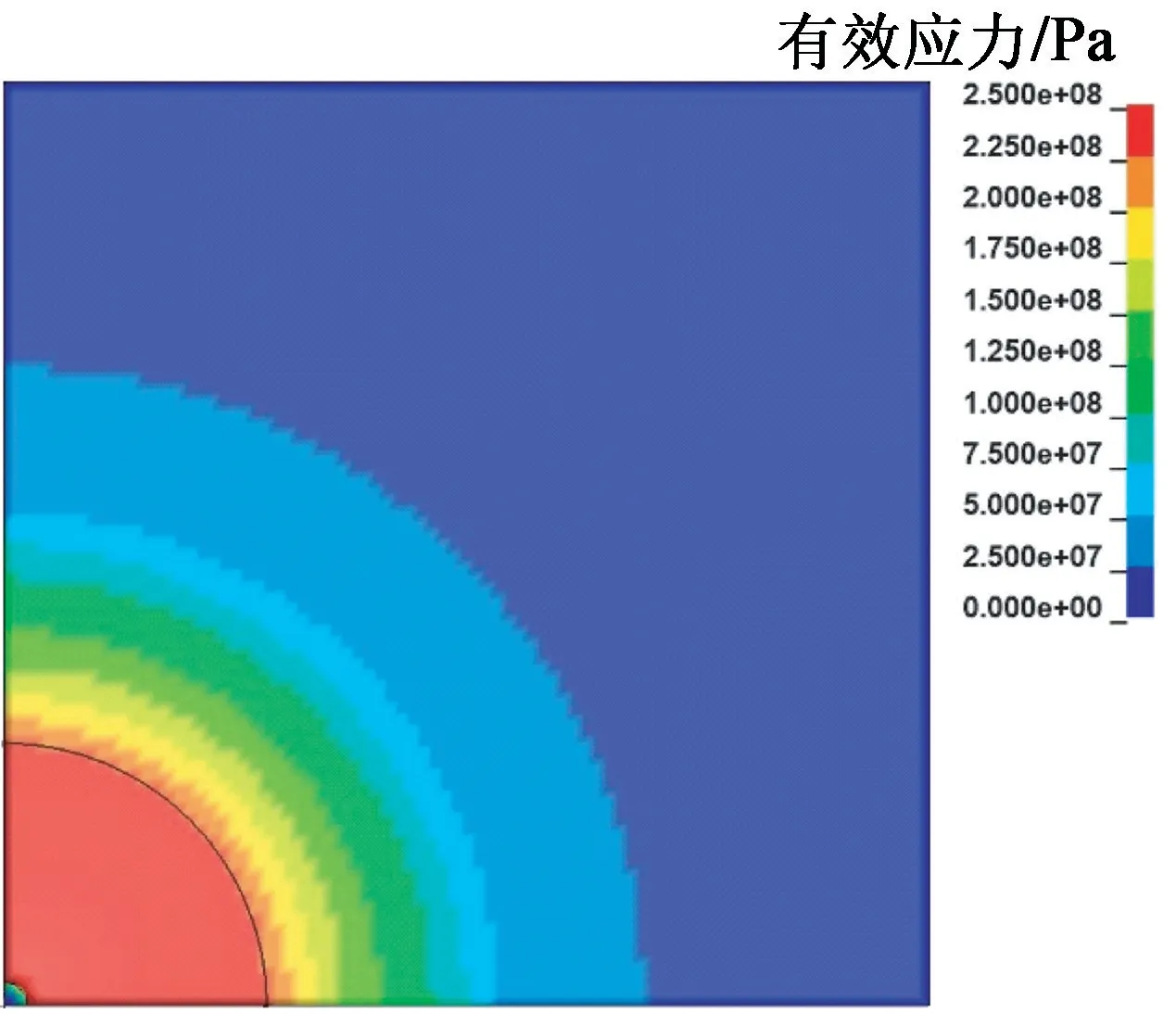
图4 单孔爆破时岩石的应力云图Fig.4 Stress cloud diagram of rock during single-hole blasting

在距离单孔爆破中心0.50、0.75、1.00、1.25、1.50、1.75 m和2.00 m处，分别选择A、B、C、D、E、F、G建立7个单元爆炸的应力输出点。输出点位置及应力变化曲线如图5所示。结果表明:E、F、G点处，单元爆炸峰值应力均未达到岩石抗压强度250 MPa；在距离单孔爆破中心不足1.25 m半径范围内的A、B、C、D 4个点，单元爆炸应力均达到了岩石的抗压强度250 MPa。因此可知，在2＃乳化炸药作用下，单孔爆破的有效爆炸半径范围为1.25～1.50 m，与图4岩石应力云图的有效爆破半径1.48 m相对应。

图5 单孔爆破输出点位置及有效应力变化曲线Fig.5 Output points position and effective stress variation curves during single-hole blasting

3 采石场多孔爆破及布局优化

3.1 多孔爆破理论计算

3.1.1 双孔爆破

1)爆破孔间距。

研究表明，爆破孔间距a的取值范围在R～2R、最小抵抗线W＜R时，双孔爆破裂隙区覆盖了单孔爆破区的所有岩石介质，此时单孔爆破区的面积为S=aW[10]。以最小抵抗线为爆破位置，研究炸药的破坏程度能否满足要求，双孔爆破时应力叠加的最小抵抗线W应低于半径R(图6)。

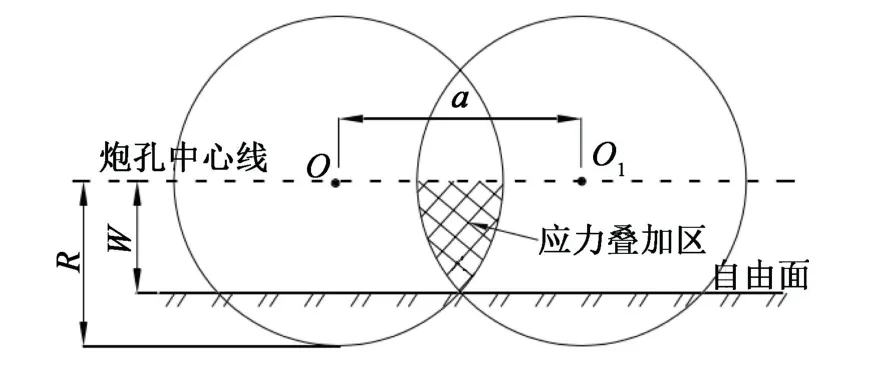
图6 双孔爆破应力叠加图Fig.6 Stress superposition diagram during double-hole blasting

当W＜R＜a时，单孔爆破区的面积为S=aW，双孔爆破破碎区刚好覆盖单孔爆区内的所有岩体，双孔爆破的破碎区叠加消除了破碎力。此时，可认为炮孔爆炸影响区内的岩石均破碎。因此，以S的最大值确定a的值，由几何关系可得a=1.23R；代入有效爆破半径R=1.48 m，则a=1.82 m，故其最小抵抗线距离W=1.175 m。

2)双孔爆破分析。

图7为孔间距1.82 m的双孔爆破应力云图。由图7可知，双孔爆破时，横向最大破碎半径R1在2R～3R之间，单元应力全部达到岩石材料的抗压强度。因此，可以判定，双孔爆破的横向最大破碎有效影响半径约为4.53 m。在双孔爆破中，各炮孔爆破半径内的岩石全部达到了抗压强度，即发生破碎。此外，爆炸应力波导致炮孔叠加区域上方的部分岩石材料达到抗压强度，出现破碎。

图7 双孔爆破时岩石的应力云图Fig.7 Stress cloud diagram of rock during double-hole blasting

3.1.2 多孔爆破半径

1)多孔分布方式。

常用的布孔方式有单排布孔和多排布孔两种[15]。现以多排炮孔布置为研究对象，分别分析双排矩形炮孔布置和双排三角形炮孔布置。当双孔爆破间距为1.82 m时，其爆破范围内所有岩石受到的冲击波均达到破碎要求。为达到最佳爆破效果，分别设置炮孔间距为1.82 m的双排矩形炮孔与孔间距1.82 m、排距为1.57 m的双排三角形炮孔，如图8所示。

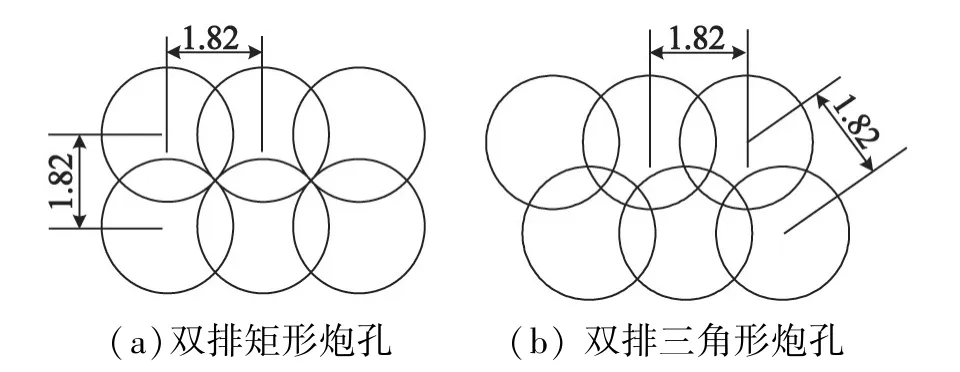
图8 双排炮孔分布示意图(单位:m)Fig.8 Schematic diagram of the distribution of double-row blast holes(unit:m)

2)多孔爆破分析。

由图9可知，双排矩形炮孔和双排三角形炮孔爆破时，各炮孔爆破半径内的岩石应力达到了抗压强度极限，表明在该区域内岩石全部破碎。根据图9(a)可知，爆破影响范围以外，应力逐层降低；受两排端部应力波共同作用，部分区域应力也达到了抗压强度，形成岩石破碎。根据两种排布方式的影响范围，得到三角形分布和矩形分布的双排炮孔爆破有效面积分别为27.43、28.30 m2。由于三角形炮孔分布的排距为1.57 m、矩形炮孔分布的排距为1.82 m，进而导致了双排矩形炮孔布置时有效爆破面积比双排三角形炮孔布置时大3.11%。

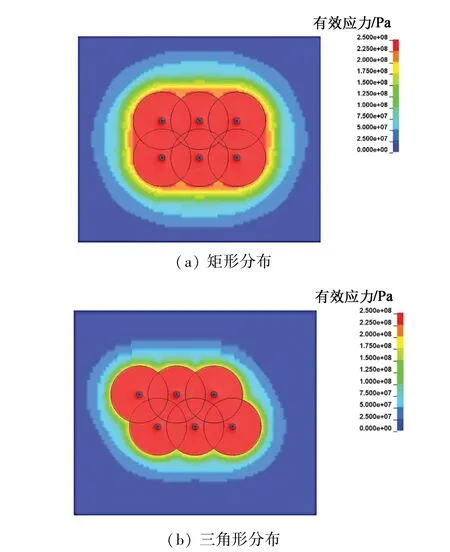
图9 多孔爆破时岩石的应力云图Fig.9 Stress cloud diagram of rock during multi-hole blasting

3.2 多孔爆破数值模拟及验证

3.2.1 双孔爆破

在露天采石场双孔爆破模拟中，沿着双孔爆破中心位置向两边选取距离中心点0.5、1.0、1.5、2.0、2.5 m和3.0 m的6个输出点A、B、C、D、E、F，输出点及应力变化曲线如图10所示。由图10(b)可知，除E点和F点峰值应力小于250 MPa外，A、B、C、D 4个点的峰值应力均达到岩石的抗压强度250 MPa。结果表明，双孔爆破横向最大破碎半径在4～5 m之间，其爆炸应力变化与峰值应力曲线基本一致，验证了孔间距a为1.82 m、有效影响半径R为4.53 m的双孔爆破理论值。因此，该双孔爆破间距的选择较为科学。

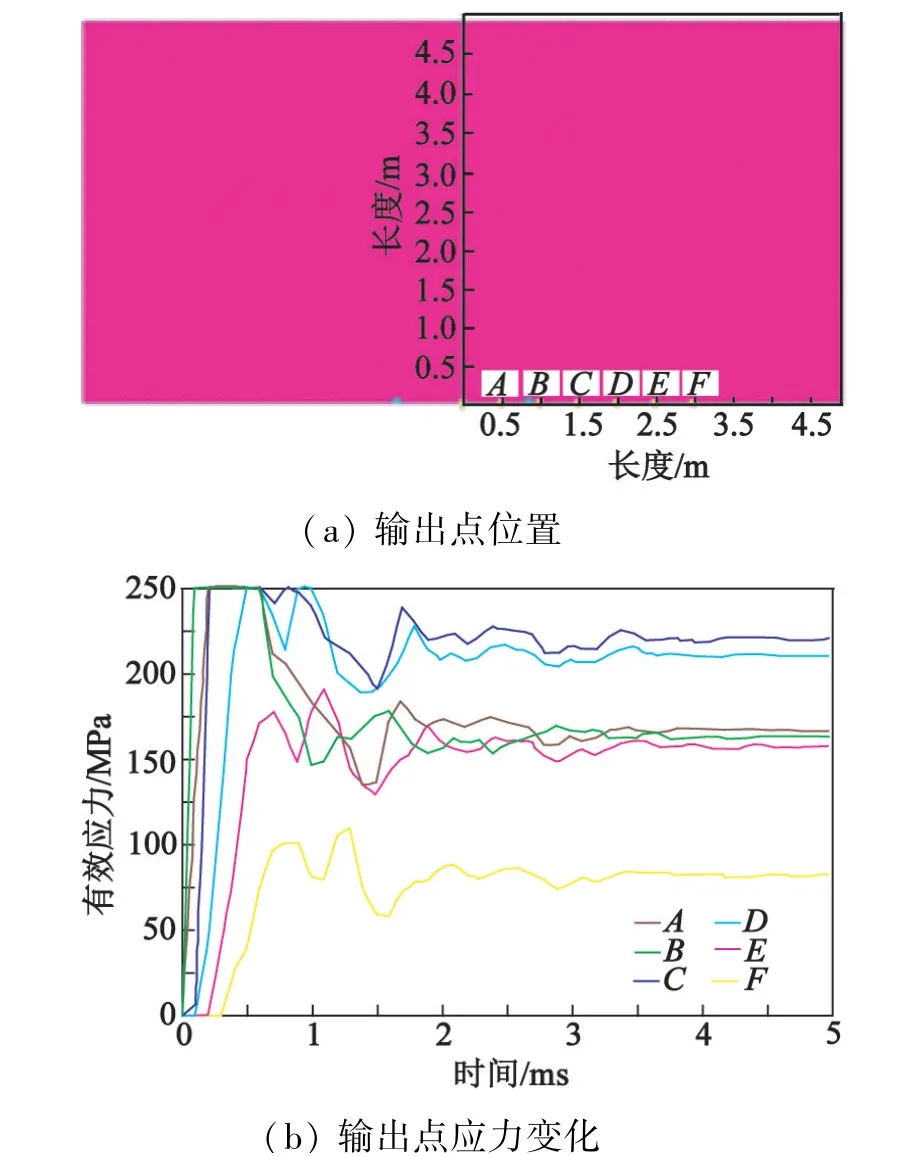
图10 双孔爆破输出点位置及有效应力变化曲线Fig.10 Output points position and effective stress variation curves during double-hole blasting

3.2.2 多孔爆破

分别在双排矩形分布和双排三角形分布中横向选取距离爆破中心0.5、1.0、1.5、2.0、2.5、3.0、3.5 m的A、B、C、D、E、F、G 7个点，如图11所示。岩石应力变化曲线如图12所示。由图11和图12可知，除G点峰值应力未达到岩石的抗压强度，A、B、C、D、E、F 6个点的抗压强度均达到250 MPa，形成了岩石完全破碎。结果表明，多孔爆破双排中心线上的有效爆破范围在3.0～3.5 m之间；在多孔爆破的三角形排布中，3.0 m处的F点应力达到了岩石的抗压强度250 MPa，但与多孔爆破的矩形孔排布中3.0 m处的F点对比，三角形排布的F点应力下降明显。

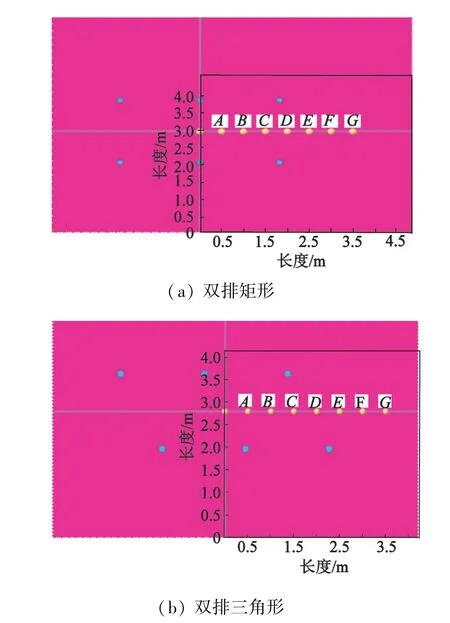
图11 多孔爆破应力测点布置示意图Fig.11 Schematic diagram of layout of stress measuring points during multi-hole blasting

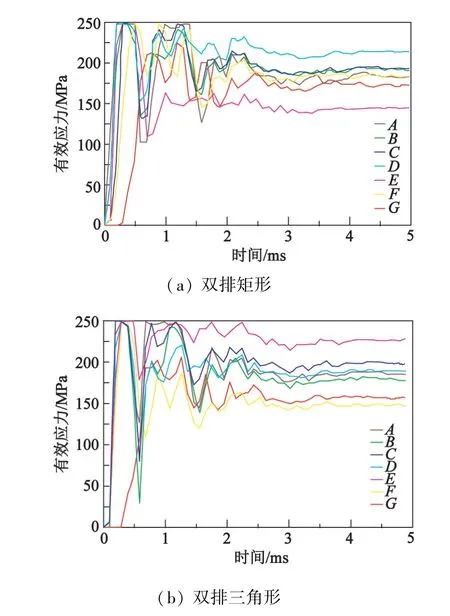
图12 多孔爆破有效应力变化曲线Fig.12 Effective stress variation curves during multi-hole blasting

3.3 采石场爆破作业的炮孔布置优化

3.3.1 炮孔布置优化措施

通过对单孔爆破、双孔爆破以及多孔爆破进行模拟研究与对比分析，结合某露天采石场的工程项目，提出采石场爆破作业的炮孔布置优化措施:

1)露天采石场宜选用双炮孔布置爆破作业。在等同的TNT当量下，双孔爆破时的有效爆破半径为4.53 m，比单孔爆破时的有效爆破半径2.96 m(1.48 m×2)大53.04%。双孔爆破的工程效率明显高于单孔爆破，双炮孔布置爆破作业极大地提高了工程爆破效率，以较低的成本费用提供了同等岩石爆破效果。

2)露天采石场多孔爆破作业宜选择双排矩形炮孔布置。在露天采石场实际工程作业中，双排矩形炮孔的有效爆破面积比双排三角形炮孔大3.11%。矩形炮孔的排布方式可减少露天采石场在开采过程中的钻孔、搬运、储运、火药、人工等费用，保证整体的工程质量与工程效益。

3)露天采石场在特殊情况下采用多孔双排三角形爆破排布方式时，排距应为孔距的3/2倍。采用多孔双排三角形爆破，炮孔排列较为紧密，能较高效地利用乳化炸药的爆炸能量，使岩石开采的欠爆区和过爆区减小。

3.3.2 现场试验

以数值模拟与理论计算的炮孔布置优化措施为依据，孔间距a设为1.82 m，使用2＃乳化炸药分别进行单、双炮孔爆破试验和双排矩形、三角形炮孔试验。将优化后的炮孔布置措施用于现场试验，与优化前的爆破情况进行对比，如图13所示。单孔爆破的有效爆破半径为2.72 m(1.36 m×2)，双孔爆破的有效爆破半径为4.28 m，比单孔爆破时提高了57.36%。双排三角形炮孔爆破的有效爆破面积为26.65 m2；双排矩形炮孔爆破的有效爆破面积为27.48 m2，比双排三角形炮孔爆破时提高了3.11%。炮孔布置优化后，采石场的有效爆破面积得到增大，证实开采炮孔布置优化措施的可行性，提高了采石场的工程效益。