数学建模思想应用于微积分的教学实践
2022-06-21陈梅香谢溪庄
陈梅香 谢溪庄
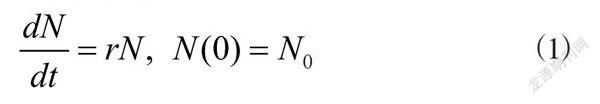

[摘 要] 常微分方程是微积分课程中的重要组成部分,在自然科学和社会科学中有着广泛的应用。针对微分方程教学过程中存在的问题,提出解决的可行性方案,再以可分离变量的微分方程为例,以数学建模思想为导向,将抽象的理论知识附着在实际问题中,让学生在应用的背景中学习、理解可分离变量微分方程的求解及其应用,提高他们学习数学和应用数学的能力。
[关键词] 微分方程;数学建模;可分离变量方程;Matlab工具
[基金项目] 2020年度福建省教育厅境外生公共数学教育教学改革项目(FBJG20200181); 2021年度第三批华侨大学一流本科课程建设项目
[作者简介] 陈梅香(1984—),女,福建泉州人,博士,华侨大学数学科学学院讲师,主要从事数值线性代数研究。
[中图分类号] G642 [文献标识码] A [文章编号] 1674-9324(2022)20-0141-04 [收稿日期] 2021-01-19
高等数学的主要内容是微积分,而微积分是以极限为基本思想和基本运算来研究实数集上的函数[1]。微分方程则是高等数学的重要组成部分,它是数学联系实际,并应用于实际的重要途径和桥梁。在反映客观现实世界运动过程的量与量之间的关系中,大量存在着满足微分方程关系式的数学模型,需要通过求解微分方程来了解未知函数的性态,从而精确地表述事物变化所遵循的基本规律[2,3]。例如:牛顿在研究天体力学和机械动力学时,就利用了微分方程这一工具,从理论上得到了行星的运动规律;法国天文学家勒维烈和英国天文学家亚当斯使用微分方程各自计算出那时尚未發现的海王星的位置等,这些都使数学家和物理学家更加深信微分方程在认识自然、改造自然方面的巨大力量。
数学建模是人们应用数学方法探讨自然现象、社会现象、工程技术以及日常生活中的实际问题的过程,是联系数学与应用的重要桥梁[4,5]。作为数学走向应用的最初一步,事实上,数学建模与数学学科本身有着同样悠久的历史。从古希腊数学家欧几里得的几何原本,到根据大量天文观测数据总结出来的行星运动的三大定律;从牛顿和莱布尼兹创立的微积分,到流体力学以及量子力学中的微分方程,无一不是揭露了事物本质的数学模型。随着计算机技术的发展,数学迅速地进入了自然科学和社会科学的各个领域,为数学建模开拓了广阔的用武之地。将数学建模引入到微积分,尤其是常微分方程的教学中,为数学与外部世界的联系提供了一种更有效的方式。让学生学习和品味数学是如何从实际问题中提炼出来,是如何应用于实际问题的,这也是传统的教学课堂和教材上所缺少的,这必将启迪学生们的数学心智,促使他们更好地学习、理解、应用数学,这对于学生的“学以致用”和“用以致学”都是一件很有意义的事情。
一、高等数学中微分方程课程教学存在的问题
对于非数学专业的学生来说,一般是在学习完一元函数的微分学和积分学后开始接触微分方程。然而,不少同学对微分方程这一知识体系的学习却觉得有些吃力,知识点的理解有些困难,往往只会一些简单方程的计算,而且很多时候也是生搬硬套书上的公式,谈不上对知识点的理解,其主要原因主要有以下三个方面。
(一)很多教材过于理论化、抽象化
数学中的基本概念、基本公式和基本定理大多来源于实际生活中的具体问题,再经过分析、总结,最后用数学语言描述形成数学理论。很多高校都是选用《高等数学》作为非数学专业学生系统学习微积分和微分方程的教材。与更加理论化、专业化的《常微分方程》相比,《高等数学》显得更加简单、系统,而且授课的学时也较少。然而,很多教材在微分方程这一知识体系上的内容介绍过于理论化、抽象化,导入的问题和分析的案例比较陈旧和单薄,与实际应用的关联度较少,这就使得学生对微分方程的学习和理解比较困惑,在脑海中呈现出来的都是如何计算微分方程,只停留在微分方程理论知识的表面,不懂得如何学以致用。
(二)课堂教学上重理论轻应用
在微分方程的课堂教学上很多都是依据教材、按部就班,教学内容过于理论化、公式化,形式化,与实际应用联系不够紧密;教学方法单一,与现代信息技术手段的结合较少,课堂比较枯燥无味;有些教师又过分地依赖于多媒体授课方式,未有足够的时间给予学生思考、理解,有种“学术报告”的感觉。而且,一般在介绍微分方程这部分内容的时候,已临近期末,时间紧,任务重。在教学进度、学习任务各方面的压力下,学生在教学课堂上常常有种“满堂灌、听不懂、很凌乱”的感觉,学习效率低下,整个课堂效果不甚理想。
(三)学生的学习兴趣不浓、积极性不够
高等数学的知识体系是环环相扣、紧密相连的,而知识的学习是一个从接触、学习、巩固、提高到熟练掌握的过程。大一的新生刚从中学过来,对老师的依赖性比较大,习惯了中学期间重复性的做题、训练、讲解,从而完成对知识点的理解和掌握,还未能很好地适应大学的学习生活。对于高等数学的学习,总感觉“概念多、定理多、理论性强、实际应用少”。尤其是进入大学阶段后,整体管理较为轻松,缺乏群体学习的压力和激励,一旦教师授课手段或方式缺乏多样性,学生就容易出现疲倦状态,学习动力不足,学习效果不好。一旦没有微分学和积分学的坚实基础,对于微分方程的学习自然是一头雾水、云里雾里。
二、微分方程教学中融合数学建模思想的思考
高等数学内容丰富,难度大,课时少,需要学生有着更高的理解、分析和逻辑推理能力。同时,作为教师则需要帮助学生转变学习方式,帮助他们从“被动学习”到“主动学习”。微分方程作为微分学和积分学在理论上的推广及应用,在很多学科领域都有着重要的作用,是研究和解决很多实际问题的有力工具。下面以可分离变量的微分方程为例,结合笔者多年来在高等数学与数学建模的教学经验,对数学建模思想应用于微分方程教学提出如下可供参考的建议。
(一)源于教材,高于教材
现有微积分教材中关于微分方程知识体系,虽有着内容的完整性和理论的严谨性,但较为抽象,案例较为陈旧。在教学过程中,应以数学建模思想为导向;以学以致用、用以致学为目标;对理论知识进行探究、再加工;使之简单化、易理解。可以寻找一些与知识点相关,又源于生活、生动新颖,内容丰富、启示性强的案例进行建模示范,将抽象的理论附着在现实的背景中,让学生在应用情境中认识微分方程、学习和掌握微分方程的理论及其应用。
(二)活跃课堂教学,提高课堂效率
在课堂教学中,根据引入的实际案例,设置悬念、创设问题情境、让学生参与讨论、引导学生思考问题、解决问题,激发学生的学习乐趣。此外,还可分享一些理论知识背后的历史背景和数学家故事,消除课堂教学上的疲倦感,缓解理论学习的压力,培养他们追根溯源、发散思维的能力。
(三)借助Matlab工具和数形结合思想,提升直观想象能力
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,分析研究对象的性质及变化规律。通过图形构建数学问题的直观模型,将数学理论知识的呈现可视化,进而探索、发现并解决问题,这是学习数学和应用数学的很有效方法。同时,这也需要在课堂教学上整合信息技术、数学软件、数学模型等多种资源,丰富课堂教学方式,使学生从感官上获得认知,内化为对实际问题的理性思考。其中,Matlab工具在理论知识的可视化,提升学生直观想象能力等方面都扮演着很重要的角色。Matlab作为方便使用、功能强大的数学软件之一,具有强大的数值运算和图形可视化功能。尤其在微分方程方面,Matlab不仅可以求解微分方程的解析解,还可以求解微分方程的数值解、估计方程中的参数、检验微分方程与实际数据的吻合情况以及实际问题的仿真。当然,它还可以很轻松地将微分方程中蕴含的解函数以二维图形或三维图形的形式呈现出来。这样,不仅可以把很多实际问题和研究对象变得具体化、形象化,使学生从复杂的数学理论的理解转化为对图形的理解,加快、加深学生对知识点的学习、理解及应用,丰富课堂教学内容,调动学生的学习积极性,进一步地培养学生的观察、分析、直观想象的能力。
三、情景再现——实例分析
函数刻画的是事物间的相关性,是用來描述“关系”或“变化”的工具。而导数是研究函数增减、变化快慢的最有效的工具,通俗地讲是研究某个变量相对于另一个变量变化的快慢程度。微分方程则是联系自变量、未知函数及其变化率(导数)的关系式。事实上,微分方程是一个数学建模的过程,是一个源于实际,应用于实际的一个重要数学工具。它能够较好地捕捉一些实际问题中蕴含的变量之间的联系,进而形成微分方程这一数学语言,只要求出这一方程的解函数或获得解函数的性态,便可获悉该实际问题背后的自然规律,帮助人们解决实际问题。下面,我们以人口模型为例,结合Matlab工具的数值分析,以期让学生在具体的应用情境中学好可分离变量微分方程的计算、求解及应用知识。
(一)问题的引入
有个地区,人口的相对增长率是个常数,即单位时间内人口的增长量与人口成正比,假设这一比例系数为r,那么该地区人口数量随时间是如何变化的?
(二)数学模型
①建立微分方程:假设该地区初始时刻的人口为N(0)=N0,时刻t的人口为N(t),那么在时刻t到t+Δt这段时间内人口的增长量为:N(t+Δt)-N(t)=rN(t)Δt,上式两端同除以Δt并令Δt→0时,可得如下微分方程:
(1)
②引入可分离变量微分方程的求解:在自然科学和社会科学各个领域有一类常见的方程,其形式如下:
g(y)dy=f(x)dx, (2)
我们称之为可分离变量微分方程。
提问:这样形式的微分方程有什么特征?
对于可分离变量方程,可知其解等价于积分方程的解(详见文献[1-3],在板书上详细推导),因此只需求出g(y)和f(x)的原函数,即可得到方程(2)的通解。若方程(2)还满足初始条件,便可进一步得到该方程的特解。
③模型的求解和Matlab数值分析:方程(1)显然是一个可分离变量方程,经变量分离并对方程两边取不定积分后可得:N(t)=N0ert。
讨论:这个函数关系式能说明什么现象,揭示什么规律?
这个函数关系清晰地表明了人口数量与时间的变化关系。借助Matlab工具,取N0=30.6,r=0.02,可在平面上画出人口数量关于时间的函数曲线。不难看出,人口数量呈现出指数增长的变化趋势,而且每34.6年会增加一倍。
④背景知识和历史的检验:方程(1)就是经典的马尔萨斯人口模型,最早由英国著名的人口学家马尔萨斯在1798年提出。他在担任牧师期间,查看当地一百多年的人口出生资料发现了一个规律:该地区人口的相对增长率是个常数,便建立该模型,用以分析人口数量的变化情况。与历年的世界人口统计资料对比,可发现人口增长的实际情况在一定时期内与马尔萨斯模型预报的结果是基本相符的。例如,1961年世界人口数为30.6亿,人口增长率约为2%,人口数大约每35年增加一倍。检查1700年至1961年的260年人口实际数量,发现两者几乎完全一致。
(三)模型的改进
①新问题:按照马尔萨斯人口模型,人口数量将呈现几何级数的方式增长。可以计算到2510年,人口将达到2×1014,这是不现实的,因此模型(1)在人口数量不太大的时候是合理的,而长时间来看,又是不吻合的。随着人口的增加,自然资源、环境条件等因素会对人口继续增长的阻滞作用越来越显著。
②新模型:因为人口增长率会随着人口的继续增加而减少,一个简单的方法是将增长率看成N(t)的一次函数,即如下新模型:
(3)
这里r表示自然增长率,表示资源环境阻滞人口增长,Nm表示环境容纳量。
③新模型的求解和Matlab数值分析:方程(3)仍是一个可分离变量方程,这个方程也称为Logistic模型。经变量分离求解可得:
(4)
该函数清楚地揭示了人口数量与时间的变化关系。借助Matlab工具,记1961年为t=0时刻,即N0=30.6亿,并取r=0.0243,Nm=150亿,可在平面上画出人口数量关于时间的函数曲线,不难获悉人口数量随着时间的变化先是指数上升,后来则趋于平稳,说明人口数量不会无限制地增长。
④真实数据的检验:取t=39和t=59时,分别对应于2000年和2020年,根據函数关系(4)式可求得N(39)=59.7,N(59)=77.7,即2000年和2020年世界人口数量分别为59.7亿和77.7亿,这与联合国人口基金会发布的世界人口报告中的61.14亿和77.62亿是基本一致的。
结语
为了让学生领悟高等数学的本质及应用的精髓,激起学生学习数学的兴趣和积极性。本文从微分方程教学过程中出现的问题出发,结合笔者多年来的高等数学和数学建模教学、辅导经验,提出将数学建模思想融合于微分方程的教学中。并通过具体的人口实例,充分利用数学建模的方法,让学生清晰地看到微分方程可以从哪里来,如何分析、求解,又如何回到实际问题中,也让学生明白微分方程不只是一个计算的过程,而是一个数学建模的过程,可以很好地应用于我们日常生活中的许多问题,并逐渐地理解微分方程研究的目标是微分方程驱动下的函数性态和函数曲线规律,而不单纯地是一个抽象的数学概念。
参考文献
[1]同济大学数学系.高等数学[M].7版.北京:高等教育出版社,2014:297-307.
[2]王高雄,周之铭,朱思铭,等.常微分方程[M].3版.北京:高等教育出版社,2006:30-42.
[3]东北师范大学数学系.常微分方程[M].3版.北京:高等教育出版社,2005:1-17.
[4]姜启源.数学建模案例精选[M].北京:高等教育出版社,2017:1-27.
[5]谭忠.数学建模:问题、方法与案例分析[M].北京:高等教育出版社,2018:137-155.
Application of Mathematical Modeling Idea in Calculus Teaching Practice: Taking the Differential Equation of Separable Variables as an Example
CHEN Mei-Xiang, XIE Xi-zhuang
(School of Mathematical Science, Huaqiao University, Quanzhou, Fujian 362021, China)
Abstract: The ordinary differential equation is an important part of Calculus, which is widely used in natural science and social science. In this paper, we present the feasible solutions for the problems in ordinary differential equation teaching. Furthermore, taking the variable separable differential equation as an example, we focus on how to apply the practical problems into the abstract mathematical theoretical knowledge guided by the idea of mathematical modeling, which can make students study better in this environment and understand the solving of variable separable differential equations. Meanwhile, it can improve students’ ability to study mathematics and apply mathematics.
Key words: differential equation; mathematical modeling; variable separable differential equations; Matlab tools
