含风电场的可用输电能力改进布谷鸟算法

李 辉,朱军飞,陈 浩,蒋东荣,曹天蓝，张昭阳

(1.国网湖南省电力有限公司， 长沙 410000；2.重庆理工大学 电气与电子工程学院， 重庆 400054)

0 引言

可用输电能力(available transfer capability，ATC)表示在传输网络安全、稳定状态下的电力市场交易量的最大值。随着电力交易的市场化，ATC成为电力交易参与者在签订输电协议时必须了解的重要信息。由于以风电为代表的分布式能源并网规模越来越大，电网中不确定性因素越来越多，使得ATC计算愈发困难，如何快速、准确地求解ATC成为当下研究的重点[1]。

通常，ATC研究方法可分为确定性方法和概率性方法。ATC的确定性研究方法忽略了系统中大多数不确定性因素，计算速度快，易于实现，但计算结果相对保守[2-3]；概率性研究方法能充分考虑系统中各种不确定性因素的影响，更符合系统实际运行情况，但计算速度慢[4-5]。随着风电并网规模不断扩大，电网中不确定性因素越来越多，因此ATC的概率性研究方法更适合电网实际运行情况。对于风电并网系统的ATC计算，目前已有一些研究成果。周明等[6]和陈厚合等[7]研究了风电并网方式、位置和容量变化对ATC的影响，但由于风速样本基于蒙特卡罗法产生，采样时间较长；楚云飞等[8]采用无迹变换采样，缩短了风速采样时间，虽然能极大提高ATC求解效率，但会带来一定误差；罗钢等[9]采用拉丁超立方采样法考虑风电场空间相关性，可以在大量场景下快速地计算ATC，但未考虑风速时间相关性的影响；陈金富等[10]建立了含机会约束规划的风电场ATC模型，将机会约束模型转化为等价的线性潮流模型，简化计算的同时提高了ATC计算速度，但计算结果稍显保守。综上，含风电场的ATC评估需考虑多种因素影响，而现有研究大都通过降低计算精度换取更快的求解速度，从而满足ATC在线评估要求。本文中主要通过风电相关性来验证改进算法对风电并网系统ATC计算的影响。

ATC计算属于多约束求解问题，而最优潮流法(optimal power flow,OPF)可以灵活处理系统中各类约束，合理分配电网资源，适合大规模系统的ATC求解。通过在OPF模型中引入数理统计方法，概率OPF模型能够更好地计及系统中的不确定性因素。汪峰等[11]建立了基于OPF的ATC计算模型，提出了6种等效且可行的目标函数，为ATC研究提供了重要理论支持。OPF模型求解可采用传统算法，如内点法[12]、牛顿法[13]和Benders分解法[14]等，这些算法各有优势，但它们都通过一个点进行反复迭代计算，跳出局部最优的能力差，难以保证计算结果的有效性，且当系统规模较大时，计算速度慢。元启发式算法引入了种群概念，让种群中多个个体共同寻优，有更好的鲁棒性和全局寻优能力。一些元启发式算法已应用于ATC计算中，如遗传算法[15]、粒子群算法[16]、人工鱼群算法[17]等，但这些算法都存在易陷入局部最优或计算时间长的缺点。

布谷鸟搜索算法[18](cuckoo search，CS) 作为一种新的元启发式算法，其特有的发现概率能有效地帮助跳出局部最优值，且需要调节的参数少，操作简单，特别适用于处理大型系统连续优化问题。为此，本文中保留CS算法的优势，构建基于动态发现概率与混沌差分变异的改进布谷鸟搜索算法(improved cuckoo search，ICS)，解决含风电场的ATC计算问题。

1 风电场出力采样

1.1 风电场随机出力模型

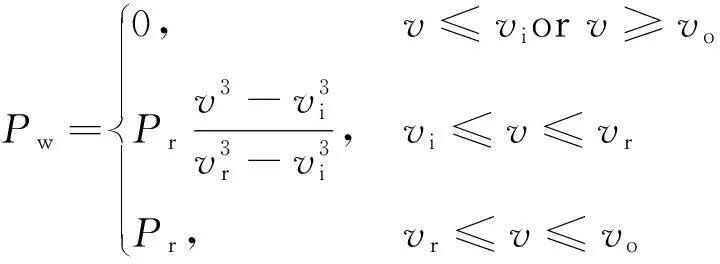
由Weibull分布表示的风速表达式见式(1)。通过式(2)将风速转换为风电出力[19]。

(1)

(2)

式中：v为风速；k为形状系数；c为尺度系数；Pr为风机的额定功率；vi、vr和vo分别为切入风速、额定风速和切出风速，共同决定了风电出力的上、下限。

1.2 基于拉丁超立方采样法的相关性采样矩阵

由于风速具有波动性，直接将其随机出力值代入系统进行计算会导致波动过大，严重影响系统稳定性，且大量风速数据的引入会导致ATC计算速度极慢。风速的相关性也会影响最终采样值。因此，在计算前要对风速进行相关性采样，降低计算规模。拉丁超立方采样法[20]可通过排序获得具有相关性的采样样本，具体过程如下：

1) 获得风速累积分布函数：

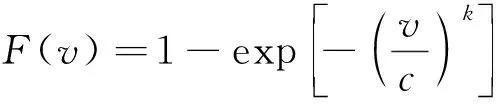
(3)

2) 将F(v)平分为N个子区间，选取每个子区间的中值作为采样点，逆变换得到初始采样矩阵。

3) 采用秩相关系数ρ表征任意2个随机变量的相关性：

(4)

式中：w1,w2是2个随机变量的秩；cov(*)表示协方差；σ(*)表示标准差。

4) 生成2×N阶随机排列正整数矩阵R，并计算秩相关系数矩阵ρ1；对ρ1进行Cholesky分解得到下三角矩阵C。

5) 根据历史采样数据获取2个目标随机变量的秩相关系数矩阵ρ2；按照同样的操作得到下三角矩阵Q。通过L=QC-1R求得排序矩阵。

6) 按排序矩阵中行数字大小对初始采样矩阵进行排序，得到最终采样矩阵。

2 ATC的最优潮流模型

在基态潮流的基础上，同时增加送电区域发电节点出力和受电区域负荷功率，并保证其他发电节点出力和负荷节点功率不变，直到出现安全约束越限，此时受电区域的临界负荷减去基态功率即为两区域间的ATC。本文中采用OPF建立基于静态安全约束的ATC模型。

1) 目标函数为：

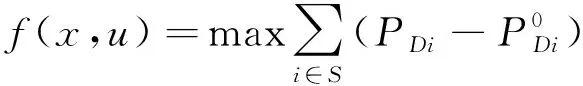
(5)

式中：S为受电区域节点集合；PDi为节点i上有功负荷，上标0表示其基态负荷；x为控制变量，包括发电机出力和发电节点电压幅值；u为状态变量，如节点有功负荷、受电节点的幅值、相角等。目标函数表示受电区域内有功负荷可增加量总和的最大。

2) 约束条件。考虑风电出力的节点功率平衡方程为：

式中：Pwi、Qwi分别为风电场的有功出力、无功出力，通过1.1节的采样方法得到；PGi、QGi、PDi、QDi分别为节点i上发电机有功出力、无功出力及有功负荷、无功负荷；Vi是节点i的电压幅值；Gij、Bij分别表示支路ij的电导、电纳；θij为节点i、j间的相角差。以下标max、min分别表示值对应的上、下限。

节点电压安全约束为：

Vi,min≤Vi≤Vi,max

(7)

发电机出力约束为：

(8)

线路传输功率约束为：

0≤Sij≤Sij,max

(9)

式中：Sij是支路ij传输的视在功率。

交易约束为：

(10)

上述约束条件中，式(6)为等式约束，式(7)—(10)共同构成不等式约束。

3 基于ICS算法的ATC求解

3.1 标准布谷鸟算法

CS算法通过大步长和小步长交替进行的莱维飞行机理找寻最优解，具有良好的全局寻优能力。除种群大小和最大迭代次数外，CS算法需调节的参数只有发现概率pa，而pa并不会影响收敛速度。故CS算法具有参数少、操作简单、全局搜索能力强的优点。其个体更新方式有2种：

1) 基于莱维飞行更新

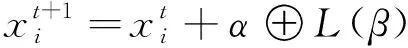
(11)

文献[21]中采用式(12)更新L(β)。

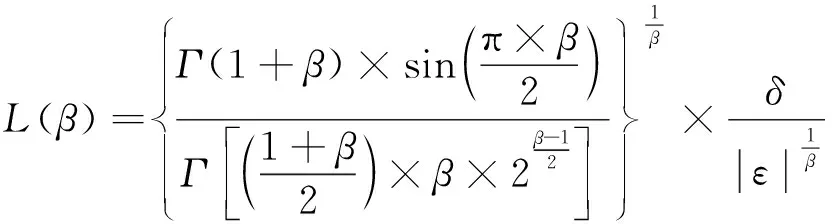
(12)

式中：ε、δ均服从标准正态分布；β取[1,2]范围的常数。

2) 基于发现概率pa更新

生成随机数，若大于pa，则更新位置；否则，保留最优鸟巢，更新公式为：

(13)

式中：η、γ均服从(0,1)均匀分布；当pa-γ>0时，H(pa-γ)为0，否则取1；i、j、k表示互不相同的个体。

3.2 基于混沌差分变异与动态发现概率的ICS算法

由于CS算法在后期收敛慢、易陷入局部最优，故针对CS算法的不足构建ICS算法。做出改进如下：

1) 混沌初始化鸟巢位置，提高前期寻优能力。采用传统方法随机生成初始种群，导致初始解分布不均匀、种群质量低，不利于寻优。利用混沌原理的随机性、遍历性和规律性初始化种群，使初始解均匀分布，种群多样性更高。采用logistic映射进行混沌初始化：

yi+1=μyi(1-yi)

(14)

式中：μ∈(0,4]为控制变量；yi表示第i个鸟巢在混沌空间中的位置，在[0,1]范围取值。

2) 采用动态发现概率，避免算法早熟。随着迭代的进行，个体的质量逐渐提高，在寻优后期易变为局部最优解。因此pa应随着迭次进行而减小，避免算法陷入局部最优。更新公式为：

(15)

式中：pa,max、pa,min为发现概率的控制参数；t为当前迭代次数；tmax为最大迭代次数。

3) 引入差分进化算法的变异环节，进一步增加种群多样性，提高算法后期收敛速度。采用的变异机制：在找到最优鸟巢后，对最优鸟巢进行变异操作，并比较变异前、后鸟巢的优劣。变异公式为：

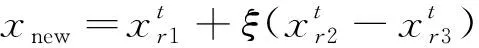
(16)

式中：r1,r2,r3∈{1,2,…,n}且r1≠r2≠r3≠i；ξ∈[0.5,1]，为缩放因子。

3.3 ICS求解ATC流程

步骤1输入系统参数，利用节点功率方程计算基态潮流，并进行混沌操作：设鸟巢个数为n，在混沌空间中随机生成第一个鸟巢位置y1，按式(14)进行n-1次迭代，得到剩余n-1个鸟巢位置；再由式(17)将鸟巢位置映射到搜索空间，作为迭代初值：

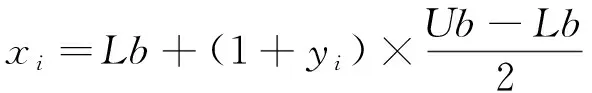
(17)

式中：Ub、Lb表示搜索空间的上、下限；xi为第i个鸟巢在搜索空间的位置，i=1,2,…,n。

步骤2处理约束条件以构建适应度函数(18)，通过潮流计算得到适应度值，用适应度值标识当前解的优劣。约束条件处理：等式约束可通过潮流计算消去，不等式约束采用罚函数法处理。

Fitness(x,u)=-f(x,u)+h(t)p(x,u)

(18)

(19)

步骤3基于莱维飞行和发现概率生成新解，计算并比较适应度值，将最小适应度值对应的鸟巢设为当前最优鸟巢。

步骤4对当前最优鸟巢进行变异操作，将变异前后适应度更小的鸟巢作为本次迭代的最优鸟巢，此最优鸟巢将保留到下次迭代计算。

步骤5判断是否满足终止条件，若不满足则返回步骤3；否则，停止算法。

ICS算法求解ATC的流程见图1。

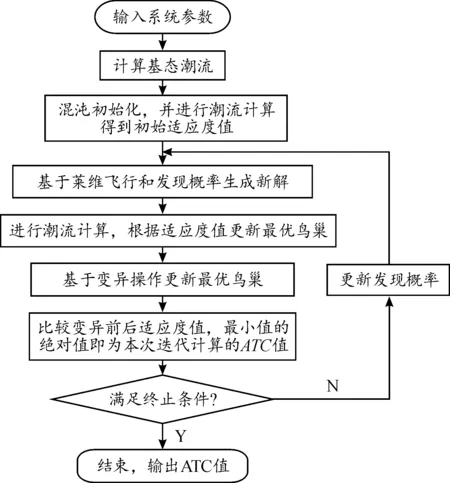
图1 算法流程框图

4 算例分析

采用IEEE-30标准节点系统进行算例仿真，IEEE-30节点系统见图2。系统中共6台发电机，基准功率为100 MW。算法的参数设置如表1所示。发现概率pa的取值范围在[0,1]，由于其取值大小不会影响算法的求解速度，因此pa通常取较小值以提高算法寻优能力。

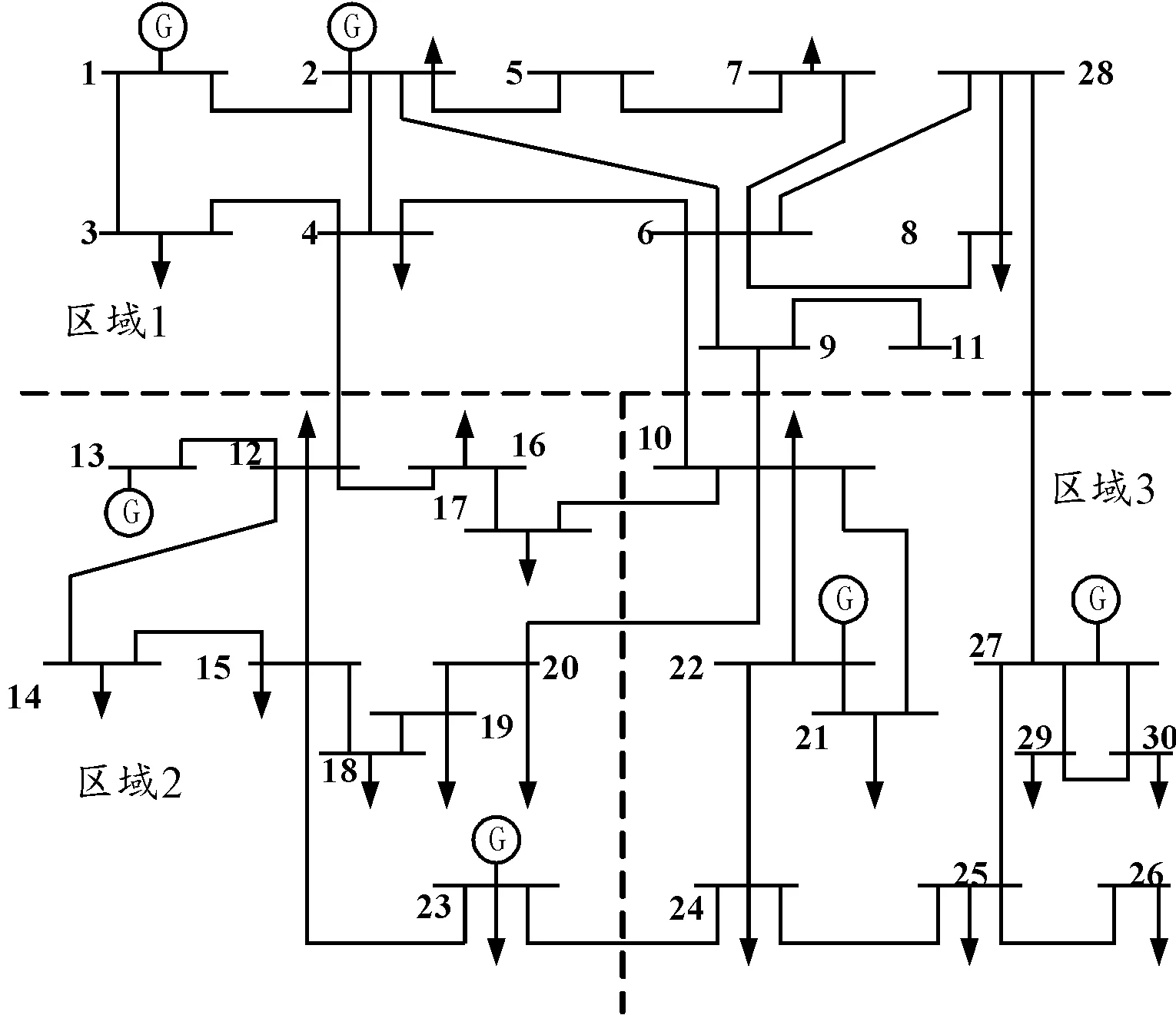
图2 IEEE-30节点系统

表1 算法参数表

4.1 ATC计算结果

采用改进粒子群算法(IPSO)[17]和改进人工鱼群算法(IAF)[18]、CS算法和ICS算法计算不同区域间的ATC值(表2)。记录30次计算的算数平均值。

表2 不同算法下的ATC值

由表2可以看出，IPSO算法在区域3-2已陷入了局部最优解，且综合求解效率低于ICS算法；而IAF算法在区域3-1、区域2-3、区域3-2求出的ATC值高于ICS算法，但在求解速度上，IAF算法计算时间为121.12 s，计算速度较为缓慢；ICS算法求解各区域间ATC效果都不错，计算时间仅为16.47 s，特别是求解区域1-2间ATC时效果显著。限于篇幅，后文仅列出区域1-2间ATC计算结果。

图3为部分算法收敛曲线，通过对比分析发现：IPSO算法的收敛性能是最好的，但易陷入局部最优点，计算结果较为保守；IAF算法会逐步逼近最优值，但收敛速度较慢；CS算法具有较强的全局寻优能力，但会导致后期收敛速度慢、精度低；而ICS算法采用混沌初始化进一步提高前期全局寻优能力，又利用动态发现概率和差分进化算法中的变异算子克服基本CS算法后期收敛慢的缺点，更适合于ATC问题的求解。

表3比较了ICS算法和CS算法的概率评估指标。可以发现，改进后的算法可以提高ATC期望值、最大/最小值，并能显著降低方差，提高系统稳定性。

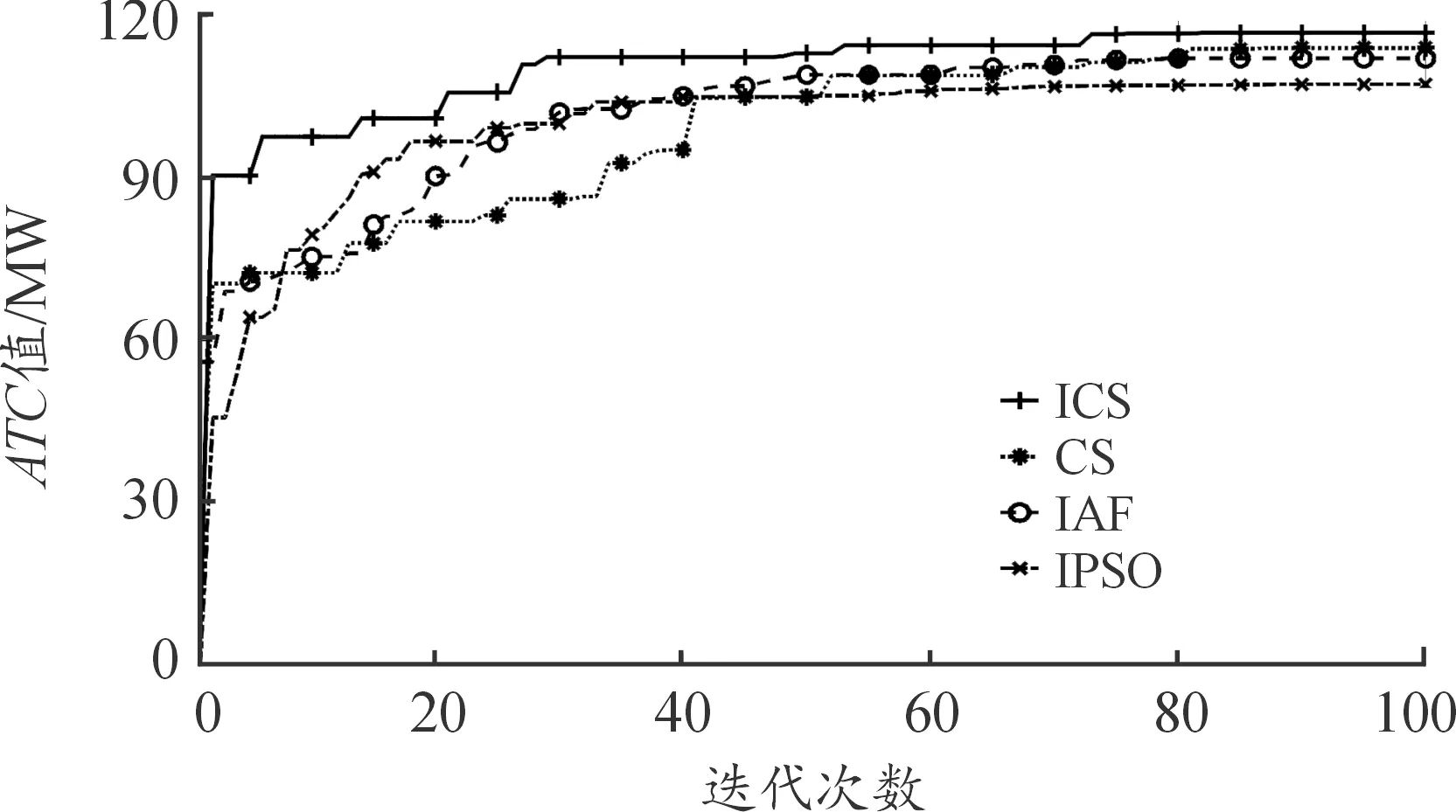
图3 部分算法收敛曲线

表3 ICS算法和CS算法的计算结果

为确保系统的安全性，需进行N-1线路故障分析。断开后会引起系统解列的线路不参与故障分析。取所有N-1故障状态下的ATC最小值为最终决策结果，并将此决策值对应的故障状态作为关键故障，此时的越限支路和越限节点就是系统正常运行模式下的关键约束。相关计算结果见表4。

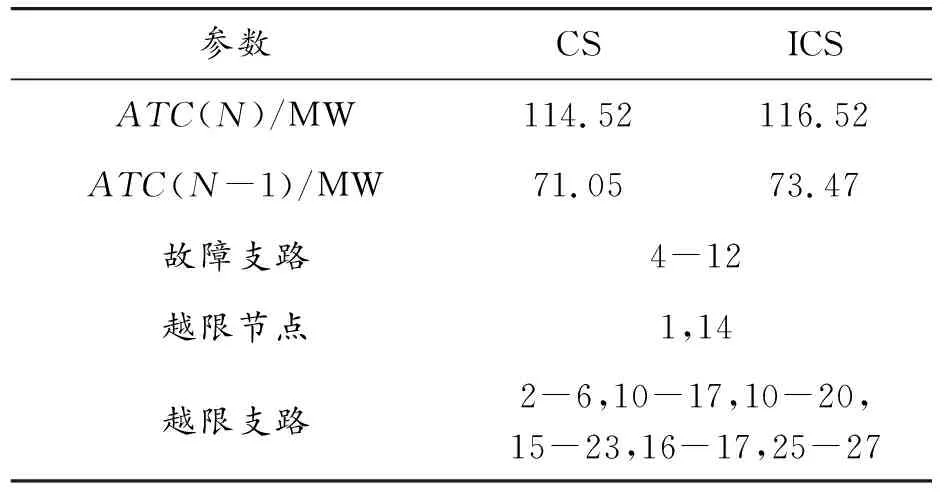
表4 N-1故障下区域1-2的ATC计算结果

通过表4可以找到送受电区域为1-2时的关键约束。同理，可找到其他送受电区域组合的关键约束。这类关键约束关系到系统的安全稳定性，会严重制约ATC。改善这些关键约束能有效提高系统的输电能力，避免输电阻塞。从表4还可看出，只计及N安全约束的ATC计算较为乐观。当考虑N-1约束时，ATC值会明显下降，不利于系统的安全性，因此在实际应用中必须考虑N-1安全约束。本文中，仅需研究风电场对ATC影响的变化趋势，故只进行N安全约束分析。

4.2 风电场对ATC的影响

考虑风电不确定性的影响，并入风电场进行仿真。风机参数设置：k=8，c=2，切入、额定、切出风速分别为3.5 、13 、25 m/s，单个风机输出功率为500 kW。在不同区域接入额定容量10 MW的风电场，ATC评估结果见表5。

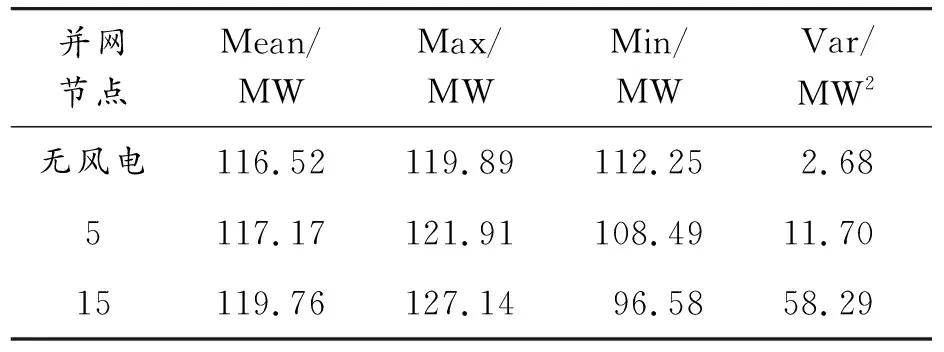
表5 风电不同并网位置时的ATC评估结果

上述结果表明，只要并入风电场，ATC的方差和期望值都会增加。在送电区(节点5)并入风电场，ATC期望值只会略微增大；而在受电区(节点15)并入风电场，ATC期望值增加会更明显。这是因为在送电区域加入风电场，由于送电区负荷并未饱和，风电出力会优先供应本区域内的负荷，对外传输容量的增加并不明显；而在受电区并入风电，风电会供应部分受电负荷，负荷的可增加量就会上升，ATC显著提高，但方差也会极大增加。为保障系统稳定性，在送电区并入风电场更为合适。

为研究风电场相关性的影响，在送电区节点5和7处各并入10 MW的风电场。在满足实时计算要求的前提下尽可能拟合实际情况，采用拉丁超立方采样生成1 000个含相关性的场景集。调节两风电场相关系数进行ATC计算，结果见表6。相关数据表明，风电场相关系数会对ATC计算结果产生影响；随着相关性的加强，ATC的均值会逐渐降低，而方差会先增后减，在相关系数为0.5左右时对系统稳定性影响最大。采用核密度估计法绘制不同相关系数下的ATC计算拟合概率分布曲线(图4)。可以发现，随着相关系数从0.5开始逐渐减少，ATC计算结果会越来越集中于中间区域，曲线也越来越近似于正态分布。根据表6中方差增减规律，相关系数从0.5开始增加时，其分布曲线会以同样的趋势改变。因此在含风电场的ATC计算中，应适当考虑其相关性，以确保分析结果的准确性。

表6 不同风电相关系数下的ATC评估结果

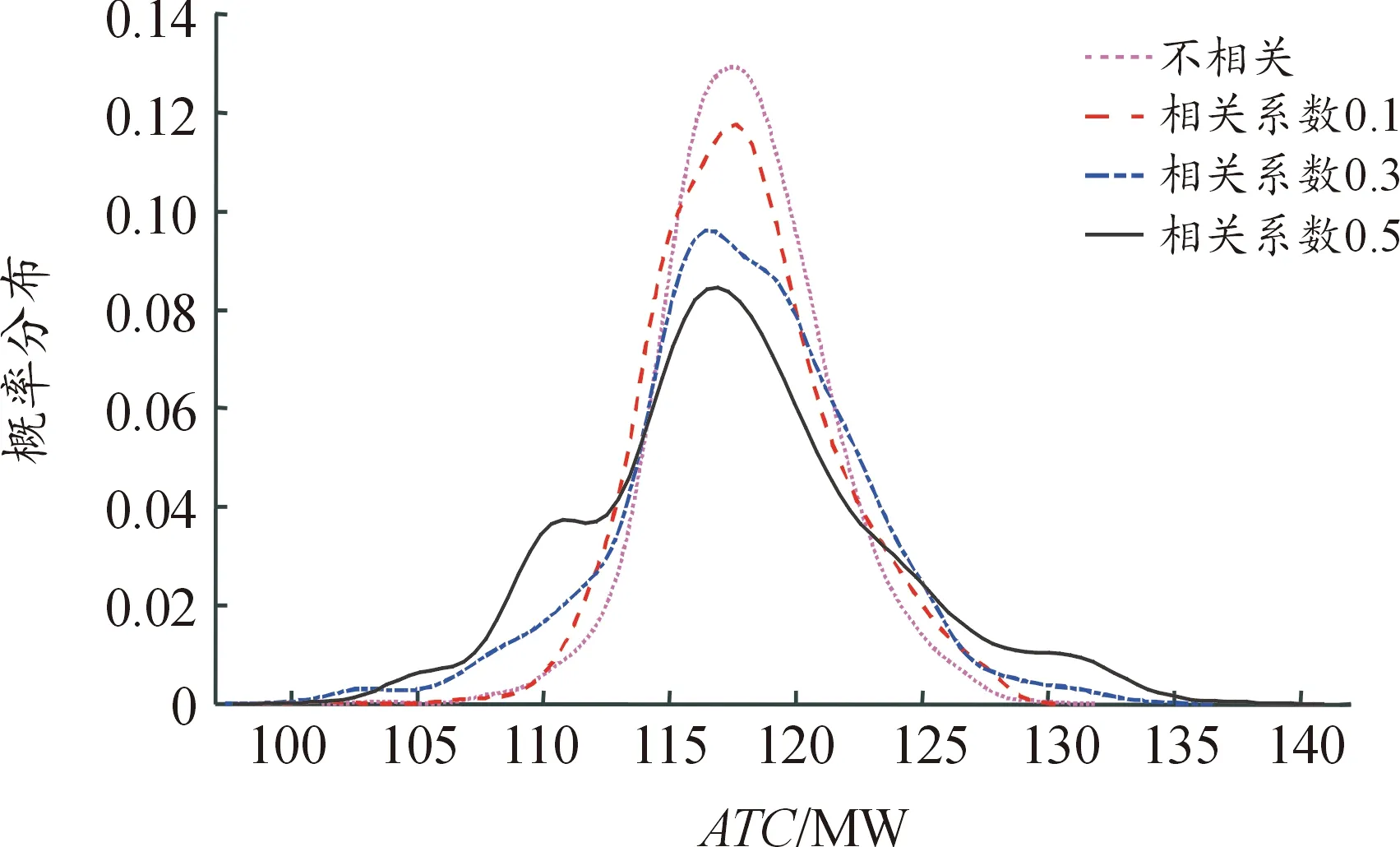
图4 不同相关系数下的ATC拟合概率分布曲线

5 结论

为保证ATC评估的实时性和有效性，构建ICS算法。采用混沌初始化获得更强的前期寻优能力，并利用动态发现概率和变异算子避免早熟，提高寻优精度。同时考虑风电的不确定性，分析风电并网位置和相关性对ATC的影响。通过IEEE-30节点系统验证了改进算法在风电并网系统ATC计算中的有效性、可行性与实用性。由于仅考虑了风电这一不确定性因素，因此多种不确定性因素共同作用对ATC的影响还需进一步研究。