具有不确定参数的耦合神经网络固定与预设时间二分同步
2022-06-18王陆翔刘小洋
王陆翔,刘小洋
(江苏师范大学 计算机科学与技术学院, 江苏 徐州 221116)
0 引言
神经网络是从人脑神经元抽象得来的算法模型,由于其具有分布式计算、自适应、逼近复杂函数等能力,广泛应用于经济、医学、控制以及信息等领域[1-3]。同步是一种典型的动力学行为,它是指系统状态随时间变化趋于一致。其中,耦合神经网络(CNNs)的同步因其在知识工程、图像加密、信息科学等领域的广泛应用备受研究者关注[4-7]。目前,常见的同步类型有完全同步、滞后同步、反同步等[8-10]。
在神经网络同步过程中,受到外部干扰与不确定参数的影响几乎是不可避免的。这可能会造成神经网络不稳定或出现混沌现象。因此有必要探究不确定参数与外部干扰对CNNs同步行为的影响。例如,Zheng等[11]基于间歇牵制方法,解决了具有不确定参数的CNNs的鲁棒同步问题。
在上述同步研究中,所设计的控制算法仅能保证渐近同步,只有当时间趋向于无穷大时系统才能到达完全同步。但是在实际工程应用中,具有较快收敛速度的控制系统拥有更大的应用优势,因此学者们开始研究有限时间同步问题。与渐进同步相比,有限时间同步具有更快的收敛速率、更高的控制精度以及更强的鲁棒性与抗干扰性。梁军丽等[12]设计了非连续控制协议来解决切换CNNs的有限时间同步问题。尽管有限时间同步具有许多优点,但其同步时间严重依赖于系统的初始状态。鉴于此,Polyakov[13]首次提出了固定时间稳定性的概念,其收敛时间不再依赖于系统初始状态。后来,Zhu等[14]讨论了具有外部扰动的CNNs的固定时间同步问题。虽然固定时间控制的同步时间独立于系统的初始值,但想要在预设的时间内达到同步,设计者必须经过复杂的计算来调整控制参数,这增加了实际应用中的繁琐性。对此,Hu等[15]讨论了复杂网络的预设时间同步,该同步时间作为参数由设计者提前设定在控制协议中,可以根据任务的需求相应调整,具有更好的实用性。
然而,上述文献仅考虑网络节点之间是合作关系。事实上,在实际生活中,网络节点之间不仅存在合作关系,还有可能存在竞争关系,该网络称之为符号网络,其同步称之为二分同步。例如,Mao等[16]讨论了具有不确定参数的CNNs的有限时间二分同步问题。陈苏浩等[17]研究了具有时滞和干扰的CNNs的固定时间二分同步问题。
鉴于以上讨论,本文中主要考虑具有不确定参数与外部干扰的CNNs的固定与预设时间二分同步问题。主要创新点归纳如下:
1) 与文献[15]中无符号图的固定时间完全同步相比,本文中在符号图下研究了固定时间二分同步问题,该网络拓扑中的节点既存在合作关系,又存在竞争关系。
2) 与文献[16]中有限时间二分同步相比,本文中研究了具有不确定参数的CNNs的固定时间二分同步问题,该同步时间与系统初始状态无关。
3) 与文献[17]中固定时间二分同步相比,本文中讨论了具有不确定参数的CNNs的预设时间二分同步,该同步时间可由设计者根据任务需求来提前预先设定。
1 预备知识
1.1 图论
各节点之间的通信拓扑可由无向图G={V,E,A}表示,节点集V={v1,v2,…,vN},边集E⊆V×V,邻接矩阵A=[aij]∈RN×N。对于无向图,如果节点i和节点j之间有边相连,则aij=aji>0;否则aij=aji=0。集合Nj={i:(vi,vj)∈E}表示节点j的所有邻居。
对于符号图G,如果将节点集V划分成2个互不相交的子集V1与V2,且满足∀vi,vj∈Vf(f∈{1,2}),aij≥0;且对∀vi∈Vf,vj∈Vg,(f≠g,f,g∈{1,2}),aij≤0,则符号图G为结构平衡图,反之为结构非平衡图。
1.2 集值李导数
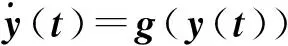

1.3 模型描述
考虑具有N个节点的耦合神经网络(CNNs),其动力学描述为:
(1)

式(1)的同步目标为:

(2)
式中:s(t)=[s1(t),s2(t),…,sn(t)]T表示同步目标轨道。
假设1CNNs的符号图G是连通的且结构平衡的。
引理1[18]若假设1成立,则存在对角矩阵W=diag{w1,w2,…,wN},wi∈{-1,1},∀i∈N,使得WAW=Au为非负矩阵,其中Au=[|aij|]∈RN×N。
假设2CNNs中的激活函数f(x)满足以下条件:
1) ∀x∈Rn,f(-x)=-f(x);
2)f(x)-f(v)≤l(x-v),常数l>0。
假设3不确定参数ΔC(t)和ΔB(t)满足:
ΔC(t)=MG(t)HC, ΔB(t)=MG(t)HB
其中矩阵M,HC,HB是已知的常数矩阵,G(t)是未知矩阵且满足GT(t)G(t)≤In。
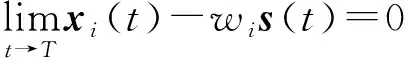
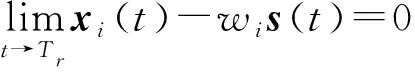
引理2[19]对于任意向量x,y∈Rn和正定矩阵Q∈RN×N,满足2xTy≤xTQx+yTQ-1y。

引理4[15]考虑以下系统:
(3)
式中:y∈Rn,g:Rn→Rn是不连续但局部可测的函数,并且g(0)=0。如果存在连续正定且径向无界函数V(y):Rn→R满足
其中,k∈R,α>0,β>0,ζ>1,0≤ξ<1,则有如下结论:
1) 当k≤0时,式(3)的平衡点是固定时间稳定的,并且驻留时间的上界为:
其中,ε=(1-ξ)/(ζ-ξ)。
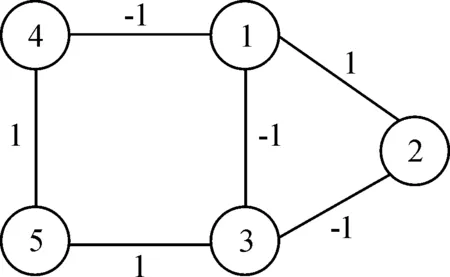
2) 当0 引理5[15]对于式(3),如果存在连续正定且径向无界函数V(y):Rn→R满足 引理6[15]对于式(3),如果存在连续正定且径向无界函数V(y):Rn→R满足 αVζ(y(t))-βVξ(y(t)) 研究结构平衡图下CNNs的固定时间二分同步问题。 (4) (5) 令ei(t)=wixi(t)-s(t),针对式(1),设计控制器如下: ui(t)=-λ1sign(wiei(t))-λ2sigθ(wiei(t)) (6) 其中,λ1>0,λ2>0,θ>1,sigθ(x)=sign(x)|x|θ。 将式(6)代入式(2)和(5),可得误差系统: ei(t)=-(C+ΔC(t))ei(t)+ λ1sign(ei(t))-λ2sigθ(ei(t)) (7) 证明由于式(7)是非连续的,需引入微分包含理论。记式(7)右端为Φi(t),并记Φ(t)=[Φ1(t),Φ2(t),…,ΦN(t)]T,由Filippov集值映射可得: F[Φi(t)]=F[-(C+ΔC(t))ei(t)+ wiδi(t)-λ1sign(ei(t))-λ2sigθ(ei(t))]⊆ λ1sign(ei(t))-λ2sigθ(ei(t)) (8) 基于可测选择理论,选取函数μi(t)∈sign(ei(t))。由式(8)可得: ei(t)=-(C+ΔC(t))ei(t)+ λ1μi(t)-λ2sigθ(ei(t)) (9) 构造Lyapunov函数 并沿着式(9)对V(t)关于时间t求集值李导数,可得: wiδi(t)-λ1μi(t)-λ2sigθ(ei(t))] (10) 基于引理2、假设3,可得: (11) 基于引理2、假设2和3,可得: (12) 因为矩阵Lu是行和为0且半正定的,特征值满足0=λ1(Lu)<λ2(Lu)≤…≤λN(Lu)。可得: (13) 对于有界的外部干扰,可得: (14) 基于引理3,可得: (15) 将式(11)—(15)代入式(10)可得: λV(t)-α(V(t))θ-β (16) 当λ≤0时,式(16)变为: LΦV(t)≤-α(V(t))θ-β (17) 由引理4中结论1)可知,CNNs在固定时间内同步到目标轨道,且同步时间满足: 当0<λ 其中,η=4αβ-λ2。 证明完毕。 注1与文献[16]中研究的具有不确定参数的CNNs的有限时间二分同步不同,本文中研究的是固定时间二分同步,该同步时间与系统的初值无关。 讨论在结构平衡图下,CNNs的预设时间二分同步问题。 首先,对于λ≤0的情形,设计控制器如下: (18) 此时,式(9)为: ei(t)=-(C+ΔC(t))ei(t)+ (19) 证明考虑相同的Lyapunov函数V(t),沿着式(19)对V(t)关于时间t求集值李导数,可得: (20) 与式(14)相似,可得: (21) 进而, (22) 由引理6可知,CNNs在预设时间内同步到目标轨道,同步时间为Tr。证明完毕。 对于0<λ (23) 此时,式(9)为: ei(t)=-(C+ΔC(t))ei(t)+ (24) 证明由式(24)对Lyapunov函数V(t)关于时间t求集值李导数,可得: (25) 进而, (26) (27) 由引理6可知,CNNs在预设时间内同步到目标轨道,同步时间为Tr。证明完毕。 注2 以上同步时间Tr是用户提前预设的,不需要估算,且与控制器和系统参数都无关。 注3二分同步问题在军事、生物以及物理领域中都有许多潜在的应用。例如,无人飞行器在执行侦察任务遇到障碍物时,需要控制所有飞行器向两侧展开以实现避障的目的。 给出2个数值模拟来验证所提控制协议的有效性。 例1在结构平衡图(图1)下,考虑5个节点构成的耦合神经网络(CNNs)的固定时间二分同步问题,其中,节点集V划分为V1={1,2}和V2={3,4,5},则矩阵W=diag{1,1,-1,-1,-1}。目标节点的初值s(0)=[1,-1]T。选取初始状态x1(0)=[0.5,0.8]T,x2(0)=[-0.9,1.6]T,x3(0)=[-2,-3]T,x4(0)=[0.5,-1.2]T,x5(0)=[-0.5,1]T。取CNNs的系数如下: 邻接矩阵: 图1 耦合神经网络(1)的通信拓扑 图2 λ≤0时,CNNs的固定时间二分同步误差 图3 0<λ 当θ=2,η=4αβ-λ2=42.443 7时,由定理1可知,CNNs固定时间内实现二分同步。仿真结果如图4所示,其收敛时间的上界T3=0.729 7。与T3相比,收敛时间T4更精确。 图4 0<λ 例2考虑CNNs在结构平衡图(图1)下的预设时间二分同步问题。令式(18)的参数为λ1=5,λ2=2,θ=1.5,Tr=0.5。由定理2可知,CNNs在预设时间内实现二分同步,其收敛时间的上界Tr=0.5,仿真结果如图5所示。 下面考虑0<λ 图5 λ≤0时,CNNsr的预设时间二分同步误差 图6 0<λ 解决了具有不确定参数和外部干扰的耦合神经网络的固定时间和预设时间二分同步问题。基于Lyapunov稳定性理论和非光滑分析,设计了一类简单的控制协议,确保了耦合神经网络在结构平衡图下实现固定时间和预设时间二分同步。最后,通过2个仿真例子验证了控制协议的有效性。
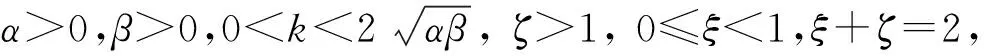
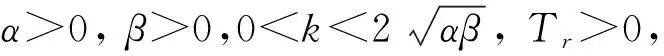
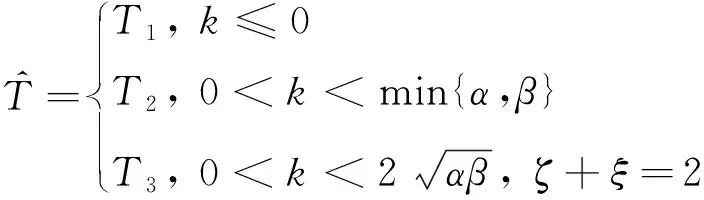
2 主要结论
2.1 结构平衡图下的固定时间二分同步

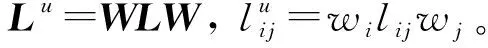



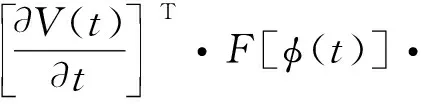



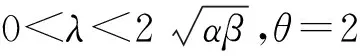
2.2 结构平衡图下的预设时间二分同步
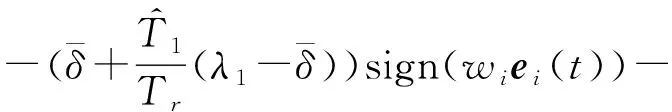




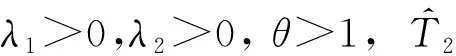
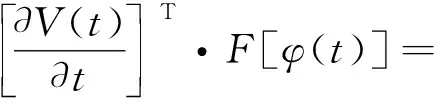

3 数值仿真

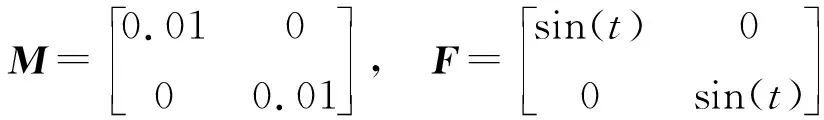

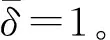





4 结论
