面向决策行为预测的多层策略网络随机游走模型

李晓寒,祁明泽,邓宏钟

(1.国防科技大学 系统工程学院， 长沙 410073； 2.国防科技大学 文理学院， 长沙 410073)

0 引言

决策者只需做出一次决策的决策过程称为单阶段决策过程。在现实世界中，特别是在双方的交互对抗中，人们可能需要对同一决策过程反复决策，这样的决策过程称为多阶段决策。多阶段决策是很多问题的基础，如在博弈对抗时，单方的决策过程可以看作是一个多阶段决策过程[1-2]。很多时序过程，如股票涨跌[3]、天气预测[4]也可以通过对时序数据进行序列分组的方法转换为多阶段决策过程。因此分析多阶段决策问题对解决现实生活中的问题有重要意义。传统的多阶段决策过程常被建模为马尔可夫链，即假设决策人以固定策略转移概率进行依次决策，当前策略仅受上一阶段的决策的影响[5]。但是决策人的决策行为实际上会受到阶段结果的影响，例如本阶段的策略获利后，下一阶段继续采取该策略的可能性会增加，此时，传统的马尔科夫链不再适用。为了解决该问题，探究决策过程中人的决策行为规律，本文中引入了复杂网络中随机游走(random walks,RWs)的方法。

复杂网络的随机游走模型[6]能够刻画决策行为的随机性，游走过程可以描绘决策人的决策过程，进而刻画其行为规律，依据该规律可以对未来决策行为进行预测。网络上随机游走过程的算法及其应用研究受到广泛关注，标准的随机游走过程是指随机游走子按照与边权重成比例的概率移动到另一个邻居。除此之外，人们还提出了其他类型的随机游走，例如相关随机游走、自避免随机游走、乘法随机游走过程和自适应随机游走等[7]。这些不同类型的游走过程广泛应用于不同的场景中，例如，乘法随机游走过程是研究金融市场动态变化的有力工具[8]，自适应随机游走通常会被用于研究生物系统中的动物迁徙过程[9]。此外，随机游走还是很多网络算法的基础，在关键节点、边或者其他关键网络结构的识别过程中[10]，人们通常利用随机游走的轨迹去搜寻重要节点、边或网络结构，例如经典的PageRank算法[11]和特征向量中心性[12]。近年来，在单层网络上的随机游走基础上，人们还研究了时序网络[13-14]和多层网络[15]上的随机游走过程。朱义鑫等[16]提出了时序网络上基于随机游走的免疫策略，解决了传统免疫模型在时序网络中所面临的难以收集拓扑信息的困境。多层网络上的随机游走多被用来研究网络扩散[17]和传播过程[18]，Gómez等[17]通过研究多层网络上的随机游走过程，发现相比单层网络，多层网络的扩散速度更快。然而，利用多层网络随机游走研究决策过程的相关研究较少。本文中对多阶段决策过程进行分析，首先，构建策略网络模型，利用网络上的随机游走过程对多阶段决策过程建模。随后，将考虑决策阶段结果的决策过程构建为多层策略网络。同时，针对单层和多层策略网络模型，提出了利用历史决策信息的单步策略预测算法。最后，为了探寻模型与预测算法的有效性，采用多阶段决策过程仿真数据和典型博弈场景决策数据进行实验验证。

1 基于单层网络的多阶段决策模型

研究的多阶段决策过程是由若干个阶段组成的重复决策过程，即相同结构的决策过程重复多次，其中每次决策称为阶段决策。虽然重复决策过程形式上是原决策过程的重复进行，但是对于决策者来说，并不是简单的重复。决策者会依据上一阶段的策略或结果选择下一阶段的策略。决策过程中出现的所有可能策略的集合组成策略空间。当前阶段到下一阶段采取的策略的变化称为策略转移。假设多阶段决策过程有t个子阶段，则各个子阶段决策过程中依次采取的策略可以组成一个决策序列，称该决策序列为决策链，用(s(1),s(2),…,s(t))表示，其中s(i)(i=1,2,…,t)为决策者在第i个子阶段采取的策略。

1.1 策略网络

策略网络(strategy network)是以策略空间中的策略为节点，策略之间的转移关系为有向边，策略转移概率为边权重构建的有向加权网络。记有限策略空间为S={s1,s2,…,sk}，k为策略空间中策略的数量，则策略网络的邻接矩阵可以表示为：

(1)

式中：wij为节点i与节点j之间有向边的边权重，表示决策过程中当前子阶段采取策略si，下一子阶段采取策略sj的概率，即wij=p(sj|si)。该矩阵需满足式(2)：

(2)

即任意节点的出度之和为1。上述策略网络的网络结构与边权不变，对应策略转移概率不变的决策过程，将其定义为单层策略网络(single-layer strategy network,SSN)。图1为一个单层策略网络的示意图，它描述了一个策略空间为{A,B,C,D,E}的多阶段决策过程，网络中的有向边表示决策者在决策过程中的策略转移的方向，边的权重表示对应的策略转移概率。

假设决策人的决策行为是不固定的，决策人的每一步决策通常具有随机性，因此多阶段决策过程可以看作是一个策略网络上的随机游走过程。假设在网络上有一个随机游走子，该随机游走子随着网络的边以边权表达的概率进行游走，每个子阶段游走一步。随机游走子在2个节点之间经过的概率就是2个策略之间的策略转移概率。随机游走子在网络上的有限随机游走过程可以表示一个有限阶段的多阶段决策过程，游走过的节点组成的序列构成多阶段决策过程的决策链。图1中蓝色虚线表示一个随机游走实例，代表了一个阶段数为4的多阶段决策过程，决策链为(A,C,D,E)。

图1 单层策略网络示意图

1.2 基于单层策略网络的单步预测算法

通常，决策者在决策过程中策略转移的概率是未知的，因此网络的边权重及拓扑结构是未知的，若能根据历史决策阶段的决策策略得到策略转移概率，便可对该决策者未来的决策策略进行预测。针对策略网络为单层网络的决策情形，笔者提出了一种单步策略预测算法。所谓单步预测是指在前t-1阶段的决策策略已知的情形下，预测t阶段最可能的决策策略。采取频率近似概率的思想，利用历史决策信息估计策略网络的拓扑结构和边权重，进而对决策行为进行单步预测。

历史决策信息用决策链(s(1),s(2),…,s(N))表示，s(t)(t=1,2,…,N)表示阶段t采取的策略，算法可预测下一阶段N+1决策者最可能采取的策略s(N+1)，具体算法过程为：

输入：多阶段决策过程前N个阶段的决策链(s(1),s(2),…,s(N))

输出：下一阶段的决策策略s(N+1)

1.初始化任意策略之间的转移频数，即c(sj|si)=0，i,j=1,2,…,k

2.fort=1 toN-1

3.c(s(t+1)|s(t))=c(s(t+1)|s(t))+1

4.end for

6.end for

7.得到下一阶段的策略s(N+1)：

2 基于多层网络的多阶段决策模型

2.1 多层策略网络

上文所描述的模型，决策策略仅受到上一阶段的策略影响，但是决策者在多阶段决策过程中难免会受到决策结果的影响，导致策略转移概率发生改变。例如,在金融市场中，股民会有“追涨杀跌”的决策行为。考虑到阶段结果对决策行为产生的影响，构建了多层策略网络(multiplex strategy network,MSN)。

图2 多层策略网络示意图

2.2 基于多层策略网络的单步预测算法

相较单层策略网络，多层策略网络能够刻画结果对决策行为的影响，能够捕捉决策者在不同阶段结果下的决策行为习惯。对于阶段结果已知的多阶段决策过程，可以利用包含阶段策略和阶段结果的历史决策信息估计多层策略网络的拓扑结构和边权重，进而估计不同阶段结果下策略转移矩阵概率，以预测单步策略。包含阶段结果的历史决策信息用决策链((s(1),r(1)),(s(2),r(2)),…,(s(N),r(N)))表示，其中，s(t)(t=1,2,…,N)表示阶段t采取的策略，r(t)(t=1,2,…,N)表示阶段t产生的阶段结果，利用单步预测算法可预测N+1阶段决策者最可能采取的策略s(N+1)，具体算法预测过程如下：

输入：多阶段决策过程前N个阶段的决策链((s(1),r(1)),(s(2),r(2)),…,(s(N),r(N)))

输出：下一阶段的决策策略s(N+1)

1.令R=∅，m=0，R表示阶段结果集合，m表示集合中元素的个数

2.fort=1 toN-1

3.ifr(t) not inR

4.putr(t) inR

5.m=m+1

6.c(si|sj,r(t))=0,i,j=1,2,…,k

7.c(s(t+1)|s(t),r(t))=c(s(t+1)|s(t),r(t))+1

8. else

9.c(s(t+1)|s(t),r(t))=c(s(t+1)|s(t),r(t))+1

10.end for

15.end for

16.end for

17.得到下一阶段的策略s(N+1)：

3 实验验证

为了验证预测算法的有效性，针对仿真数据和一个重复猜拳博弈数据，设计了单步预测实验。将随机预测(RAND)作为对照组，比较和评估了基于单层策略网络的预测算法(SSN)和基于多层策略网络的预测算法(MSN)的预测效果。

3.1 仿真数据生成

假设一个多阶段决策过程的策略矩阵的拓扑结构及边权重是已知的，则可利用网络上随机游走过程生成仿真决策数据。在实验中，利用图2给出的边权已知的多层策略网络生成了任意阶段数的决策链，从多个方面评估了预测算法的有效性，决策链的生成算法如下：

输入：边权已知的多层策略网络，网络层邻接矩阵的集合为W={W[1],W[2],W[3]}，阶段数N

输出：阶段数为N的决策链((s(1),r(1)),(s(2),r(2)),…,(s(N),r(N)))

1.随机给定初始策略s(1)、阶段结果r(1)

2.fort=1 toN-1

3.在多层策略网络的当前结果层r(t)进行一次随机游走，得到下一阶段的决策策略s(t+1)

4.在阶段结果层之间等概率随机游走，得到下一阶段的结果r(t+1)

5.将当前决策链更新为：{(s(1),r(1)),(s(2),r(2)),…,(s(N),r(N)),(s(N+1),r(N+1))}

6.end for

3.2 仿真过程行为预测

准确率是最普遍的评估指标，因此，首先将准确率作为评估指标，分析不同算法在多阶段决策过程单步预测过程中的表现。准确率可以理解为对于随机一条决策链进行单步预测，预测策略与真实策略相同的概率。在具体实验过程中，通过改变初始策略，利用3.1节提出的算法生成了若干相同长度的决策链，并对每条决策链进行单步预测，对于n条长度相同的决策链，若预测正确的决策链数量为n1，则准确率定义为：

(3)

预测准确率除了会受到算法效果的影响，还会受到生成决策链数量n的影响，因此需要选择合适的参数n。首先固定历史决策阶段数为100，考察不同决策链数量对准确率的影响，结果如图3所示，首先可以初步看出基于多层策略网络的预测算法有较高的预测准确率。此外，还可以看出当决策链数量较少时，准确率会呈现较大的波动幅度。随着决策链数量的增加，预测的准确率趋于平稳，因此决策链数量越多，最后得到的准确率也最可靠。为了衡量随着决策链数量变化，准确率波动幅度的大小，定义了准确率误差：

(4)

式中：A(n)表示决策链数量为n时的预测准确率。为了考察在决策链数量为9 900～10 000准确率误差的变化，绘制了如图4所示的散点图，可以看出，随着决策链数量的变化，误差会上下波动，但波动范围不超过6×10-5。当决策链数量为10 000 时，准确率的误差小于10-4，可忽略不计。因此，设定每次实验生成决策链的数量为10 000。

图3 准确率随决策链数量变化图

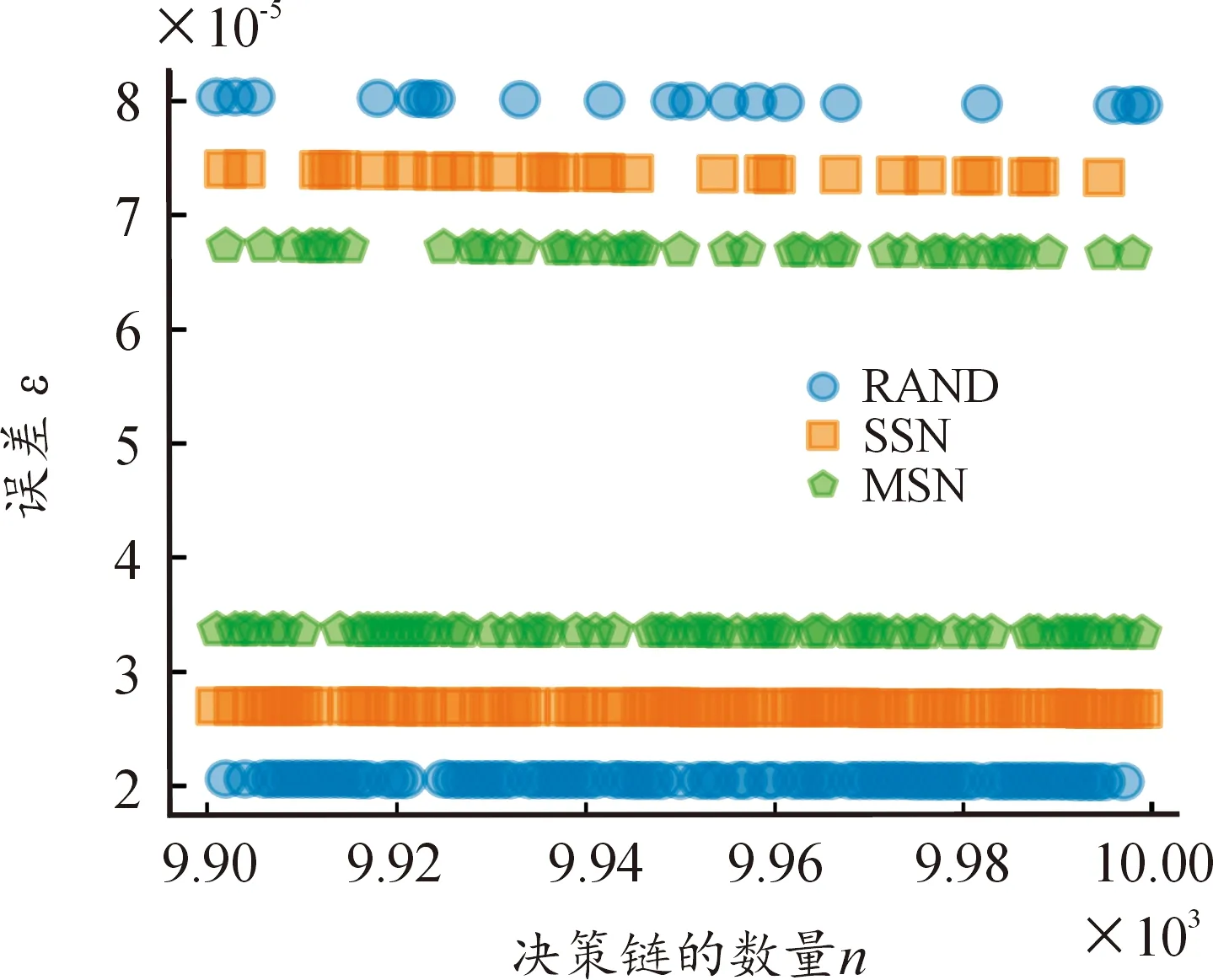
图4 误差随决策链数量变化图

准确率可以从整体上衡量预测的准确性，为了更全面地评估算法效果，还采用了精确率、召回率和F1-score等算法评估指标。精确率和召回率可以从局部衡量预测的准确性，对于每一个策略i，可以定义其预测精确率和召回率分别为：

(5)

(6)

式中：TPi为预测策略为i，真实策略为i的决策链数量；FPi为预测策略为i，真实策略不为i的决策链数量；FNi为预测策略不为i，真实策略为i的决策链数量。对于策略空间中k个策略的预测效果，可以用单个策略指标的平均值来衡量，具体为：

(7)

(8)

F1-score指标为精确率和准确率的调和平均数，定义为：

(9)

图5给出了不同历史决策链长度对预测效果的影响，(a)、(b)、(c)和(d)分别表示固定决策链数量为10 000时，不同算法在准确率、精确率、召回率和F1-score 4种评估指标下的表现。

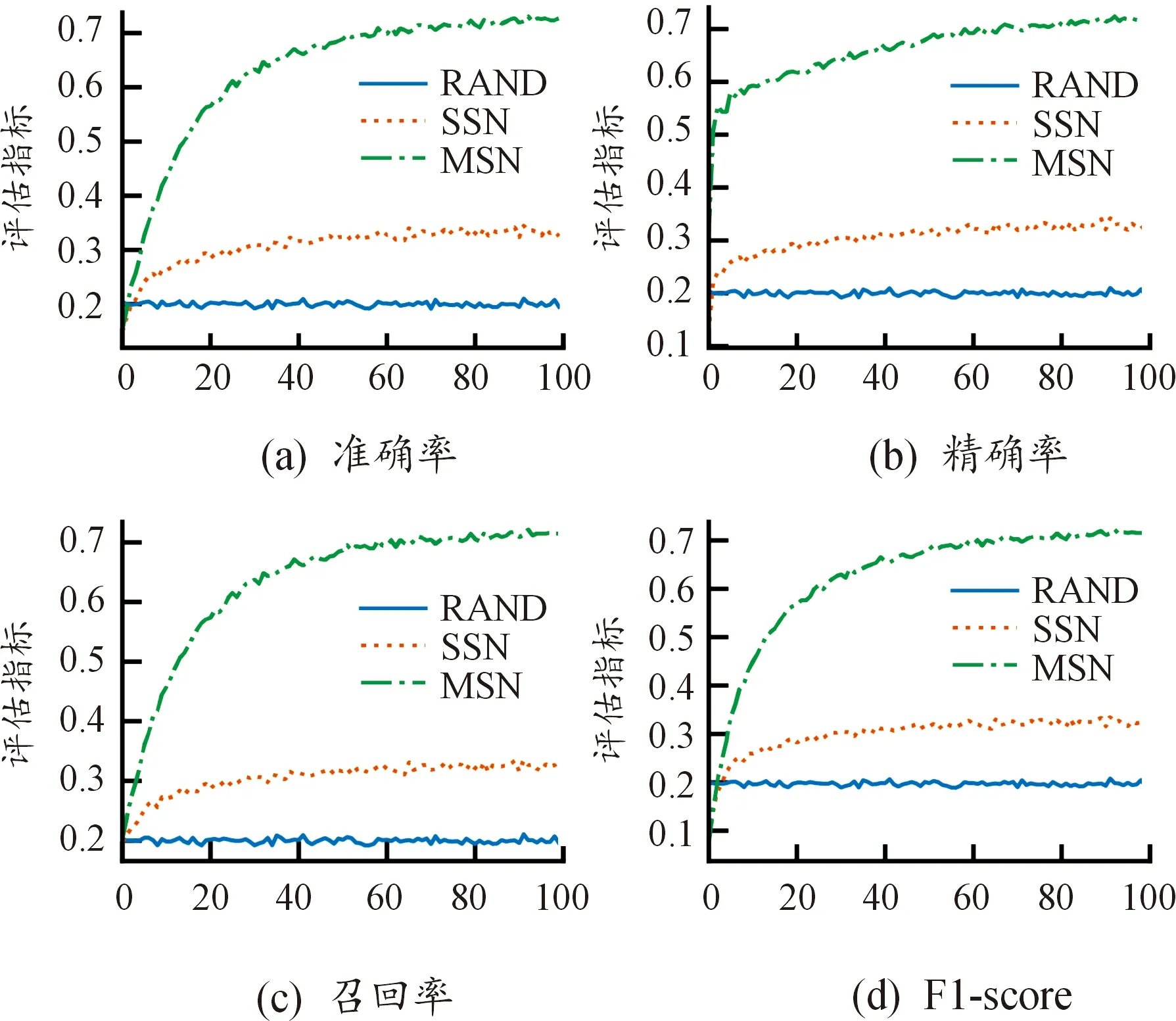
图5 不同评估指标随决策链历史阶段数变化图

从图5(a)可以看出，随机预测的准确率为0.2左右，是策略空间中的策略总数的倒数。基于单层策略网络的预测算法的准确率会随着决策链历史阶段数数量的增加而增加，当决策链历史阶段数增加到30时，准确率趋于平缓，稳定在0.3左右。这说明若当决策链中前30个阶段的决策策略和阶段结果信息已知，利用单层策略网络可以对决策链的下一阶段策略进行预测，但预测准确率仅比随机预测高0.1。基于多层策略网络的预测算法的预测效果要优于其他2种方法，其准确率也会随着决策链阶段数数量的增加而增加，当历史决策阶段数达到60时，准确率平缓，稳定在0.7左右。可以看出基于多层策略网络的预测算法能够得到较好的单步预测准确率，但需要更多的历史决策信息。此外，从图5(b)、(c)和(d)可以看出，对于在精确率、召回率和F1-score评估指标，基于多层策略网络的预测算法的效果仍是最好的。4种评价指标的预测结果相似，因此在后文的实验中，主要用准确率评估算法效果。

3.3 重复猜拳过程行为预测

为了进一步验证提出的模型能够有效捕捉决策人的决策行为习惯，在重复猜拳的决策数据集上进行单步策略预测实验。

首先通过模拟双方的重复猜拳过程得到决策数据，假定一方为随机出招决策人，另一方为具有固定习惯的决策人。考虑了2种常见的猜拳习惯，第1种为“赢存输平变”，即若己方赢了，则下一轮以较大概率继续采取本轮策略；若己方输了或双方平局，则下一轮以较大概率采取能战胜敌方本轮策略的策略。第2种为“赢输变平存”规则，即若己方赢了，则下一轮采取敌方策略，若己方输了，则下一轮采取能战胜敌方本轮策略的策略，若双方平手，则下一轮保持本轮策略不变。利用博弈过程中生成的决策数据，以及多层策略网络对决策过程进行建模，并结合预测算法，可有效地捕捉到决策人的出招习惯。

图6为对于决策习惯为“赢存输平变”的决策者的决策行为预测的结果图，图7为对于出招习惯为“赢输变平存”的决策人的决策行为预测的结果图。在这2个预测中，基于多层策略网络的预测均取得了较好的效果，预测累积准确率均能达到0.8左右。在每次预测过程中，都会估计多层策略网络，图8(a)和(b)分别给出了在历史决策链长度为50和100时多层策略网络邻接矩阵的估计值。

图6 预测准确率随决策链历史阶段数变化图

图7 准确率随决策链历史阶段数变化图

图8 多层策略网络邻接矩阵的估计

该邻接矩阵可以反映出决策人的决策习惯，当决策链长度为50时，多层策略网络邻接矩阵反映的出招习惯还不准确，预测准确率仅能达到0.7左右，当决策链长度为100时，多层策略网络已经能较为准确地反映用户地决策习惯，且预测准确率能达到0.8左右。

4 结论

研究了单层策略网络及网络上的随机游走过程，为多阶段决策过程提供了一种网络模型，同时在此基础上提出了单步策略预测算法。此外，将单层策略网络拓展为多层策略网络，提供了考虑阶段结果的决策过程的网络模型，提出相应预测算法。通过实验发现，考虑基于多层策略网络的预测算法的预测准确率远高于基准水平和基于单层策略网络的预测算法。

本文中定义的决策网络的预测场景可用于运动员行为习惯分析、多智能体系统行为预测和体系对抗博弈等领域，具体应用效果将结合实证数据进一步分析。同时，对于阶段结果如何界定、历史数据如何获取等问题，也有待进一步研究。此外，对于决策过程中，决策空间随时间变化的场景，可以结合时序网络的随机游走过程开展下一步研究。