平面二维时栅位移传感器电气系统设计

钟自强,武 亮，张天恒，童 鹏

(1.重庆理工大学 机械工程学院， 重庆 400054；2.重庆理工大学 机械检测技术与装备教育部工程中心， 重庆 400054)

0 引言

高速高精度测量技术作为现代化信息技术的重要组成部分，已成为现代装备制造行业中的关键和通用技术，在国民经济发展中起着重要的作用。随着科学技术的发展，MEMS系统、微电子制造和平面精确定位反馈系统等众多领域中都需要高精度的平面二维测量。而且随着芯片制造业和高档数控加工中心等高端制造装备的快速发展，高速、高精度的二维平面测量系统成为行业发展的共同需求[1-3]。现阶段二维测量系统主要分为：堆栈式测量系统、二维光栅测量系统、二维电容测量系统、二维电磁测量系统和图像检测测量系统。其中堆栈式结构式在测量平面中安装相互正交的2个一维位移传感器，但是2个传感器的正交性难以保证，易造成阿贝误差。因此不少专家学者提出了大量的二维平面位移测量方法，以避免在测量中引入阿贝误差。

文献[4-9]中提出利用二维光栅衍射规律和二维光栅自准直测量结构，设计了二维光栅测量系统，并通过BP神经网络实现了高倍细分倍数，实现了高精度的二维位移测量。Guo等[10]提出了一种基于频移复用理论的激光外差自混合干涉技术的单点二维位移测量新方法，该方法的二维分辨率均优于5 nm，且标准差优于5 nm。章烨辉[11]设计的大量程平面电容传感器在70 mm×70 mm的满量程内的测量误差为4.5 μm。王合文等[12]设计的离散编码式二维电容位移传感器，在160 mm×160 mm的测量范围内，传感器位移误差峰峰值为13.1 μm和11.8 μm。Wu等[13]提出了一种利用平面线圈在空间中构筑驻波磁场的二维位移传感器，通过CORDIC算法解算出空间位移量。Guelpa等[14]对周期变化的条纹图案进行了二维化设计，并提出了基于相位相关技术的双比例方法，实现了对二自由度的高精度测量，其在 221 μm×221 μm范围内的重复测量精度可达 14 nm，测量分辨率为0.5 nm。

笔者及所在团队在前期的研究中，设计了基于平面线圈的一维磁场式时栅位移传感器，实现了精度为1 μm的位移测量，并在此基础上设计了基于正交双行波磁场的二维磁场式时栅位移传感器[15]。但是在前期的验证实验中，仍然沿用了一维时栅位移传感器的电气系统。该测量系统的解算主板和信号处理板分离，且只能采集单路信号，在实验室需借助两套电气系统，无法满足同时处理两路信号的要求，且极易受到外部差模信号的干扰，造成信号失真，在测量结果中引入大量的二次谐波误差。由于两路感应信号独立处理，极易造成差模干扰，也会影响传感器的测量精度。

基于上述问题，提出一种适用于平面二维时栅位移传感器的电气系统。该电气系统实现两路传感器感应信号在一个主板中进行解算，实现了同时处理，并且根据二次谐波误差的来源，采用减法器和滑动变阻器调整激励信号的相位和幅值，大幅度降低二次谐波误差。通过实验验证了该电气系统的可行性，提高了传感器的测量精度。

1 测量原理

磁场式时栅的核心是构建匀速运动磁场，利用磁场作为时域信息和空域信息的载体，通过电磁转换，产生一个关于时间域和空间域的电行波信号。该电行波信号e(t,x)可以表示为:

(1)

式中：A为时域函数幅值；B为空域函数幅值；T为时域函数周期；W为空域函数周期；t为时间；x为位移。将式(1)通过三角恒等变换就可以转化为2个拍频驻波相加的形式：

(2)

由式(2)可以看出，行波信号是由2个空间驻波信号叠加而成，而空间驻波信号是在激励线圈中的正弦绕组和余弦绕组中通入激励信号sinωt和 cosωt，线圈中各个导线段产生的磁场强度在空间中的叠加。如图1所示，假设在空间中的平面闭合线圈ABCD中通入大小为Im的电流，根据毕奥-萨法尔定律可以得出在空间中一点P(x,y,z)的磁场强度为导线AB,BC,CD,DA分别在P点产生的磁场强度的垂直分量的叠加，由P点的磁场强度可分别进行计算并进行叠加，且l=Ltanθ和 |QP|=L/sinθ。选取AD段中的电流元dl，则AD段在P点产生的磁场强度就等于dl沿AD段上积分的结果，其磁场强度大小为：

(3)

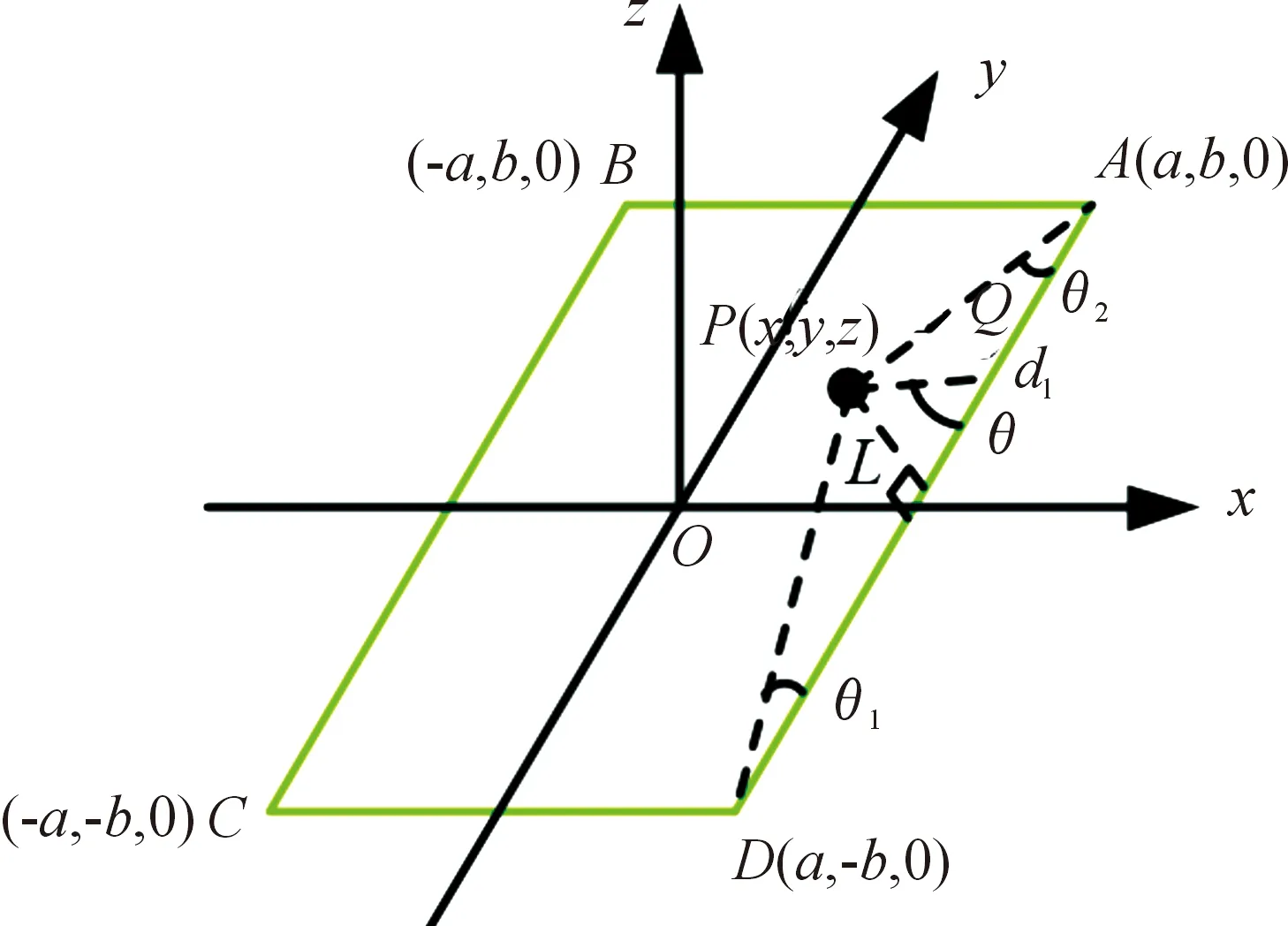
图1 传感器激励线圈计算模型

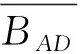
(4)

式中：d为点P(x,y,z)在平面XOY中的投影到导线AD的距离，同理，其余3根导线在P点的磁场强度与导线AD类似，故平面闭合线圈ABCD所产生的磁场强度点P(x,y,z)的大小就为4条导线段所产生的磁场强度的Z轴方向上的分量的叠加。

当感应线圈在激励线圈上方沿x方向移动时，通过感应线圈的磁通量以W为截距呈现周期性变化，满足狄利霍利条件，因此可以通过傅里叶级数展开，如式(5)所示。

(5)

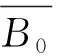
(6)

(7)

在只考虑基波磁场产生的磁场强度时，当激励线圈中分别通入i=sinωt和i=cosωt的激励信号时，与线圈中基波产生磁场进行调制，便可获得一个拍频驻波信号，当相邻的2个正弦激励线圈和余弦激励线圈分别产生的拍频驻波信号相互叠加后，在空间中就可以获得一个行波信号：

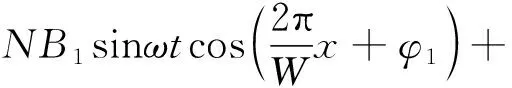
(8)

式中：B1为基波幅值，借鉴一维时空坐标转换原理，将2个一维传感器在平面空间中正交放置在二维平面中，空间位置信息x、y和时间信息t之间分别耦合，从而形成一个包含了时间量t，空间量x，y和磁场强度B的平面空间坐标系。

当x方向上的每组感应线圈覆盖x方向上的激励线圈W/2，覆盖y方向上的激励线圈W时，在只考虑基波的情况下其线圈覆盖的磁场强度为：

(9)

因此，由x方向的激励线圈产生的磁场强度通过感应线圈的磁通量就分为通过x方向的感应线圈和通过y方向感应线圈的磁通量，分别为：

(10)

(11)

同理可得，此时y方向上的激励线圈产生的磁场强度通过x方向上的感应线圈和通过y方向感应线圈的磁通量产生形式与x方向上的感应线圈相同。这样就可以将空间磁场中包含x方向和y方向的空间信息量分离，实现了位移的解耦。当2个感应线圈中的磁通量与激励信号调制叠加合成行波后，再对时间量t求导数便可以得到2个关于位移量x与时间量t，位移量y与时间量t的感应电动势，从而实现了磁场信号的解耦并完成磁电信号的转换。两路电动势表达式如下：

(12)

(13)

根据“时空坐标转化思想”，所产生的匀速坐标系在时间上以T为周期的正弦信号Sr为:

(14)

式中：V为匀速坐标系的运动速度；W为空间周期，并将标准信号转化为方波信号。当电行波信号的行进速度V=Wω/2π时，利用MCU产生的高频脉冲，将两路电行波信号与式(18)的标准信号的上升沿或下降沿的相位差进行插补，进而可以得出其时间之差Δt，从而得出x方向和y方向的位移值。

(15)

(16)

传感器结构如图2所示，传感器包含激励线圈和感应线圈。激励线圈由沿x方向和y方向排列的两层结构参数完全相同的平面线圈线阵组成。x方向平面线圈线阵包括由2组螺旋线圈线阵(Ex_S)和(Ex_C)交替排列，y方向平面线圈线阵同样由2组螺旋线圈线阵(Ey_S和Ey_C)交替排列组成。2组螺旋线圈线阵起始线圈的中心沿排列方向间隔1/4个空间节距(W)。每组螺旋线圈线阵中相邻的2个螺旋线圈串联且绕向相反。

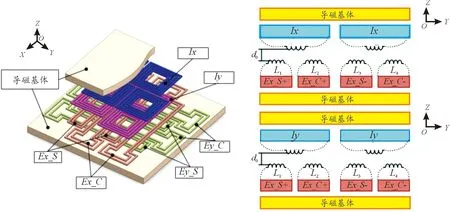
图2 传感器结构图

感应线圈同样为上下两层结构，其中Ix表示用来接收x方向上激励线圈产生的电磁信号；Iy表示用来接收y方向上激励线圈产生的电磁信号。且x方向上的激励线圈和感应线圈之间的间隙(d0)和y方向上的间隙一致，以保证感应信号相同。以感应线圈的x方向感应层为例，由2组相同线圈阵组成，最外层线圈的长度和宽度为W/2。感应线圈分为上下两行，两行之间的中心距为W/6；y方向上的布置方式与x方向相同，并且在感应线圈中x和y方向的线圈之间间隙与激励线圈的间隙相同。

2 传感器电气系统设计

2.1 电气误差分析

根据测量原理可知，传感器激励线圈需要施加两路正交的关于时间量的激励信号与空间量进行调制。然而由于传感器线圈自身的感抗不同，导致激励信号幅值不相等；同时由于原始激励信号比较微弱，需要通过运算放大器对其进行放大处理，但由于运放内部结构左右不对称的特性，因此放大后的信号相位会出现一定的偏差，从而导致两路激励信号不正交，也会导致测量误差。接下来对这2种情况进行具体分析。

2.1.1激励信号幅值不相等

当激励线圈中激励信号幅值不相等时，合成的电行波信号如式(17)所示。

(17)

式中：λ1和λ2表示两路拍频驻波的幅值。根据三角函数中的辅助角公式，可将式(17)转化为式(18)。

(18)

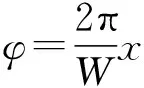
(19)

可以明显看出，误差中包含了一个二次谐波成分。

2.1.2激励信号相位非正交

当激励信号的相位角非正交时，会引入一个偏移角度φ，此时电行波信号表示如式(20)所示。

(20)

式中：λ表示两路拍频驻波的幅值，同样根据辅助角公式，将式(20)转化为式(21)。

(21)

同样提取其中的相位，求出理论位移误差值。

(22)

通过式(22)可以看出，当激励信号的相位非正交时，在误差中会引入一个二次谐波成分和直流偏置。利用Matlab对式(19)和式(22)进行绘图分析，设置幅值偏差比例为1%，相位偏角1°，如图3所示。从图中可以看出，仅仅存在1%的幅值误差和1°的相位偏差都可以引起10 μm左右的位移误差，因此电气系统设计直接影响了传感器的性能。

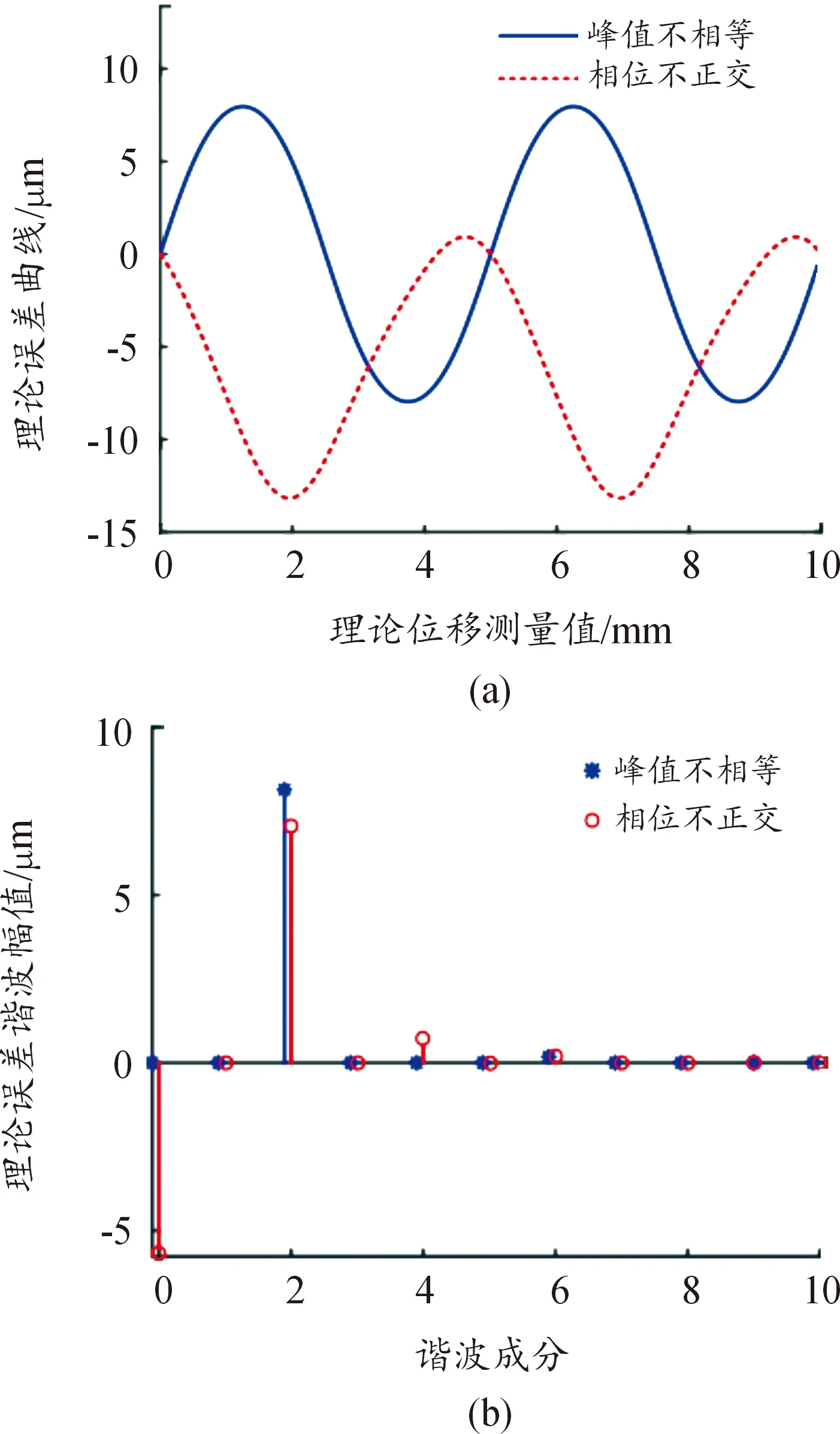
图3 理论误差分析

2.2 电气系统设计

针对以上对电气误差的分析，并结合二维位移同时解算的需要，设计了用于基于平面二维时栅位移传感器的电气系统。本节中重点对激励信号发生模块、感应信号处理模块和位移解算模块进行介绍。

电气系统的主控芯片采用STM32F4系列，为整个电气系统提供DA、TIM计数器和通信等功能。同时位移解算功能也集成在最小系统中，最后将解算结果通过串口发送到上位机中。MCU的最小系统如图4所示。外部晶振使用了24 MHz的无源晶振，通过调整MCU中PLL锁相环中的分频和倍频系数，使整个系统得到150 MHz的基准时钟频率。

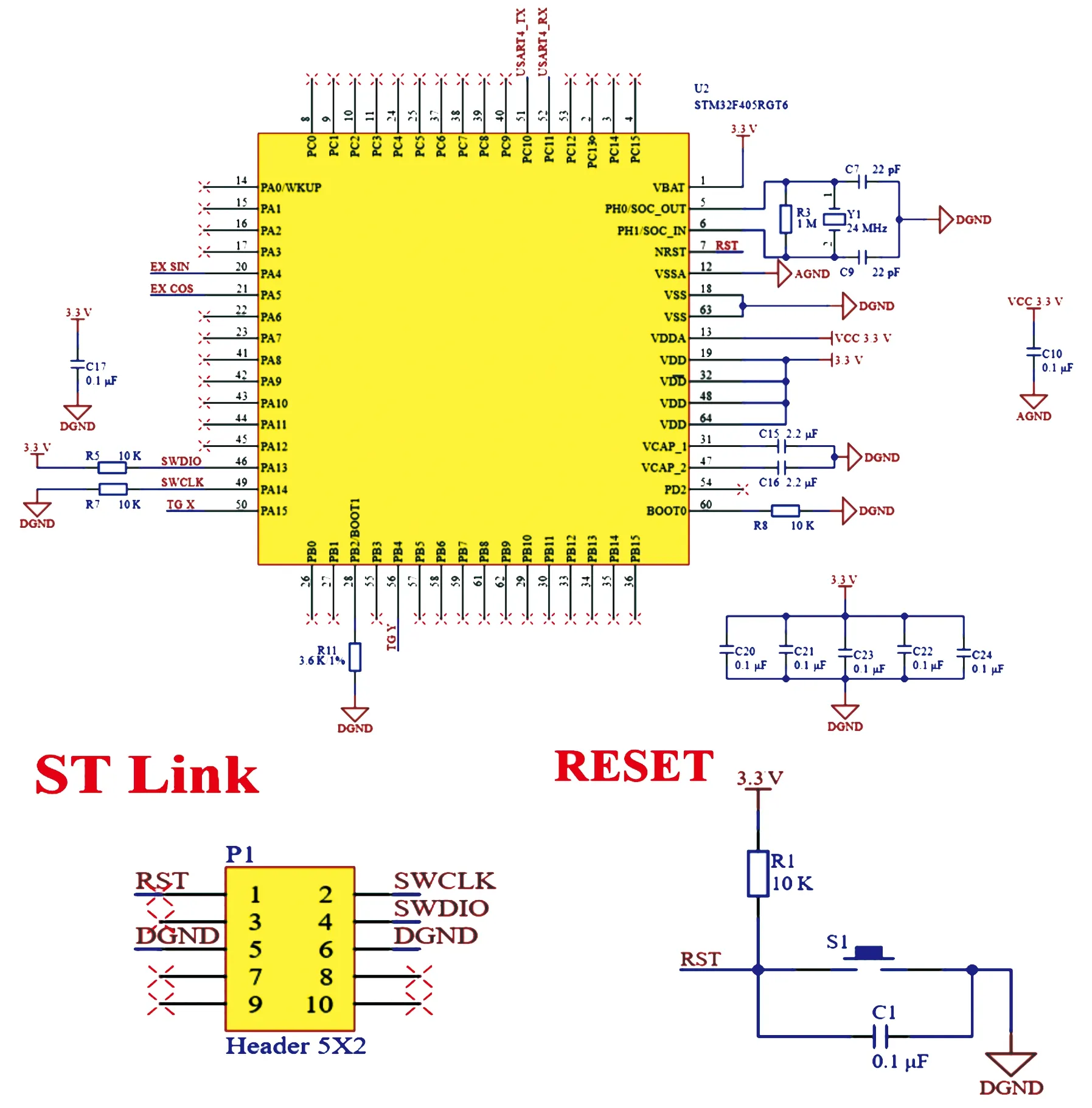
图4 最小系统

正交激励信号利用STM32F4系列芯片中自带的12位D/A功能产生，基准参考电压(VR)选择ADI公司的AD440BRZ基准电压芯片，可为DA稳定提供2.048 V的基准电压。由于采用基准电压芯片输出的模拟信号的电压幅值Vout为0～3.3 V，且为单极性电压源信号，而实际需要的正交激励信号为双极性，因此需要通过精密运算放大器OPA2277搭建减法比例运算电路，将MCU的激励信号输出端和OPA2277的同向端相连，将基准电压芯片ADR440BRZ的基准电压的输出端与反向端相连，如图5搭建减法电路且R33、R36、R39的阻值相同，因此通过减法器后的输出电压V1可由式(23)表示。通过计算可得输出电压为0～2.048 V，实现了电平偏移和双极性电压信号转换。最后通过AD8397对信号功率进行放大，实现激励信号的输出。

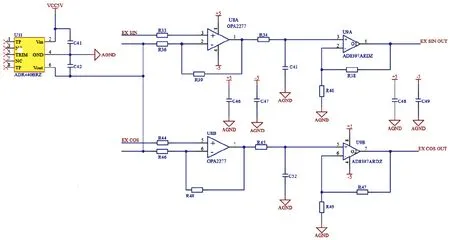
图5 激励信号发生电路

(23)

利用Multisim进行仿真，在交流耦合条件下仿真结果如图6所示，最后输出的信号满足传感器使用要求，为两路正交的交变信号。

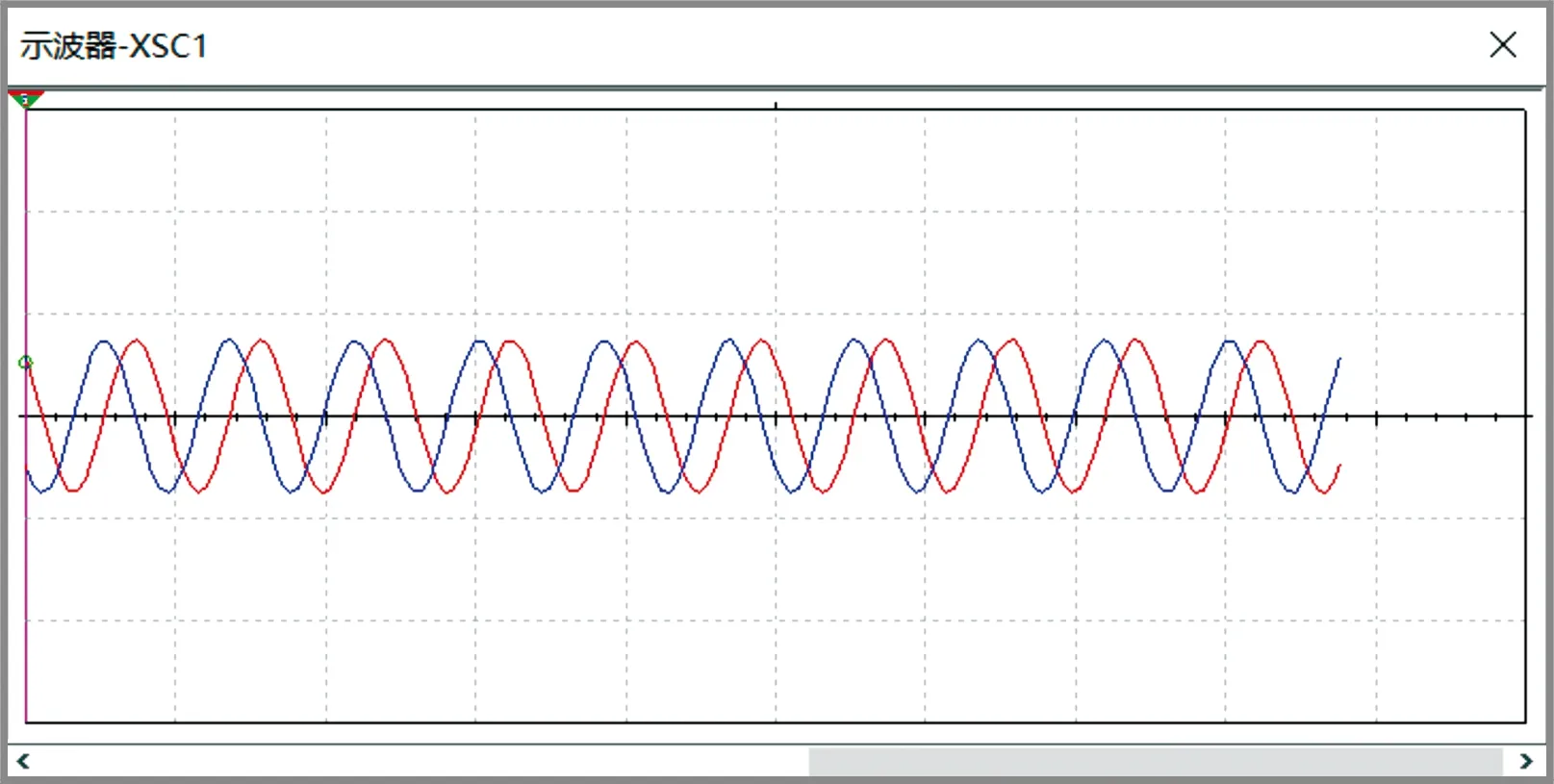
图6 激励信号Multisim仿真结果曲线

感应信号采集电路分为x方向信号采集和y方向信号采集2个部分，根据传感器测量原理可知，感应线圈通过电磁感应原理在线圈中产生电行波信号。但是线圈中的原始信号幅值非常微弱，且信号中混杂有高频谐波成分和工频信号干扰，因此在位移解算之前，需要对信号进行滤波、放大、整形处理，信号处理过程如图7所示。

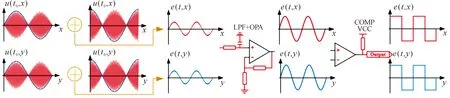
图7 感应信号处理过程

感应线圈中的原始感应信号为共模信号，因此在滤波放大电路设计中优先考虑典型的传感器仪用放大电路，仪用电路具有高共模抑制比、高输入阻抗、低噪声、低温漂的优势。

由于x方向和y方向上的硬件电路相同，因此以x方向的硬件电路为例进行说明，感应信号采集电路如图8所示。在感应信号通过信号线上串联1个阻值较小的电阻R12、R24时，由于并联了1个阻值远大于信号线上的电阻R15和R22，当输入的共模信号分别为Vx+和Vx-，那么信号通过电阻R12后，幅值大小可通过式(24)计算得出Vxout+和Vxout-。这样设计的目的是实现电压跟随，滤除低频成分使电压信号更加稳定。

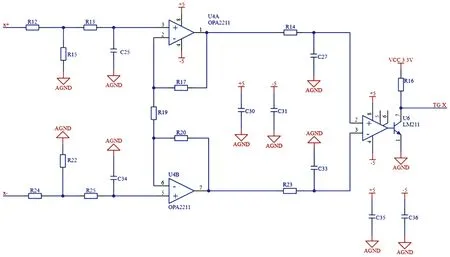
图8 感应信号采集电路

(24)

信号通过分压处理后再通过一个一阶低通滤波器，低通滤波器的RC参数设置和激励信号发生电路中参数一致。然后通过由OPA2211组成的比例放大器。方波整形选用LM211比较器，最后通过上拉电阻将高电平拉高到3.3 V，最后输入到MCU中。感应信号仿真结果如图9所示，从图中可以看出，原始正弦感应信号通过电路滤波、放大和整形后转化为方波信号，且方波信号的高电平为3.3 V，与设想一致。

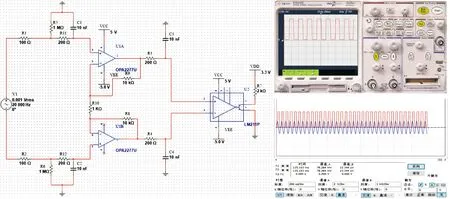
图9 感应信号采集电路Multisim仿真结果

PCB实物图如图10所示。通过对电气系统的设计整合了之前相互独立的信号处理模块和信号解算模块，高集成度的设计进一步缩小了PCB的尺寸，使其元件更加紧凑。通过单点接地的方式消除了电路板中存在的差模信号干扰，进而降低电气系统代入的误差。

图10 电气系统PCB实物图

3 实验研究和结论

用于验证基于平面二维时栅电气系统的实验平台如图11所示。二维移动平台为XYEW-CRG-170二维电动滑台，并且在平台两侧粘贴雷尼绍RH100X30D05A直线光栅带，用于运动反馈和测量，其分辨力为是1 μm，满足当前实验要求。首先测试电气系统的各个信号，包括所需要产生的双路正交的激励信号和通过整形后的两路正交的方波信号。信号测试结果如图12所示。

图11 实验平台

图12 信号测试结果

信号测试结果与Multisim仿真结果一致，证明电路可行。激励信号的幅值通过修改MCU中DA的正弦表实现，并通过高精度的运算放大器和RC移向电路中的阻容值来控制相位的变化。通过比较现有时栅电气系统和本文中提出的电气系统对传感器测量精度的影响，验证误差分析和电气系统的正确性和可行性。

实验过程中，串口可以在115 200的波特率下发送数据且不丢失。在数据位为10位的情况下，8.6 μs发送一个数据，实现了高速采样。使传感器感应线圈沿y=x方向运动一个空间截距，并通过傅里叶分解获得其误差频次。精度实验结果如图13所示。传感器可以有效分辨出5 μm的变化量，且在滑动滤波算法加持下，传感器的分辨率可达到0.2 μm。实验结果同时表明该电气系统有效减小了传感器的二次误差，从之前的40 μm减小到16 μm，但由于PCB在加工和制作中，自身有一定的制造误差，导致PCB中自身的直流阻抗和寄生电容等不相同，使信号的幅值和相位无法做到理论上的相等和正交，因此存在一定的二次误差残留。

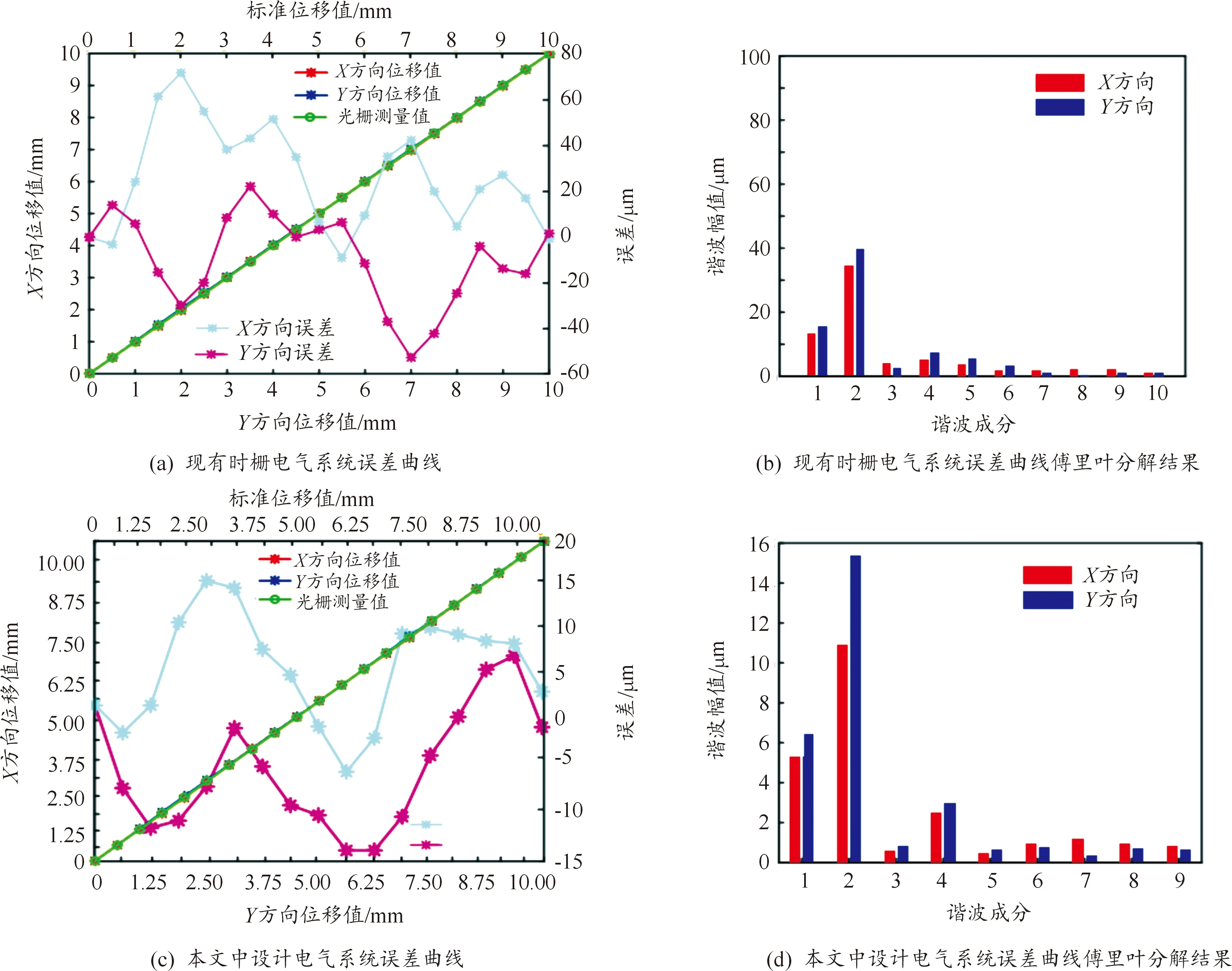
图13 精度实验结果

4 结论

设计了一种用于平面二维时栅位移传感器的电气系统。该电气系统以一维时栅位移传感器的电气系统为基础，将2个独立电气系统功能集成在一块PCB中，并通过对传感器二次误差的分析，设计了激励信号幅值和相位调整电路。通过Multisim仿真和实验验证了电气系统的可行性，实现了两路感应信号同时采样和同时解算的功能。利用地线屏蔽和滑动滤波的方式降低了外界高频杂波的干扰，提高了传感器的分辨力，实现高速实时采样。实验结果表明，使用该电气系统可将传感器二次谐波误差由40 μm减小到16 μm，为制作高精度的平面二维时栅位移传感器提供参考。