机械或液压触发无限级分段压裂滑套研制

付 强，董社霞，李英松，李 越，程文佳

(中海油田服务股份有限公司，天津 300459)

水平井分段压裂技术是伴随着页岩气、致密气、致密油等非常规油气开发而发展起来的一项工程技术[1-2]。目前最常用的技术是裸眼水平井封隔器+滑套技术，其通过投入不同直径的球来打开压裂滑套，实施压裂作业[3-4]。目前的分段压裂技术存在不足：

1) 需要投入不同直径的球与球座配合，实现滑套开启，分段级数有限。

2) 管柱无法实现全通径，增大了压裂液在管柱中流动时产生的摩阻。

3) 后续修井施工时需要钻除滑套的球座，施工复杂，增加了危险性[5-6]。

为了克服现有压裂技术的不足，研制了一种机械或液压触发无限级分段压裂滑套。通过对现有的滑套结构进行改进，实现管柱全通径，降低压裂液在管柱中流动时产生的摩阻，并且提供后期修井作业的无障碍通道。相同尺寸的压裂球可开启全部滑套，避免分段数量受球径的级差限制[7-8]。

1 技术方案分析

本技术的核心是对压裂井内的滑套结构进行改进，通过设计可缩放的弹性套、可变形的可变径球座，以及改进弹性套和可变径球座周围零件结构，从而实现采用同一尺寸的低密度压裂球开启若干级滑套，按指定顺序进行压裂，压裂完成后呈现全通径状态。该技术使得压裂段数无限增加，实现储层的精细化改造。

1.1 弹性套

弹性套结构如图1所示。弹性套结构的创新在于巧妙的解决了全通径滑套的技术难点，即，既要使球能通过，又能为后面的投球做准备。弹性套连续相对的凸块与滑套管壁内的凹槽[9]相对应，在未打开滑套时，始终呈现一端凸块收缩，而另一端凸块弹开进入凹槽的状态。这样的结构，当球过来时，始终有一端凸块能接住球，在液体冲击下，推动弹性套移动，从而使一端凸块弹开，而另一端凸块再收缩。然后重复动作，使压裂球通过的同时，弹性套也按既定顺序被激发，移动规定的距离，直到把需要压裂的的层位所对应的滑套顶开，从而开始压裂作业。此时，弹性套的两端凸块也同时落在了管壁凹槽内，处于弹开状态，并呈无缩径状态。

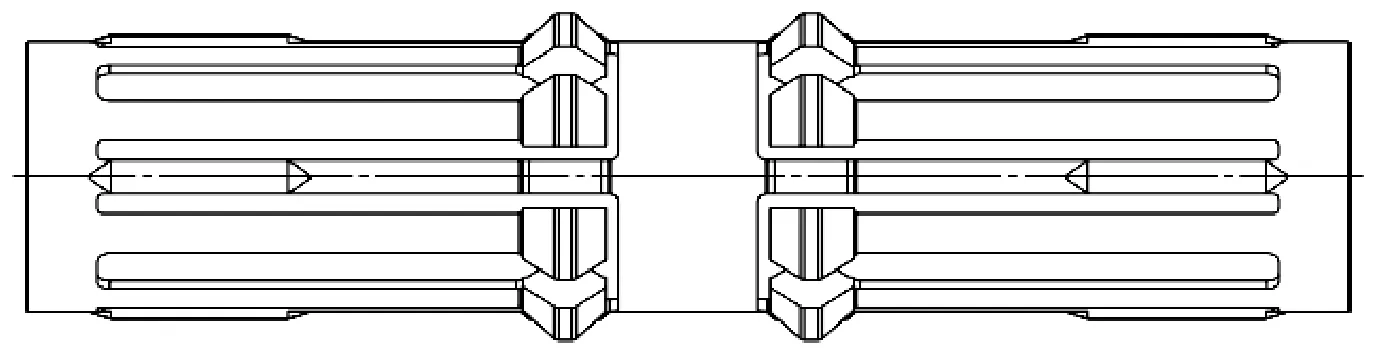
图1 弹性套结构

1.2 可变径球座

可变径球座外形如图2所示。球座的创新在于实现了压裂后球座能变径缩回凹槽，从而实现全通径要求。当内滑套被顶开的同时，此球座也被内滑套推动，使球座的变径爪收缩至管壁内，形成球座，从而能接住压裂球，实现压裂作业。当压裂结束后返排时，球座在弹簧的作用下被推回，弹性爪缩回管壁凹槽，从而实现全通径。

图2 可变径球座外形

1.3 全通径分段压裂滑套

全通径分段压裂滑套的外部由上接头、压裂球、弹性套等组成，如图3所示。在压裂施工中，全通径滑套的内部零件是一个连续的动作过程，在设计中充分考虑了内部各种零件的工作状态，和相互之间的运动关系。

1-上接头；2-压裂球；3-弹性套；4-内滑套；5-密封圈；6-锁块；7-外壳；8-可变径球座；9-复位弹簧；10-球座滑套；11-塞环；12-外套；13-下接头。图3 全通径分段压裂滑套。

以2级滑套为例，对滑套的动作全过程进行图例说明，如图4a所示，第1个球在弹性套上部，弹性套上部弹爪收缩，下部弹爪打开；如图4b所示，第1个球在弹性套中部，弹性套上部弹爪打开，下部弹爪收缩；如图4c所示，第1个球过弹性套后，到达下级滑套，弹性套上部弹爪收缩，下部弹爪打开；如图4d所示，第2个球在弹性套上部，弹性套上部弹爪收缩，下部弹爪打开；如图4e所示，第2个球在弹性套中部，弹性套上部弹爪打开，下部弹爪收缩，内部滑套被推动；如图4f所示，第2个球过了弹性套，弹性套上部和下部的弹爪全部打开，实现弹性套位置全通径，内部滑套内孔和外套的内孔相对，实现油管内部和环空贯通，内部滑套推动下部可变径球座变形收缩成1个闭合的球座；如图4g所示，受压力影响，球推动可变径球座持续向下移动，塞环打开卡住球座滑套；如图4h所示，球被返排液推到上层，受弹簧作用，可变径球座被向上推动，弹开到自由状态，实现滑套内部全通径。

图4 两级滑套在压裂过程中的动作示意

2 力学分析与有限元模拟分析

2.1 弹爪变形与受力分析

压裂滑套内部结构中有两个零件具有弹爪结构，分别是可变径球座和弹性套。

1) 可变径球座弹爪变形分析。

可变径球座的结构及相关尺寸如图5所示。

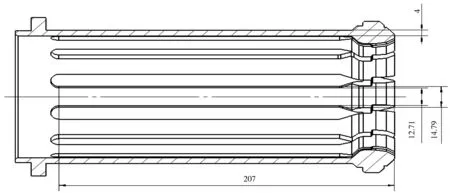
图5 可变径球座结构

弹臂变形如图6所示。根据《机械设计手册》第三卷第十二篇第十章片弹簧中的表12-10-3计算弹臂的工作变形量[10]。设计中，由于外形尺寸限制，可变径球座弹臂的变形量为δ=8 mm。

图6 弹臂变形示意

弹臂的最大变形计算公式为：

式中：δmax为弹臂的最大变形；E为材料的弹性模量；h为弹臂的厚度；b为弹臂的宽度；L为弹臂的长度；σP为材料的许用应力；Fmax为最大径向载荷；J为截面惯性矩。

弹性爪的材料为65Mn硅锰钢，根据《机械设计手册》，取E=205 800 MPa，σP=637 MPa。由图5得，弹臂的厚度h=4 mm，弹臂的长度L=207 mm。

计算得

上述计算的弹臂最大变形量为δmax=22.1 mm，大于设计值δ=8 mm。因此，可变径球座收缩变形后会弹开到自由状态，此处变形设计为可靠设计。

2) 可变径球座回退力计算。

计算可变径球座变形后从球座滑套回退时所需要的力。首先计算出单个弹臂对球座滑套的径向工作载荷，然后再乘以弹臂的数量和摩擦因数，便可以得出可变径球座回退轴向力(也就是复位弹簧的工作弹力)。

根据《机械设计手册》第三卷第十二篇第十章片弹簧中的表12-10-3计算弹臂的最大工作载荷[10]。根据其变形量，求出单个弹臂的工作载荷。

式中：Fmax为弹臂在最大工作极限时的载荷；W为截面断面系数；b为弹臂的宽度，由图5知b=(12.71+14.79)÷2=13.75 mm。

计算得

弹臂对球座滑套内壁的压力为：

式中：F为弹臂触头对球座滑套内壁的压力。

可变径球座共有12个弹臂，以上计算的为单个弹臂对球座滑套内壁的压力，全部弹臂与球座滑套内壁摩擦力计算公式为：

f=12μF

式中：μ为摩擦因数，取μ=0.15。

计算得：

f=12μF=12×0.15×40.84=73.5 N

所以，可变径球座在球座滑套中被拉出时所需要的力为73.5 N。

3) 弹性套受力分析。

结合图7对弹性套进行受力分析。弹性套在壳体内由左向右运动，左边弹爪受到压缩，对内壁产生1个向外的弹力。弹性套向右移动时要克服上接头内壁对左侧弹爪的摩擦力，以及沟槽对右侧弹爪的阻力。

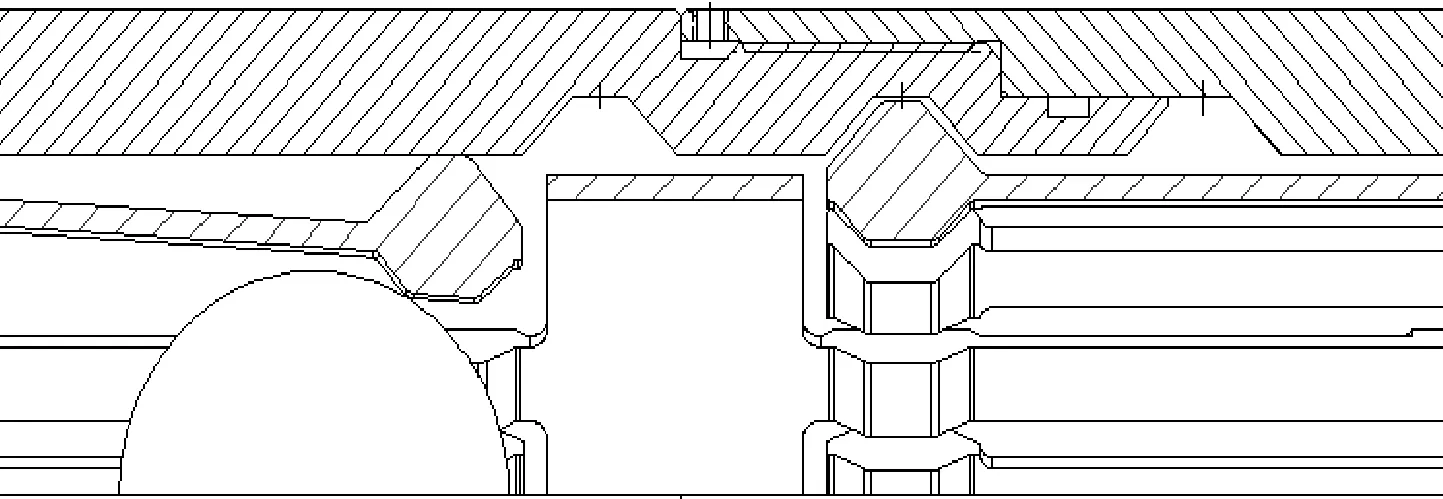
图7 弹性套动作结构

计算左侧弹臂的最大工作极限载荷：

式中：Fmax1为左侧弹臂最大工作极限载荷；b1为弹臂宽度，且b1=13.835 mm；h1为弹臂厚度，且h1=4 mm；L1为弹臂长度，且L1=161.5 mm。

计算左侧弹臂的最大变形量：

弹性套左侧的弹臂实际变形量δ1=8 mm，则计算单个弹臂对上接头内壁的弹力为：

弹性套左侧弹臂共有8瓣，计算左侧弹臂摩擦力为：

f1=8μF1=8×0.15×86.5=103.8 N

则，为克服左侧弹臂摩擦力所需推力为：

Fl=f1=103.8 N

下面计算右侧单个弹臂从沟槽中拉出来所需要的推力Fr。

根据右侧弹臂向右运动的过程画出受力分析图，如图8所示。

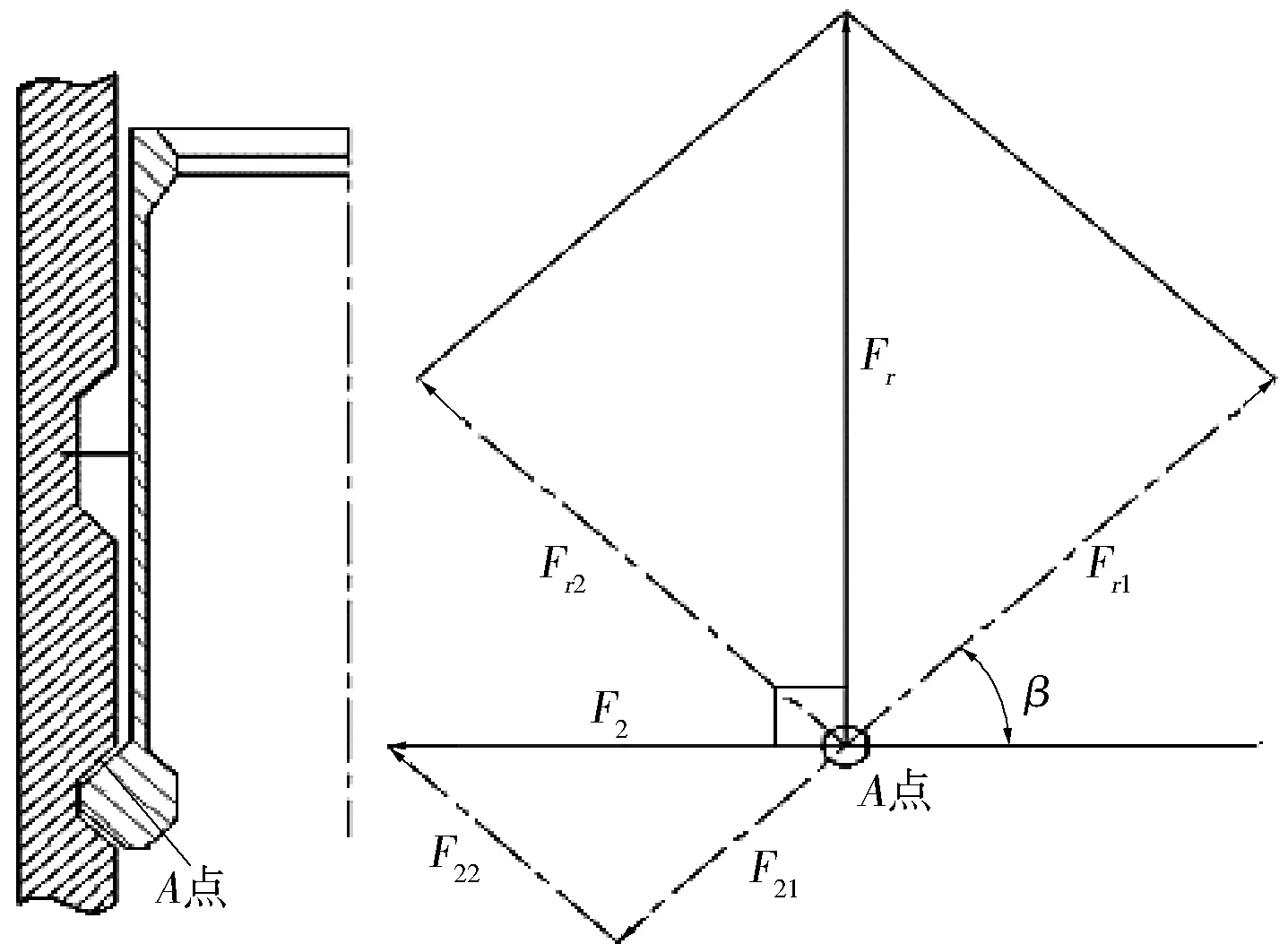
图8 弹臂运动过程受力分析

右侧弹臂移动到上接头内壁所受的力F2和左侧弹臂弹力一致，即F2=F1=86.5 N。

要使弹臂触头能够从沟槽内被拉出，拉力Fr1要克服Fr2和F22对A点产生的摩擦力和F21的合力。列出力的平衡方程：

μ(Fr2+F22)+F21=Fr1

其中：

F21=F2×cosβ
F22=F2×sinβ
Fr2=Fr×cosβ
Fr1=Fr×sinβ

式中：β为沟槽斜面角度，β取45°。

带入已知量，求得Fr=117 N。

根据以上，计算弹性套从左向右移动所需要的力为：

F3=Fl+8Fr=103.8+8×117=1 039.8 N

4) 弹性套应力有限元分析。

建立弹性套的有限元模型，分析得到应力云图，如图9所示。弹性套从凹槽收缩回原位置时只受到弹性套自身的回复力，不会超出屈服极限。因此，只分析从原位置到凹槽的过程中所受到的最大应力值。由图9知，上接头和弹性套的应力均远小于材料的屈服应力，即，弹性套在这个运动过程中应力是在安全范围内。

图9 弹性套的有限元应力云图

2.2 弹性套移动所需流量计算

由于节流产生压降的影响因素十分复杂，目前还没有标准的节流压降的计算方法。所以，在求解之前，进行如下假设[11]：

1) 模型中压裂球以及弹性爪在没有移动时为刚体。当两边压差达到一定值后，压裂球立即脱离弹性爪，脱离时间极小。

2) 外壳内流量变化可看做准稳态过程，即流量随时间的变化梯度为一极小值。

3) 压裂球与弹性爪接触面之前外壳内流体压力均相等，接触面之后外壳内流体压力均相等。

4) 忽略重力作用。

将弹性套结构简化，建立模型如图10所示。压裂球与弹性爪接触面之前外壳内流体压力为p1，流量为Q1，接触面之后外壳内流体压力为p2，流量为Q2。

图10 弹性套的模型简化

根据2.1节计算结果，当推力F3=1 039.8 N时，弹性套可移动。物体所受压力的等效面积等于物体在垂直压力面的投影面积。由图10知，受力面积SP为总面积减去过流面积的差值，即

SP=S-Sg

式中：S为上接头过流面积，S=8 167.14 mm2；Sg为弹性爪闭合状态下客观存在的过流通道等效面积，在三维建模软件SolidWorks中，通过做截面并对截面属性进行测量得到Sg=808.24 mm2。

则：

SP=8 167.14-808.24=7 358.9 mm2

将推力F3换算成压差Δp为：

根据连续性方程可知：

Q1=Q2=vgSg

式中：vg为过流速率。

根据节流压降公式：

式中：α为阻力系数，将孔口简化为圆柱形孔口，取α=0.5；ρ为液体密度，以水的密度计算则ρ=1×103kg/m3。

由以上两式，可得：

2.3 开启滑套所需流量计算

滑套开启时，液体推动球，球在液体作用下推动弹性套，弹性套再推动内滑套，完成开启动作。为了防止内滑套在其他施工过程中因节流压差推动误开启，在内滑套上安装了剪切销钉。因此，滑套开启时，弹性套要克服2个力作用，分别是2.1节中的弹性套自身移动的力和内滑套上剪钉剪切力。

根据压裂施工最大排量360 m3/h计算并选取剪钉，最终确定剪切力为F4=259 N。滑套开启时，弹性套受力为：

F5=F3+F4=1 039.8+259=1 298.8 N

计算节流压差为：

计算滑套打开所需排量：

2.4 弹簧力计算

在可变径球座位置设计复位弹簧。弹簧作用是将可变径球座从球座滑套中拉出，其克服第2.1节中计算出的力f=73.5 N。

参照图11a，弹簧的安装高度为178 mm，弹簧丝直径为ø7 mm，弹簧的中径取值ø105 mm。参照图11b，压裂球推动球座滑套到极限位置后，最大工作载荷时弹簧的高度为83.5 mm。参照图11c，压缩弹簧推动可变径球座从极限位置到最小工作载荷位置，此时弹簧的高度为132.5 mm。

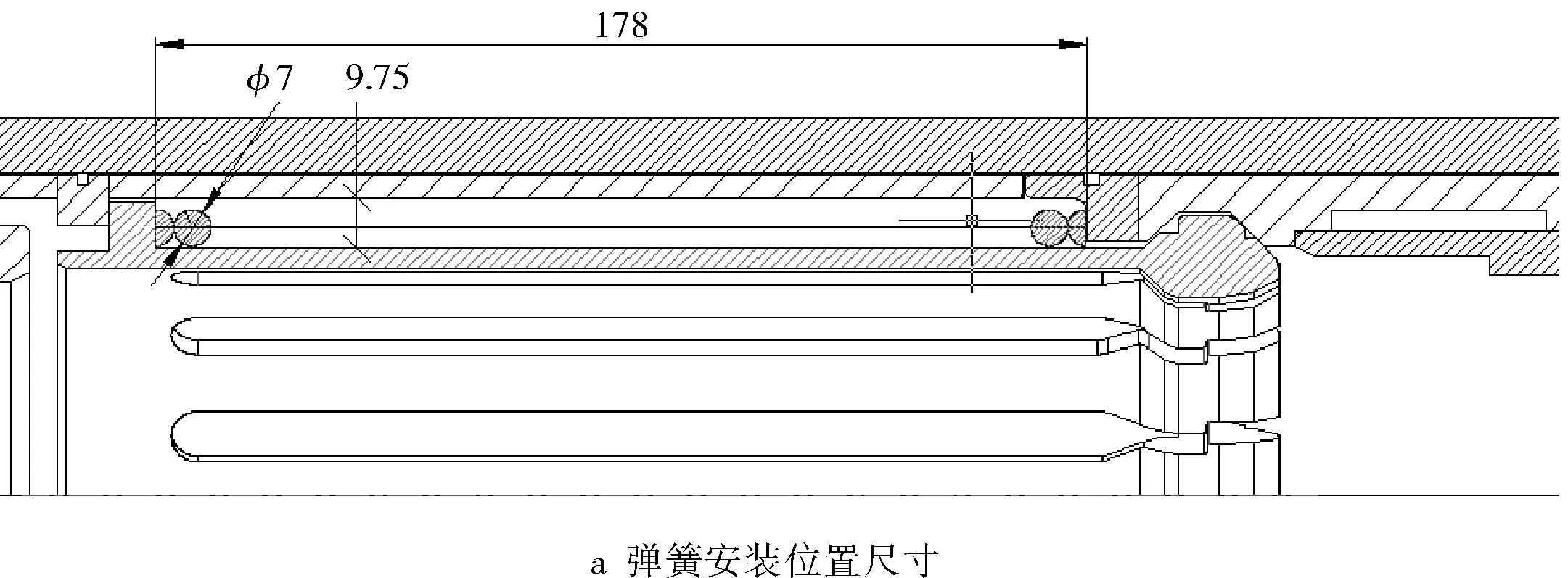
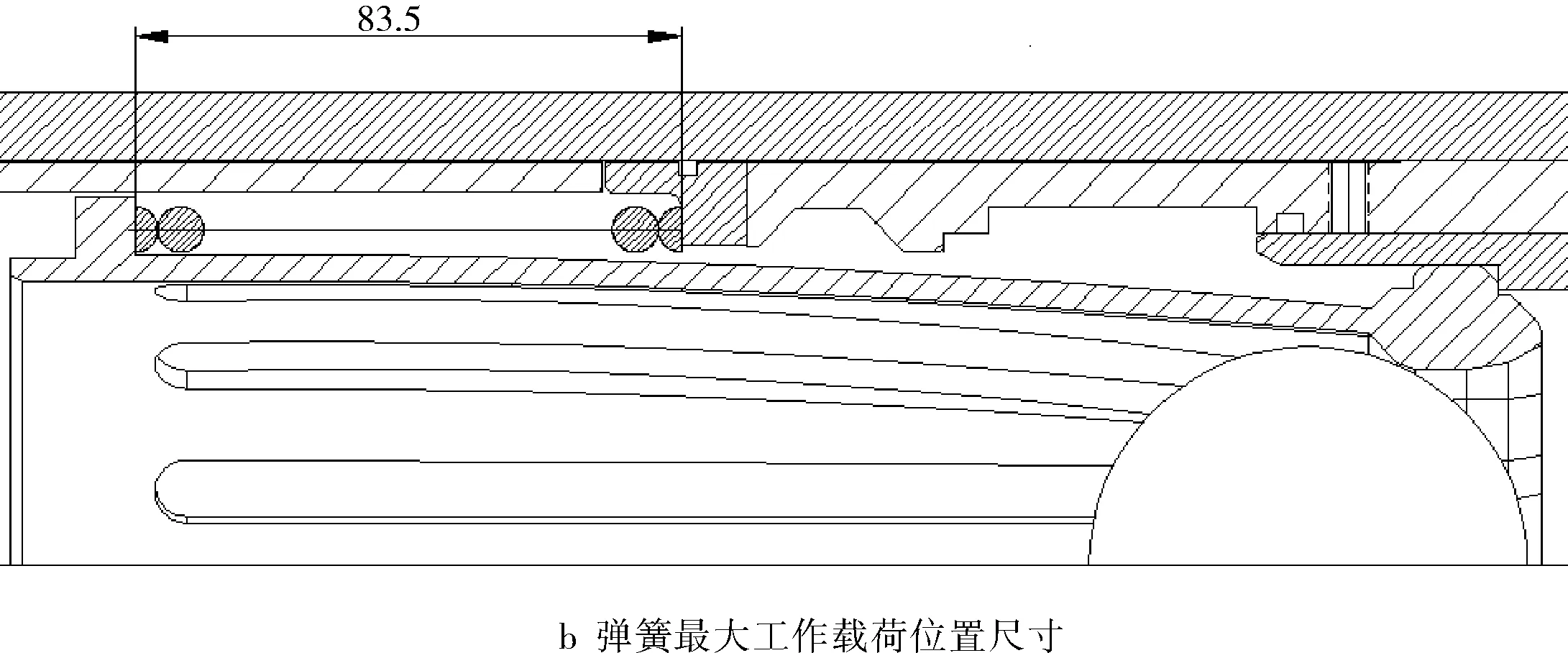
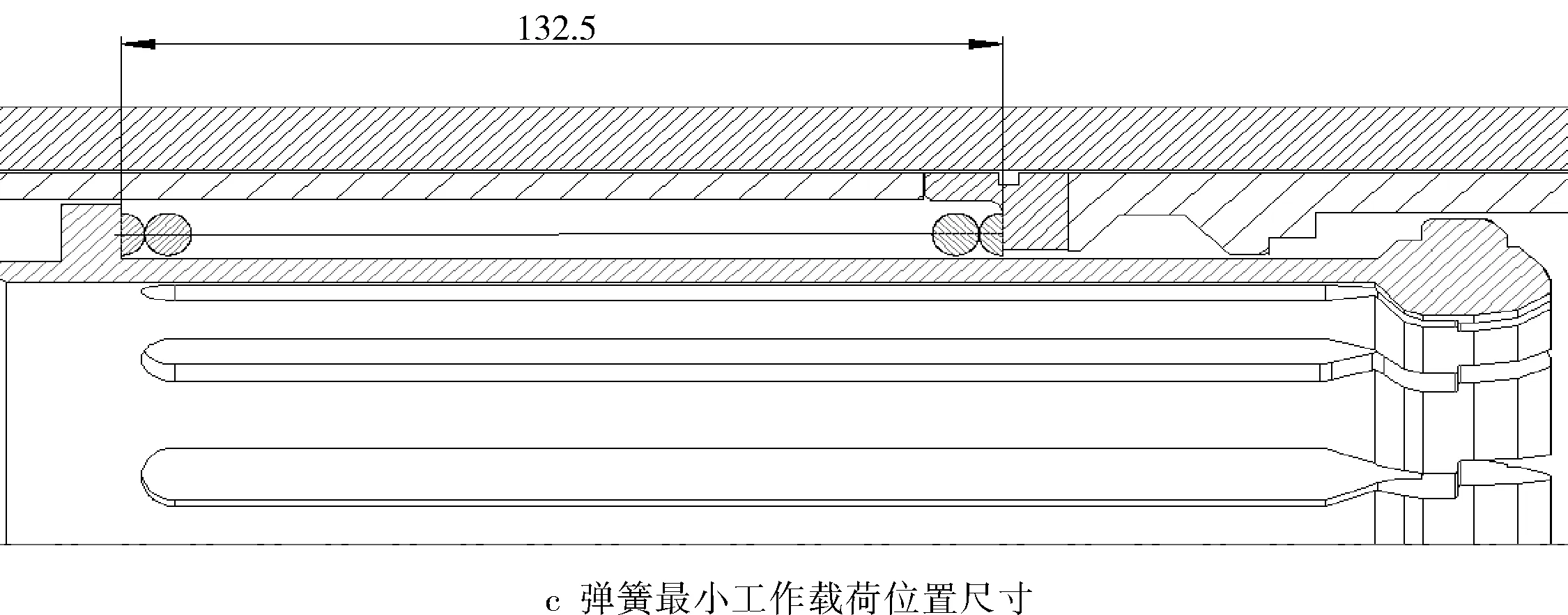
图11 弹簧受力分析

根据以上计算并确定弹簧的基本参数如下[10]：

弹簧的旋向 右旋

弹簧的材料 65 Mn

弹簧的自由高度 185 mm

弹簧的钢丝直径 7 mm

弹簧的中径 105 mm

有效圈数 5.5圈

弹簧的结构 两端压紧磨平，支撑圈数1圈

弹簧的热处理硬度 HRC43～48

弹簧的有限元应力分析结果如图12所示。

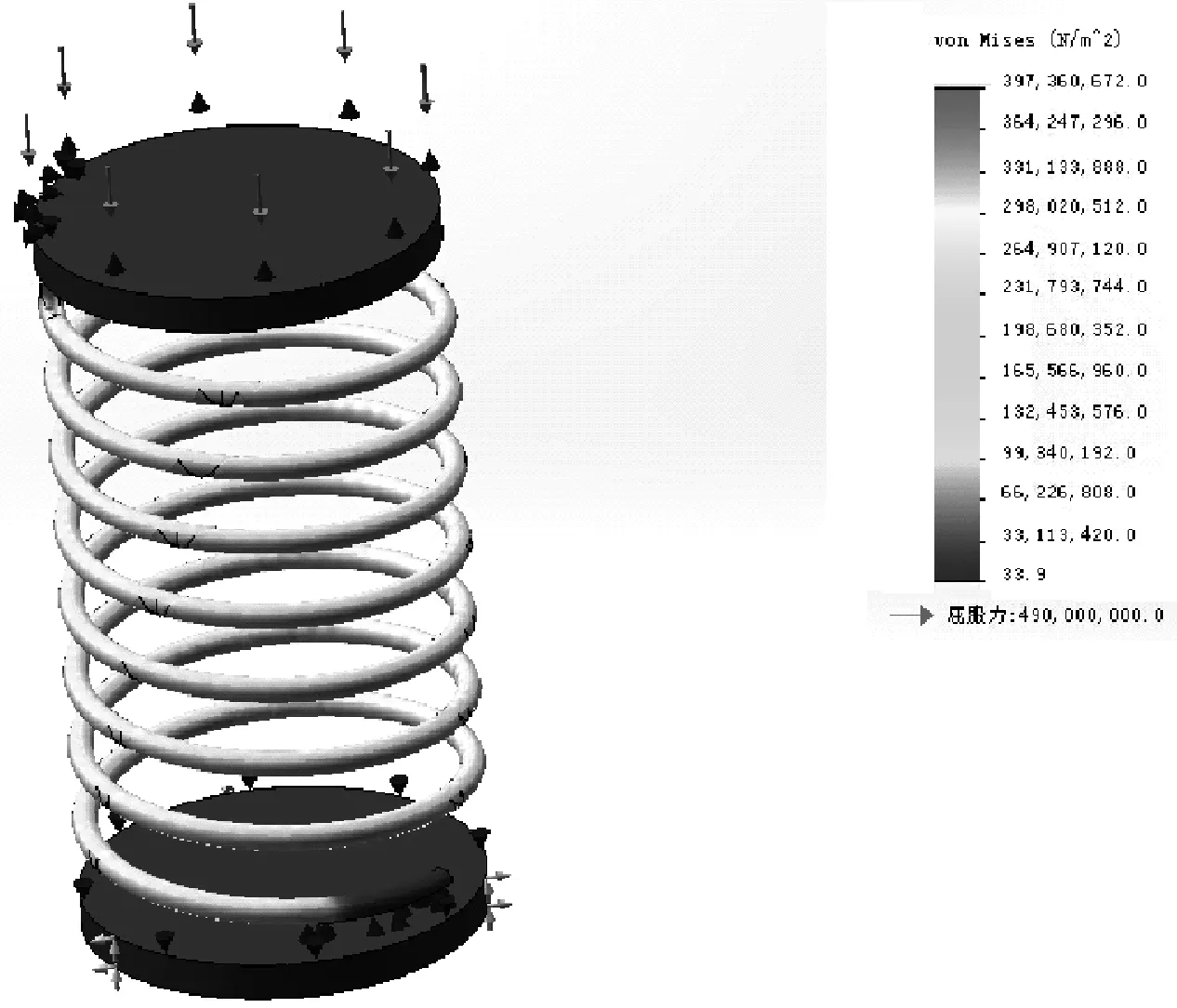
图12 弹簧的应力云图

复位弹簧最大应力值出现在靠近上端第3圈附近，且未超过其屈服强度，强度满足要求。

3 室内试验

3.1 机械驱动过球试验

机械驱动过球试验装置如图13所示。通过机械驱动过球试验，验证分段压裂滑套的动作完整性。试验步骤为：

1) 依次把4个滑套连接在一起，安放在上扣机中，并用上扣机夹紧。

2) 用连杆将4只球连接起来，然后与上扣机的推拉机构连接。

3) 用推拉机构将压裂球推送进滑套内，观察4个滑套是否按顺序依次开启。

按既定方案连接好滑套，把压裂球用刚性连杆串接，然后与拉力传感器连接，再与上扣机的推拉机构连接，测得打开滑套的力为1 050 N，4个滑套全部开启。

3.2 压裂液开启滑套试验

压裂液开启滑套试验装置如图14所示。试验步骤为：

图13 机械驱动过球试验装置

1) 依次把4个滑套连接在一起，通过变扣与压裂泵连接。

2) 开泵，从排量1 m3/min开始观察，直到看见滑套本体出口开始出液为止，记录此时泵的排量和压力。

3) 一旦观察到一级滑套开启并开始出液，停泵，卸开工具与泵连接位置。然后，把第2个压裂球投入管串中(如果有投球口，可直接从投球口中投入压裂球)，再接上泵。开泵，以不低于上一步打开滑套的排量进行试验，直到看到二级滑套的出口有液体排出，停泵。

4) 继续投球，依次重复作业，直到所有滑套开启并有液体排出，试验即可结束，功能试验完成。

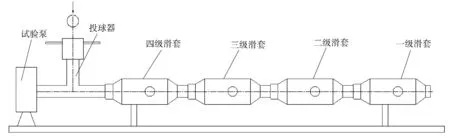
图14 压裂液开启滑套试验装置

按既定方案连接好滑套，并将滑套与泵连接。所用压裂液参数为：清洁压裂液，黏度110 mPa·s，压裂砂粒径为30～50目[12]。试验结果表明，滑套全部开启时排量为80 m3/h。

4 结论

1) 分段压裂滑套没有级差缩径，整个压裂管柱使用同一种尺寸的压裂球来打开滑套，理论上分段数量不受限制。

2) 通过理论计算和有限元分析，滑套关键零部件满足强度要求。

3) 室内试验验证了滑套开启性能。通过混砂压裂液驱动开启滑套试验，滑套需要的最小开启排量为80 m3/h，该数值与理论计算值相吻合。

4) 该装置及其配套工艺管柱为无限级分段压裂提供了一项新技术，可广泛应用于海上低渗和陆上非常规油气藏压裂增产作业。