钻柱粘滑振动仿真和控制策略研究
2022-06-17陈午阳刘曙光胡小雄
陈午阳,刘曙光,胡小雄
(1. 黄山学院 机电工程学院,安徽 黄山 245800;2.中国科学院 宁波材料技术与工程研究所,浙江 宁波315211;3.星宇电子(宁波)有限公司,浙江 宁波 315514)
在深井石油钻探过程中,常发生极具破环性的钻柱粘滑振动,严重时会造成钻杆钻速降低、组合钻具失效,甚至钻杆断裂[1]。如何消除钻井中的粘滑振动成为亟需解决的工程难题。导致这些振动的主要原因包括:钻杆与井壁间摩擦、钻头与岩层剪切面之间的接触摩擦、井眼偏斜、钻杆旋转不平衡、及各种线性或非线性的共振[2-3]。
随着井深的增加,岩石的塑性和硬度增大,钻杆的扭转刚度相对降低[4]。由于钻头很难克服岩石、砂砾产生的静摩擦转矩,在短时间内钻头会产生停钻、卡钻现象,此时为钻头的粘滞阶段[5]。顶驱或转盘一直带动钻柱及井下钻具转动,当积蓄在钻柱中的扭转势能足以破坏岩层时,钻头上积累的驱动力矩就会非常大。当驱动力矩超过井下岩石与钻头产生的摩擦力矩时,钻头会突破粘滞,进入滑脱状态,并在正反方向上加速或减速,有时钻头的角速度会达到顶驱电机转速的数倍[6-7]。如此大的扭转冲击,如果超过设备所能承受的极限转矩,危险情况下会迫使钻井设备停止运行。
本文依据二自由度弹簧-扭摆钻柱动力学模型,推导出钻头运转状态方程,设计一种转速负反馈闭环调节和转矩负反馈闭环调节的双闭环控制方法[8-9]。此方法能及时调整顶驱电机转速,改善井底钻具组合运转状态,达到抑制滑钻或卡钻的目的。
1 钻柱粘滑振动力学模型
1.1 数学模型的建立及分析
钻柱结构分外圈和套管,而钻柱处在内外有钻井液的封闭环境中。由于单个钻杆的直径很小,会使钻出的井眼很小。钻杆在地面装置的驱动下,会受到井底地层各种岩石的作用力。除此之外,还会受到钻头与岩层砂砾相互作用的干扰力,以及钻柱本身的惯性力。综合分析钻柱系统具有的复杂性,不利于建立模型。为此做以下简化:
1) 不考虑横向振动和纵向振动与扭转振动产生的耦合效应,单单考虑扭转振动[10-11]。
2) 对钻柱系统进行抽象性处理,将其等效成顶驱电机和转盘。
钻具组合和钻头的二自由度数学模型如图1所示。

图1 钻柱二自由度扭转摆模型
按照图1中的等效模型,根据旋转刚体力学原理,可得顶驱转盘的运动方程:
(1)

Tt和Tar的表达式:
(2)
Tar=crωr
(3)
式中:cr为顶驱阻尼系数;c为等效粘滞系数;k为等效刚度系数;φr为顶驱旋转角度;φb为下部钻组合旋转角度;ωr为顶驱转盘的角速度。
建立钻柱系统的运动学方程:
(4)

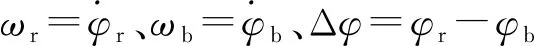
(5)
用状态空间方程改写式(5)得:
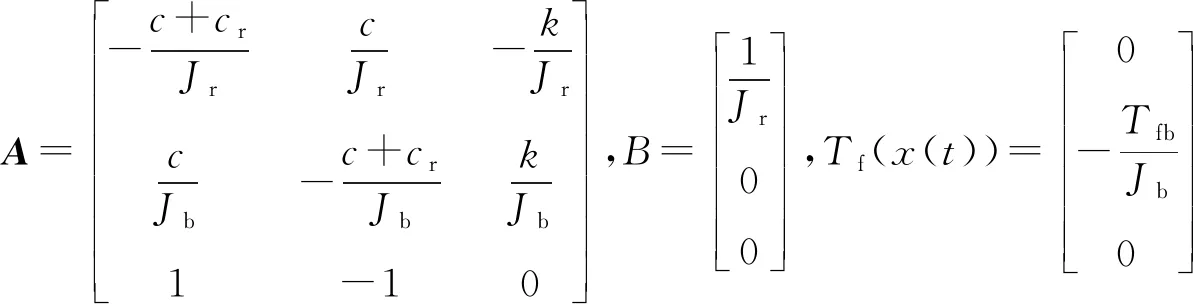
(6)
在顶驱转速保持不变的情况下,式(6)可变换为式(7):
(7)
通过以上数学公式对钻柱扭转行为的描述,发现粘滑振动现象的产生与等效阻尼系数和等效扭转刚度系数有关,其根本的关系是钻杆的长度。当钻杆长度增加时,扭转刚度系数降低,粘滞阻尼系数加大。若此时不增加电机转速或者降低钻压,底部钻头将会发生粘滑现象。为进一步获取粘滑振动的行为状态,可借助Simulink模拟器观测钻头的转矩和转速的变化情形。
1.2 二自由度的建模仿真分析
为使建立的钻柱数学模型中,顶驱给定的转速值与转矩值和钻头的转速与转矩的关系曲线凸显出来,使用了MATLAB工具。在Simulink编辑器中建立二自由度的钻柱数学模型,仿真粘滑的产生过程。借助Simulink中的示波器元件实时显示钻头的动态响应曲线,并借助该曲线给定顶驱电机不同的转速值,对不同状态下的钻头速度和转矩进行实时分析。以下将通过转速控制模式进行系统地分析。
依据式(7)中得出的钻头角速度ωb和顶驱驱动转矩Tm的计算公式,分别给定输入顶驱转速值ωr=4 rad/s和ωr=8 rad/s,分析对比钻头的转速和转矩的状态曲线。图2所示为转速模式控制下,二自由度的Simulink建模仿真框图。

1-输入电机转速ωr;2-ωb与ωr角速度差;3-等效粘滞系数c;4-积分器角度差;5-等效刚度系数k;6-顶驱阻尼系数cr;7-顶驱转盘和钻具组合之间的耦合力矩Tt;8-顶驱输出转矩Tm;9-静态平衡力矩Teb;10-Teb与Tfb扭矩差;11-钻头阻尼系数cb;12-钻头角加速度;13-积分器钻头角速度;14-钻头扭矩。图2 速控模式下仿真框图
通过改变ωr值,对钻头角速度ωb和钻头转矩Tfb进行分析。当ωr=4 rad/s时,Simulink仿真结果如图3所示,钻头出现周期性地粘滞与滑脱现象,其最高转速可达顶驱转速的2倍以上,这与理论研究的数据贴合。在图3b中,钻头的转矩波动出现大幅度的震荡,有时会出现负值,显然钻头的转速和顶驱的力矩会随着钻头的非线性摩擦力矩的波动而上下大幅震荡,此时钻柱系统已出现粘滑振动。
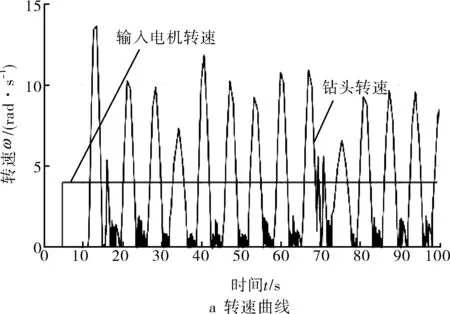
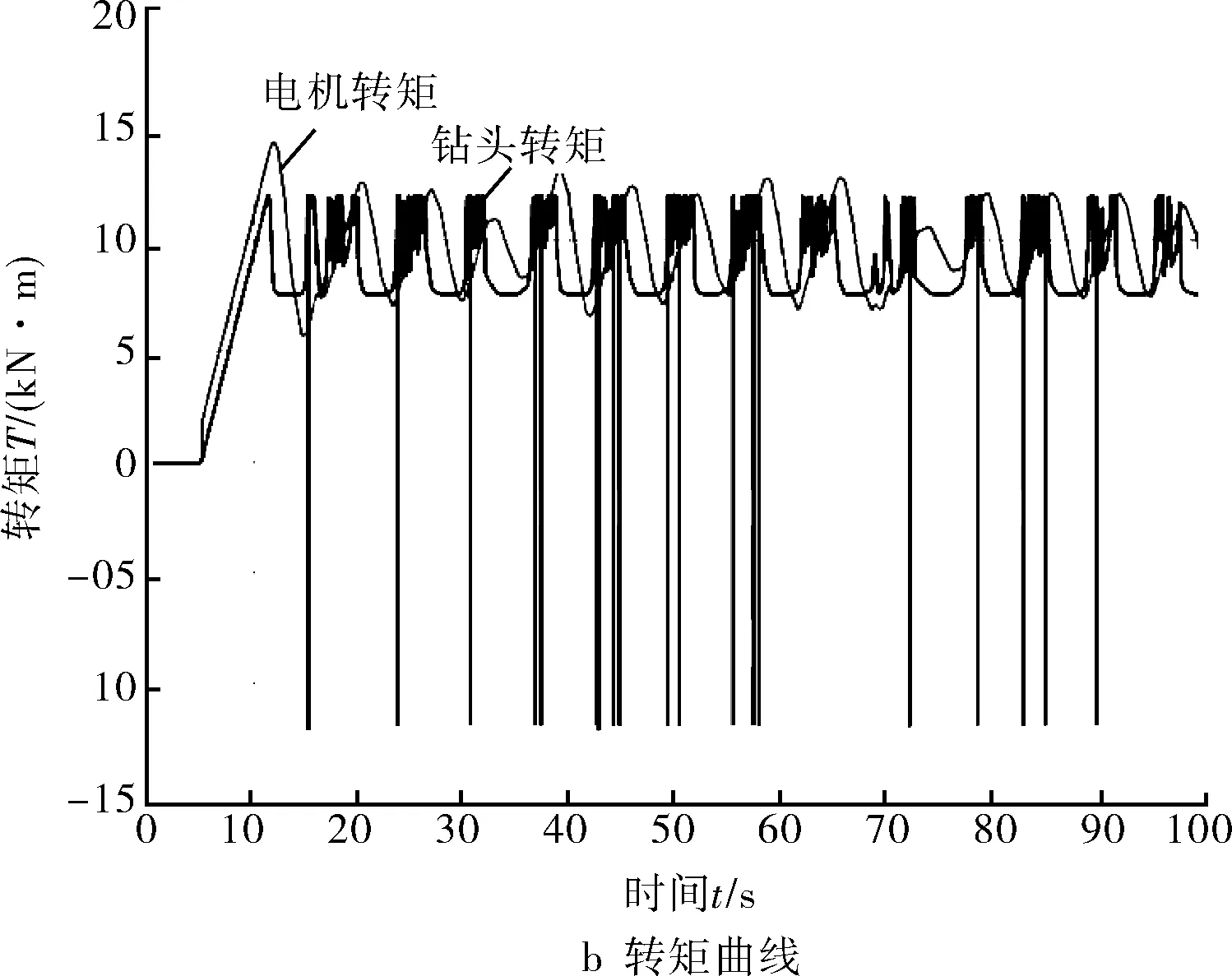
图3 ωr=4 rad/s时转速-转矩仿真结果
当给定转速值ωr=8 rad/s,仿真结果如图4所示,钻头的转速和顶驱力矩出现短期的振荡,有粘滑现象产生。但是,随着时间的推移,最终钻头钻速与转矩值趋于恒定,钻头处的转速与顶驱转速最终相同,说明钻头处的摩擦转矩为滑动摩擦转矩。此时系统的粘滑振动消除。结合前一组数据对比,可知增大顶驱转速,可以减小粘滑现象。
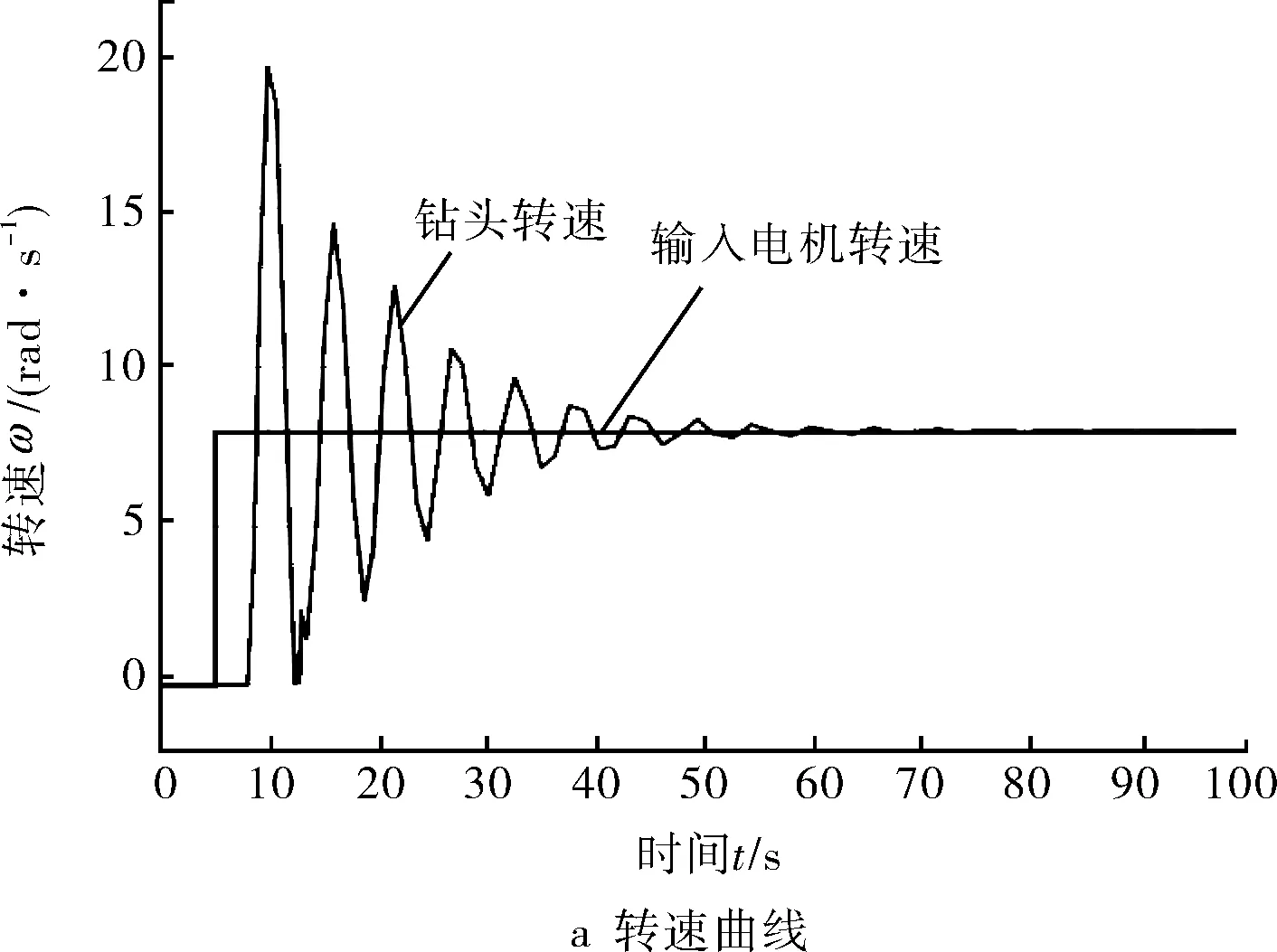

图4 ωr=8 rad/s时转速-转矩仿真结果
通过对钻柱系统简化模型分析,结合仿真波形的规律可知:当井下的钻杆长度超过其临界长度,对于一定转速,将会产生粘滑振动。减小钻杆等效刚度系数,或增大钻杆粘滞阻尼系数,会使粘滑振动的周期延长,振幅加大。提高顶驱转速,或降低钻头钻压,可有效地消除粘滑振动现象。
2 PID自适应控制策略
2.1 PID控制器简述
PID控制器是一种线性控制器,它根据给定值r(t)与实际输出值y(t)构成控制偏差[12],即:
e(t)=r(t)-y(t)
(8)
对于计算机处理的采样数据来说,它是基于采样时刻点kT的偏差值来计算控制量。在此基础上需对偏差公式进行离散化处理。现在以采样时刻点kT(k=0,1,2,…,n)代替连续时间t,以和式代替积分,以增量代替微分,则可做如下近似变换:
可得离散的PID表达式为:
(10)
式中:T为采样周期,在模型计算中要使T值足够小,且满足香农采样定理,方能保证系统有一定的精度;k为采样序号,k=0,1,2,…n;e(k)为第k次采样时刻输入的偏差值;e(k-1)为第k-1次采样时刻输入的偏差值;u(k)为第k次采样时刻计算机的输出值[13]。
2.2 双闭环自适应控制策略
在实际的钻井过程中,由于井底运转条件复杂,检测装置采集的信号经长距离传输后精度变低,钻头的状态无法通过硬件检测装置获取检测信息。因此直接将钻头作为被控对象的双闭环调节控制系统将无法实现预想的控制效果,必须采取其他措施对其改进。
结合前面建立的钻柱动力学模型,依据钻柱动力学建模中的各类参数,计算出钻头的速度状态值和所受摩擦转矩数值,反馈给顶驱电机。并且当底部钻头受到岩石摩擦阻力较大而产生粘滑振动时,顶驱电机的转速和转矩也发生相应的响应。此响应是可通过顶驱电机变频器实测的数据。依据动力学建模的钻头参数与实测参数相结合得出速度的补偿信号,作为双闭环控制调节系统的反馈补偿,使顶驱电机的转速得到改变,变化的电机转速信号传递给变频器,变频器调节电机的主轴转矩,进而使主轴转矩值发生变化,改变井下的运转状态,调节钻柱的扭转能量,抑制粘滑振动的产生[14]。为此,在转矩负反馈的基础上提出转速-转矩双闭环负反馈调节控制系统。
图5为基于PID控制的双闭环控制策略系统图。双闭环的意思是具有2个闭合回路,内回路为转矩环,称为副回路;外回路为速度环,称为主回路。主副回路各有调节控制器和限幅器。主回路中由检测装置获取拖动电机的转速值,乘上增益系数α,得出给定速度参数nf=α·ng,经PID控制器和限幅器输出给转矩给定值;而副回路中从执行器中检测出的转矩值Tg,乘上增益系数β,得出另一转矩给定参数Tf=β·Tg,经PI控制器和限幅器输出给执行器和电机。主调节器与副调节器以串级的方式进行共同控制,故称为串级联动控制系统。由于主调节器的输出作为副调节器的给定值,因而串级控制系统的主回路是1个恒值控制系统,而副回路可以看作是1个随动系统。串级控制系统在结构上比单回路控制系统多了1个副回路,因而对进入副回路的二次扰动有很强的抑制能力[15-16]。
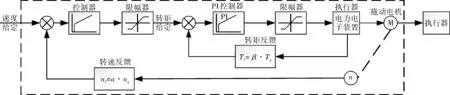
图5 双闭环控制策略系统框图
2.3 双闭环控制效果图
由上文所述的双闭环控制策略,在Simulink仿真软件上画出仿真框图,如图6所示。
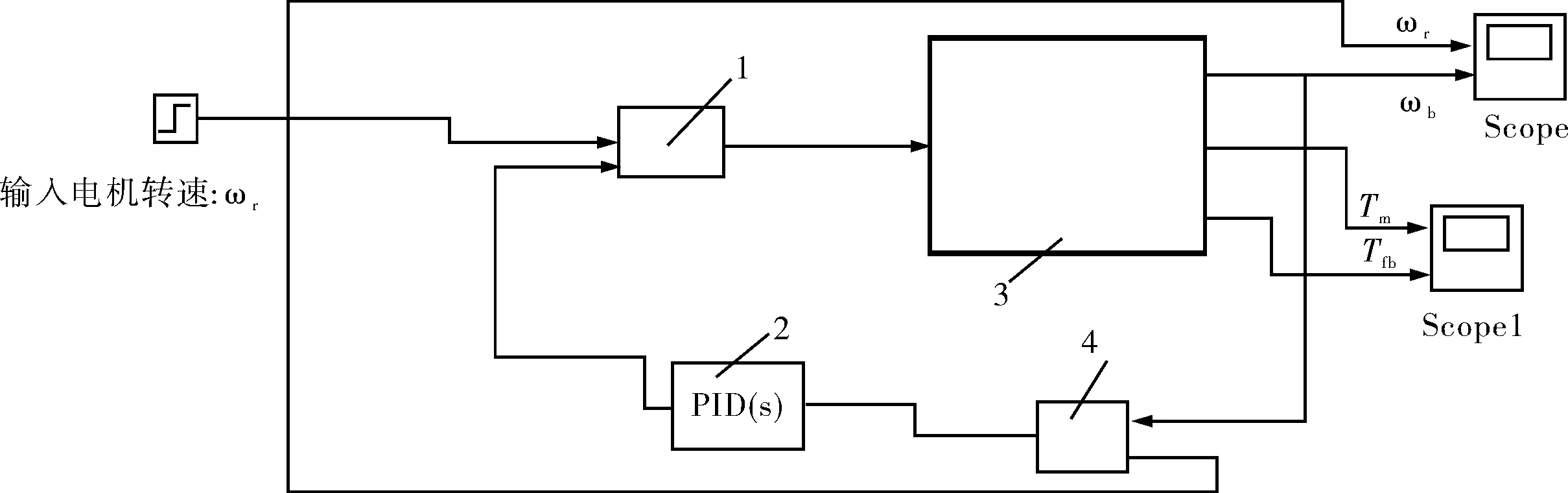
1-积分调节角速度差;2-PID控制器;3-钻柱动力学系统;4-初始角速度差。图6 PID控制建模仿真框图
当选取PID控制策略,设定参数P=2.1,I=0,D=0时,钻头的转速和转矩值的变化曲线如图7所示,可知,在3~4个周期内,转速和转矩值均趋于平稳状态,说明以输出的钻头转速作为检测值,与给定转速作差作为PID控制器的输入端,得到的最终偏差值加到给定的顶驱转速上,使顶驱电机输出调整的速度波形,可以有效地消除粘滑振动现象。但细微地观察会发现,钻头的转速和转矩值会有轻度的波动,这是源于单个P值引起的调整振荡。

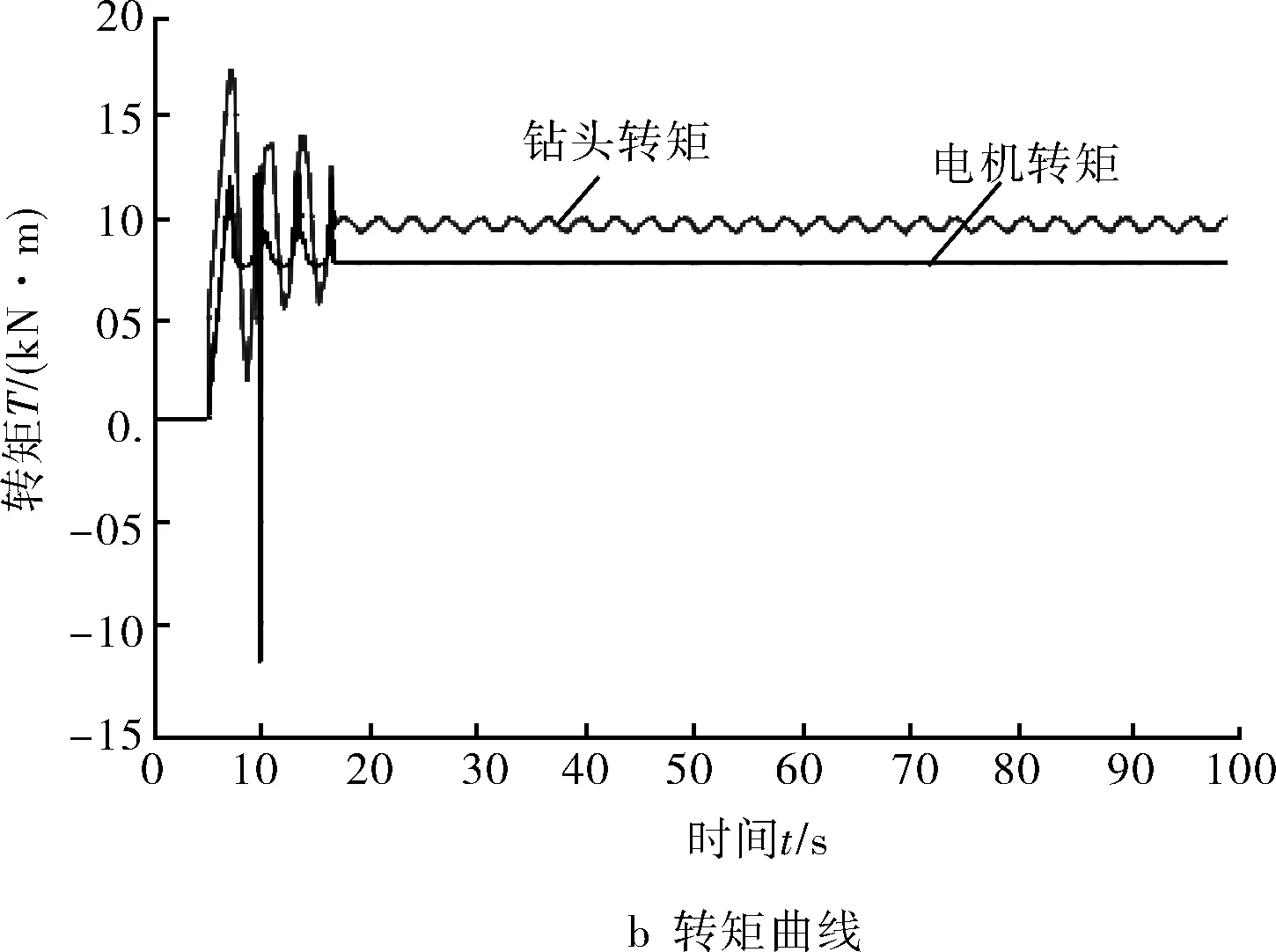
图7 转速-转矩仿真结果(P=2.1,I=0,D=0)
当选取P=2.1,I=0,D=0.8时,软转矩控制效果如图8所示,可知,钻头钻速和转矩可以很快达到控制效果,而且消除了调整单个P值引起的振荡现象,此种情况为控制的理想状态,从另一方面也验证了PID控制策略的可行性与优越性。
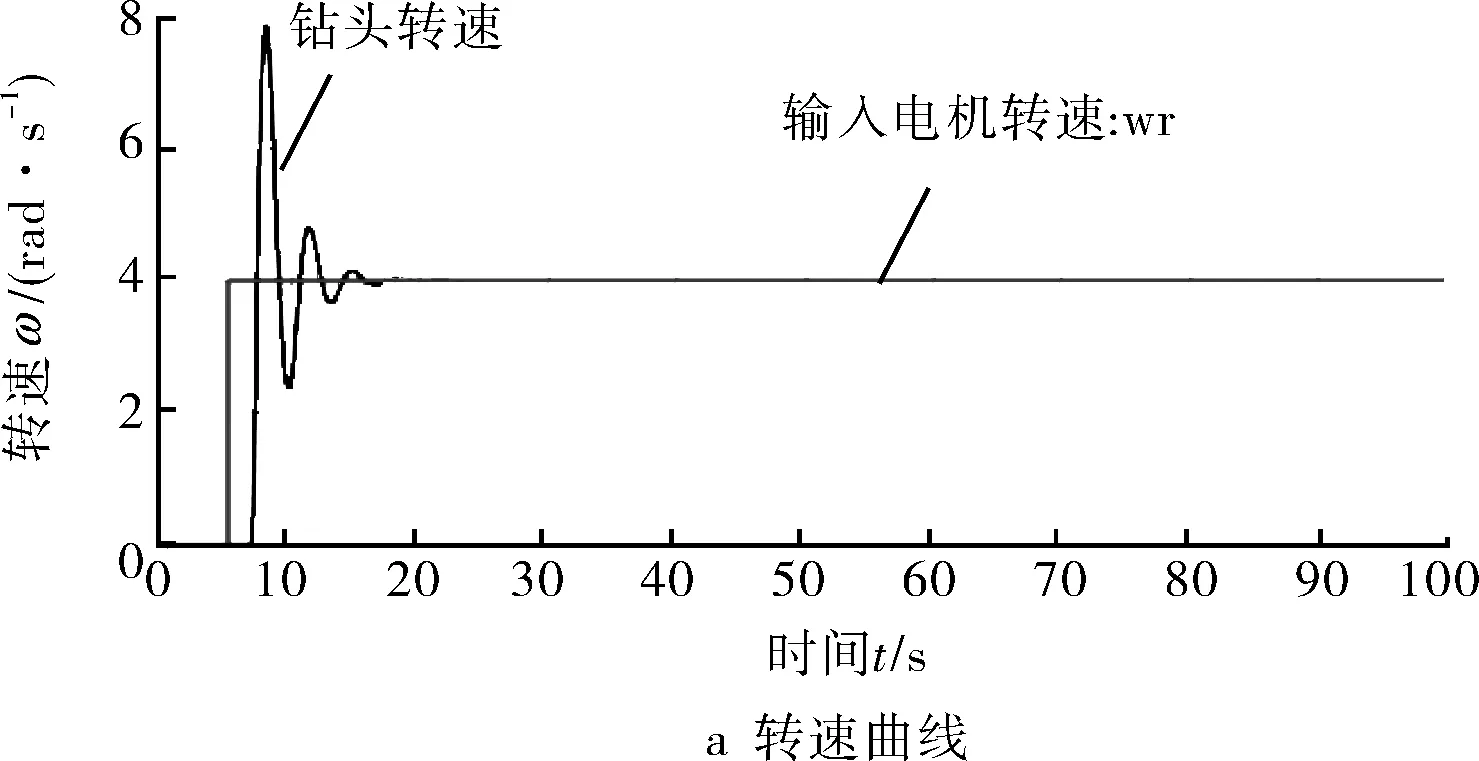

图8 转速-转矩仿真结果(P=2.1,I=0,D=0.8)
3 结论
1) 本文阐明了钻柱粘滑振动产生机理。建立了二自由度的钻柱动力学模型,得出钻头的状态方程,并仿真出粘滑时的钻头状态曲线。
2) 基于顶驱电机转速与钻头转速的函数关系,提出转速-转矩双闭环调节控制策略,并由仿真结果验证了控制策略的可行性。综合试验结果表明,反馈调节的顶驱转速能够在3~5个周期内有效地抑制钻柱粘滑振动。
