基于POD-Galerkin 降维方法的热毛细对流分岔分析1)

郭子漪 赵建福 李 凯 胡文瑞

(中国科学院力学研究所微重力重点实验室,北京 100190)

(中国科学院大学工程科学学院,北京 100049)

引言

热毛细对流是由温度梯度导致的界面张力梯度驱动的对流,是空间自然对流的基本形式.作为一个流动与传热耦合的复杂非线性过程,随着驱动力的增加,热毛细对流会由稳定的层流,经历各种各样的分岔,发展为混沌流.热毛细对流的转捩过程受几何形状、热边界条件和物性参数等多种因素的影响[1-2].以往的实验[3]及数值模拟中研究了各种工况下的热毛细对流,对临界[4-6]及超临界转捩过程得到了丰富的结果,确认了热流体波的振荡形式[7],发现了倍周期分岔,准周期分岔,切分岔等转捩途径[8-10].然而,大多数的数值模拟研究采用直接数值模拟的方法,需要在不同参数下进行大量数据计算,不但难以获得完整的分岔图,而且效率不高.近年来,基于动力系统中的分岔理论[11],发展出了一套数值分岔方法[12],通过求解分岔方程,计算分岔点,得到更为完整的分支图,此方法在流体力学的许多领域得到了成功的运用[13-16].但是,由于流动的控制方程是偏微分方程组,空间离散后化为维数极高的常微分方程组,这为准确及高效求解带来了困难.为了解决这一问题,除了尝试发展适用于大规模计算的数值方法,还可以考虑对原方程进行降维,在低维模型上进行数值分岔的计算.

常见的基于流场特征提取的降维方法主要有本征正交分解(POD)和动力学模态分解方法[17](DMD).POD 方法的本质是寻找高阶系统的一组正交基,满足原始流场在这组基上的方差最小,这个优化问题最终转化为矩阵的特征值和特征向量的求解[18],其中特征值反映各个模态的能量,通常少数几阶模态就占绝大部分能量,将流场表示为上述主要模态的线性组合,从而实现降维.DMD 方法的本质是将流动的演化看作线性过程,假设前后时间步的流场相差一个线性变换.并通过快照矩阵估计变换矩阵的特征值和特征向量,构造反映流动特性的动力学模态.由于DMD 方法对流动演化的过程进行分析,得到的模态是时空耦合的,不需要额外建立方程就可以估计流动随时间的发展[19].

与DMD 方法相比,POD 方法无法计算流动的演化过程,要想得到低维方程,需结合Galerkin 投影法,将原系统的解表示为特征模态的线性组合,利用POD 模态的正交性,通过Galerkin 投影将原偏微分方程化为以组合系数为未知量的常微分方程,上述构造低维方程的方法一般被称为POD-Galerkin 降维法.POD-Galerkin 降维法的有效性在许多研究中得到了验证:文献[20]构建了二维矩形腔内浮力对流的POD 降维模型,研究了不同模态数对模型稳定性的影响;文献[21]采取了混合不同参数下DNS 数据的方法,构建了三维圆柱绕流的POD 低维模型;Cai 等[22]研究了二维方腔内浮力对流的修正低维模型,并通过参数外推,验证了模型的鲁棒性;冯俞楷[23]等以优化POD 解的梯度为目标,从温度场的梯度中提取出最优正交基,结合Galerkin 投影法,建立了二维、常物性、非稳态导热微分方程的PODGalerkin 降维模型;Jing 等[24]利用三维方腔内浮力对流的低维模型进行数值分岔的计算,并与直接数值模拟的结果做了对比.

值得注意的是,大多数工作都是将POD-Galerkin 降维方法用在比较典型的顶盖驱动流、圆柱绕流、浮力对流等模型中.降维方法在热毛细对流中的运用鲜见.热毛细对流与上述流动的一个重要区别在于边界条件是速度和温度强烈耦合,普适的POD 降维方法可能不能直接应用.本文工作采用直接数值模拟方法,获取二维有限长液层热毛细对流的流场和温度场数据,并利用POD-Galerkin 降维法构建低维模型,通过数值积分和数值分岔的计算,在低维模型上研究流动的分岔特性,并与直接数值模拟的结果比较,验证模型的准确性和鲁棒性.目的是建立适用于热毛细对流研究的,由直接数值模拟、POD-Galerkin 降维和数值分岔三种方法优势结合的分岔分析流程.

1 数值计算方法

1.1 直接数值模拟

考虑如图1 所示体积比(Vr) 分别为0.95,1.00,1.05 的二维有限长液层中的热毛细对流,其中体积比定义为液层两端高度固定时,实际充液体积与界面平直时液体体积之比.本文假设流体不可压,忽略流动过程中界面形状的变化.

图1 有限长二维液层模型Fig.1 Limited liquid layer model

模型的无量纲参数为:宽度Ax=3,高度Ay=1,普朗特数Pr=4.4.

无量纲控制方程(以体积比为1.00 的情况为例)

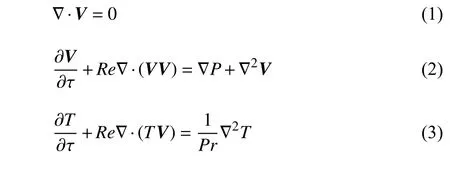
其中,V=(u,v),Re为雷诺数.

速度边界

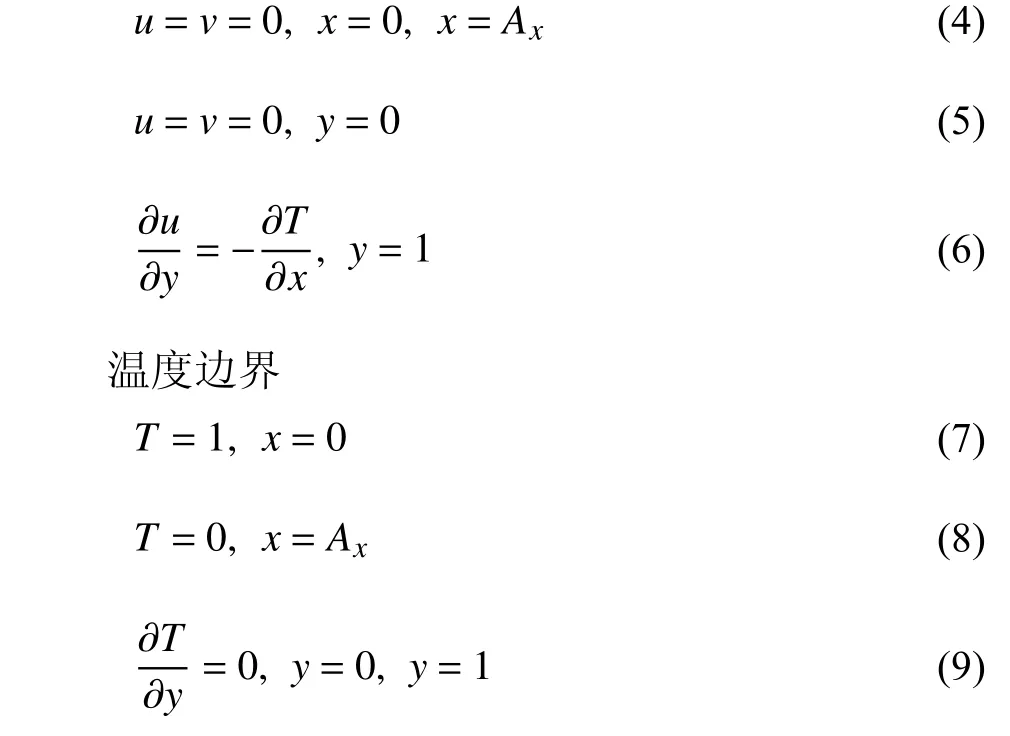
界面位形通过求解杨-拉普拉斯方程得到,采用同位网格有限体积法,利用贴体坐标变换,在计算域中离散方程,对流项用二阶中心差分离散,压力和速度的耦合用SIMPLE 算法,时间步长为0.000 1.

1.2 数值算法验证

采用非均匀网格,网格分布按照如下公式[25]

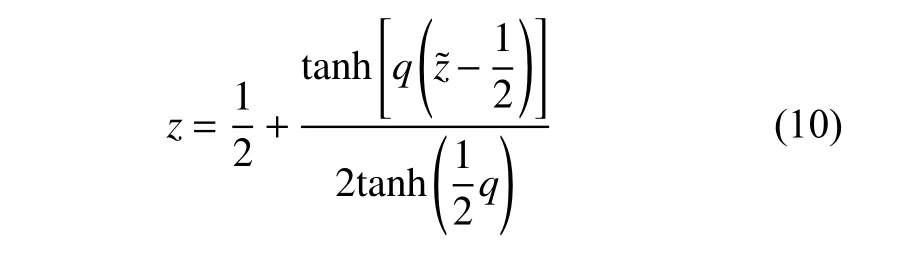
其中,q为拉伸参数,为均匀的网格点.

表1 列举了Vr=1.00 时不同网格数下计算的临界雷诺数,当网格数为60 × 20 (非均匀q=2)时,临界Re与文献[26]中的误差在1%左右,所以在之后的计算中采用的x方向网格数为60,y方向网格数为20,参数q=2.

表1 直接数值模拟算法验证Table 1 Verification of DNS method

1.3 POD-Galerkin 降维法

1.3.1 本征正交分解

本征正交分解方法利用直接数值模拟或实验得到的流场数据,构造一组规范正交的特征模态,以此反映流动的相干结构.各个特征模态的能量占比不同，一般少数的几阶模态就包含了流场的大部分能量,可以反映出主要的流动特征.具体分解过程如下[24]:

由直接数值模拟的数据计算某一时段内速度场和温度场的时间平均量及扰动量

利用扰动量构造快照矩阵

其中,m,n=1,2,···,N,内积定义为(a,b)=,D为物理空间,当a,b为向量时,点乘表示向量的点乘;当a,b为标量时,点乘表示普通的乘法.

由于相关矩阵是实对称矩阵,可以求出它的一组规范正交的特征向量及对应特征值

利用快照矩阵和特征向量构造特征模态

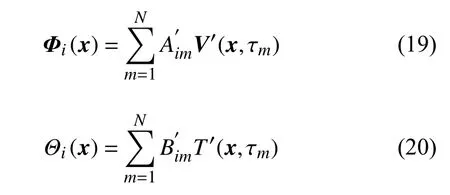
其中

事实上,这样得到的特征模态在前面定义的内积意义下,也是规范正交的.

1.3.2 Galerkin 投影法

Galerkin 投影法是将解用一组规范正交的基函数线性表示,代入控制方程,再将方程投影到基函数上,得到线性组合系数的常微分方程组.当取基函数为POD 特征模态,就是POD-Galerkin 降维方法,以本文所用模型为例,具体流程如下.

由原方程推出扰动方程

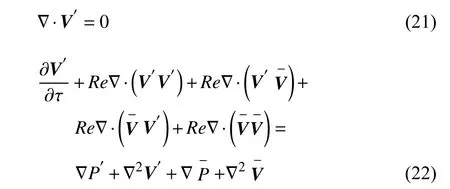
将扰动量表示为特征模态的线性组合,代入扰动方程

其中,MV,MT分别为截取的速度和温度的POD 模态数.

将扰动方程投影到各个模态上,由正交性,可得以模态系数为因变量,时间 τ 为自变量的常微分方程组,由于特征模态自然满足不可压缩条件,所以这里不考虑连续性方程.此外,压力梯度项在模态上的投影可化为

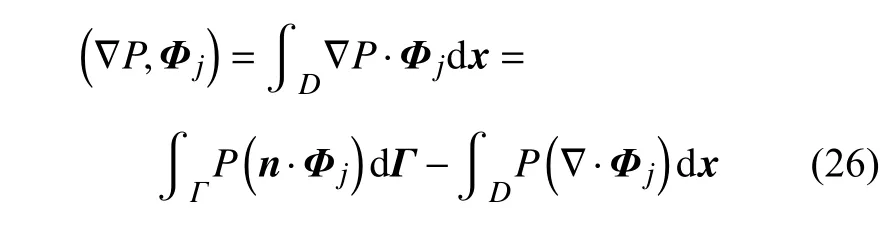
由于特征模态在积分区域内满足连续性方程,故式(26)第二个等号右端第二项等于0,而由于固壁边界条件为无滑移,无穿透,自由面随时间不变化,速度特征模态在各边界的法向分量均为0,故式(26)第二个等号右端第一项也等于0.所以,压力梯度项的投影为0,从而

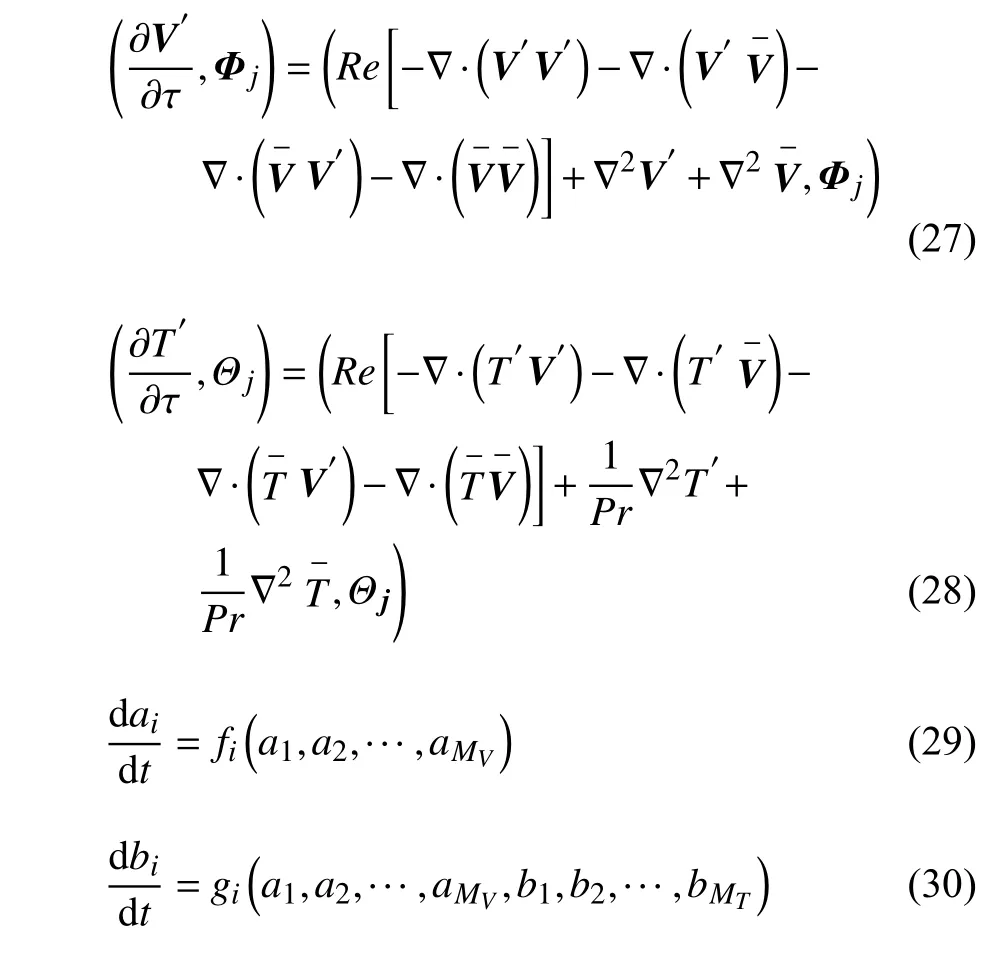
此时,方程组的维数等于截取的模态数,由此完成了对原高维方程的降维,可以很容易地求解这个低维方程,得到模态系数,重构出流场,这样就实现了流场的快速求解.

1.3.3 修正的POD 降维模型

POD 方法通过截取前几阶特征模态实现降维,忽略了通常起耗散作用的高阶模态,由这样构造出的低维方程求得的解往往不稳定,随着时间的增长,误差会逐渐累积.所以,为了提高POD 降维模型的长期预测能力,需要对模型进行修正,常用的修正方法有内在稳定性方法[27],谱黏性方法[28],涡黏性耗散模型[29]等,这里采用内在稳定性方法[27,30].

设原精确方程的动力系统和POD 降维系统分别为

具体实现中,需要把 ε (t) 投影到模态系数向量上,将其表示为

其中,M为模态数,N为快照数,〈 ·,·〉 表示向量的点乘.

最后得到修正的POD 降维方程

其中

1.3.4 速度场和温度场的耦合处理

需要指出的是,本文中的热毛细对流是速度场和温度场互相耦合的过程,因此需要对上述一般方法做一定修改:

首先,速度和温度的相关矩阵不作为独立的矩阵处理,而是将两个矩阵相加,对求和后的相关矩阵取特征向量和特征值

其次,速度和温度的特征模态的公式仍如前文所述,但是将速度和温度表示成特征模态的线性组合时,设它们的截断模态数(M)和组合系数均相同

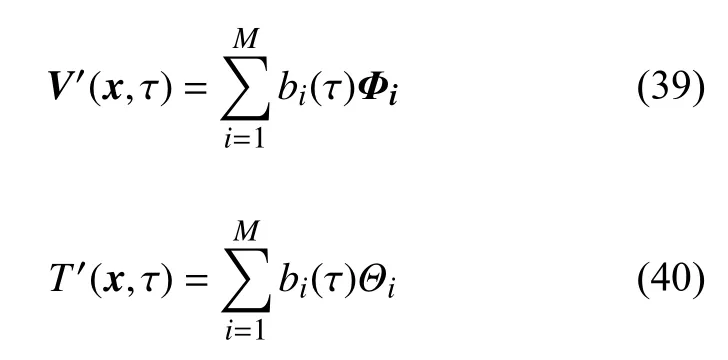
这样处理是考虑到自由面上的边界条件由速度和温度耦合表示,其各特征模态在构造低维方程时也要相对应,才能保证满足边界条件.

1.4 数值分岔算法

对于一个含参数p的动力系统=F(u,p),可以通过数值求解分支解和分岔点来研究系统的解随参数变化的分岔特性.

平衡点满足方程

一般用牛顿迭代法求解.

周期解满足方程(其中T为待求的周期)

添加一个相位的条件,可将其视为两点边值问题求解.

平衡点和周期解分支可由参数延续法(continuation method)得到,各类分岔点可通过对应的方程确定,详见文献[13-14].

2 计算结果

2.1 直接数值模拟结果

利用直接数值模拟,在不同Re下,计算了各体积比模型中的热毛细对流.随着Re的增加,流动经历了稳态到振荡再到稳态的发展过程,得到了Rec1,Rec2两个临界Re,如表2 所示

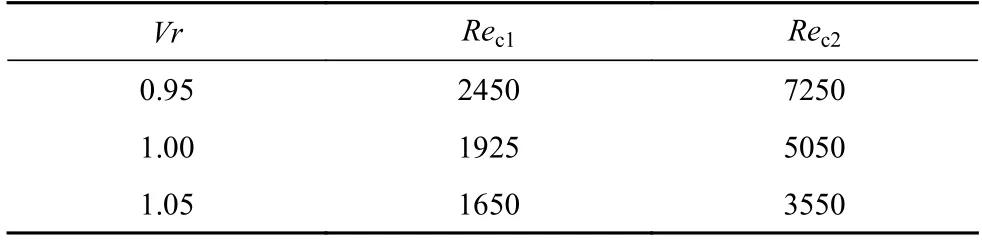
表2 各体积比下的临界雷诺数Table 2 Critical Reynolds number under different volume ratios

2.2 POD 降维模型计算结果

2.2.1 构造修正的降维模型

以Vr=1.00 为例,对Re=3500 提取振荡稳定后,无量纲时间间隔为0.01 的201 个速度场和温度场快照,进行了本征正交分解,对特征值按从大到小排序,并计算前n个模态的特征值之和占所有模态特征值之和的百分比,得到的能量占比随模态数的变化如表3 所示.

表3 不同模态数(n)下的能量占比(Re=3500,Vr=1.00)Table 3 The accumulative energy contribution of the first n POD eigenmodes (Re=3500,Vr=1.00)

随着模态个数的增加,能量占比逐渐接近1,前12 阶模态的能量占比已超过99.99%,故取前12 阶模态构造Re=3500 时的低维方程,取初值为第一个快照的模态系数,对低维方程数值积分,得到模态系数随时间的变化,并将其与原始快照数据直接在模态上投影得到的系数作对比.

如图2(a),未做修正时,随着时间的推进,低维模型得到的第一模态系数振荡的振幅和频率与DNS数据的误差逐渐增加.而用内在稳定性方法修正后的低维模型,同样取初值为第一个快照的模态系数,进行数值积分,计算的结果与直接数值模拟的结果几乎没有差别(图2(b)).

图2 DNS 与低维模型得到的第一模态系数的时间序列对比Fig.2 The comparison of time evolution of first eigenmode coefficient obtained by DNS and low-order model

下面利用修正低维模型进行参数外推,计算其他Re数 (Re=3400,3300,3200,3100)下的解,并与DNS 计算结果对比(图3).

图3 液层中心点温度振荡时间序列对比Fig.3 The comparison of time evolution of the monitor point at the center of the liquid layer

可以看到,当Re数在3500 附近时,低维模型与DNS 的结果比较吻合,当Re数逐渐远离3500,低维模型得到的振荡的振幅和频率与DNS 结果的误差逐渐变大.所以,上述方法构建的低维模型在一定参数范围内可以反映原系统的定性和定量特点.

为了实现更大范围的参数外推,考虑扩大选取的快照数据的参数范围,即分别取Re=2000,3500,5000 下的201 个流场和温度场数据,无量纲时间间隔为0.01,拼接成更大的快照矩阵(共603 列),对拼接后的快照矩阵取特征模态,构建低维方程,这样可以让特征模态包含更大参数范围内的流动特性.简便起见,后文中将这一组合的情况记为Re=2000,3500,5000.

在此情况下,前20 阶模态的能量占比已超过99.99%,故取模态数为20,对低维方程分别取Re=2500,3000,4000,4500 进行计算,结果如图4 和表4.

表4 低维方程得到的温度振荡频率与DNS 结果对比(Vr=1.00)Table 4 The comparison of temperature oscillation frequency obtained by DNS and low-order model

图4 不同Re 数下由DNS 和低维模型计算出的液层中心点温度振荡时间序列、频谱的对比 (Vr=1.00)Fig.4 The comparison of time evolution and frequency spectrum of temperature oscillation at the center of the liquid layer obtained by DNS and low-order model for various Re (Vr=1.00)

Re=2500,3000 时,由低维方程计算出的温度振幅略小于DNS 得到的温度振幅,而当Re=4000,4500 时,由低维方程计算出的温度振幅略大于DNS 得到的温度振幅.在上述四个Re处,由低维方程计算出的振荡频率与DNS 得到的振荡频率有相似的分布,频率相对误差均在5%左右,说明低维方程可以很好地反映原系统的主要振荡特征.注意到,Re=4500 时,振荡频率的相对误差超过了5%,并且低维方程得到的频谱图中最高峰对应的频率与DNS 相差较大.事实上,由表4 还可以发现,当Re=3000,4000 时,频率误差较小,而当Re接近Rec1和Rec2两个临界值时,误差增大.这个现象可能是因为快照矩阵是Re=2000,3500,5000 下数据的拼接,Re=3500 时的振幅大于Re=2000,Re=5000 的,而特征模态是根据能量排序,这就导致Re=3500 的流动在特征模态中占主导,从而在Re=3500 附近,低维方程的预测效果更好.上述分析表明,取快照矩阵为多个参数下数据的组合,可以扩大低维模型参数外推的范围.

2.2.2 在低维模型上计算分岔

POD-Galerkin 方法降低了原系统的维数,显著减少了数值分岔方法的计算量.对于Vr=0.95,1.00,1.05 三个模型,分别构建了POD 低维方程,其中模态数取为使得前n阶模态能量占比大于99.99%的最小n,并利用低维方程进行数值分岔的计算,得到如图5 所示的分岔图,分支的起点均为Re=1000 下的平衡点,其中H 表示Hopf 分岔,黑色为平衡点分支曲线,红色为周期解分支曲线,实线表示稳定解,虚线表示不稳定解,纵坐标定义为

图5 各体积比下低维方程的分岔图Fig.5 Bifurcation diagram of reduced-order model under different volume ratios

其中bi(i=1,2,···,M) 为模态系数.周期解的norm取为一个周期内norm的时间平均.

对Vr=0.95,分别取Re=2500,4500,6500 下的201 个DNS 得到的速度场和温度场数据,组合成快照矩阵(603 列),模态数为24.对Vr=1.00,分别取Re=2000,3500,5000 下的201 个DNS 得到的速度场和温度场数据,组合成快照矩阵,模态数为20.对Vr=1.05,分别取Re=1800,2500,3500 下的201 个DNS 得到的速度场和温度场数据,组合成快照矩阵,模态数为20.

低维模型的霍普夫分岔点,即为起振的临界值,与DNS 得到的临界值对比见表5.

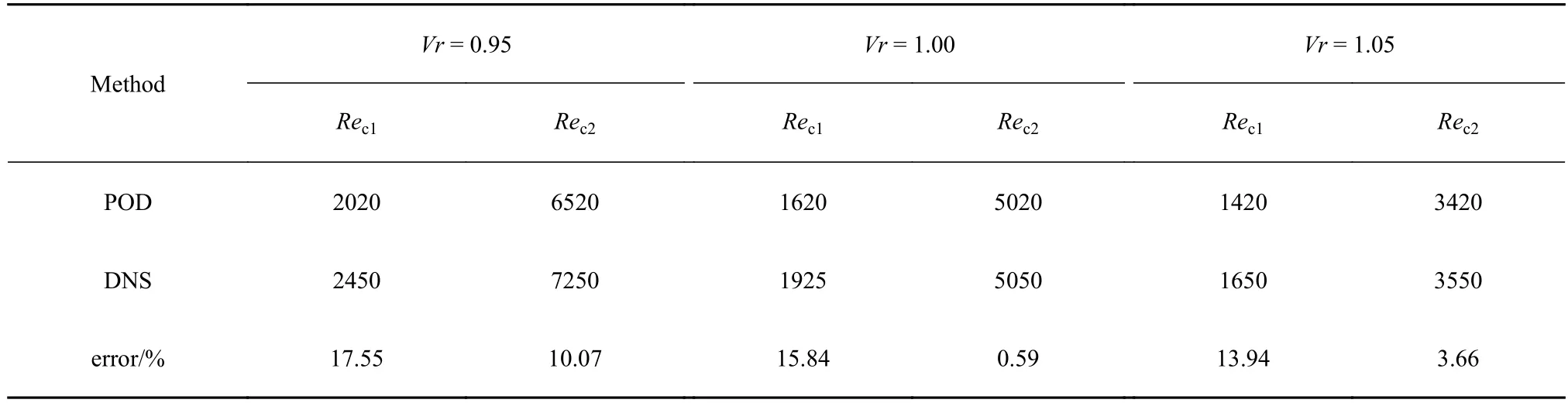
表5 利用低维方程与DNS 计算的临界Re 对比Table 5 The comparison of the critical Reynolds number obtained by DNS and reduced-order model

为了验证低维方程所求周期解的准确性,以Vr=1.00 为例,将不同Re下周期解的频率与DNS 的结果进行对比(表6),可以看到,低维方程上计算得到的周期解频率与DNS 的结果十分接近.

表6 低维方程周期解频率与DNS 结果对比(Vr=1.00)Table 6 The comparison of the frequency of the periodic solution obtained by DNS and reduced-order model (Vr=1.00)

利用低维方程计算出的分岔图,在分支计算和分岔类型上,与原系统一致,临界Re的误差在15%左右,周期解分支的频率与原系统振荡解的频率较为吻合,说明低维模型可以在一定程度上反映原系统解随参数变化的转捩过程.更重要的是,由于流动的控制方程是偏微分方程,离散后的维数通常极高,这使得在原系统上进行数值分岔的计算十分困难,而利用低维模型计算分岔,在牺牲一定精度的前提下,极大地提高了计算效率,低维方程的分岔图可以为确定流动的转捩形式提供初步的指导.

2.2.3 对体积比参数外推

体积比是液池热毛细对流分岔过程的一个重要临界参数,下面考虑利用POD 低维方程,对体积比参数Vr外推.

用Vr=1.00 时Re=2000,3500,5000 情况下的特征模态,作为Vr=0.95,1.05 的特征模态,对Vr=0.95,1.05 分别构建低维方程,发现在一定的体积比和Re范围内,低维方程有较好的外推能力,基本反映了流动的主要特征(图6～图7).

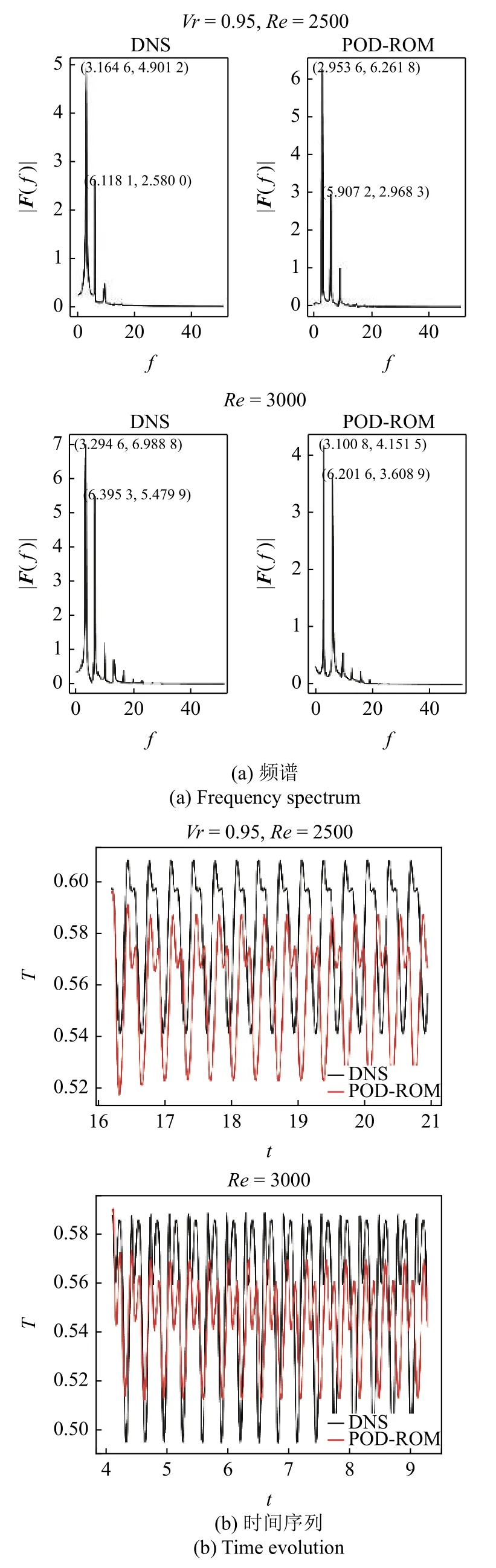
图6 体积比为0.95 时不同Re 下由DNS 和低维模型计算出的液层中心点温度振荡时间序列、频谱的对比Fig.6 The comparison of time evolution and frequency spectrum of temperature oscillation at the center of the liquid layer obtained by DNS and low-order model for various Re numbers under Vr=0.95

图7 体积比为1.05 时不同Re 下由DNS 和低维模型计算出的液层中心点温度振荡时间序列、频谱的对比Fig.7 The comparison of time evolution and frequency spectrum of temperature oscillation at the center of the liquid layer obtained by DNS and low-order model for various Re numbers under Vr=1.05

3 结论

作为流动与传热耦合的非线性过程,热毛细对流有复杂的转捩过程.本文尝试通过直接数值模拟、POD 降维、数值分岔方法相结合的手段,高效分析热毛细对流的转捩.本文构建了贴体坐标系下热毛细对流的POD-Galerkin 低维修正模型,将低维方程的计算结果与直接数值模拟的结果进行对比,得出以下结论.

(1) POD-Galerkin 降维方法可以极大地减少所研究系统的维数,流体力学的控制方程是一组偏微分方程,理论上是无穷维的,用传统的数值方法离散后,维数通常也非常大,对于本文中二维的矩形液层,网格数为1200,有四个未知量u,v,p,T,如果耦合起来求解,维数为4800,通过POD-Galerkin 降维方法,截取大约20 个主要模态,将速度与温度耦合考虑,最后需要求解的常微分方程的维数约为20.

(2) 对于热毛细对流这一速度和温度耦合的模型,POD-Galerkin 降维方法构建出的低维方程,可以反映原系统的流动特性.进一步地,利用内在稳定性修正方法对模型进行修正,可以提高模型的准确性;用不同参数下的直接数值模拟数据拼接成快照矩阵的混合方法可以提高低维方程参数外推的鲁棒性.对于贴体坐标系下的几何参数,低维方程也在一定参数范围内有外推能力,可以对不同物理域内的流动进行快速计算.

(3) 数值分岔方法应用于低维方程,可以得到与原系统相似的分岔行为,计算出的周期解振荡频率与DNS 计算出的振荡频率相对误差在5%以内,说明了在低维模型上用数值分岔方法来分析原系统流动转捩过程的可行性.

后续可能的改进及进一步工作如下:

(1) 本文中的低维模型从定量角度仍有较大误差,鲁棒性也仍有提高空间;

(2) 本文只是二维液层模型,后续还可以推广为拥有更复杂几何形状,更丰富转捩过程的三维模型;

(3) 本文所分析工况的转捩过程较为简单,PODGalerkin 方法是否可以还原更复杂的转捩过程,准确计算转捩点,得到跨越转捩点前后流动的变化特性,仍有待探究.