基于涡量矩理论的绕振荡水翼涡动力学分析1)

郝会云 * 刘韵晴 * 魏海鹏 张孟杰 ** 黄 彪 *,

* (北京理工大学机械与车辆学院,北京 100081)

† (北京宇航系统工程研究所,北京 100076)

** (中国北方车辆研究所,北京 100072)

引言

动边界绕流问题广泛存在于船舶推进[1-3]、水力发电[4]、海洋工程[5-6]等和国家安全以及国民经济相关的重要工程领域.振荡水翼作为轴流泵、水轮机等旋转水力机械中的重要基础研究单元,绕其复杂流场结构对水力机械的动力特性有重要影响[7-9].

研究发现绕动态边界的流场常常存在流态转捩、流动分离、失速旋涡演化等复杂流动行为.早在20 世纪90 年代,文献[10]便通过实验测量了一振荡NACA0012 机翼表面的压力分布与涡通量,成功证实了机翼吸力面上动态失速涡的出现、发展与分离过程.根据旋涡出现的不同位置分别定义有前缘涡(LEV)、尾缘涡(TEV)等.以沉浮翼型为研究对象,Ellington 等[11]发现昆虫和鸟类扇动翅膀时瞬间的高升力归因于机翼前缘涡的增长.Kissing 等[12]对做俯仰和沉浮组合运动的平板前缘涡的形成和分离行为进行了深入研究,发现到达一定攻角时,二次涡会切断前缘涡从剪切层积累环量的路径,随后前缘涡向下对流并与平板分离.文献[13]采用欧拉法与拉格朗日拟序结构方法深入分析了绕二维俯仰振荡翼型的流场演化特征,发现前缘涡诱导较低吸力面上回流从而导致尾缘涡生成.

随着大量研究深入,人们发现流场演化、旋涡发展与物体的水动力特性存在显著的关联.流动分离和动态涡脱落常常导致泵/水轮机在失速状态下运行,对应时刻流场结构及水动力特性极其复杂,常伴有强烈的振动[14-15].文献[16]采用实验和数值方法研究了绕振荡Clark-Y 水翼的空化流动结构和水动力特性,发现逆时针尾缘涡的形成会导致升力下降,而二次涡(SV)的形成导致水动力载荷的波动.Alam 和Muhammad[17]通过理论分析与数值计算,阐明了振荡水翼周围流动结构的演变与产生推/阻力的关系.Xia 和Mohseni[18]通过对比二维振荡平板的旋涡发展与气动升力,发现前缘涡的缓慢对流产生的负升力较小,而尾缘涡的快速脱落产生的正升力较大.这两种升力贡献之间的差异导致了一个持续约两个弦长行程的正升力.Tang 等[19]实验测量了绕NACA66 的水动力特性,发现水翼的低频振荡是由前缘分离涡沿流向覆盖水翼吸力面的长短切换引起的.

在上述研究的基础上,为了深入了解涡动力学对水动力特性的影响,亟需建立旋涡结构与水动力的定量表征关系.相关研究者对此探索提出了许多著名的理论,如K-J 定理[20-22]、普朗特升力线理论[23]等,然而在实际应用中,这些理论均有一定局限性[24],只能用于稳态流场,无法捕捉流动分离、旋涡、激波等现象.对于在不可压缩流体中,作任意运动或变形的物体,文献[25]提出了“涡量矩理论”,揭示了其所受的力和力矩只取决于涡量场的一阶及二阶矩的变化率,该理论能够适用于非定常流,但必须求解物体运动产生的整个涡量场(包括启动涡),除简单近似外,不能用于有涡量逸出的有限区域.在“涡量矩理论”的启发下,又陆续发展了其他用涡量表述的流体动力学理论,例如边界涡量流理论,只需通过物面上动力学量的分布即可求解物体水动力,得到广泛应用[26-28],其中孙茂[29]基于边界涡量流理论解释了昆虫飞行的物理机制.然而边界涡量流理论尚不能清晰地揭示流体内部影响空气/水动力的流动结构.其中文献[24]应用导数矩变化手段发展得到有限域涡量矩理论,获得了在任意有限域流体中自由运动物体所受合力的表达式.该公式通过分别选取物面和无穷远处作为有限域外边界,能够复现上述边界涡量流理论与涡量矩理论,同时解决了涡量矩理论只能适用于无限域的弊端.文献[30]后续将该理论推广至高雷诺数非定常流计算,并证实了理论的普适性.

基于以上调研,尽管针对振荡水翼旋涡演化与水动力特性的研究很多,但是目前尚未有针对水翼局部旋涡结构与其动力特性的综合量化分析.因此,本工作采用数值模拟方法以及有限域涡量矩理论,结合实验数据,研究了俯仰振荡NACA66 水翼的涡动力学特性及其动力响应规律,以期为更好地控制水力机械的动力特性或高效利用水翼运动提供参考数据.

1 研究方法

1.1 控制方程与数值方法

在基于N-S 方程的计算框架内,采用标准k-ωSST 湍流模型[15].其基本控制方程如下:

质量守恒方程

动量守恒方程

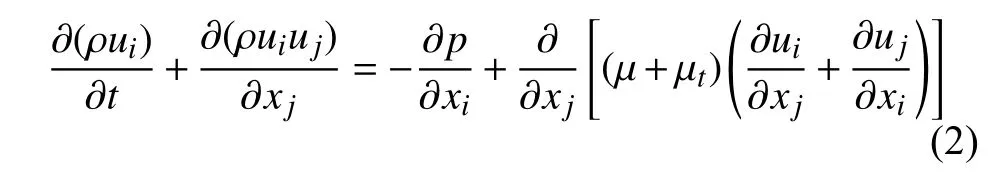
式中,下标i和j分别代表坐标方向,u和p分别为速度和压力,μt为湍流黏性系数,ρ为密度.

由Menter 提出的k-ωSST 湍流模型如下

其中,Pk和Pω为湍流生成项,Dk为湍流耗散项,F1和F2为混合函数,S为剪应力张量的常数项.

计算模型的计算域尺寸、水翼的相对位置以及边界条件设置均与Ducoin[31]在法国海洋工程研究中心(Research Institute of French Naval Academy)的空化水洞中所完成的实验保持一致,以实现后续对比.如图1 所示,边界分别设置为速度入口和压力出口,入口速度5 m/s,水翼表面采用绝热、无滑移的固壁条件.计算域主要包括静态外域和动态内域两部分,其中矩形静态域的长度为16c,高度为1.28c,圆形动态域的直径为1.1c.静态域和动态域之间的数据交互由CFX 表达式语言(CEL)控制,并通过设置动态域的振荡运动来模拟NACA66 水翼的振荡运动.振荡速度为6°/s,振荡幅度为15°,单个周期内振荡轨迹为0°→15°→0°,定义水翼逆时针向上旋转过程攻角为α+,水翼顺时针向下旋转过程攻角为α-.用以对比的实验数据为测得的对应静态固定攻角下水翼的升力系数.

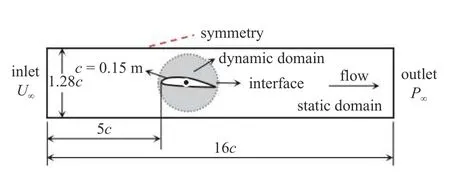
图1 计算域与边界条件设置Fig.1 Computational domain and boundary conditions

图2 给出了计算域网格划分情况,在计算网格中使用了结构化网格策略,对水翼近壁区域网格,尤其是水翼前缘(LE)、尾缘(TE)和尾迹区域进行加密,在边界层设置了500 个节点,使其满足y+=yuτ/ν≈ 1.

图2 水翼周围网格划分示意图Fig.2 Computational grids around the hydrofoil

1.2 基于有限域涡量矩理论的合力计算方法

在任意有限域流体中自由运动物体所受合力的具体表达如下[30]

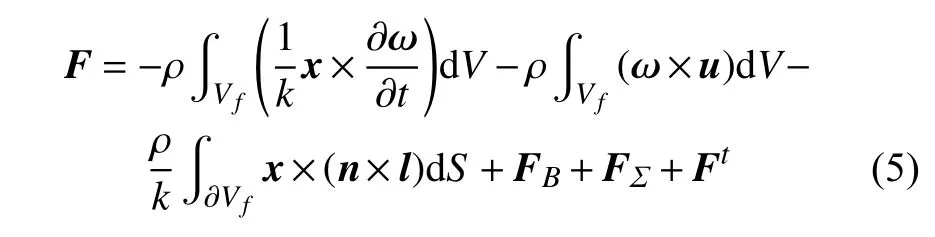
上述表达式中,Vf是以任意控制面 Σ 为外边界和物面∂B为内边界的流体区域,各瞬时变量均为RANS 模型下直接得到的均化结果,每一项都有明确的物理意义.

式(5)右侧第1 项为由翼型运动的非定常惯性效应引起的局部流体涡量变化;第2 项为Lamb矢量或涡力项;第3 项为Lamb 矢量在有限域外边界处的线积分,能够捕捉有限域外脱落旋涡结构对水动力的影响;第4 和第5 项分别为物体运动和变形对水动力的作用以及有限域外边界上的黏性作用.

其中Lamb 矢量积分项代表一个非线性水动力,需要速度u和涡量ω共存,而力的方向总和二者垂直,所以不做功.在局部意义下,这种力正是升力的特点;FB取决于物体自身的运动,而与流动无关,可视为流场的驱动机制;Ft是时均计算模型下的湍流附加项,不影响总合力计算,可忽略该项的求解.对于二维运动模型,上述表达式中n=2,k=1,ρ和μ=ρν分别为流体的密度和黏度,此时物体所受阻力D即为公式各矢量积分项的X方向分量之和Fx,所受升力L为公式各矢量积分项的Y方向分量之和Fy.以Lamb 矢量为例,其阻力方向和升力方向分量分别记作lx和ly.

其中,U∞为无穷远来流速度,c为水翼弦长,s为水翼翼展长度.

2 结果与讨论

2.1 基于Lamb 积分项升力计算分析

流场中的复杂旋涡可由涡量场与流线捕捉.对于二维流场只存在垂直于流动平面方向的涡量,其定义为

为分析绕振荡NACA66 水翼非定常旋涡结构对其水动力产生的影响,采用基于有限域涡量矩理论的合力计算公式建立局部旋涡与升力的联系.有限域设置为能够包括边界层区域的矩形域,同时为了观察翼面上方的旋涡演化行为,矩形下游边界需要超过水翼尾缘.图3 中 Σ1,Σ2,Σ3为三个任意矩形有限域外边界,各域右边界距离水翼尾缘距离分别为ΔX1=0.5c,ΔX2=1.5c,ΔX3=4.17c.图4 对式(5)在不同域下的计算能力进行了准确性验证,已知CFX流体计算软件中采取的内置升阻力计算原理为经典的物面积分

图3 绕振荡NACA66 水翼有限域示意图Fig.3 Diagram of finite domains around the pitching NACA66 hydrofoil

图4 不同有限域升、阻力系数的计算值Fig.4 Predicted lift/drag coefficient in different finite domains

通过与CFD 输出结果对比,有效验证了式(5)在应用中的有效性,同时说明该公式对升阻力的计算与有限域的选取无关.这是由于有限域外的脱落尾涡对物体受力的影响主要体现在流动的非定常性上,如诱导水翼附近涡层的波动等.

图5 展示了式(5)各分项对升力的影响.图5(a)给出了数值计算直接得到的升力系数随水翼转角的变化趋势,以及采用式(5)计算的结果,并与同样来流速度、雷诺数、静态固定攻角下Ducoin[31]在实验中获取的NACA66 水翼的升力系数进行了对比.可见,采用该公式所得到的Cl曲线在幅值和相位上与CFD 计算结果、实验测量数据均吻合较好,为下文基于算例流场预测的准确性开展定量分析奠定基础.在图5(b)中,Lamb 矢量积分项对升力的贡献最大,几乎起全部作用,且与CFD 直接结果基本吻合;涡冲量变化项和边界涡量切割项与涡的脱落、对流行为有关,在动态失速阶段由于旋涡不断生成并向下游对流穿过有限域外边界,两项存在较小幅值的波动,其余时间贡献近似为零;在图5(c)中,由于低速振荡且频率较低,刚体运动项和外边界黏性作用项提供的升力系数量级极小,对总升力的贡献可以忽略.

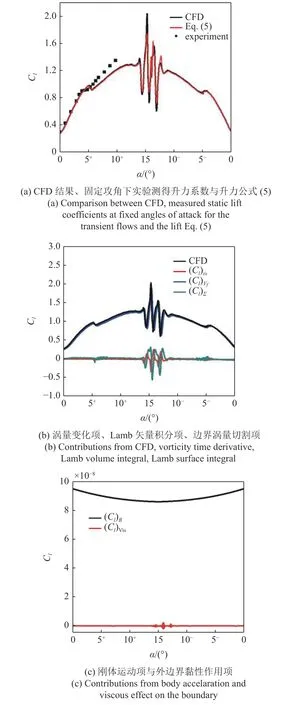
图5 升力公式 (5)的分解Fig.5 Decompositon of lift Eq.(5)

综上可认为Lamb 矢量积分项在升力中占据绝对主导地位,下文将采用这一项来探究局部流动结构对升力的贡献情况.

图6 对比了不同积分域下Lamb 矢量积分项的计算值与CFD 结果,随着积分域的增加,Lamb 矢量积分项计算得到的升力系数曲线较CFD 曲线向右偏离更多,即轻微延迟.为保证能够充分全面地观察到水翼表面上的旋涡发展,同时兼顾计算的准确性,选择右侧边界距离水翼尾缘0.5 倍弦长的矩形域作为积分域,即上述 Σ1所围绕的域,开展下面的工作.

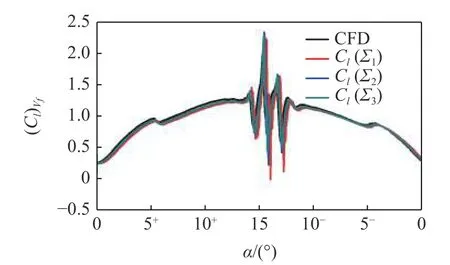
图6 不同有限域下Lamb 矢量积分项的升力计算能力Fig.6 Predictive ability of the Lamb vector integral in different finite domains

2.2 旋涡动力学特性定量分析

为深入分析旋涡结构与动力特征之间的相互作用,结合流场速度流线与涡量分布云图以及上述升力演化曲线,在图7 中将水翼振荡的整个周期分为三个阶段:线性增加段stage I (α+=0°～ 14°)、失速波动段stage II (α+=14°～ 12°)和线性减小段stage III(α-=12°～ 0°).

图7 流场阶段划分Fig.7 Stage division

在线性增加段有以下几个特征阶段.

(1)α+=0°～ 4°:在该阶段中,水翼的升力系数随着攻角的增大呈线性增长的趋势.此时绕振荡水翼流场呈现准层流状态,如图8(a)所示.

(2)α+=4°～ 6°:升力系数在该阶段有一明显的拐点.这是因为绕水翼前缘流场出现了层流向湍流的过渡转捩(laminar separation bubble,LSB).如图8(b)所示,当α2=4.08°时,水翼前缘处无层流分离现象产生,在水翼尾缘X/C=0.7 位置处,由于逆压梯度的作用,形成LSB 区域.如图8(c),当水翼旋转到α3+=5.4°时,层流向湍流的过渡转捩区域逐渐转移至水翼前缘位置,这一过程导致升力曲线出现拐点.

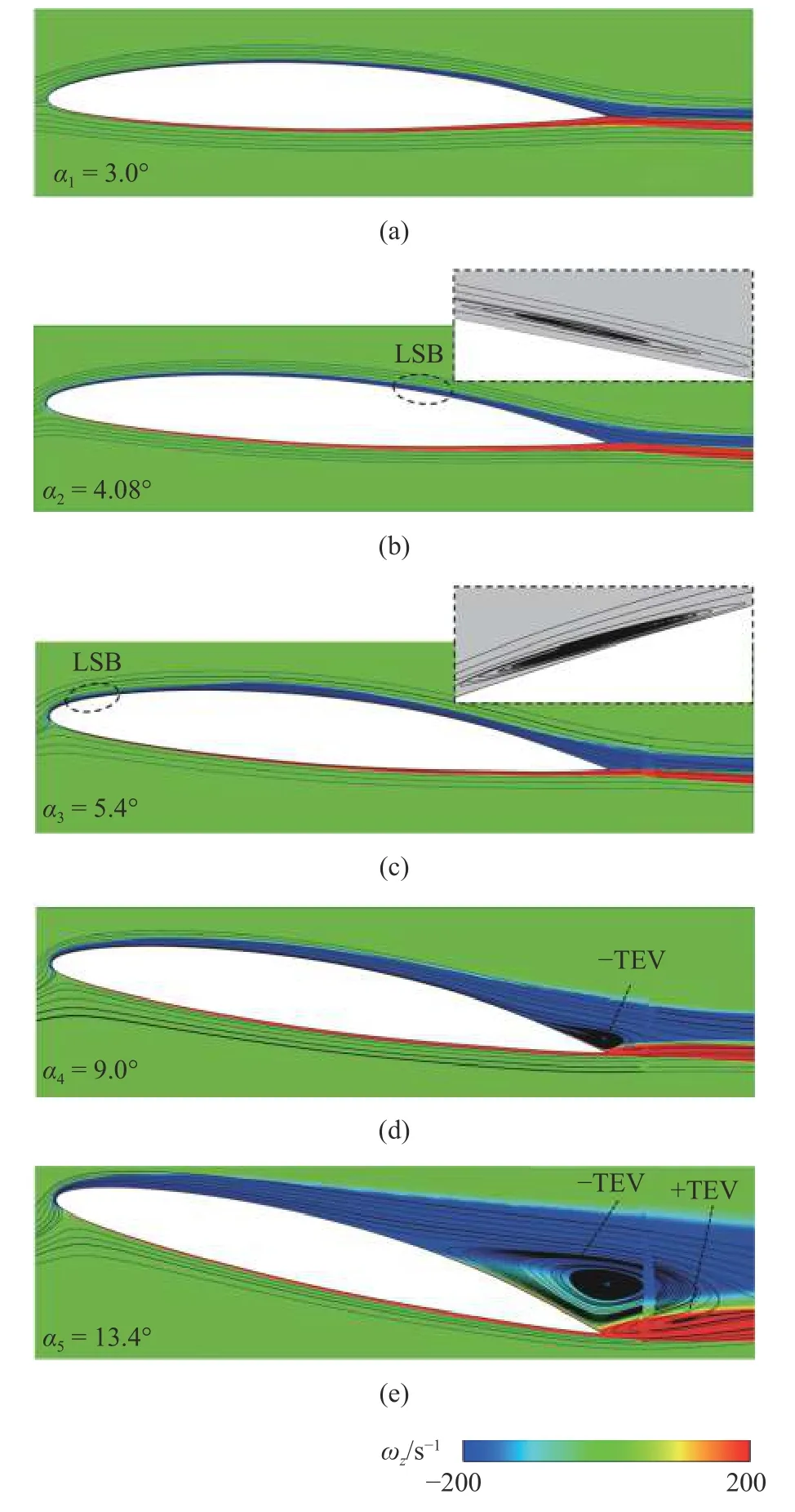
图8 线性增加段典型时刻流场Fig.8 Typical flow fields in linear increasing stage

(3)α+=6°～ 14°:升力系数在此阶段不断增大.在水翼吸力面上,出现一顺时针的尾缘涡-TEV,如图8(d)所示;在水翼向上旋转的过程中,-TEV 逐渐增大,并向水翼前缘发展;α5+=13.4°时,如图8(e)所示,在水翼尾缘的吸力面上,-TEV 的下游出现一逆时针的尾缘涡 +TEV.

图9 给出了水翼在向上振荡过程中,分离点及再附着位置随转角的变化趋势,其位置根据Prandtl流动分离判据给定 (∂ux/∂y)y=0=0.从图中可以看出,绕振荡水翼流场呈现准层流状态时,层流分离点位于水翼尾缘X/C=0.6～ 0.7 之间,并随攻角增加缓慢前移;当水翼攻角位于α+=4°～ 6°时,层流分离点由水翼尾缘迅速移动至前缘,并在靠近前缘顶点处发生层流向湍流的过渡转捩;此后全局流场转变为湍流流动,特别是当进入动态失速阶段时,流场中的大尺度分离涡不断生成、相互作用并对流脱落,而分离点始终位于接近水翼顶点位置.

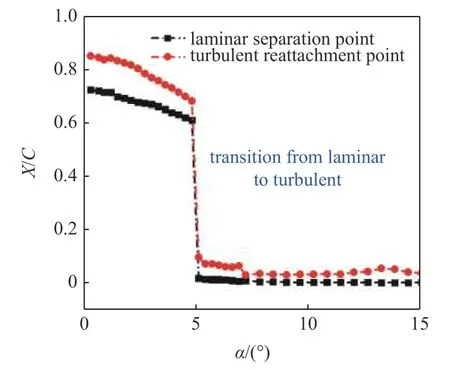
图9 分离点及再附着位置随攻角的变化情况Fig.9 Evolution of separation points and reattachment positions with the angle of attack

在失速波动段(α+=14°～α-=12°),升力系数曲线存在三次升力峰值,对应着三次周期性的旋涡发展与脱落,每个周期内存在相似的旋涡演化行为,波动峰值分别位于α+=13.92°,α-=14.73°,α-=13.51°,现以旋涡发展的第二个周期为例,如图10 所示,研究流场结构演化与水动力特征.

图10 失速波动段典型时刻流场Fig.10 Typical flow fields in dynamic stall stage

(1)α+=14.76°～α-=14.73°:该阶段水翼升力系数处于上升阶段,水翼吸力面在-TEV 和 +TEV 的基础上诱导形成一个顺时针前缘涡-LEV,如图10(a)所示,此时绕振荡水翼同时存在三个旋涡,随后,-LEV 和-TEV 同时向水翼中央移动,直至攻角α10=14.73°时融合形成一个新的-LEV,几乎覆盖水翼整个吸力面,如图10(b)所示,此时升力系数达到局部峰值.

(2)α-=14.73°～ 14.32°:升力系数随攻角减小呈近似线性下降趋势.这个过程中,-LEV 向水翼尾缘快速移动,并与 +TEV 相互作用直至二者完全脱落.如图10(c)所示,此时-LEV 即将完全脱离翼面,升力达到局部最小值.

由此推断-LEV 的充分发展以及-LEV 与+TEV的相互作用脱落是导致升力系数曲线波动的重要影响因素.

线性减小段与线性增加段的流场变化规律相似.

(1)α-=12°～ 5°:该阶段升力系数随攻角减小而线性减小,最初在水翼尾缘同时存在-TEV 和 +TEV,如图11(a),随后-TEV 和 +TEV 相互作用,+TEV 脱落,如图11(b)所示,水翼吸力面仅剩下-TEV.

图11 线性减小段典型时刻流场Fig.11 Typical flow fields in linear decreasing stage

(2)α-=5°～ 4 °:该阶段流场行为近似于线性增加段,绕振荡水翼的层流分离点由水翼前缘向尾缘移动,导致升力曲线出现拐点.

(3)α-=4°～ 0°:升力系数随攻角减小线性下降,如图11(c),绕振荡水翼流场由湍流再度转变为层流.

由上述分析可知,绕振荡NACA66 水翼流场中存在着复杂的非定常旋涡,尤其是在动态失速阶段,旋涡演化呈现出与升力的强关联性,从流场观测上来看,振荡水翼获得高升力的机制是前缘涡不断发展并附着在水翼吸力面上,翼后缘的涡层不断地脱泻到尾流中去,但是其中的定量关系尚不明确.下面通过对不同旋涡内ly积分来计算其对瞬时升力的贡献情况.

如图12 所示黄色封闭虚线为典型时刻下,基于涡量与流线所识别的各个旋涡结构积分域.

图12 典型时刻局部旋涡结构积分域示意图Fig.12 Diagram of vortices’ domain of integration at a typical moment

图13 展示了动态失速阶段九个特征时刻的旋涡贡献情况.可以看到,在升力抵达峰值之前的上升段,存在典型的三涡流场,结合图10(a),此时-LEV与-TEV 同时向水翼中央移动,+TEV 附着在水翼尾缘.这个过程中-LEV 和-TEV 提供了部分正升力.在α6,α9,α12三个时刻中,-LEV 对总升力的贡献分别为17%,9%,17%,-TEV 对总升力的贡献为29%,10%,12%,而+TEV 提供了近似为零的极小负升力;在α7,α10,α11三个时刻,瞬时升力达到局部峰值,如图10(b),-LEV 几乎覆盖整个水翼吸力面,其对瞬时升力贡献分别为50%,37%,37%;在α12,α13,α14时刻,瞬时升力达到局部最低值,此时-LEV 和+TEV 经过相互作用即将或者完全脱离水翼表面,-LEV 的贡献接近于0,+TEV 提供了负升力,分别占瞬时升力的-20%,-22%,-44%.

图13 失速波动段关键旋涡贡献Fig.13 Key vortices’ contributions during the dynamic stall stage

综上所述,附着的-LEV 和-TEV 提供正升力,+TEV 提供负升力;峰值时-LEV 的贡献最大接近50%,当升力达到局部最小值时,-LEV 的贡献约为0,而 +TEV 的负贡献可高达40%.

上文分析了有限域内不同类型旋涡对升力的净贡献情况,然而值得注意的是,旋涡内部不同局部区域所提供的升力有正有负.如图14 所示为ly云图,左侧为全局流场图,右侧为各个旋涡区域的局部放大图.对比图10 发现ly不仅能够精确捕捉到对应的旋涡区域,同时能够直观表达出不同流场结构的升力贡献,红色表示对应的旋涡结构提供了正升力,蓝色表示对应的旋涡结构提供了负升力.且各个旋涡内部均被分割成多个部分,这是由于流场速度的方向改变导致,而具体旋涡的净贡献是区域积分的结果.

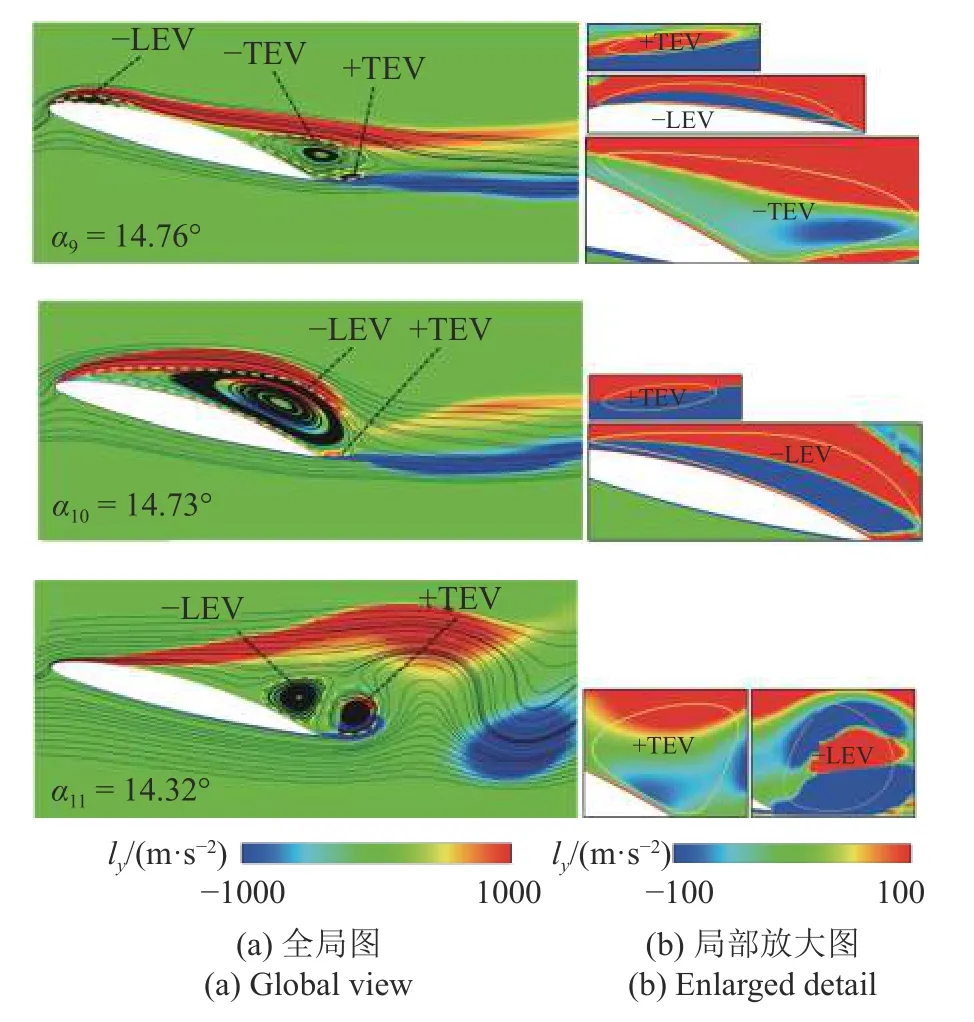
图14 旋涡结构与Lamb 矢量Y 向分量云图Fig.14 Vortices and ly contours

图15 追踪了第二次峰值所对应的旋涡发展脱落周期中,特定-LEV,-TEV,+TEV 对瞬时升力的贡献大小与演化情况.可以看到,各旋涡所提供的升力与其对瞬时升力的贡献率保持同步,当融合后的-LEVly积分值达到最大值时,它对瞬时升力的贡献也最大,接近50%;在发展过程中,+TEV 始终提供负升力,-LEV 与-TEV 在融合之前提供正升力,融合后新-LEV 继续向下对流,与 +TEV 相互作用脱离水翼表面的过程中,在α-=14.56°时产生短暂的负升力,而这期间+TEV 的负贡献较大,在α-=14.56°时高于40%.因此失速行为发生时可认为是+TEV 通过诱导有利-LEV 的脱落及自身贡献负升力两种途径从而使升力快速下降.

图15 一个失速周期内的旋涡升力贡献演化Fig.15 Contributions of vortices during one stall period

为了进一步探究上述旋涡逸出有限域后将如何影响水翼的动力特性,图16 给出了在失速阶段典型时刻尾流涡分布,包括涡量场和ly云图.可以看到顺时针尾流涡各区域均提供正升力,而逆时针涡各区域均提供负升力.

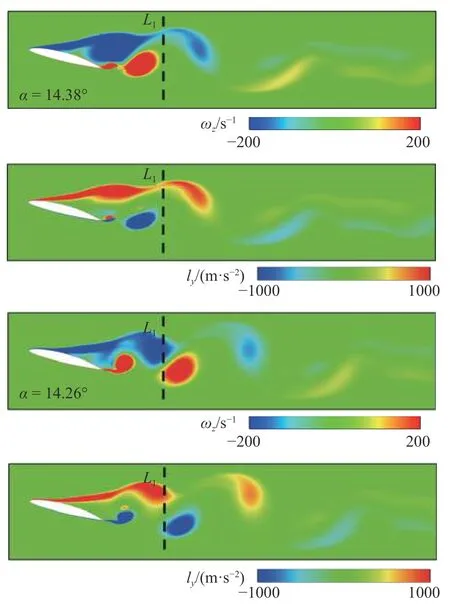
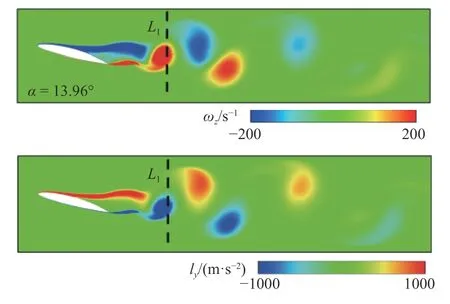
图16 尾流旋涡结构与Lamb 矢量Y 向分量云图Fig.16 Wake vortices and ly contours

结合图5 中边界涡量切割项可准确捕捉域外旋涡的贡献,在α-=14.38°时,域外尾涡提供了负升力,随后脱落的顺时针旋涡(提供正升力)与脱落的逆时针旋涡(提供负升力)不断逸出有限域而进入域外尾涡区域,由于不断逸出的逆时针旋涡“携带”更高的正升力,大于同一时刻进入域外的顺时针涡所提供的负升力,因此域外尾涡对升力的贡献逐渐上升.在α-=13.96°时,尾涡整体提供了正升力.但总体来看,域外尾涡对升力的贡献较小,仅在失速阶段,域外尾涡提供的升力发生小幅波动,体现了流动的非定常性.

3 结论

(1) 绕振荡NACA66 水翼流场存在边界层转捩、流动分离和动态涡失速等行为,随着水翼攻角的增加,绕水翼的层流向湍流转捩点由尾缘移至前缘发生,随后在水翼尾缘吸力面上出现顺时针尾缘涡-TEV,-TEV 不断增大并向前缘发展,与水翼前缘生成的顺时针旋涡-LEV 融合形成覆盖水翼整个吸力面的-LEV,此后与尾缘吸力面逆时针旋涡+TEV 相互作用直至完全脱落分离.在水翼向下旋转阶段,水翼近壁面流动逐渐由湍流转变为层流.水翼振荡过程中,前缘涡与尾缘涡的相互作用引起前缘涡完全脱落分离,直接导致了动力失速现象的发生.

(2)动态失速涡与升力演化密切相关.基于有限域涡量矩理论的升力公式由涡量变化项、Lamb 矢量积分项、边界涡量切割项、刚体运动项以及外边界黏性作用项5 项构成,其中Lamb 矢量积分项占主导,能够用来表达振荡水翼升力演化,进而捕捉局部旋涡结构对升力的贡献,并直观展示不同流动结构对升力的作用方向及大小,结果显示附着的-LEV和-TEV 提供正升力,当-LEV 发展覆盖整个吸力面时,其对升力的局部贡献最大且接近50%,+TEV 提供负升力.然而有限域内任一旋涡内部的不同位置提供的升力有正有负;域外脱落尾涡却只提供一种贡献,顺时针涡提供正升力,逆时针涡提供负升力.