双小行星探测轨道动力学研究进展1)

王 悦 伏 韬 张瑞康

(北京航空航天大学宇航学院,北京 102206)

引言

双小行星系统由在万有引力作用下彼此环绕运行的两颗小行星组成,在近地小行星、主带小行星和柯伊伯带小天体中普遍存在.据估算,大约16%的近地小行星和直径小于10 km 的主带小行星是双星系统[1-2].自1993 年“伽利略”探测器发现首个双小行星系统243 Ida 以来,大量双小行星系统被相继发现,引起和推动了行星科学和航天动力学等领域对双小行星系统的关注和研究.

最早引发关注的是双小行星系统的形成和演化理论.目前的主流理论认为,较小的双小行星系统是由“碎石堆叠”的单个小行星在热力学的YORP(Yarkovsky-O'Keefe-Radzievskii-Paddack effect)效应驱动下不断加速旋转,超过临界转速后分裂而形成[3-4],较大的离心力使得小行星表面高纬度地区的物质向赤道积聚,形成了主星顶部锥台形、赤道隆起的典型形状[5-6].分裂后双星系统的动力学演化取决于次星和主星的质量比[7-8].当双星质量比较接近时(质量比≥0.2),双星系统在潮汐力的长期作用下逐步演化为双同步系统,即两颗小行星互相潮汐锁定;当双星质量悬殊时(质量比 ＜ 0.2),系统是非束缚的,可能在混沌的动力学演化中逃逸并形成小行星对(asteroid pair),亦或次星在引力矩作用下加速旋转分裂,并最终演化为稳定的三星或双星系统[9].而拥有较大主星(尺寸＞20 km)的双小行星系统,通常次星尺寸较小且主星转速低于旋转分裂的临界速度,这表明该类双星系统可能形成于大型的碰撞过程[10-11].此外,部分双小行星系统还可能通过主星引力捕获另外一颗小行星,或在接近大天体时被潮汐力撕裂而形成[12-13].

在航天动力学方面,近二十多年来,美国和日本成功实施了多次小行星探测任务,不断掀起小行星探测的热潮.小行星探测对揭示太阳系起源、开展行星防御和推动小行星资源开采利用都具有极为重要的意义.与单小行星相比,双小行星系统具有更高的研究和探测价值:其一,对双小行星系统形成和演化过程的研究可为行星系统的形成和演化提供宝贵线索;其次,旋转分裂形成的双星系统为研究小行星内部物质组成和构造提供了可能;最后,双星相对运动的微小改变更容易被观测,是小行星防御技术验证的绝佳对象.因而,双小行星系统正在成为小行星探测与防御备受关注的新目标.但同时,双小行星系统附近的复杂力学环境为探测器轨道动力学和任务设计带来了全新的挑战,促进了航天动力学在多个方向的进展.

对双小行星系统不规则引力场和双星间相对运动的准确建模是研究探测器轨道动力学问题的基础.针对不规则天体的引力场描述,目前主要形成了三种通用方法:质点群法、球谐函数法和多面体方法,以及一些基于特定简单几何体的近似方法.它们具有各自的优缺点,例如质点群法简单、灵活性高,但不具备边界条件,随精度要求的提高计算量急剧增加;球谐函数法具有解析形式、计算效率高,但靠近天体表面收敛速度慢甚至发散;多面体法精确、完备,但计算量大,不利于解析研究[14];基于特定几何体的方法只适用于具有特定形状特征的天体.因此,通常需要根据具体问题和应用场景选择合适的方法或将不同方法混合使用.

在双星不规则引力的相互作用下,它们的相对运动构成了复杂的姿态轨道耦合的二体问题,被称为完全二体问题(the full two-body problem,F2 BP)[15].这种两个任意刚体构成的二体问题是天体力学中的一个基本问题,得到了广泛的研究[16-19].学者们发现采用相对位置和姿态坐标来描述二体的相对运动,可以降低系统自由度,并有效地简化问题,得到了一般性的系统运动方程[16],而相对运动的具体演变由方程中的相互引力势模型所决定.

双星的相互引力势本质上是将分属两星的两质量元间的万有引力势分别对两个刚体求一次体积分,即是一个双重体积分.除了一些特殊情况,两个任意质量分布刚体之间的相互引力势没有封闭的表达式,通常采用无穷级数展开的方法.以不规则天体引力场的建模方法为基础,发展出了多种相互引力势的建模方法.根据处理双重体积分的数学思路,可以将其分为三种类型:基于简单几何体的模型、基于刚体质量分布参数(如惯性张量/积分、引力场球谐系数等)的模型,以及基于多面体形状和刚体质量分布参数的混合模型.针对一些特殊的简化情况,学者们在球-椭球、椭球-椭球和球-任意形状的双星模型下,得到双星相对运动的一些解析结果,如系统稳定性和双星相对运动的平衡构型及稳定性[8,15,20-22];在更精确的基于质量分布参数模型下,利用数值方法研究了两颗多面体小行星的相对运动[23].研究所揭示的双星相对运动的平衡构型与实际天文观测数据一致,为探测器轨道动力学研究和任务设计奠定了可靠的基础,同时也检验和丰富了行星系统的演化理论.

在不规则引力场建模和双星相对运动问题得到解决之后,就可以在此基础上研究探测器的轨道动力学.双星和探测器构成的三体系统满足限制性假设,因而可将探测器的运动视为一个限制性三体问题(the restricted three-body problem,R3 BP).与球形主天体的经典限制性三体问题相比,由于双星对探测器的非球形引力和双星之间的姿态轨道耦合动力学,该动力学系统呈现出新的丰富的动力学特性,被称为限制性完全三体问题(the restricted full threebody problem,RF3 BP).2005 年,Scheeres 和Bellerose[24]在附加太阳引力的限制性希尔完全三体问题模型下,给出了系统的运动方程,奠定了这类问题研究的基础.接着,学者们在同步椭球-椭球(或球-椭球)的简化模型下,对系统的平动点及其稳定性,周期轨道及其稳定性和基于不变流形的转移轨道等一系列问题开展了深入的研究[25-29].同时,为了更加真实地模拟双星附近的动力学环境,学者们采用了更加精确的多面体-椭球或双多面体模型,或一并考虑太阳光压力和太阳引力摄动,利用数值方法对上述问题进行了研究[30-33].系统存在的多种类型的周期轨道能够满足双星近距离探测的不同任务需求,但双星附近力学环境的不确定性等因素将导致实际的飞行轨道偏离名义轨道,甚至撞击小行星表面.因此,双星系统附近高效的轨道维持是另一项重要的研究内容,目前主要针对轨道维持策略和实现手段展开了研究[34-36].

近年来,学者们认识到太阳光压力在双星系统附近的轨道动力学中也扮演着重要的角色,在精确的任务轨道设计阶段需要加以考虑.研究发现在某些情况下,选择不同的太阳光压力模型可能会导致显著不同的结果[37].另一方面,小行星的弱引力场为太阳帆航天器提供了非常适用的场景.与传统的将太阳光压力视为摄动不同,太阳帆可以利用太阳光压的微小推力产生传统航天器难以实现的平衡点及周期轨道(如悬浮轨道),并可通过调整太阳帆姿态实现轨道的维持和机动.2004 年,McInnes[38]广泛讨论了太阳帆在限制性三体问题中的应用.2018 年,Heiligers 和Scheeres[39]将相关理论推广到了双小行星系统中,验证了悬浮轨道的存在.2019 年Guzzetti 等[36]将太阳帆推进应用于平动点轨道的维持.

上述探测器轨道动力学的研究是在限制性三体问题框架内,重点研究了平动点、周期轨道及其衍生问题,这是对球形主天体的经典限制性三体问题的自然推广.然而事实上,在双小行星附近的轨道动力学中,还存在对更为经典的受摄二体问题的推广,即环绕系统单颗星的轨道动力学.以环绕双小行星系统主星的轨道为例,在靠近主星的区域,主星的中心引力远大于次星的引力和其他摄动力,本质上属于受摄二体问题的范畴,其开普勒轨道要素变化的时间尺度远大于探测器轨道周期.这时如果仍然采用限制性三体问题模型,其积分效率太低,更糟糕的是掩盖了受摄二体问题所蕴含的清晰的轨道演化图景,难以揭示系统固有的演化机制和特性.受摄二体问题是天体力学最为经典的问题,最初被用来研究行星和行星卫星的轨道运动.近几十年来,二体问题的轨道摄动理论在航天动力学,尤其是人造地球卫星轨道动力学领域得到了极大的发展,形成了丰富的研究成果.2020 年,Wang 和Fu[40]进一步将二体问题的轨道摄动理论拓展到双小行星系统中,建立了环绕主星的半解析轨道动力学模型,揭示了环绕主星轨道运动的Lidov-Kozai 机制,分析了轨道长期演化的稳定性[41].

进入21 世纪的第三个十年,对双小行星系统的研究和探测将由理论转为实践.目前已有多个双小行星探测任务被提出和批准:(1)美国和欧洲联合提出了AIDA (asteroid impact and deflection assessment)任务,包括美国DART (double asteroid redirection test)和欧洲Hera 两个探测器,计划以DART 探测器(已于2021 年11 月发射)撞击双小行星系统65803 Didymos 的次星,以Hera 探测器(拟2024 年发射)对双星系统的两个成员进行详细的勘察,并测量DART 探测器的撞击对次星轨道的影响,评估动能撞击在小行星防御中的可行性[42];(2) 2021 年10 月发射的美国Lucy 探测器将首次造访特洛伊小天体,它将于2033 年飞掠最后一个探测目标—位于日木系统L5 点的特洛伊双小行星系统617 Patroclus;(3)美国科罗拉多大学Daniel J.Scheeres 教授担任首席科学家的Janus 探测计划(拟2022 年发射)将对两个近地双小行星系统1996 FG3 和1991 VH 进行飞掠探测[43].

与前述的轨道动力学理论研究不同,面向探测任务的轨道设计还需要进一步考虑实际的任务需求和来自探测器平台的约束条件,目前的研究主要包括两个方面,一是基于不变流形的低能转移和着陆/起飞轨道研究,二是针对特定探测目标和任务需求的力学环境分析和任务轨道设计,例如在DART 任务中为其携带的立方星设计任务轨道,实现对溅射粒子和撞击坑的长时间、近距离观测.

本文的主体结构安排及各部分间的关系如图1所示.第1 节首先论述双星引力势建模与相对运动研究,以不规则天体的引力场模型作为起点,其是双星系统相互引力势建模的基础,而相互引力势又是研究双星相对运动的基础.通过双星相对运动的研究可以确定双星系统自身的运动状态,是探测器轨道动力学研究的前提和基础.探测器在双星系统附近的轨道动力学按照理论框架、求解思路和关注点的不同,主要可分为限制性三体问题和受摄二体问题两类,将在第2 节和第3 节分别对其研究现状进行论述.随后,第4 节将介绍基于探测器轨道动力学研究的理论成果,进一步考虑实际任务需求和约束的轨道动力学分析与设计.

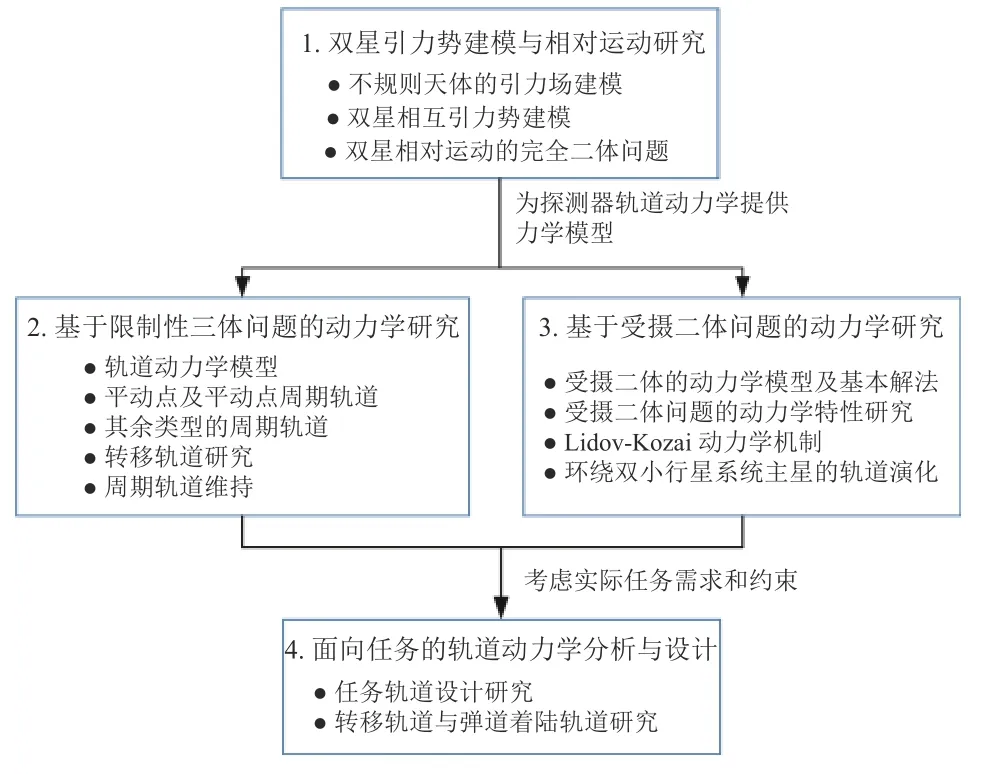
图1 本文结构安排及各部分之间的关系Fig.1 Organization of this paper and connections between different parts

1 双星引力势建模与相对运动研究

1.1 不规则天体的引力场模型

单颗小行星的引力场模型是双星引力势建模的基础.不规则天体引力场的通用建模方法目前主要有三种:质点群法、球谐函数法和多面体方法,此外还有一些基于特定简单几何体的引力场近似方法.

1.1.1 质点群法

质点群法是描述不规则天体引力场的一种直观方法.该方法将小行星表面所覆盖的实体离散成一系列体积元,计算引力时用质点代替体积元,最后对所有体积元求和,以近似描述小行星的引力场.

假设将小天体划分为n个体积元,ri和Mi分别表示第i个体积元的位置和质量,则空间位置为r的单位质量的引力势表达式为

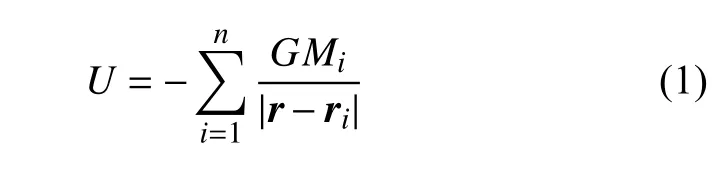
可以看到,质点群法的优势在于算法简单,易于编程实现;容易通过增加体积元的数量来提高引力场建模精度;针对“碎石堆叠”的质量分布不均匀的小天体,可通过调整各体积元的质量权重和离散规则,实现对真实质量分布的模拟,如图2 所示.

图2 质点群法对椭球的不同离散方式[14]Fig.2 The different way of filling the ellipsoid with point masses[14]

质点群法在小行星附近轨道动力学研究中得到了成功的应用.Ren 和Shan[44]利用质点群法研究了小行星的着陆轨迹优化.Yu 等[45]将双星系统(65803)Didymos 中的次星用质点群近似描述,研究了次星受到撞击后溅射物的轨道演化.

质点群法的缺陷也很明显.收敛非常慢,随着对精度要求的提高,所需体积元数量的急剧增加会造成计算量的迅速攀升;其次,离散的体积元数量过多,会造成计算的累计误差较为显著;最后,质点群法无法描述小行星的表面边界[46],也就无法提供直接的碰撞检测条件.

1.1.2 球谐函数法

球谐函数法是描述行星引力场最成熟和经典的方法,在人造地球卫星轨道动力学中具有重要的应用.该方法将引力势表示成由正交球谐函数组成的无穷级数形式.引力势球谐函数展开的一般表达式为

式中,r,φ,λ 为质点在球坐标系下的坐标,即距离,经度和纬度;Plm为连带勒让德函数;re表示参考球半径,可取为天体表面距离质心的最远距离,该参考球又被称为布里渊球;各阶球谐系数Clm和Slm用以描述天体的质量分布.

球谐函数法有着解析的级数表达式,可根据精度需要在任意阶截断,在动力学的解析研究方面具有巨大的优势.应用球谐函数法的关键是获取天体的引力场球谐系数,其主要技术途径是通过天体的外形进行估算或利用轨道飞行数据进行反演计算.

在布里渊球内部,球谐级数将发散,意味着对于形状不规则的小天体,在靠近表面的较大区域内其引力场无法通过球谐函数法描述.

针对球谐函数法收敛域的局限性,Werner[47]首次提出了内球谐函数法.该方法的收敛域为一个球心在天体外部、与天体表面相切的球体,称为内布里渊球,据此可利用球谐级数描述该切点上方区域的引力势.Takahashi 等[48-50]将其成功地应用到小天体表面引力场建模和动力学分析中.结合球谐函数法和内球谐函数法描述小天体表面附近的引力场,具有比下文将要介绍的多面体模型更高的计算效率.Wu 等[51]应用该方法研究了火卫一的表面起飞问题,将起飞轨迹经过的区域分段用内球谐函数法和球谐函数法来描述,如图3 所示.

图3 火卫一复合球谐函数模型分区示意图[51]Fig.3 Regionalization of the compound gravity harmonic approach of Phobos[51]

内球谐函数法表述的场点引力势函数的一般表达式为

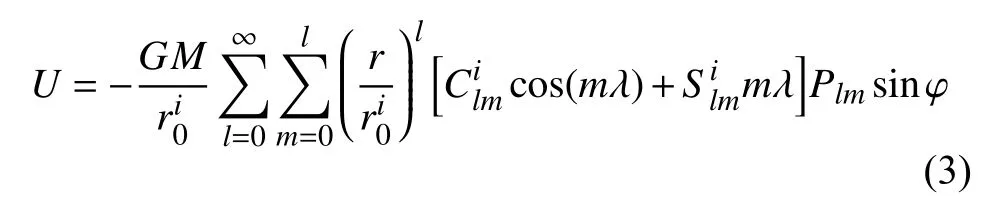
该方法使用的坐标系原点为内布里渊球球心,r,φ 和λ为该坐标系下场点的球坐标;表示参考球半径,一般取为内布里渊球半径;是与天体质量分布相关的球谐系数.

椭球谐函数法是球谐函数法的另一个重要的推广和改进,它将引力势展开为正交椭球谐函数的级数,其收敛域为包含天体的最小椭球,使之更适合描述扁长和不规则形状小天体的引力场.如图4,椭球谐函数法可以极大地拓宽球谐函数法的有效范围,其代价是正交椭球谐函数计算的复杂性.而且,该方法仍然不具有全局收敛性,无法精确计算小天体表面的引力场.另外,与质点群法类似,球谐函数法和椭球谐函数法也无法提供直接的天体表面碰撞检测条件.

图4 小行星4769 Castalia 的球谐(左)和椭球谐(右)引力场模型的收敛域[14]Fig.4 The convergence domain of spherical harmonics (left) and ellipsoidal harmonics (right) gravity models of the asteroid 4769[14]

1.1.3 多面体法

针对球谐函数法的局限性,20 世纪90 年代Werner 等[46,52]提出了利用匀质多面体模型计算不规则小天体的引力势、引力和引力梯度的方法.小行星的多面体模型中,每一个面均为三角形,如图5所示为小行星433 Eros 的多面体模型.

图5 小行星433 Eros 多面体模型Fig.5 The polyhedron model of the asteroid 433 Eros

利用所有三角形顶点、边和面的信息,就可以得到场点引力势的一般表达式

式中,σ 为多面体的密度;re和rf为场点到多面体棱上和面上任意一点的矢量;Ee和Ef是基于二元并矢的与多面体形状相关的常数矩阵;Le和 ωf是描述场点与边、面相对关系的几何量.对引力势分别计算一次和二次梯度,可得到引力和引力梯度的解析表达式(详细的推导和表达式可参考文献[46]).

多面体法可以精确模拟天体不规则的表面形状,建模精度取决于对天体观测数据的精度.此外,多面体法具有封闭的表达式,不存在收敛性和截断误差的问题,能够精确描述小天体表面引力场,因而非常适合小行星着陆和起飞等表面动力学问题的研究.但多面体法的高精度以大量计算为代价,因而在远离小行星表面的区域常切换为球谐函数法以提高计算效率.多面体法的另一个优势在于提供了天体表面碰撞检测的直接指标.

多面体法凭借其对不规则引力场的精确建模能力,被广泛用于小行星附近的轨道动力学研究中,并被成功应用到人类首个小行星环绕探测器NEAR(near Earth asteroid rendezvous).

1.1.4 基于特定简单几何体的近似方法

除了上述三种通用的不规则天体引力场建模方法外,还存在一些基于特定简单几何体的引力场近似方法,适用于具有特定几何形状的天体.例如匀质椭球体模型、链接质点模型和质点连杆模型等.

匀质椭球体的引力势可表示为基于椭圆积分的封闭表达式[53]

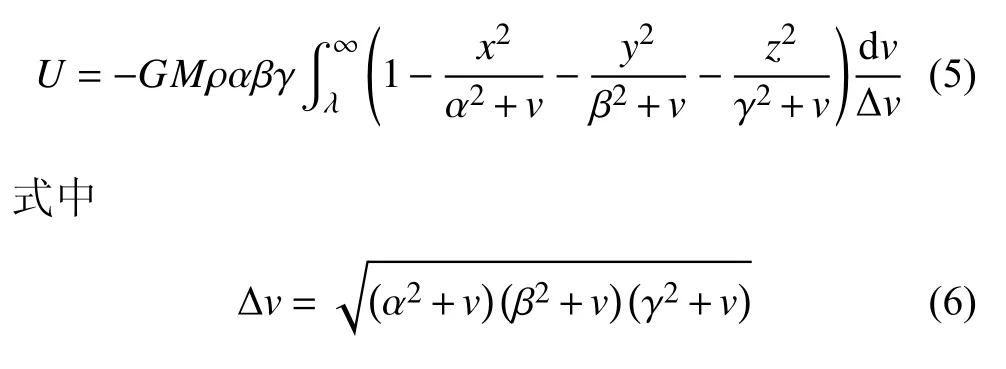
Ms为球体质量; ρ 为椭球密度; α ,β 和 γ 分别表示椭球三轴半径,存在关系 0 ＜γ ≤β ≤α ; λ 满足

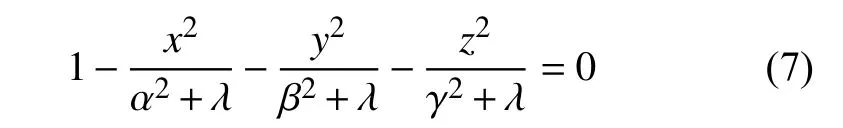
对引力势分别计算一次和二次梯度可得到引力和引力梯度.该模型引力场表达式中涉及的无穷积分可通过卡尔松(Carlson)椭圆积分算法进行快速计算.

链接质点模型由两个或两个以上的质点用无质量的杆元件(质点间相对位置固定) 连接构成.1987 年,Chermnykh[54]首次提出了轴对称刚体的两质点旋转哑铃模型,Kokoriev 和Kirpichnikov[55-56]利用该模型研究了二体的平面运动.该哑铃模型附近的限制性轨道运动可以视为圆型限制性三体问题的推广,因此能够对诸如平动点和稳定性的动力学问题进行解析的研究[57-60].2015 年,Zeng 等[61]利用质点偶极子模型描述形状狭长的小行星,建立了该模型与真实小行星系统参数之间的关系.2017 年,Lan 等[62]利用三质点链接模型建立了拱形外形天体的引力模型.Qian 等[63]利用该模型研究了小行星附近考虑太阳引力的参数共振轨道.两质点和三质点的链接模型如图6 所示.

图6 小行星216 Kleopatra 两质点链接模型(上)与243 Ida 三质点链接模型(下)[62]Fig.6 The double-particle-linkage model of 216 Kleopatra (up) and the triple-particle-linkage model of 243 Ida (down)[62]

为了提高简单模型对形状狭长小行星的引力场近似精度,2017 年Zeng 等[64]在链接质点模型和直杆模型的基础上进一步提出了质点连杆模型,即质点间用考虑质量的杆连接.对于两质点的连杆模型,在其质心固连坐标系下,引力势表达式为

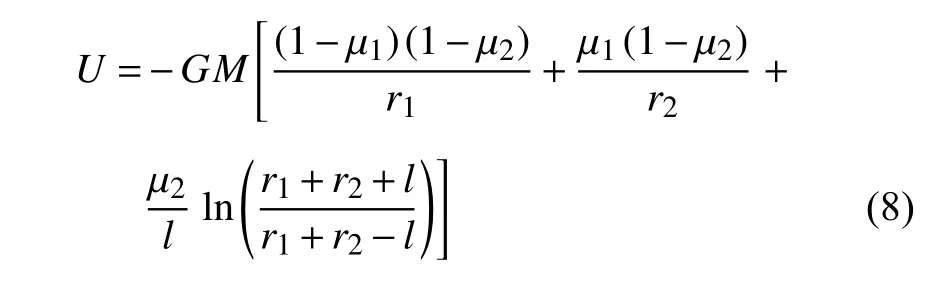
式中,μ1和 μ2分别为质点和连杆质量参数;l为两质点之间距离;r1和r2分别表示场点与两质点之间的距离.

除了上述的几种简单几何模型,在一些研究中还建立了直棒模型[65-66]、匀质圆环和圆盘模型[67-68]、匀质立方体模型[69-70]、非质点哑铃体模型[71-72]等.虽然简单几何体模型对引力场刻画的精度比多面体和质点群模型差,但其表达式具有简单和解析的形式,易于分析动力学特性与模型参数之间的关系,并得到一般性的结论.

需要注意的是,上述引力场模型都具有各自的优势和适用场景,在实际研究中,需要根据研究目标、精度要求和计算量约束进行权衡,选择最为适合的模型,或将不同模型相互结合.

1.2 双星系统相互引力势模型

双星系统的相互引力势模型是研究双星相对运动的基础,其本质是将分属两星的两质量元间的万有引力势对两颗星各求一次体积分,是一个双重体积分.除特殊情况外,两个任意质量分布小行星之间的相互引力势是没有封闭表达式的,通常采用无穷级数展开的方法[73].根据处理双重体积分的数学思路,可以将其分为三类:基于简单几何体的模型、基于刚体质量分布参数的模型和基于多面体形状和刚体质量分布参数的混合模型.

1.2.1 基于简单几何体的模型

典型的双小行星系统通常包含一个快速自旋接近球形的主星和一个被主星潮汐锁定的同步旋转的接近椭球形的次星[74].此时,通常可将其中一颗小行星用匀质球体代替,其万有引力势等价为一个质点的引力势,那么双星的相互引力势就退化为质点在另一颗不规则小行星引力场中的引力势,可利用1.1 节中的不规则引力场模型进行建模计算.

基于这类模型,学者们对双小行星系统的平衡构型和稳定性问题进行了深入的研究.尤其当另一颗不规则小行星也用简单几何体代替时,其相互引力势具有简单的形式,由此可对双星相对运动的平衡构型及稳定性与系统模型参数(如形状尺寸参数、相对距离参数、质量参数等)之间的关系进行定量分析.例如,在研究这类问题时,Scheeres 等[21-22]采用球-椭球模型,李旭等[75]采用了旋转偶极子-球/质点模型.

对该模型另一类重要的拓展,是将其中一颗小行星用质点群法描述,另一颗小行星可采用任意引力场模型,那么双星相互引力势的计算转化为不规则小行星对每个体积元质点的引力势之和.该模型能够大幅提高对双星相互引力的近似精度,尤其是当第二颗小行星采用高精度模型时,但是此时计算也更加复杂,适用于数值研究.例如,Yu 等[45]使用多面体-质点群模型研究了65803 Didymos 的相对运动,并分析了次星受到撞击后抛射物的轨迹和动力学特性.设mi为每个体积元的质量,则双星系统的多面体-质点群引力势为

式中,UPoly为多面体的引力势,见式(4).双星的相互引力和引力矩也具有类似的结构[45].

1.2.2 基于刚体质量分布参数的模型

基于刚体质量分布参数的相互引力势模型是一种经典的描述方法,在研究双星姿态轨道耦合运动中具有广泛的应用,其基本思路是将相互引力势展开为刚体各阶质量分布参数的无穷级数形式.刚体质量分布参数有多种具体的形式,如刚体引力场的球谐系数、刚体惯性积分(二阶惯性积分即为惯性张量)和STF (symmetric trace free)张量等.虽然这些参数形式不同,但本质都来源于刚体质量元坐标的特定表达式对刚体的体积分,也即是反映了刚体的质量分布.

基于刚体质量分布的二体相互引力势的一般形式为

式中,r表示两刚体的质心相对位置矢量; ρ 表示分属两个刚体任意质量元之间的相对位置矢量,满足ρ=r-(h1-h2),Δh=h1-h2,如图7 所示.上式的计算基于两质量元相对位置倒数的级数展开

图7 两刚体相互引力势的几何构型Fig.7 Geometrical representation of mutual gravitational interaction

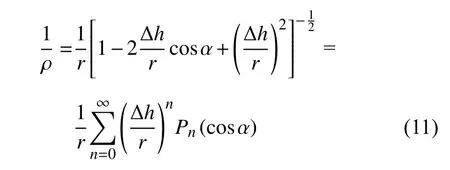
1971年,Giacaglia 和Jefferys[76]基于刚体引力场的球谐系数推导了两个刚体间的四阶相互引力势,但仅考虑到二阶的球谐系数(等价于二阶惯性张量/惯性积分).1979 年,Schutz[77]根据刚体的质量分布推导了两个刚体的四阶相互引力和二阶相互引力矩,但同样也只考虑了刚体的二阶惯性积分.1988 年,Paul[78]推导了两个任意质量分布刚体按惯性积分展开的相互引力势,具有很强的普适性,但是其表达式包含多重复杂的嵌套求和,导致计算复杂.针对Schutz 模型的不足,2007 年Ashenberg[79]推导了完整的四阶相互引力和引力矩,包含了刚体的二阶、三阶和四阶惯性积分.2008 年,Tricarico[80]在Paul 工作的基础上,进一步推导了两个任意质量分布刚体的相互引力和引力矩,同时证明了基于刚体引力场球谐系数和基于刚体惯性积分的两类模型本质上的一致性.2014 年,Compère 和Lemaître[81]推导了基于STF 张量的二体相互引力势,并用于双星姿态轨道耦合动力学的建模和仿真.

另一类基于刚体质量分布参数的模型,由Werner 和Scheeres[73]于2005 年提出,他们将两个刚体均用多面体描述,而且将每个多面体分解为众多四面体的组合,通过质量分布参数计算两个四面体之间的相互引力势,再求和从而得到最终的相互引力模型.2006 年Fahnestock 和Scheeres[23]在此基础上推导了两个多面体之间的相互引力和引力矩,并建立了二体姿态轨道耦合的动力学模型.2013 年,Hirabayashi 和Scheeres[82]进一步建立了各阶级数中形状相关项的递推关系.2017 年,Hou 等[83]利用类似的递推关系建立的模型能大幅提高计算效率.之后Hou[84]对该方法进行了改进,定义了新的广义积分惯量,由此可将积分效率提升至与球谐函数法相当的水平.2018 年,Jiang 等[85]基于上述双多面体相互引力的建模方法计算了两个八面体间四至六阶的引力势,并对二体姿态轨道耦合运动进行了仿真研究.2019 年,Yu 等[86]采用基于双线性四面体元素的有限元方法建立了双星之间的相互引力和引力矩模型.

Werner 和Scheeres[73]在计算两个多面体之间引力势时,首先将每个多面体完全分割成简单四面体组成的实体,以此可将计算相互引力势的二重积分转化为计算A和B两个多面体包含的所有简单四面体对 (a∈A,b∈B) 间的引力势之和,最后得到基于各阶惯性积分/张量的引力势模型[23]

式中,a和b代表两个多面体的面与多面体质心构成的四面体,密度分别为 ρa和 ρb;Ta和Tb为每个四面体局部坐标到惯性坐标变换的雅可比行列式;Q,Qi,Qij和Qijk为常数惯性张量;w和 Δr为与四面体的位置和姿态相关的矢量.该模型能通过调整四面体体积元的密度参数 ρa和 ρb来适应双星密度的不均匀性.

基于刚体质量分布参数的模型能够计算两个任意质量分布刚体间的相互引力,进而建立二体相对运动的姿态轨道耦合动力学模型,具有广泛的适用性.可以通过保留低阶项,对二体相对运动进行理论定性研究;也可以利用高阶的级数展开,得到高精度的相互引力势模型,进行精确的数值研究.

1.2.3 基于多面体形状和刚体质量分布参数的混合模型

2017年,Shi 等[87]提出了基于多面体形状和刚体质量分布参数的混合模型,其基本思路为将其中一颗星建模为匀质多面体,其引力场可采用多面体法进行解析描述,从而将二体相互引力势展开为第二颗星惯性积分的无穷级数.

在多面体小行星的固连坐标系下,将二体相互引力势展开为第二颗星质量分布参数的级数,形式为

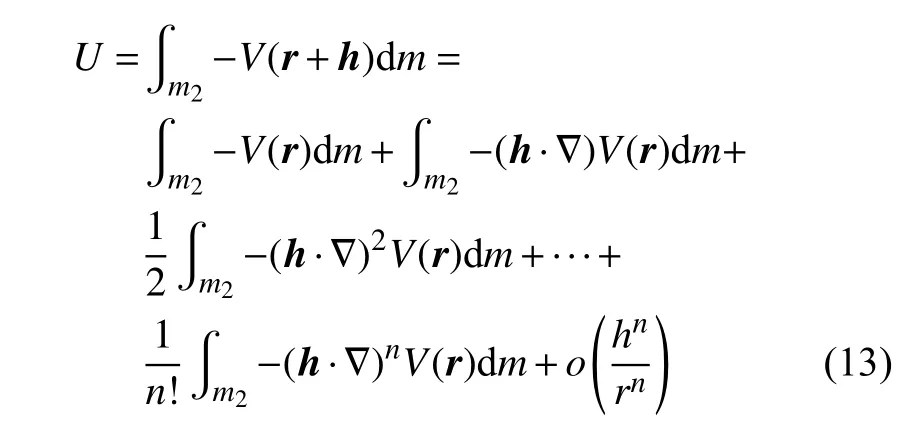
式中,-V(r) 表示多面体引力势,由式(4)给出;r表示双星质心的相对位置矢量;h表示第二颗星质量元相对其质心的位置矢量.式中级数的通项可进一步表示为

式中的积分项即为第二颗星在其固连坐标系下的惯性积分,反映了其质量分布

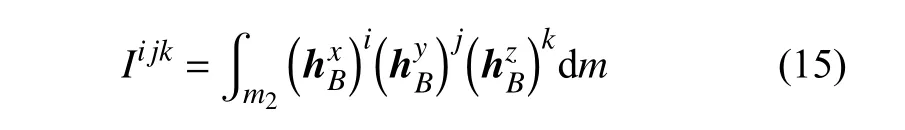
由此,可计算展开到任意阶惯性积分的双星相互引力势.

当展开到二阶项时,双星的相互引力势和引力具有简洁清晰的形式

式中P为与第二颗星二阶惯性积分(即惯性张量)和两星相对姿态相关的矩阵

第二颗星受到的引力矩为

而多面体小行星受到的引力矩可由如下关系得到

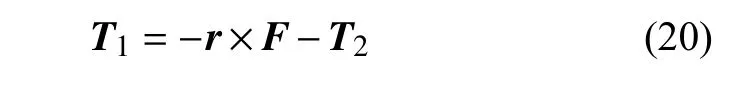
与1.2.2 节中对两个刚体进行惯性积分展开的引力势模型相比,该模型能够对其中一颗星进行不规则引力场的精确建模,避免了同时舍去两颗星的高阶惯性积分.当忽略第二颗星对多面体小行星的引力时,该模型非常适用于描述刚体航天器在小行星不规则引力场中的姿态轨道耦合动力学,其引力模型包含了航天器的质量分布和姿态信息,精度高于经典的将航天器视为质点的多面体引力模型,而引力矩模型则完整包含了多面体小行星引力场的不规则性[88].例如,Lei 等[89]基于该引力矩模型研究了小行星216 Kleopatra 附近航天器的姿态稳定性和姿态周期解.

1.3 双星相对运动的完全二体问题

双星相对运动的完全二体问题本质是两个任意质量分布的小行星在相互引力作用下的姿态轨道耦合运动.在早期的研究中,学者们以分析单小行星旋转分裂后的双星系统动力学演化为目标,重点研究了分裂后的双星在潮汐力等作用下的长期演化过程.本节侧重介绍航天动力学领域对双星相对运动的平衡构型与稳定性的研究成果.在一些简化的相互引力势模型下,双星的相对运动方程具有封闭的解析形式,以此为基础可对系统的平衡构型与稳定性进行解析的研究.

1.3.1 相对运动方程

1995年,Maciejewski[16]在他关于完全二体问题的经典论文中,采用相对位置和姿态坐标,在其中一个刚体B2的固连坐标系中(如图6 所示),给出了具有一般性的二体相对运动的牛顿-欧拉方程

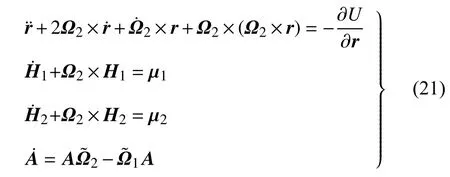
式中,r和A分别为二体相对位置矢量和相对姿态矩阵; Ω1和 Ω2为自转角速 度;H1和H2为自转角 动量;相互引力势的一般表达式为一个双重体积分

μ1和 μ2分别表示两个刚体受到的引力矩,均在B2的固连坐标系中表示,具有形式

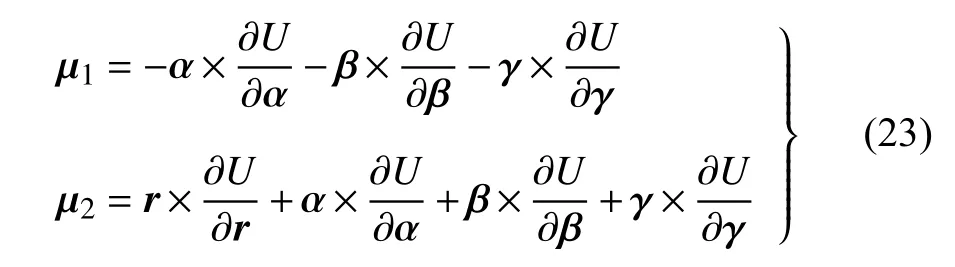
式中 α,β 和 γ 满足

在该模型下,系统存在能量积分和角动量积分.针对双星的简化模型,还能进一步降低系统自由度.例如,在球-椭球二体模型中,可以不考虑球的转动,那么在椭球固连坐标系下,椭球转动的欧拉方程可简化为[26]

如果仅考虑球-椭球的平面运动,利用引力场的空间对称性,可将双星的相对运动简化为一个二自由度的哈密顿系统.2018 年,Hou 和Xin[90]考虑双星相互引力的二阶球谐模型,利用对称性建立了双星平面内的姿态轨道耦合运动方程,并得到了基于轨道偏心率和双星非球形引力一阶近似的解析解.

1.3.2 相对运动的平衡构型与稳定性

双小行星系统需要满足一定的能量和角动量条件才能保证系统的稳定(不发生逃逸或碰撞).双星的姿态轨道耦合运动表明双星平动能量和角动量与转动能量和角动量之间存在转换和约束关系.Scheeres[15]基于此研究了二体系统一般性的希尔稳定性准则和双星避免碰撞的稳定性条件.2009 年,Scheeres[8]在具有空间对称性的二阶相互引力势模型下,给出了量化的系统平面稳定性条件.杜燕如等[20]则研究了双椭球模型下,系统的物理参数(如椭球形状参数、质量比等)对系统平衡态和稳定性的影响.

在双小行星系统稳定(不发生逃逸或碰撞)的前提下,2004 年,Scheeres[21]研究了球-椭球二体模型下系统的平衡构型及其稳定性,在该对称引力场中存在6 种平衡构型,其中椭球绕其最大惯量主轴转动的两种平衡构型如图8 所示,它们具有不同的稳定域,其平面运动稳定性是二体质量比、相对距离和椭球形状的函数.针对长轴平衡构型,对于给定的角动量存在两个稳定性相反(不同能量)的平衡解,Bellerose 和Scheeres[22]研究了这两个平衡解附近的周期轨道族,并且发现高能量状态的平衡解经过能量耗散可转化为低能量状态的平衡解.图9 展示了某一球-椭球二体系统的长轴平衡构型随二体质量比和相对距离变化的稳定性特征,以及给定角动量下长轴构型的稳定和不稳定平衡解(图中数值经过了归一化)[22].

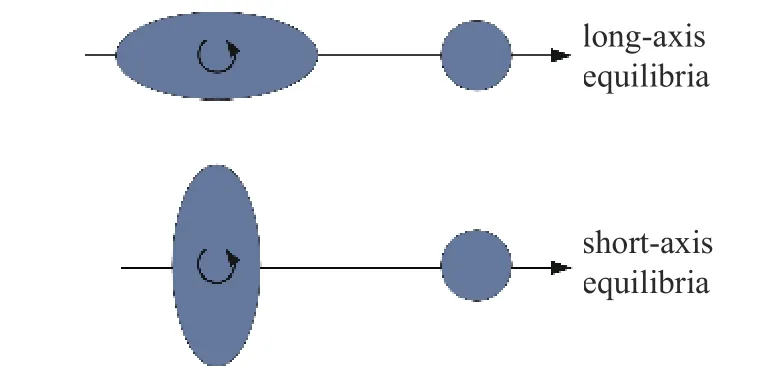
图8 球与椭球二体系统相对运动平衡构型[21]Fig.8 Relative equilibrium configuration of the sphere-ellipsoid two-body problem[21]

图9 球与椭球二体系统长轴平衡构型的稳定[22]Fig.9 Stable parameter space of the sphere-ellipsoid long-axis equilibrium configuration[22]

对于双椭球的平面二体模型,在给定的系统角动量下,不同的系统能量对应了不同的系统稳定状态—决定系统是否发生碰撞和逃逸,同时也对应了不同的双星平衡构型的稳定状态—谱稳定性和能量稳定性[8].2020 年,Wang 和Hou[91-92]从周期轨道的角度,研究了图8 所示的平衡构型下次星(椭球)的天平动,发现天平动振荡幅度与其绕主星的轨道偏心率大小成反向关系.

2 基于限制性三体问题的动力学研究

2.1 轨道动力学模型

在研究航天器在双小行星系统附近的轨道动力学问题时,将主星和次星视为主天体,忽略航天器对两个主天体的引力作用,此时的轨道动力学问题属于限制性三体问题.如上节所述,需要首先确定两颗小行星之间的姿态轨道耦合运动,因此该问题被称为限制性完全三体问题,该问题是对主天体为质点的经典限制性三体问题的推广.与经典问题相比,小行星显著非球形/不规则引力场和系统极小的时空尺度引入了崭新和复杂的动力学特性,为探测器轨道设计带来了新挑战和新机遇.本节主要介绍针对双小行星系统常采用的模型简化方法以及所建立的轨道动力学模型.

现有对系统的简化主要包括两个方面,引力场模型的简化和双星相对运动的简化.在引力场模型方面,可以根据主星和次星的形状特点将其建模为球、椭球等简单几何体,也可以对主星和次星的球谐引力场模型在合适阶次截断.此外,主星和次星可以根据其特点和研究需要选择不同的引力场模型进行组合,从而获得适合的双星系统的引力场模型.Gabern 等[93]将主星简化为固连的三个共线质点,将次星简化为质点/球,这种简洁形式有利于理论研究和解析推导.对于主星形状接近球体的双小行星系统,Bellerose 和Scheeres[25,94]将主星和次星分别简化成球和椭球.Woo 和Misra[95-96]将两颗小行星分别简化成椭球和椭圆台,相比于球-椭球模型引入了模型的非对称性.在双星相对运动方面,对于偏心率较小的双星系统可忽略偏心率,将双星轨道运动简化为围绕公共质心的圆周运动.此外,由于主星具有近似轴对称的特点,对主星快速自旋次星同步转动的单同步双星系统可忽略主星的自旋,假定系统是双同步的.

非同步和单同步双小行星系统附近的力学环境具有时变性,只存在离散分布的、周期与双星自身运动周期满足特定整数比的共振周期轨道.目前的研究大部分是针对双同步的双小行星系统,如图10所示.双同步双小行星系统附近圆型限制性完全三体问题的轨道动力学模型具有和主天体为质点的经典圆型限制性三体问题相似的形式,主要区别在于主天体的引力势表达式

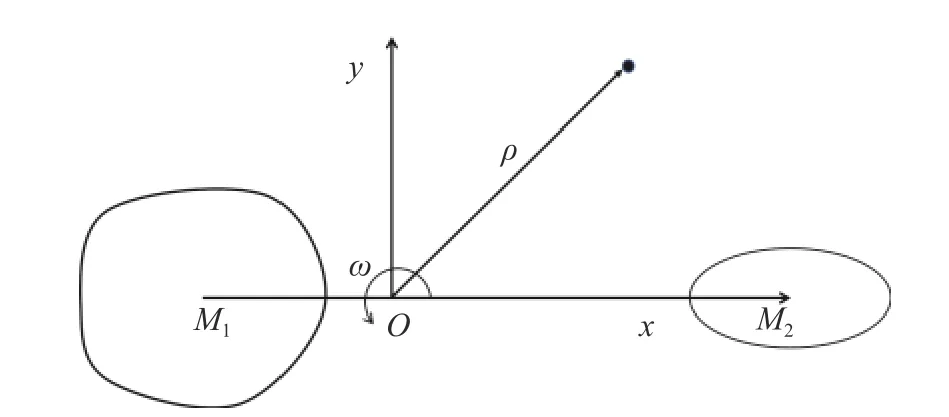
图10 航天器(质点)在双小行星系统附近的轨道运动Fig.10 A massless particle moving in the gravity field of a binary asteroid system

其中U1,U2分别为主星和次星的引力势,下标表示对其求对应的偏导数.

2.2 平动点及平动点周期轨道

对限制性三体问题平动点及其附近周期轨道的研究由来已久,具有很高的理论研究价值和广阔的应用空间.早在1767 年和1772 年,数学家欧拉和拉格朗日在研究主天体为质点的经典圆型限制性三体问题时发现了5 个平动点.1967 年,Szebehely[97]在其专著《Theory of Orbits》中总结了关于圆型限制性三体问题的研究成果,并通过一些数值结果充实了理论研究.1966 到1974 年间,Hénon[98-99]在希尔限制性三体问题模型下对周期和准周期轨道进行了系统的研究,对轨道进行了分类,并研究了各类轨道的稳定性.

在双同步双小行星系统附近的限制性完全三体问题中,同样存在着平动点及其附近的周期轨道,而且小行星的非球形/不规则引力场对平动点及周期轨道存在显著的影响.关于双小行星系统附近平动点的研究主要集中在不同引力场模型下平动点的存在性、位置以及稳定性的差别.将双星均建模为质点或匀质球体时,问题将退化为经典圆型限制性三体问题.2001 年,Sharma 等[100]将主星和次星均假设为刚体,研究了平动点的存在性和稳定性.2006 年,Gabern 等[101]将主星和次星分别建模为球体和椭球体,研究了非球形引力场对平动点位置和稳定性的影响.2005 年～2008 年,Bellerose 和Scheeres[24-27,94,102]对双小行星系统附近的限制性完全三体问题进行了深入研究,将双小行星1999 KW4 建模为球-椭球模型,在长轴平衡情况下计算了平动点,并对平动点的稳定性进行了分析.2018 年,Li 等[103]研究了不同尺寸双椭球模型附近的平动点,并指出平动点的位置受椭球长轴影响较大.这些研究采用的引力场模型均具有一定的对称性,与小行星形状不规则的特点并不完全一致.2014 年,Woo 和Misra[95-96]设计了椭圆台形和花生形等不对称的引力场模型,研究了不同尺寸双星系统的平动点位置与稳定性.球谐函数引力场模型也被一些关注平动点的研究所采用,一些新的现象被发现.2015 年,Hou 等[104-105]采用球谐函数模型近似双椭球系统的引力场,发现系统附近会出现额外的平动点,而直接采用椭圆积分精确计算椭球引力势时则不会产生这种现象,分析发现,额外出现的平动点是球谐函数模型在小行星表面附近误差过大而错误引入的.多面体模型作为一种高精度的小行星引力场模型也被用于双小行星系统附近平动点的研究.2018 年,Shi 等[32]采用双多面体模型对双小行星1999 KW4 进行引力场建模,计算了双星系统附近的平动点和零速度曲面,如图11 所示.可以看到双星系统附近的平动点和零速度面与经典圆型限制性三体问题相似,存在5 个平动点,其中L1,L2 和L3 点对应于经典问题的共线平动点,L4 和L5 点则对应于三角平动点.由于小行星不规则引力场的影响,L1,L2 和L3 点不再严格位于x轴上,而L4 和L5 点的位置也不再与主星和次星构成严格的等边三角形.Bu 等[106]在2017 年研究了双椭球模型的双小行星系统在连续小推力作用下的人造平动点及其稳定性,并借助零速度曲面研究了小推力对可达域的影响.此外,对于非同步的双星系统,由于系统的时变性,不存在严格意义上的平动点,只存在瞬时的“平动点”,可被称为动力学替代(dynamical substitutes).Shi 等[32]计算了双小行星系统1999 KW4 在主星快速自旋的单同步情况下的瞬时平动点,通过对比发现瞬时平动点在z方向的变化小于在x和y方向的变化,而且主星的自旋并未改变平动点的稳定性.2018 年,Hou 和Xin[90]将双星建模为两个刚体,双星相互引力势保留至二阶,在平面完全二体问题一阶解析解的基础上构建了限制性三体问题模型,并求解了其中的共线平动点.

图11 双多面体模型下双星系统1999 KW4 附近的零速度面与平动点[32]Fig.11 Zero velocity curves and libration points of the binary asteroid system 1999 KW4[32]

经典限制性三体问题的平动点周期轨道已经有了非常深入和广泛的研究,并应用于实际飞行任务.双小行星系统附近限制性完全三体问题的平动点周期轨道也吸引了不少学者的关注.

2015年,Chappaz 和Howell[28]利用多段打靶法得到了球-椭球和椭球-椭球双同步双星系统附近的平面Lyapunov 轨道,垂直Lyapunov 轨道,南向和北向的Halo 轨道,如图12 所示.数值计算结果表明,双同步双星系统平动点周期轨道的结构和经典圆型限制性三体问题类似.由于球和椭球模型的引力场具有对称性,平动点周期轨道也具有和经典问题一样的对称性,具体体现在平动点周期轨道关于双星连线的对称性,南向和北向Halo 轨道的对称性,以及L4 和L5 平动点轨道的对称性.而在更高精度的非对称引力场模型下,平动点周期轨道虽然和对称模型下的轨道相似,但是轨道的对称性和各族轨道之间的连接关系会发生显著变化.2017 年,Dell’Elce等[31]采用双椭球模型研究了双小行星系统65803 Didymos 的二体运动,之后通过多面体-椭球模型研究了双小行星系统附近的周期轨道.2018 年,Shi等[32]将双小行星系统1999 KW4 建模为双多面体模型,在双同步情况下求解了平动点和平动点周期轨道,发现受到不规则引力场的影响,平动点周期轨道族的分岔情况与经典圆型限制性三体问题完全不同.图13 为经典问题和双小行星系统平动点周期轨道族连接方式的对比,可以看到在双小行星附近,Lyapunov 轨道族发生了断裂,分别与南北向Halo 轨道融合.Capannolo 等[30]在2019 年采用多面体-椭球模型研究了双小行星系统65803 Didymos 附近的周期轨道族,包括平动点L1 和L4 附近的Lyapunov 轨道,Halo 轨道以及短周期轨道(short period orbit,SPO),并分析了不同主星姿态对轨道的影响.Zhang 等[107]在2020 年借助多面体-椭球模型研究了次星形状的不确定性对平动点及平动点周期轨道的影响,发现次星形状的变化将导致平动点位置的变化,稳定性可保持不变,而周期轨道族的分岔情况会发生显著改变,南北向Halo 轨道不再与平面Lyapunov 轨道融合,而是与垂直Lyapunov 轨道融合.此外,轴向轨道也与垂直Lyapunov 轨道断裂后的不同部分相融合,而不像经典问题中那样两端分别连接平面Lyapunov 轨道和垂直Lyapunov 轨道,如图14 所示.

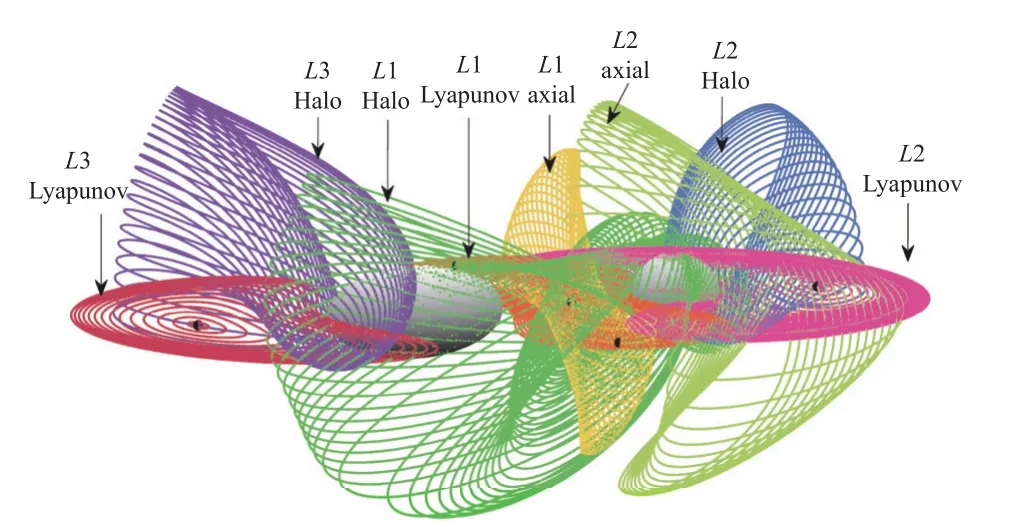
图12 双椭球模型中的平动点轨道族[28]Fig.12 Libration point orbits (LPO) in the ellipsoid-ellipsoid model[28]

图13 不同模型下平动点周期轨道族连接方式[32]Fig.13 Connections of libration point orbits in different dynamical model[32]

图14 不同次星形状时平动点轨道族连接情况[107]Fig.14 Connections of libration point orbit families with different shapes of the secondary[107]

单同步双小行星系统主星的快速自旋导致系统是非自治的,动力学模型具有时变的特点.此时双星系统附近虽然不再存在完整的周期轨道族,但仍存在一些与主星在会合坐标系中自旋周期满足特定整数比的共振周期轨道.Shi 等[32]在单同步模型下通过微分修正求解得到了满足特定周期条件的共振周期轨道,如图15 所示.Shang 等[108]在2017 年借助拉格朗日拟序结构(LCS)研究了非同步球-椭球双星模型附近的轨道,将发现的15 种轨道分为了四类:短暂轨道、逃逸轨道、撞击轨道和飞掠轨道.

图15 单同步双星系统L1 点和L2 点附近的周期轨道[32]Fig.15 Periodic orbits near L1 and L2 about the single synchronous binary asteroid system[32]

在双星系统附近,除共线平动点外,学者们对三角平动点L4 和L5 附近的轨道动力学也进行了研究.Liang 等[109]研究了双小行星系统三角平动点区域的动力学和稳定区域,将双小行星系统1999KW4简化为经典圆型限制性三体问题,发现在雅克比常数在特定区间时存在两个稳定区域,后续在球-椭球模型下发现了可以围绕L4 点14 天以上的有界轨道.Hou 等[110]在2020 年将双星系统建模为两个三轴椭球,研究了受太阳光压力时三角平动点附近的轨道运动,发现即使对较小面质比的航天器,受迫周期轨道也可以有很大的振幅.

2.3 其余类型的周期轨道

由于平动点轨道往往位于天体的一侧,适用于对天体某一区域的持续观测,但如果需要对双小行星系统进行全面探测,就需要考虑其他类型的周期轨道.除了受到广泛关注的平动点周期轨道外,双星系统附近还存在大量其他类型的周期轨道,比如围绕主星和次星的周期轨道,与双星轨道运动具有共振关系的共振周期轨道,以及围绕双星系统的大范围周期轨道等.不同类型的周期轨道各具特点,可以根据探测任务的需要选作名义轨道,对双小行星探测任务设计具有重要意义.

对于不规则引力场中的周期轨道求解问题,数值搜索是一种有效且全面的手段,Yu 等[111]在2015 年提出了一种单小行星附近的周期轨道搜索算法,并将该算法应用于小行星216 Kleopatra,得到了29 族周期轨道.2019 年,Shi 等[33]对该算法进行了改进,得到了适用于双小行星系统的搜索算法,搜索得到了双小行星系统1999 KW4 附近大量的周期轨道,其中就包括围绕主星和次星的周期轨道,如图16 所示.此外,Shang 等[29]在2015 年借助双椭球同步双星系统中的对称性,通过搜索算法得到了双小行星809 Lundia 附近的30 族周期轨道和双小行星3169 Ostro 附近的28 族周期轨道,并分析了轨道的稳定性以及潜在的应用前景.

图16 双小行星系统1999 KW4 中部分围绕主星和次星的周期轨道[33]Fig.16 Periodic orbits about the primary and the secondary in the binary asteroid system 1999 KW4[33]

在围绕次星的周期轨道中存在一种逆行轨道,即远距离逆行轨道(DRO).该类轨道在1968 年由Broucke[112]在地月系统中发现,属于稳定周期轨道,因其在探测任务中具有广阔的应用前景而受到了众多学者的关注.双小行星系统附近的DRO 也得到了特别关注.2015 年,Chappaz 和Howell[28]将双星系统建模为球-椭球系统,并对DRO 进行了数值计算以及稳定性分析.Capannolo 等[113]在2017 年研究双小行星65803 Didymos 附近的探测器编队飞行问题时考虑了DRO,在2018 年利用多面体-椭球模型研究双小行星系统65803 Didymos 附近的周期轨道时考虑了围绕次星的DRO,并分析了不同主星姿态角对DRO 的影响.Jean 等[114]在2019 年研究太阳光压力对双星系统附近轨道影响时也将DRO 作为主要研究对象之一.

在限制性三体问题中还存在一种具有较高应用价值的周期轨道,即与主天体轨道运动具有共振关系的共振周期轨道.DRO 在幅度较大时也属于共振周期轨道的一类.2014 年,Vaquero 和Howell[115]对地月系统中共振轨道的动力学结构进行了深入细致的分析,得到了平面及三维共振轨道,并提出利用共振轨道实现低能转移.2016 年,Feng 等[116]对相连双小行星附近动力学环境进行了分析,发现了三类不同共振比的共振轨道.Chappaz 和Howell[28]在2015 年借助球-椭球模型和双椭球模型研究了双星系统附近的平面及三维共振轨道,并分析了这些轨道的稳定性.图17 给出了Chappaz 和Howell[28]得到的平面共振轨道,其中1:1 共振轨道即是前文提到的DRO.2019 年,杨雅迪等[117]将双小行星1999 KW4 建模为双椭球模型,计算了共振比1:1,1:2,1:3,1:4 和2:3 的平面和三维共振轨道,分析了共振轨道周期和能量的变化规律.

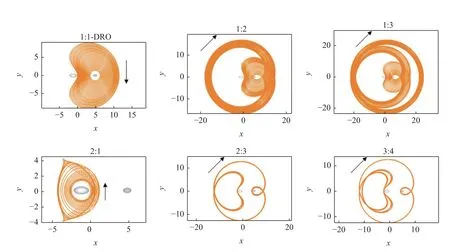
图17 双小行星双椭球模型下的平面共振轨道[28]Fig.17 Planar resonant orbits in the ellipsoid-ellipsoid model[28]

除共振周期轨道外,还存在着一些围绕双星系统的大范围周期轨道,可用作双小行星探测的初始停泊轨道或者长期远距离探测轨道.Shi 等[33]在2019 年借助双多面体模型搜索双小行星系统1999 KW4 附近的周期轨道时,得到了许多围绕整个系统的大范围周期轨道,如图18 所示.

图18 围绕双小行星系统1999 KW4 的大范围周期轨道[33]Fig.18 Period orbits with wide range around the binary asteroid system 1999 KW4[33]

2.4 转移轨道研究

在双小行星探测任务中,转移轨道是必不可少的重要环节,高效安全的转移轨道可以为双星系统的全面探测提供有力保障.目前,对探测器在双小行星系统内的轨道转移研究较少,主要针对同步双小行星系统进行了转移轨道设计,此时系统与经典圆型限制性三体问题类似,可以类比采用经典问题中的方法解决.Ferrari 等[118]使用不同三体问题的拼接研究了探测器的转移轨道,将双小行星系统的主星用固连的两个质点代替,将次星视为质点,将主星附近的轨道运动和远离主星的轨道运动分别用两个圆型限制性三体问题模型来近似,根据两个三体问题不变流形的分布特征,采用流形拼接方式设计了全局的低能转移轨道和小行星表面的起飞或着陆轨道.Chappaz 和Howell[119]求解了球-椭球模型下平动点轨道的稳定与不稳定流形,研究了同步双星系统中的同宿和异宿转移轨道,将2:3 共振轨道以及围绕主星和次星的轨道作为探测轨道,通过微分修正设计转移轨道将探测轨道连接起来,从而实现双星系统的全局探测,如图19 所示.

图19 球-椭球模型下的全局探测路径[119]Fig.19 Exploration trajectories in the sphere-ellipsoid model[119]

2.5 周期轨道维持

由于任务名义轨道的不稳定性以及入轨偏差、未建模摄动力、导航误差及推力误差等各类扰动,探测器的飞行轨迹通常会偏离所设计的名义轨道,需要进行轨道维持.除了面临经典限制性三体问题的共性问题外,双小行星系统附近的轨道维持需要考虑更多的约束,面临更大的困难.首先,由于观测条件和精度的限制,小行星运动状态的观测比行星要困难许多,有很强的不确定性,名义轨道无法在更高精度模型中做进一步的优化,与实际飞行轨迹相差更大,对轨道维持能力提出更高要求.其次,小行星的引力场非常微弱,探测器受到的扰动相对更为显著,更容易偏离名义轨道.最后,双小行星系统的时间和空间尺度都远小于地月系统或日地系统,偏离名义轨道后若没有及时修正,将很快发生逃逸或撞击.因此,双小行星系统附近的轨道维持需要更高的控制精度和频率.2014 年,Woo 和Misra[96]在圆锥台-椭球模型下计算了平动点L2 和L4 附近的轨道,并通过设计线性反馈控制器实现了轨道维持.2018 年,Li 等[34]通过双椭球模型计算了双星的相对运动,从而建立了非同步情况下双椭球系统附近的轨道动力学模型,将同步模型下的周期轨道作为初值,计算了非同步模型下的有界轨道,并将其作为任务名义轨道,设计了一种自适应的轨道维持控制律.上述研究均采用了连续推力方式.2020 年,Shi 等[35]将主星建模为多面体,次星视为具有二阶质量分布参数的刚体,对双星系统的相对运动进行了仿真,计算了双星处于激发态和平稳态两种情况下围绕主星、次星的轨道和L1 点Halo 轨道的演化,发现在激发态情况下,即使稳定的名义轨道也会迅速发散,如图20 所示.接着设计了基于目标点法和离散LQR 法的两种脉冲式轨道维持策略,发现活跃态情况下维持消耗要显著大于平稳态,改进后的目标点法在脉冲消耗和脉冲间隔上的表现要优于离散LQR 法,更适合双小行星系统附近的轨道维持.图21中给出了L1 点Halo 轨道在平稳态与活跃态系统中采用目标点法实现轨道维持时的情况.2019 年,Guzzetti 等[36]研究了太阳帆航天器在双小行星系统中的人造平动点及拟周期轨道,并设计了一种通过调整太阳帆姿态角实现L4 点区域轨道维持的控制策略,可以实现数周的维持.

图20 名义轨道在平稳态(上)与活跃态(下)系统中的轨迹[35]Fig.20 Trajectories of nominal orbits in the dynamical systems with relaxed mode (up) and excited mode (down)[35]

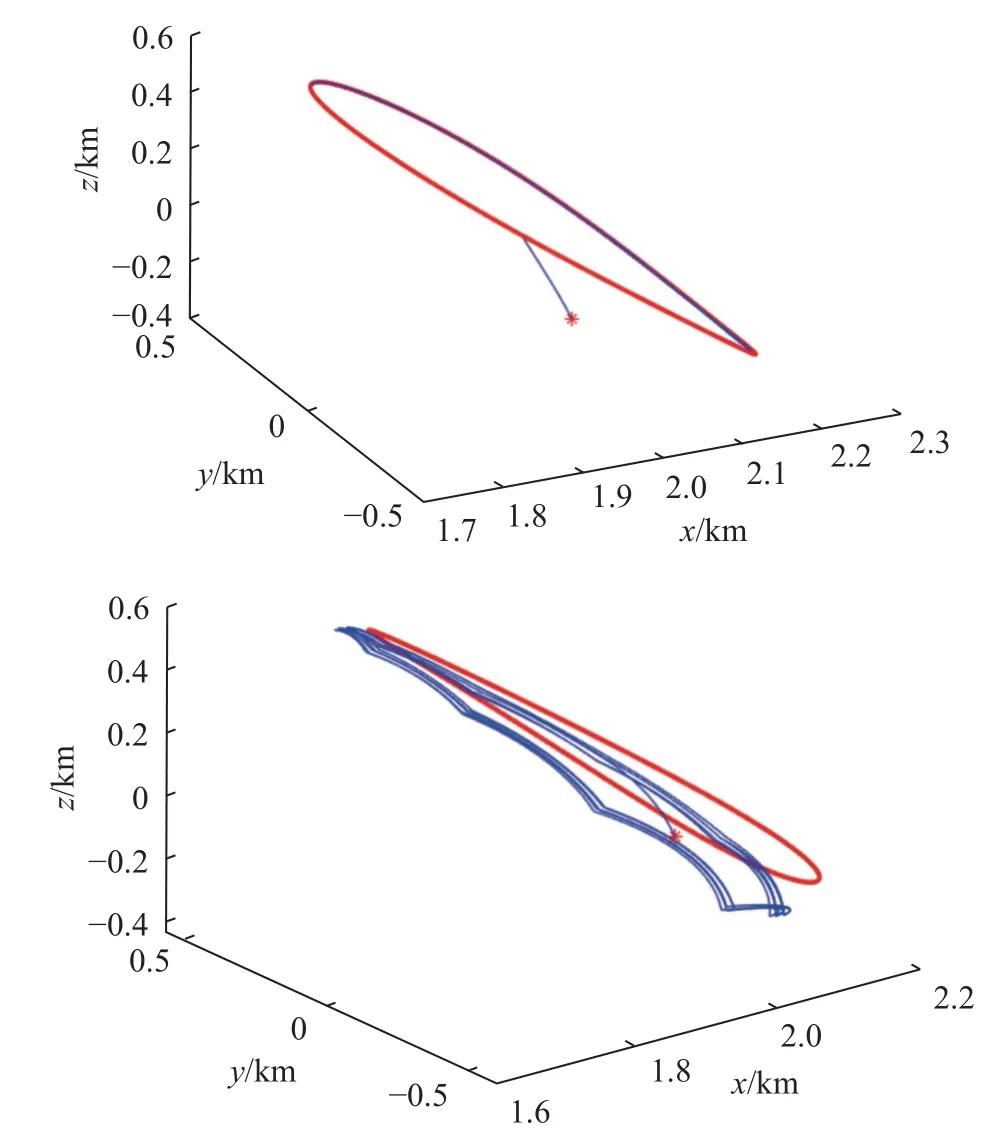
图21 L1 点Halo 轨道在平稳态(上)与活跃态(下)系统中采用目标点法实现轨道维持[35]Fig.21 The trajectories during the stationing-keeping in the dynamical systems with relaxed mode (up) and excited mode (down) by using the target point method with the L1 Halo orbit as nominal orbits[35]

3 基于受摄二体问题的动力学研究

上一节着重介绍了在限制性三体问题框架内,平动点及平动点周期轨道、大范围周期轨道、转移轨道和周期轨道维持等方面的研究现状.这些研究是对球形主天体的经典限制性三体问题的自然推广.然而事实上,在双小行星附近的轨道动力学中,还存在对更为经典的受摄二体问题的推广,即环绕系统单颗星的轨道动力学.本节将针对环绕双星系统单颗星的环绕型轨道动力学问题,即受摄二体问题的研究进行综述,以受摄二体问题为主线,首先引入经典的轨道摄动理论和太阳系行星系统中受摄二体问题的相关研究成果,并以此为基础介绍环绕双小行星系统单颗星的轨道动力学研究.

3.1 受摄二体问题的动力学模型及基本解法

历史上对受摄二体问题的研究始于17 世纪末对太阳系行星和行星天然卫星轨道运动的研究.在跨越近两个世纪的时间里,涌现了诸如牛顿、欧拉、拉格朗日、拉普拉斯等一大批的天才科学家,他们致力于解决月球轨道理论和行星轨道稳定性等难题;到了近现代,1957 年第一颗人造地球卫星的发射,极大地拓展和丰富了轨道摄动理论的发展和应用.长久以来,对摄动问题的求解方法形成了三种基本的类型:特殊摄动法,一般摄动法和半解析法.

3.1.1 特殊摄动法

特殊摄动法(也称直接法)是指借助数值法求解轨道运动的微分方程,得到基于轨道初始条件的特定解.数值法以Encke 法和Cowell 法为代表.

19世纪前期,Encke 提出了建立密切轨道与参考轨道(无摄动的开普勒轨道)偏差的运动微分方程并进行数值积分的方法,而不直接求解包含中心引力和摄动力的完整运动方程[120].基于该方法建立的摄动方程为

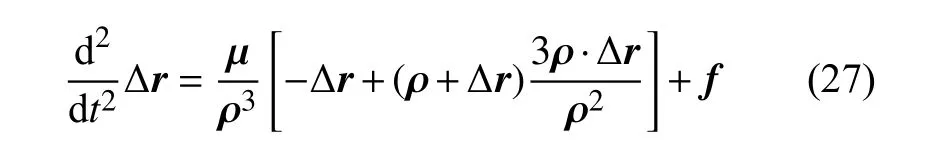
式中,ρ 表示参考轨道的位置矢量; Δr为真实位置与参考位置的偏差矢量;f表示摄动加速度.Encke 法的优势在于,由于偏差的变化缓慢,数值积分可采用更大的步长,易于获得高精度的数值解.但这种优势被现代计算机的强大计算能力所掩盖,因此该方法在如今的研究中应用较少.

20世纪之前,受计算机能力的限制,数值法没有受到太多的关注,直到Cowell 对摄动轨道方程(形如式(28),被称为Cowell 公式)采用直接数值积分,成功定位了八颗木星卫星的轨道,并且对哈雷彗星在1759 年～1910 年三次回访中的两次进行了成功的预测[120]

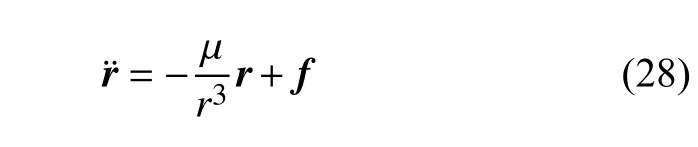
利用上式,可以方便地将任意的摄动力添加到轨道的运动微分方程中(线性叠加).而且,得益于现代计算机的强大性能,基于Cowell 公式进行数值求解仍然是现代摄动轨道计算的常用方法.

特殊摄动法虽然形式和原理上都比较简单,而且可以得到精确的数值解,但是获得的解依赖于轨道初始条件和具体的模型参数,难以推广到更广泛的问题中.

3.1.2 一般摄动法

一般摄动法是指用解析方法求解摄动轨道的运动微分方程,从而得到具有普遍性的解.解析法是最早被用于轨道摄动研究的方法,可以追溯到17 世纪牛顿在《自然哲学的数学原理》中对月球轨道运动的研究和描述.在此后的两个多世纪里,克莱罗、汉森、德洛纳、希尔、布朗和埃克特等先后研究了月球的轨道运动理论,最终建立了非常精确的月球运动模型[121].

在航天动力学中,一般摄动法大多以轨道要素的摄动方程为出发点,而轨道要素变化微分方程的建立则是以常数变易法(variation of parameters,VOP)为基础.VOP 的数学方法最早由欧拉提出,其基本思想是用无摄动系统的解(常量)来表示相应摄动系统的解,不过这些未摄动常量需要替换为随时间变化的量.1782 年拉格朗日将VOP 应用到轨道的摄动问题中,建立了针对经典轨道要素的拉格朗日行星方程[122]

式中,n为平均轨道运动;R为摄动函数(摄动势能的相反数).拉格朗日行星方程仅适用于摄动力为保守力的情况.

对于摄动力为非保守力的系统,或者即便是保守力,也可采用摄动力分量的形式来建立相应的摄动运动方程,这种形式的方程称为高斯摄动方程.为方便研究,可将摄动力在不同的坐标系下分解,例如将其沿轨道径向、横向和轨道面(副)法向分解(S,T,W型);或沿切向、主法向和副法向分解(U,N,W型),从而能够得到两组不同的轨道摄动方程,具体表达式可参考文献[122]的第三章.

在轨道摄动方程中除了采用经典轨道要素,还可采用米兰科维奇轨道要素:角动量矢量H、拉普拉斯矢量L(可转换为偏心率矢量e)和一个表示沿轨道运行时间的标量,分别建立拉格朗日型和高斯型的摄动运动方程[123].矢量形式的方程具有结构紧凑和几何意义直观的特点,能够清晰地反映轨道运动的某些动力学特征.

对于哈密顿系统,还可建立正则形式的轨道摄动运动方程.在轨道力学中通常采用的正则共轭变量是德洛纳(Delaunay)变量:L,G,H(角动量),l,g,h(角变量),它们与经典轨道要素之间的关系为[122]

针对上述正则变量的摄动运动方程为[122]

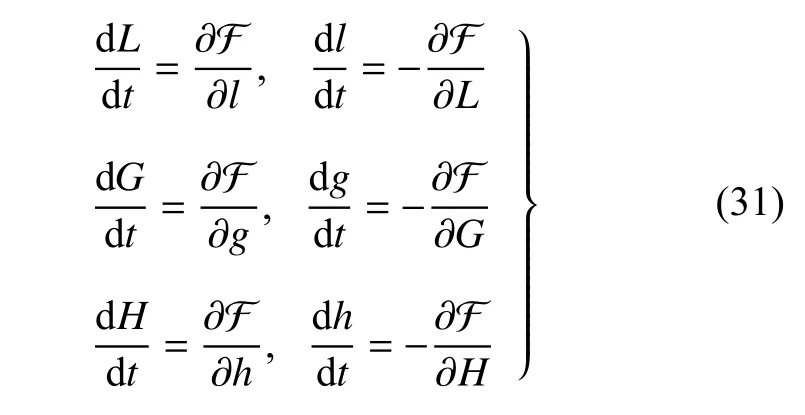
式中 F 为哈密顿函数.

按照上述方式建立的轨道摄动运动方程都是复杂非线性的,难以得到其准确的解析解.但是由于摄动均为小量,可将摄动力展开为小参数的幂级数形式,由此可构造摄动运动方程的小参数幂级数解,这种求解方法称为摄动法[122].在摄动法的基础上,日本天文学家古在(Kozai) 最早给出了改进的摄动法——平均根数法[124].该方法首先将摄动变化项拆分为长期项、长周期项和短周期项,构造摄动幂级数解采用的参考轨道不再是初始轨道对应的无摄动椭圆轨道,而是采用包含长期变化的椭圆轨道,即长期进动椭圆,相应的轨道根数称为平均根数.平均根数法在求解地球扁率、中心天体非球形引力、第三体引力和太阳光压力等作用下的摄动幂级数解中具有重要的应用.

3.1.3 半解析法

鉴于数值法计算的复杂性和寻找解析解的巨大困难,20 世纪60 年代平均化方法被应用到受摄轨道研究中,基于该方法建立的针对摄动长期项和长周期项的轨道运动模型称为半解析模型.平均化方法消除了轨道摄动的短周期项,一方面在数值积分时可采用更大的积分步长,提高计算效率;另外,半解析模型在分析轨道长期演化的动力学特征和揭示轨道演化的一般性理论方面具有巨大的优势,有着广泛的应用[125-127].

在早期的研究中,通过分离出摄动函数中与快变量(平近点角) 无关的项[128-129],或者通过高斯(环) 平均化方法[130]来实现短周期摄动项的分离.1961 年,Bogoliubov 和Mitropolsky[131]提出了用于非线性动力学系统渐近分析的Krylov-Bogoliubov-Mitropolsky 平均化方法,利用该方法能够以更加简单直接的方式消除方程中的短周期项.例如,对摄动函数的平均化可以表述为

式中,M为轨道平近点角; α 代表其他轨道要素和变量.将平均化后的摄动函数代入到拉格朗日行星方程中,就得到了轨道的长期摄动方程;或者对摄动力进行平均化,再利用高斯摄动方程相应能得到高斯型的长期摄动方程.

以矢量要素形式的长期摄动方程为例,其表达式具有简洁对称的结构[132]

式中,h和e分别表示归一化的角动量矢量和偏心率矢量;表示平均化和归一化的摄动函数.同样,将平均化后的哈密顿函数代入到正则形式的摄动方程(30)中,也能得到基于Delaunay 正则变量的轨道长期运动方程.

基于上述消除短周期项的轨道长期摄动运动方程,借助一些分析方法和数值方法,就能够对轨道摄动运动问题展开研究,下一节将具体介绍.

3.2 受摄二体问题的动力学特性研究

在复杂摄动力作用下,航天器环绕中心天体的轨道可能发生长期变化,因此分析轨道变化的规律对于任务设计和长期维持策略都具有重要的意义.一方面要尽量避免摄动力对轨道产生重大的影响,通过分析轨道的稳定性、设计冻结轨道等来保证轨道的长期稳定;另一方面,也能利用轨道摄动的进动特征,设计某些特殊类型的轨道,如太阳同步轨道.在不同的天体系统中,系统参数不同,不同类型摄动力的相对大小也不同,航天器轨道将具有不同的演化特征,这里主要阐述环绕地球轨道和环绕其他行星或行星卫星轨道的相关研究.

3.2.1 近地轨道的长期演化动力学

1957年第一颗人造地球卫星的发射,极大地推动了对轨道摄动问题的研究.1959 年,Brouwer[128]和Kozai[129]几乎在同一时间研究了低轨道卫星在地球非球形引力摄动下的轨道运动,计算获得了短周期项、长周期项和长期项的近似解析解,推动了卫星轨道理论的发展.但是他们的研究没有考虑大气阻力的作用,而对于低轨卫星大气阻力有显著的影响.后来的学者们在他们研究的基础上不断发展改进,相关理论被成功应用到工程实践中.

对于中高轨道的人造地球卫星,不仅受到地球非球形引力的摄动,日月第三体引力的摄动作用也非常显著.1964 年,Allan 和Cook[132]考虑了地球扁率和日月第三体引力摄动,利用式(33)所示的半解析模型,研究了圆轨道的进动效应,发现各摄动力会致使轨道平面绕摄动轴进动,最终效果为轨道平面绕着某一合成摄动轴进动,如图22 所示.

图22 轨道平面法向量在单位球面上的进动轨迹[132]Fig.22 Trajectories of the orbit pole on the unit sphere[132]

在早期的工程实践中,人们利用轨道演化特性,通过合理配置轨道初始状态来实现轨道的长期稳定[133].其中,冻结轨道是一类重要的研究对象,它可以最大限度节省轨道维持所需的燃料[134-135].例如,地球低轨卫星在地球引力带谐项为主要摄动力的环境下,J2临界倾角(6 3.4°和1 16.6°)附近的轨道能够保持近地点(偏心率和近地点幅角)的稳定[136-140],但随着轨道高度的增加,日月第三体引力的显著作用会导致近地点高度的振荡和近地点位置的变化[141-142].当轨道半径位于3 至10 倍地球半径范围时,地球扁率和日月第三体引力的摄动都不能忽视,形成了与低轨卫星不同的动力学环境.Ulivieri等[134]研究了这个范围内圆轨道的冻结轨道方案,Circi 等[135]利用矢量描述的方法研究了类似场景下椭圆轨道的冻结轨道.

3.2.2 环绕其他行星或行星卫星的轨道动力学

自20 世纪70 年代以来,轨道的长期摄动理论还被拓展到环绕月球的轨道和其他行星系统中,用于第三体引力的长期摄动作用[126,143-144]、冻结轨道[135,145-146]、轨道稳定性分析[147-148]和维持轨道长期稳定[149-150]等方面的研究.在不同的系统中,由于具有显著不同的系统参数,轨道的长期演化呈现出不同的特征.例如,月球和金星等天体球谐引力的扇谐项或高阶带谐项,会导致基于J2项得到的临界倾角值发生较大改变[151-152].某些系统中,强烈的第三体引力摄动会引起高倾角轨道的极不稳定,致使轨道寿命的大幅缩减[127,147,153].在大多数以中心天体引力J2项和第三体引力为主要摄动力的行星系统中,轨道稳定性差异本质是由这两种摄动力的相对强弱决定的.Scheeres 等[147]定义了一个参数来表征这两种摄动力的相对大小,并研究了不同比值下轨道的稳定性.Delsate 等[145]研究了针对该系统参数变化的系统平衡点(冻结轨道)的分岔,如图23 为平衡点分岔线,将模型参数空间分成了不同的区域,在每个区域内系统的平衡点、相空间结构及稳定性都具有不同的特征,可以发现系统除了 ω =±π/2 的Lidov-Kozai 平衡点外,还存在 ω =0 和 π 的中心和鞍点两类平衡点.

图23 系统在参数空间 ( κ,) 中的分岔Fig.23 Bifurcation lines in the parameter space(κ,)

轨道的长期摄动理论在近地空间碎片的轨道分析、碎片减缓和再入预报等方面具有重要的应用.与在役卫星保持长期轨道稳定的目标正好相反,人们希望空间碎片能够在自然摄动力的作用下尽快实现大气再入,释放轨道资源.空间碎片减缓在20 世纪90 年代已有研究[154-155].近年来,Wang 等[156-158]研究了通过设置发射时间调整日月第三体引力摄动的相位和利用日月长期共振等实现空间碎片寿命的减小.

3.3 Lidov-Kozai 动力学机制

Lidov-Kozai 机制是天体力学中的一个重要轨道动力学现象,描述在圆轨道第三天体引力摄动下(也被称为层级圆型限制性三体问题),当受摄二体问题轨道(即受摄开普勒轨道)倾角大于某一特定值时,轨道偏心率和轨道倾角存在大幅耦合振荡,且近地点幅角/轨道拱线可在平衡点附近往复振荡,对轨道全局演化和稳定性产生重要影响.这一机制还被拓展到椭圆轨道第三天体引力摄动下的受摄二体问题,即层级椭圆型限制性三体问题,发现了偏心Lidov-Kozai 机制,将导致轨道在顺行和逆行间发生翻转.另外,在摄动第三天体位于所研究轨道内部时(即所谓外问题),Lidov-Kozai 机制仍然存在,被用于海王星外天体的轨道演化研究.

3.3.1 经典Lidov-Kozai 机制

1961年,Lidov[159]在层级圆型限制性三体问题的构型下研究了环绕地球的轨道动力学,发现经过两次平均化后,结合系统守恒量(轨道角动量垂直分量和轨道能量),系统自由度可降为一,系统可积.此时,系统呈现出两个有趣的动力学现象:(1)轨道偏心率和轨道倾角存在长期耦合振荡;(2)轨道倾角大于某一临界倾角(3 9.2°)时,近地点幅角可能在±90°附近往复振荡,不再持续进动.系统的运动可通过两个积分常量 (c1,c2) 完全确定

其中c2决定了拱线进动的特征.当c2＜0 时,近地点幅角处于振荡状态;当c2＞0 时,近地点幅角单调变化,如图24 所示.

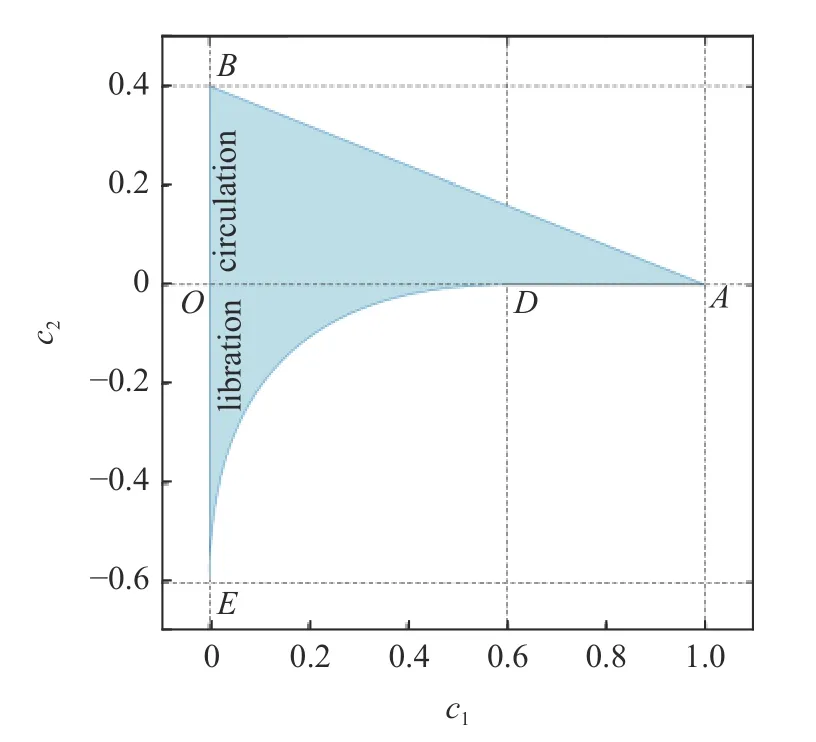
图24 二次平均化模型下的两个轨道积分常量[160]Fig.24 The two orbit integral constants under the doubly-averaged model[160]

1962年,Kozai[125]基于相同的层级圆型限制性三体问题构型,在研究木星引力摄动下主带小行星环绕太阳的轨道运动时得到了类似的结论.因此,这一动力学现象被称为Lidov-Kozai 机制.在该机制下,高倾角近圆轨道的偏心率将经历长期大幅振荡,致使轨道非常不稳定[161].接着Lidov[161]和Kozai[162]进一步考虑了中心天体的扁率摄动,发现了其对Lidov-Kozai 机制的抑制作用.而且,扁率摄动会引起Lidov-Kozai 平衡点的分岔以及新平衡点的出现,从而改变系统的稳定性特征[145,147].Lidov-Kozai 机制被广泛地应用到行星不规则卫星、彗星、近地小行星和系外行星的形成和演化研究[163-169]以及航天器轨道动力学研究[143,145,147].例如,“热木星”形成的原因可能是Lidov-Kozai 机制促使其轨道偏心率增长,“近星点”不断靠近中心恒星,最终在长期的潮汐耗散作用下形成稳定的热木星[165-166].

3.3.2 偏心Lidov-Kozai 机制

Lidov-Kozai 机制的另一个重要拓展是解除“圆型”限制,在层级椭圆型限制性三体问题的构型下,系统呈现出新的丰富的动力学现象.此时,摄动第三天体位于椭圆轨道上,系统的轴对称性消失,轨道角动量的垂直分量不再是守恒量,系统不可积.基于二阶近似的第三体引力摄动模型不能准确描述这种非对称性,而必须考虑引力摄动的三阶项[170].1969 年,Harrington[171]对三阶近似模型进行积分,发现了系统的共振和混沌等动力学现象.2000 年,Ford等[172]考虑了摄动天体轨道的大偏心率(ep=0.9),发现轨道在Lidov-Kozai 长期振荡的基础上,还存在周期更长的振荡,导致轨道偏心率的极大增长.2011 年,Naoz 等[173]首次发现在椭圆轨道第三体引力摄动下,轨道平面可能在顺行(i＜90°) 和逆行(i＞90°)之间发生周期性翻转,并且翻转时伴随着偏心率非常接近1,如图25 所示,这被用来解释部分逆行“热木星”的形成.这种动力学行为被称为偏心Lidov-Kozai 机制.

图25 偏心Lidov-Kozai 机制下的轨道翻转[170]Fig.25 Orbit flip of the eccentric Lidov-Kozai mechanism[170]

之后,Litchwick 和Naoz[174]与Katz 等[175]对轨道翻转发生的条件分别进行了数值和解析研究.Li 等[176]研究了椭圆轨道第三体引力摄动下系统的混沌现象.Naoz 等[170,177]对偏心Lidov-Kozai 机制在系外行星、恒星系统和黑洞系统动力学演化方面的重要作用进行了综述.

3.3.3 外问题中的Lidov-Kozai 机制

实际上,层级限制性三体问题,即第三天体引力摄动下的受摄二体问题,可分为外问题和内问题,如图26 所示.因为绝大多数层级三体系统都具有内问题的几何构型,即摄动天体位于目标天体轨道外侧,所以对外问题的研究相对较少.1975 年,Ziglin[178]在层级椭圆型限制性三体问题的构型下,较早地研究了行星环绕双恒星系统的轨道运动.之后,学者们在二阶近似摄动模型下,发现了外问题中不同于传统内问题Lidov-Kozai 机制的高倾角平衡点[179-180],可以用来解释HD 98 800 恒星系统极轨道上稳定粒子的存在.2017 年,Naoz 等[181]将偏心Lidov-Kozai机制拓展到外问题中,同样发现了轨道的翻转现象.外问题的轨道摄动模型还能用于研究行星外离散盘、奥尔特云和海王星外天体等的轨道演化[182-183].

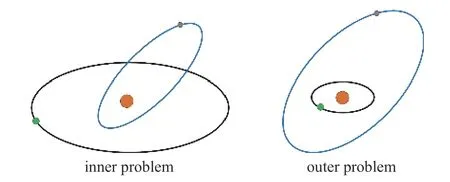
图26 层级三体问题中的内问题与外问题Fig.26 The inner and outer problem in the hierarchy three-body system

3.4 环绕双小行星系统主星的轨道演化

2020年,Wang 和Fu[40]将前述受摄二体问题的理论和方法拓展到双小行星系统中,研究环绕双星系统单颗星的轨道长期演化.与上述经典的受摄二体问题不同,双小行星不仅为中心天体引入了非球形引力,而且为第三天体引力摄动也引入了非球形项.此外,中心天体和摄动天体极近的距离一方面导致第三天体引力摄动的高阶项非常显著,传统希尔近似不再适用,需保留高阶项,另一方面使得中心天体非球形引力摄动的主导区域和第三天体引力摄动的主导区域高度重合,导致了不同摄动力的强烈耦合.在笔者的研究中,系统的几何构型如图27 所示,主星为探测器所环绕的中心天体,次星为摄动第三天体,假设次星轨道为圆形,即为层级圆型限制性三体问题.在动力学建模中,首次在第三天体引力摄动函数中包括了主星和次星的非球形引力项.针对第三天体引力摄动高阶项显著的特点,将次星引力摄动势函数保留至四阶,其形式为[40]

图27 双小行星的二体构型和环绕主星的轨道[41]Fig.27 The two-body configuration of the binary asteroid system and orbits around the primary[41]

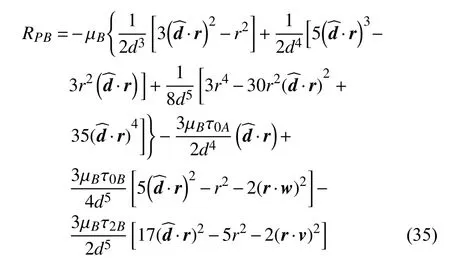
式中,τ0A表示主星的扁率作用项,τ0B和τ2B表示次星的二阶球谐引力项.从上式可以发现,主星和次星的非球形引力项分别出现在第三天体引力摄动的三阶项和四阶项中.

将四阶近似的轨道运动方程针对航天器轨道和次星轨道进行两次平均化,发现由于系统具有轴对称性,轨道角动量的垂直分量守恒,系统的自由度可降为一,系统可积.基于二次平均化的轨道运动方程具有形式

式中,fe和fω分别表示相应变量的函数,具体的表达式可参见文献[41];第三式表示轨道角动量的垂直分量守恒,其数值可由初始条件确定.

此外,需要注意的是,在行星系统中较少讨论的关于平均化有效条件的问题,在双小行星系统中则会凸显:较强的摄动会导致轨道在一个平均化周期内较大程度地偏离开普勒轨道,使得平均化失效.Wang 和Fu[40]利用数值方法研究了保证平均化有效的摄动力大小需满足的限制条件.在较高精度要求下,可近似认为中心天体扁率和第三体引力摄动大小与中心天体质点引力大小的比值需小于10-2量级.另外,航天器轨道运动与次星轨道运动不发生共振,且航天器轨道进动周期相对次星轨道周期较大.

在基于方程(36)描述的动力学模型下,能够进一步分析包括轨道稳定性在内的动力学特性,发现在Lidov-Kozai 机制和中心天体扁率摄动的共同作用下,J2临界倾角附近的轨道具有较强的不稳定性,如图28 所示[41],但对于这类轨道仍然可以通过将轨道初始近地点幅角置于“长驻留点”(满足)处,以延长轨道寿命[41,150],如图29 所示;而高倾角和低倾角轨道近地点高度振荡的幅度较小,且可通过设置轨道的初始条件来维持轨道的小偏心率状态.

图28 J2 临界倾角附近的 ω -e 相空间轨迹[41]Fig.28 ω -e phase trajectories around the J2 critical inclination[41]

图29 不稳定轨道的轨道寿命[41]Fig.29 The orbital lifetime of unstable orbits[41]

上述针对环绕主星轨道的研究是在次星圆轨道且次星位于主星赤道面内的条件下进行的,实际的双小行星系统中次星轨道可能还具有偏心率,且次星轨道平面可能倾斜于主星赤道平面,这两个因素都将破坏系统的对称性,使得轨道角动量的垂直分量不再是守恒量,系统不可积,包括混沌和高阶共振在内的非线性动力学特征将对轨道运动产生显著影响.最新的研究表明,在考虑次星轨道偏心率的层级椭圆型限制性三体问题中,探测器轨道平面存在不同于传统偏心Lidov-Kozai 机制的轨道翻转,如图30所示.可以发现,与偏心Lidov-Kozai 机制相比(如图25),中心天体的J2摄动一方面会导致允许翻转的轨道倾角范围缩小,但另一方面导致允许翻转的轨道偏心率降低,使得轨道可在更低的偏心率下完成轨道平面的翻转,拓宽了轨道翻转的场景.该动力学特征不仅可用于解释双小行星系统附近粒子特异的轨道演化行为,对于揭示系外行星系统形成和演化机制也具有重要的应用价值.

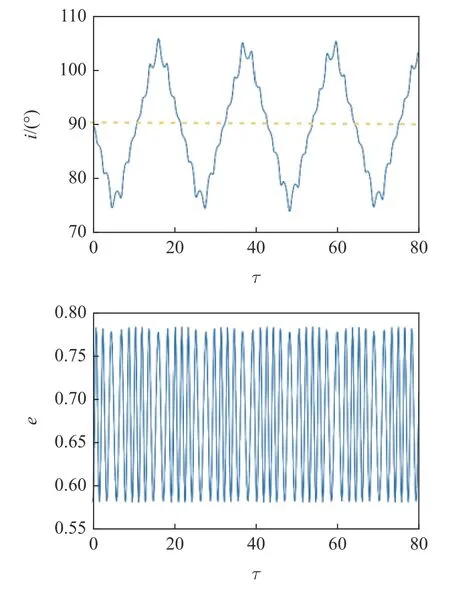
图30 J2 摄动的层级椭圆型限制性三体问题下的轨道翻转Fig.30 Orbit flip in the hierarchical elliptical restricted three-body problem with the J2 perturbation

4 面向任务的轨道动力学分析与设计

前面章节介绍的研究大多是基于简化力学模型的理论研究.在实际的双小行星探测任务中,探测器轨道设计不但要考虑更加真实的力学环境,还要满足任务目标和探测器平台性能等诸多约束条件.目前,以双小行星系统为目标的任务中,除了已发射的DART 探测器(AIDA 第一阶段),另有处于立项研制阶段的Hera 探测器(AIDA 第二阶段)和Janus 任务,它们具有各自明确的探测对象、任务目标和探测器属性.本节主要介绍针对这些任务需求,在实际力学环境和相关的约束下,对探测器轨道动力学的分析和轨道方案的设计.

4.1 任务轨道设计研究

4.1.1 基于周期轨道的任务轨道设计

周期轨道是深空探测活动中具有重要应用价值的轨道,不同类型的周期轨道能够满足特定的任务需求,同时能够以较少的燃料消耗进行轨道维持.在双小行星系统附近,周期轨道提供了可靠的探测轨道,是探测任务轨道设计的重要参考.但是复杂的摄动力可能增加周期轨道的不稳定性,因而实际的任务轨道需要在接近真实的力学环境中进一步改进计算得到,并进行轨道稳定性的分析.

2017年,Dell’Elce 等[31]针对AIDA 探测任务,找到了两类具有鲁棒性的周期轨道——围绕主星的内部逆行轨道和围绕整个双星系统的晨昏轨道,内部逆行轨道适合对主星的观测,晨昏轨道提供了对双星大范围的观测,如图31 所示.Capannolo 等[30]在高精度的引力场模型下,研究了系统附近多种类型的周期轨道,可满足不同的任务需求,例如多种尺寸的远距离逆行轨道(DRO)可实现稳定且大范围的次星环绕,L1和L2平动点轨道能够实现对次星局部区域的近距离观测,如图32 所示.

图31 绕双星65803 Didymos 晨昏轨道(从太阳方向看)[31]Fig.31 Terminator orbits around the binary asteroid system 65803 Didymos seen from the Sun direction[31]

图32 双小行星系统65803 Didymos 附近的周期轨道族[30]Fig.32 Periodic orbits in the binary asteroid system 65803 Didymos[30]

周期轨道的求解可基于不同精度水平的动力学模型,模型的精度越高,计算得到的周期轨道就越接近真实轨道,轨道维持所需的燃料消耗也往往更少[184].Shi 等[35]以双小行星系统66391 Moshup(即1999 KW4)为例,比较了各类轨道维持方法的优劣和有效性,计算了各类周期轨道的轨道维持所需的燃料消耗,其结果可为任务轨道设计提供参考.

4.1.2 面向特定任务需求的任务轨道设计

AIDA 任务第一阶段是由DART 探测器抵达双小行星系统65803 Didymos 并对次星实施撞击.然而若只有单一的探测器,对撞击后的观测只能由地面远程开展.2018 年,Capannolo 等[185]提出由DART 探测器携带并释放一个微纳卫星用于撞击后的观测,以获得更多的科学数据.为了满足对撞击坑和喷溅物观测的良好条件,在微纳卫星安全性、相机性能等诸多约束条件下,对释放立方星的时刻、相对速度大小和方向进行了优化设计,验证了该方案的可行性.最新进展表明,DART 探测器携带了一个由意大利航天局(ASI)负责的6 U 立方星LICIACube,其主要任务是实施对撞击坑和喷溅物的观测和对次星形状的测量等[186].为此,Capannolo 等[187]针对LICIACube 的具体参数,结合撞击坑模型和喷溅物扩散模型,考虑平台和任务目标的约束条件,将轨道设计问题转换为以立方星释放方向为优化变量的优化问题,得到了相应的轨道方案,并且对不确定性因素进行了鲁棒性分析.

AIDA 任务第二阶段由Hera 探测器于撞击四年后到达该双小行星系统,对撞击坑和轨道偏转等特征进行观测和测量.Hera 任务的实施可分为远距离初步测量阶段和近距离详细探测阶段,G i l-Fernandez 等[188]根据任务特定需求,分别分析和设计了满足任务约束(如脉冲机动频率、脉冲大小、轨道高度、光照条件和安全裕度等)的远距离和近距离双曲线飞掠轨道,如图33 所示,图中闭合的轨迹由几段双曲线轨道连接构成,可通过不同的组合调整近星点高度和次星的纬度覆盖范围.基于类似的方法,Ferrari 等[189]对仅覆盖双星系统光照面的两点和多点往复飞掠轨迹进行了详细的研究,分析了近星点高度、所需的推进剂消耗和轨道机动频率,以此为依据可选择满足任务需求的轨道.

图33 Hera 探测器的双曲线飞掠轨迹设计Fig.33 The hyperbolic fly-by trajectories design of Hera mission

4.2 转移轨道与弹道着陆轨道研究

在双小行星探测任务中,由于双星系统附近强摄动的复杂力学环境,主探测器靠近双星可能存在较大的风险.为了实现近距离和表面探测,有科学家提出采用成本更低、体积更小的微纳卫星方案,例如AIDA 任务中DART 探测器携带的6 U 立方星LICIACube;Hera 探测器计划携带的两个6 U 立方星,其中一个为着陆器.因为微纳卫星的轨道机动能力有限,所以基于不变流形的低能转移和着陆轨道成为必要的选择.

2013年,Tardivel 和Scheeres[190]在双星视为质点的经典圆型限制性三体问题模型下,研究了利用平动点附近动力学特征的无控着陆轨道,并将理论应用到MarcoPolo-R 任务(已取消)的备份目标双小行星系统1996 FG3 中,设计了可靠性较高的L2平动点到次星表面的弹道着陆轨道[191].2016 年,Wu 等[192]在双小行星系统90 Antiope 的双同步椭球模型下,将双星的表面选择为庞加莱截面,通过稳定和不稳定流形拼接实现双星之间的轨道转移,如图34 所示.Celik 和Sánchez[193]采用从小行星表面着陆点开始的反向积分方法研究了主星和次星的弹道着陆轨迹,该方法具有很强的灵活性,可以在不同约束下快速规划出满足约束条件的着陆轨道.

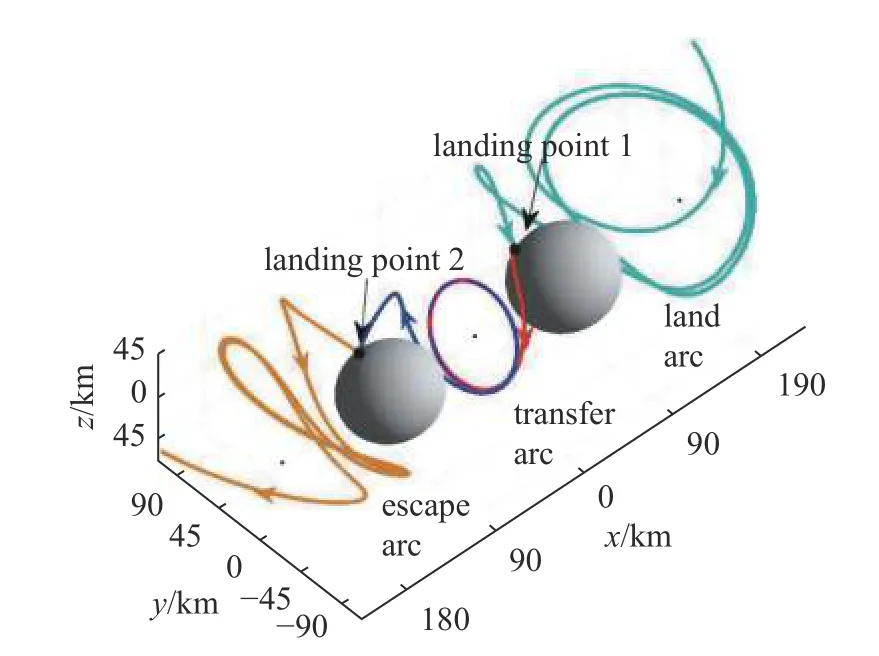
图34 双小行星系统90 Antiope 成员之间的转移轨道[192]Fig.34 The spatial transfer orbits between the two bodies of the binary asteroid system 90 Antiope[192]

5 总结与展望

双小行星系统的独特构型和复杂引力场环境为探测任务设计带来了极大挑战,首当其冲的就是强摄动耦合环境中的轨道动力学特性分析与任务轨道设计.经过近三十年的研究,人们对双小行星系统附近的轨道动力学已有了较为全面的认识,但仍有一些问题需要进一步的研究和解决.

首先,双小行星系统的不规则引力场建模是探测器轨道动力学研究的基础.目前已经形成了比较成熟的描述双星不规则引力场的方法,如质点群法、球谐函数法、多面体方法,以及基于特定简单几何体的引力场近似方法.在这些方法中,计算简单和高精度往往是一对矛盾,未来可针对特定场景将不同建模方法结合,形成兼顾计算效率和精度的混合方法.另外,在探测器达到目标前,小行星准确的形状和质量信息未知,难以对其引力场进行精确建模,需要依靠探测器逐步抵近和测量,不断提高引力场建模精度,才能确定最终的轨道方案.因此,未来需要研究通过星载计算机的有限资源,实现对双小行星系统高效、精确甚至实时的引力场测量和计算.在双星系统相互引力势方面,目前已经形成了基于不同原理的建模方法,可以满足双星相对运动的理论和数值研究,未来可针对如何提高计算效率进行进一步的改进和提高.在双星相对运动方面,目前已较为全面地揭示了平衡构型及其附近的动力学特性,由于大部分双星系统处于平衡构型附近,因此目前可以满足探测器轨道动力学研究的需要,未来可针对更精细或更长期的动力学演化特性开展研究.

基于限制性三体问题的双小行星系统附近轨道动力学研究目前主要包括动力学建模、周期轨道求解与分析、转移轨道设计和周期轨道维持等内容.动力学建模方面,小行星引力场模型的精度从质点/球模型、椭球模型、球谐函数模型到多面体模型精度不断提高,逐渐逼近小行星的真实引力场.周期轨道方面,学者们对平动点及平动点周期轨道、共振周期轨道、围绕某颗星或整个双星系统的周期轨道进行了大量研究,主要关注了轨道族计算,以及稳定性和分岔等动力学特性.转移轨道方面,目前已在不同动力学模型下通过流形拼接等方法实现了不同区域间的转移,但大部分研究未考虑实际任务的需求和约束.周期轨道维持方面的研究主要包括连续推力和脉冲推力两种形式,但目前所尝试的维持策略种类较少,未来可进一步借鉴经典限制性三体问题中的新型维持策略,并根据双小行星系统的特点加以改进,得到性能更优的轨道维持策略.

限制性三体问题的周期轨道较不稳定,形成条件苛刻,几何构型和分布较为固定,一定程度上限制了其在长期、近距离探测中的应用潜力.而基于受摄二体问题的环绕双小行星单颗星的轨道稳定性相对较好,形成条件较为宽松,分布更为广泛,并易于实现对小行星的全球覆盖,在长期、近距离探测和稳定停泊方面具有很大的应用价值,因而在最近受到了关注.已有的研究主要包括环绕主星的半解析轨道动力学建模和在此基础上进行的轨道稳定性分析等.目前,该方向的研究刚刚起步,很多问题尚未解决,未来需要系统性地发展.例如,未来可研究小行星非对称非球形引力项、太阳光压力、太阳引力和次星轨道偏心率等对轨道稳定性的影响;还可将环绕单颗星的内问题拓展到环绕整个双星系统的外问题,推动对双小行星系统附近轨道动力学的理解,为探测任务提供更多的轨道类型选择.

进入21 世纪的第三个十年,双小行星探测将进入实践阶段.针对目前已经立项研制的双小行星探测任务,学者们在探测目标、任务要求和实际约束等因素的综合考量下,进行了面向实际任务的轨道动力学分析与轨道设计.周期轨道能够提供多种类型的观测轨道,可满足不同的任务需求,结合轨道维持策略,能够保证轨道的安全性和可靠性,具有一定的应用潜力.另外,针对低成本微纳卫星变轨机动能力的限制,研究了基于不变流形的低能转移和着陆/起飞轨道.实际上,目前处于工程实施阶段的探测任务出于安全性的考虑,对主探测器都拟采用飞掠或往复飞掠轨道,极大限制了探测效率和探测精度.因此,未来需要基于双小行星附近轨道动力学研究的最新成果,在复杂力学环境和多种任务约束下,提出探测效率、探测精度和安全性等综合性能更优的轨道设计方法和控制技术.

综上所述,目前对双小行星探测轨道动力学的研究已经形成了比较成熟的理论体系,但某些研究方向刚刚开展,尚待系统性地发展,在比较成熟的研究方向,也仍有一些理论和技术问题尚待解决或完善.此外,需要将探测任务设计和轨道动力学的最新研究成果更好融合,从而提升探测任务的综合效能.随着双小行星探测任务的不断推进,在检验现有理论、方法和技术的同时,还将涌现出更多的科学和技术问题,将不断推动轨道动力学理论、轨道设计方法和轨道控制技术的发展.