一种自适应骨干细菌觅食优化算法
2022-06-15朱永杰李冰晓万睿之赵新超左兴权
朱永杰,李冰晓,万睿之,赵新超*,左兴权
(1.北京邮电大学 理学院,北京 100876;2.北京邮电大学 计算机学院,北京 100876)
细菌觅食优化算法(Bacterial Foraging Optimization,BFO)是由Passion提出[1],是一种简单有效的随机全局优化算法,不但有良好的局部搜索能力,算法中的迁徙操作还可以避免算法陷入局部最优.该算法因群体并行性及易跳出局部最优等优点,已经成为群体智能研究领域的一个重要分支.BFO近几年在算法设计、理论分析与应用研究方面取得长足发展.2009年Shao和Chen[2]通过协作方法提出了一个BFO算法变种,即合作细菌觅食优化(CBFO)算法;Chen等[3]提出了自适应细菌觅食优化算法,采用自适应搜索策略显著提高了原算法的性能;刘小龙等[4]通过引入分布估计思想以及对细菌赋予自适应迁徙概率,提出了一种基于高斯分布估计的细菌觅食优化算法;Jarraya等[5]提出了一种简单的方案来适应细菌觅食优化算法的趋化步长,然后将新的适应方法与粒子群优化和差分进化结合构成在一种新的混合方法,采用差分进化策略进行自适应趋化细菌群觅食优化;Dasgupta等[6]从经典梯度下降搜索的角度提出了对BFOA趋化步骤的理论分析,并且为了加快接近全局最优解的细菌群的收敛速度,提出了两种简单方案调整趋化步长;Wang等[7]采用近似局部最优和自适应突袭的渐进式开发策略,提出了一种新的BFO算法变种;杨大炼等[8]通过改进细菌种群大小、细菌运动步长、引进迭代终止条件改进原有细菌觅食算法,然后将其应用到支持向量机的参数优化问题;刘小龙等人[9]通过赋予细菌灵敏度的概念,对细菌游动的步长进行调节以提高收敛速度,采用免疫算法中的克隆选择思想,对精英细菌群体进行克隆、高频变异和随机交叉,引导算法提高搜索精度;李珺等[10]根据菌群的进化代数提出改变迁徙操作的作用范围,避免逃逸发生,提出在复制操作中,按照细菌个体当前适应度值的优劣进行复制,更准确地实现了细菌个体的优胜劣汰,进一步提高收敛速度;Kim等[11]提出了一种混合遗传算法和细菌觅食算法的函数优化方法;Datta 等[12]根据自适应增量调制原理提出了自适应趋化步长的 BFO 算法;Tang等[13]通过在细菌觅食优化算法中引入PSO算法基本思想,提出了快速细菌群算法;Dasgupta等[14]将差分进化算法的交叉与变异操作引入BFO算法,提出一种混合型全局优化算法.细菌觅食算法也广泛应用于多目标优化领域.Guzman等[15]提出一种基于大肠杆菌趋药性过程的多目标优化算法,该算法利用快速非支配排序过程、群体成员之间的通信和简单的趋化策略来改变细菌的位置,以探索搜索空间来寻找多个最优解;Niu等[16-18]先后提出将细菌觅食算法应用于多目标优化问题中.
本文第1节介绍标准细菌觅食优化算法;第2节简单介绍骨干粒子群算法;第3节详细介绍提出的新算法的结构框架和简要分析;第4节在CEC2014测试函数集上,对提出的基于骨干思想的自适应细菌觅食优化(BBBFO)算法与标准细菌觅食优化(BFO)算法和文献[19]中具有协同差分进化的细菌觅食优化算法(PDBFO)进行仿真对比试验;第5节给出结论和进一步的可能问题.
1 标准细菌觅食优化算法
细菌觅食优化(BFO)算法是一种基于种群的随机搜索算法.该算法主要模拟人体肠道中大肠杆菌搜索食物的过程,主要包括三个运动行为:趋化、繁殖和迁徙行为.BFO算法对以上生物行为仿真建模,解决复杂非线性优化问题.
趋化性操作:趋化主要包括两个行为,翻转和游动.细菌向任意方向移动单位步长为翻转;细菌沿着上一步的运动方向移动单位步长为游动.细菌在营养物质丰富的环境中聚集或在有毒物质的环境中逃避的过程中,首先向任意方向移动单位步长到达新位置,如果到达的新位置适应值不如上一次位置的适应值,那么细菌就沿任意方向翻转;否则,就沿相同方向持续移动,直至适应值不再改善或达到最大游动次数.新位置的更新公式如下:
θi(j+1,k,l)=θi(j,k,l)+C(i)φ(j)
(1)
(2)
其中θi(j,k,l)为第i个细菌在第j次趋化,第k次复制,第l次迁徙时的位置,C(i)为游动的步长,φ(j)为翻转后随机选择的单位方向向量,△(i)为翻转时方向调整后选定的方向向量,向量中的元素在区间[0,1].
复制性操作:趋化操作完成后,通过模拟细菌运动行为中的繁殖现象,提出了复制操作,对每个细菌在生命周期内的适应度值进行累加获得细菌能量.细菌能量公式如下:
(3)
其中Jihealth表示第i个细菌的能量,Nc表示趋化次数.细菌适应度值越大,能量越大,表示细菌越健康,觅食能力越强.所以将细菌能量按从小到大的顺序,淘汰掉前一半能量小的细菌,保留后一半能量大的细菌,并且复制后一半细菌,生成与后一半细菌完全相同的子代细菌.
迁徙性操作:复制操作完成后,对种群中细菌i,给定概率Ped,生成一个区间为(0,1)的随机数r,如果满足r 粒子群算法PSO是一种基于种群搜索的智能算法[20],是通过模仿鸟群觅食的行为而产生的一种仿生算法.PSO算法中每一个个体称为一个粒子,代表一个潜在解,每个粒子通过追踪当前种群中的全局最优解GBest和个体最优解PBest来产生新的粒子,从而实现搜寻问题的最优解.设群体规模为N,粒子维数为m.第t代粒子i的位置为Xi(t)=(xi1(t),xi2(t),…,xij(t),…,xim(t)),i=1,2,…,N,速度为Vi(t)=(vi1(t),vi2(t),…,vij(t),…,vim(t)),粒子迄今搜索到的个体历史最优值为PBesti(t)=(Pbesti1(t),Pbesti2(t),…,Pbestij(t),…,Pbestim(t)),全局最优为GBesti(t)=(gbest1(t),gbest2(t),…,gbestj(t),…,gbestm(t)).于是,粒子按式(4)、(5)更新位置和速度: vij(t+1)=wvij(t)+c1r1j(pbestij(t)-xij(t))+c2r2j(gbestj(t)-xij(t)) (4) xij(t+1)=xij(t)+vij(t+1) (5) 其中,w为惯性权重,c1和c2为加速算子,r1j和r2j是在[0,1]上均匀分布的随机数. Kennedy等人[21]在2003年提出了骨干粒子群(BBPSO)算法,将PSO的速度和位置更新公式改进为一个无参数公式: (6) 粒子的位置随机地以pbestij(t)和gbestj(t)的平均值为均值,以两者的欧氏距离为标准差进行高斯变异.在优化初期,粒子散布于解空间中,标准差较大,算法倾向于全局搜索,优化后期,标准差逐渐减小,算法倾向于局部搜索.并且每个新解产生的中心和方差依赖于自己的历史最优位置,从而新解产生具有动态自适应调整的优势. 用细菌觅食算法求解最优化问题时,每个细菌采用固定步长进行游动,若固定步长较大,则可能导致后期细菌跳离最优解所在邻域,出现收敛速度慢、精度低的问题;若固定步长较小,结果精度较高,但收敛速度太慢,易陷入局部极值而难以跳出.因此,算法搜索过程中需要选取合适的游动步长以保证其收敛速度、结果精度以及防止其陷入局部最优邻域无法跳出.因此本文设置细菌第m次游动的步长如式(7)所示: (7) 其中Ns为细菌游动的最大次数,Xmax和Xmin分别是变量的上下边界,λ是根据问题的搜索区域进行设置.该适应性动态调整的步长公式在算法初期取值相对较大,从而具有勘探整个搜索空间的可能性;随着算法进行,步长逐渐适应性减小,从而对先前发现的优秀邻域进行小范围开发,具有较快的新解生成收敛速度. 由于基本BFO的复制操作使得种群多样性大大降低,受骨干粒子群算法的启发,将骨干思想融入复制操作.具体操作描述如下:将细菌能量Jhealth按从大到小的顺序排列X1,…,XS,淘汰掉后S/2个能量值较小的细菌,后Sr个细菌新位置是以前S/2个细菌的重心为均值μ,以X1与XS/2的欧氏距离为标准差δ,通过高斯采样逐个得到.后S/2个细菌新位置更新公式如下: (8) (9) (10) 该组细菌新位置的公式有如下优点,一是较为充分的利用了群体优质解的信息,从而产生优质数据驱动的进化动力;二是利用半种群优质解作为新解产生中心而不是利用单个最优解,避免了有可能的局部陷阱的吸引;三是新位置产生的高斯公式的标准差的动态调整契合了算法前期大范围勘探、后期小范围搜索的一般规律. 本文沿用经典的细菌觅食优化算法模型,基于骨干思想的自适应调整机制嵌入标准的细菌觅食算法趋化操作和复制操作中,新算法的主要实现步骤描述如下. Step1 参数初始化.细菌规模数S,趋化次数Nc,复制次数Nre,迁徙次数Ned,游动次数Ns,迁移概率Ped. Step2 初始化细菌位置.采用公式X=Xmin+rand·(Xmax-Xmin)产生初始化位置,计算细菌的初始化适应值J. Step3 迁移循环l=1:Ned;复制循环k=1:Nre;趋化循环j=1:Nc. Step4 执行细菌趋化循环 (1)翻转:按照公式(1)、(2)更新细菌位置. (2)游动:如果翻转的适应值得到改善,则细菌按照翻转的方向以公式(7)作为游动步长继续向前游动,直至适应值不再改善或者达到设定的最大游动次数Ns. Step5 繁殖循环.趋化周期完成后,按照公式(3)对每个细菌在生命周期内的适应值进行累加得到细菌能量,按照细菌能量排序,淘汰掉能量小的半数细菌,对能量大的半数细菌按照公式(8)进行高斯变异,替换淘汰掉的半数细菌,保持细菌总数不变. Step6 迁徙循环.繁殖算子完成后,生成一个随机概率,并将它与固定的迁徙概率Ped进行比较,如果小于Ped细菌进行迁徙,在解空间的定义域内随机初始化. Step7 循环结束条件判断,满足则结束,输出结果. 为了验证本文提出的基于骨干思想的自适应细菌觅食算法(BBBFO)的性能,选取测试函数采取CEC2014测试函数集[22]将BBBFO与标准的BFO和PDBFO进行对比分析. 在CEC2014测试函数集[22]的各类函数中选出代表性算例构成本文的基准测试函数集,所有测试函数均为高维可伸缩的函数.选取 CEC2014 函数简介如下,f2,f3为单峰函数,f5,f6,f10,f11,f15为多峰函数,f20,f21,f22为混合函数,为了方便起见,将这些函数重新标记为F1~F10.这些测试函数详细信息见文献[22]. 算法对比实验的具体参数设置如下:细菌规模数S=40,搜索空间维度D=30,趋化次数Nc=40,复制次数Nre=4,迁徙次数Ned=6,游动次数Ns=4,迁徙概率Ped=0.3,最大评估次数FES=900000.对比算法的参数设置均参照文献[19]. 算法BFO、PDBFO、BBBFO的数值统计结果见表1,该统计结果包括30次独立运行最终结果的最优值Min、平均值Mean、标准差Std,三个指标中最优结果用黑体表示. 表1 3种算法数值实验结果统计 从表1直观来看,(1)在10个测试函数中BFO、PDBFO和BBBFO在30次最终结果统计的最优值上分别有1个、2个和7个最优结果;(2)BFO、PDBFO、BBBFO在10个测试函数上最终结果统计在平均值上分别有0个、0个、10个最优结果;(3)BFO、PDBFO、BBBFO在10个测试函数上最终结果统计在标准差上分别有4个、0个、6个最优结果. 因此综合表1结果和相应分析可以看出,在CEC2014的测试函数上BBBFO得到的3个指标结果均有明显的优势,最优值和平均值统计结果也比BFO和PDBFO表现的更好. 为了考察新算法的收敛速度和综合在线性能,图1给出了3种算法经过30次运行得出每一次迭代的平均适应值对应的收敛曲线图,其中横坐标是函数值计算次数,纵坐标是30次独立运行中每一个进化代的平均适应值.选取代表性收敛图,单峰函数F1、F2,多峰函数F3、F4、F5、F7,混合函数F8、F9. 图1 3种算法收敛曲线图 对比3个算法在求解CEC2014测试函数的收敛性能,(1)BBBFO收敛速度明显优于BFO和PDBFO;(2)对于多峰函数,BBBFO在F3、F4上的收敛速度和精度远优于其他两种算法,在F5、F7略优于其他算法,可以分析出当求解多峰函数时BBBFO的性能比其他算法优势较明显;(3)在求解单峰函数时,BBBFO收敛优势不太显著,但后期放大来看BBBFO仍然优于其他算法;(4)在求解混合函数时,BBBFO算法也具有较为明显的竞争优势.总之,在这些复杂函数优化上的综合性能表现,本文提出的BBBFO算法表现出优异的优化性能和潜力. 为进一步考查3种算法在多次运行最终结果中的离散程度,图2给出了3种算法经过30次运行得出最优结果的箱型图,箱型图中横坐标为3个算法,纵坐标为函数适应值,其中5条线从上到下分别为:最大值、上四分位数、中位数、 下四分位数和最小值,同样选择函数F1、F2、F3、F4、F5、F7、F8、F9为代表. 图2 3种算法最终结果箱型图 从图2来看,(1)在中位数上,BFO、PDBFO和BBBFO分别取得0个、1个、7个最优结果;(2)从上下四分位距上来看,BFO、PDBFO和BBBFO分别取得4个、1个、3个;(3)对于多峰函数和混合函数,BBBFO在F3、F4、F5、F7、F8和F9上的中位数与其他算法的中位数值相差较大,可以看出在求解多峰函数和混合函数时BBBFO的性能显著优于其他两种算法. 综合可以看出,本文提出的算法BBBFO中位数结果最优,因此新算法具有较好的性能表现,且具有较好的稳定性和鲁棒性,特别针对多峰函数和混合函数的复杂优化问题上具有较为明显的优势. 本文受骨干算法的启发,充分利用算法中骨干思想的优质解邻域随机生成新解的策略,在繁殖操作中引入基于动态高斯变异的骨干操作,在保持精英邻域搜索的基础上增加了种群多样性,提高了求解精度.另外趋化操作是细菌觅食算法的核心操作,其中游动步长是趋化操作中具有重要影响的一个,将固定的游动步长通过自适应改进,使得算法在前期搜索范围广、后期逐渐缩小搜索范围,这样使得算法在求解问题时的不同阶段对全局和局部搜索有所偏重,总体保持平衡.选用CEC2014基准测试函数,对本文提出的基于骨干思想的自适应细菌觅食优化算法与同类算法进行对比仿真实验,结果表明本文提出的算法总体性能更好,具有更好的收敛速度和精度,并且具有良好的稳定性和鲁棒性. 对于细菌觅食优化算法的研究还有许多问题,我们可以尝试将贪婪替换或竞技搜索引入算法中,还可以将本文的新思想与其他智能算法相结合.2 骨干粒子群算法
3 基于骨干思想的自适应细菌觅食优化算法
3.1 自适应步长
3.2 基于骨干思想的BFO
3.3 算法流程
4 仿真实验与结果分析
4.1 测试函数与参数设置
4.2 实验数据对比
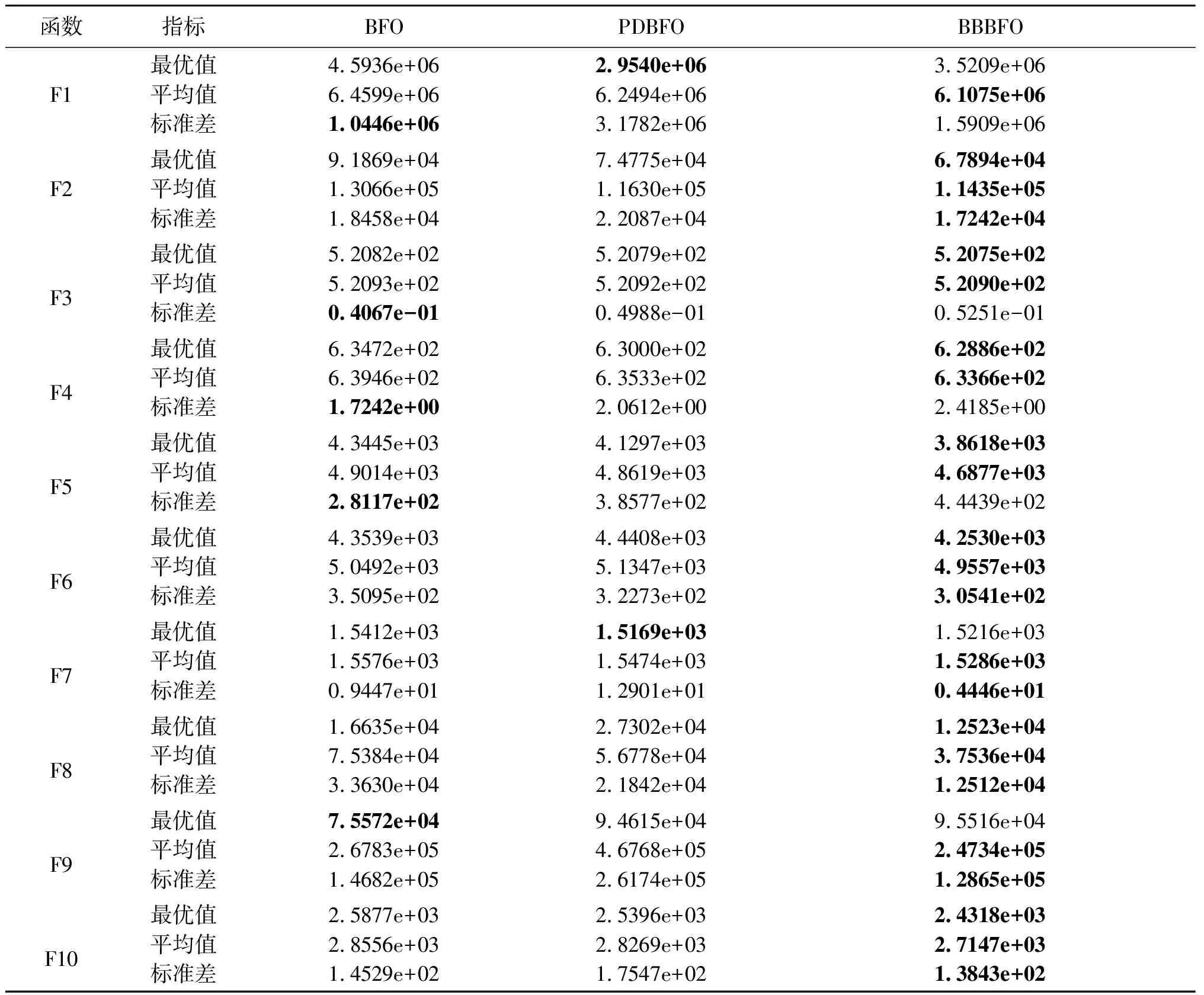
4.3 收敛速度对比分析
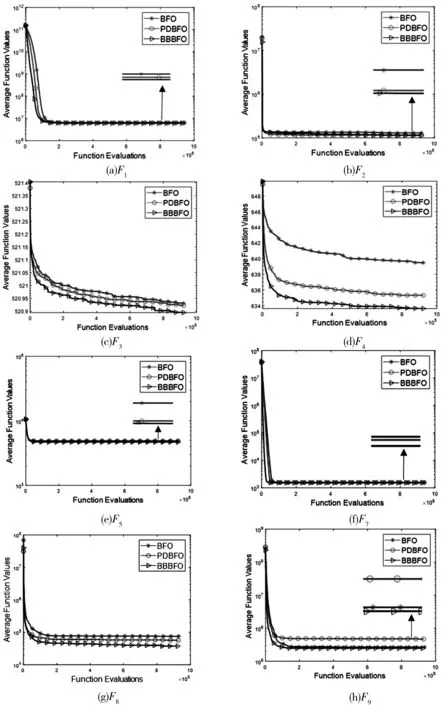
4.4 最终结果离散度对比
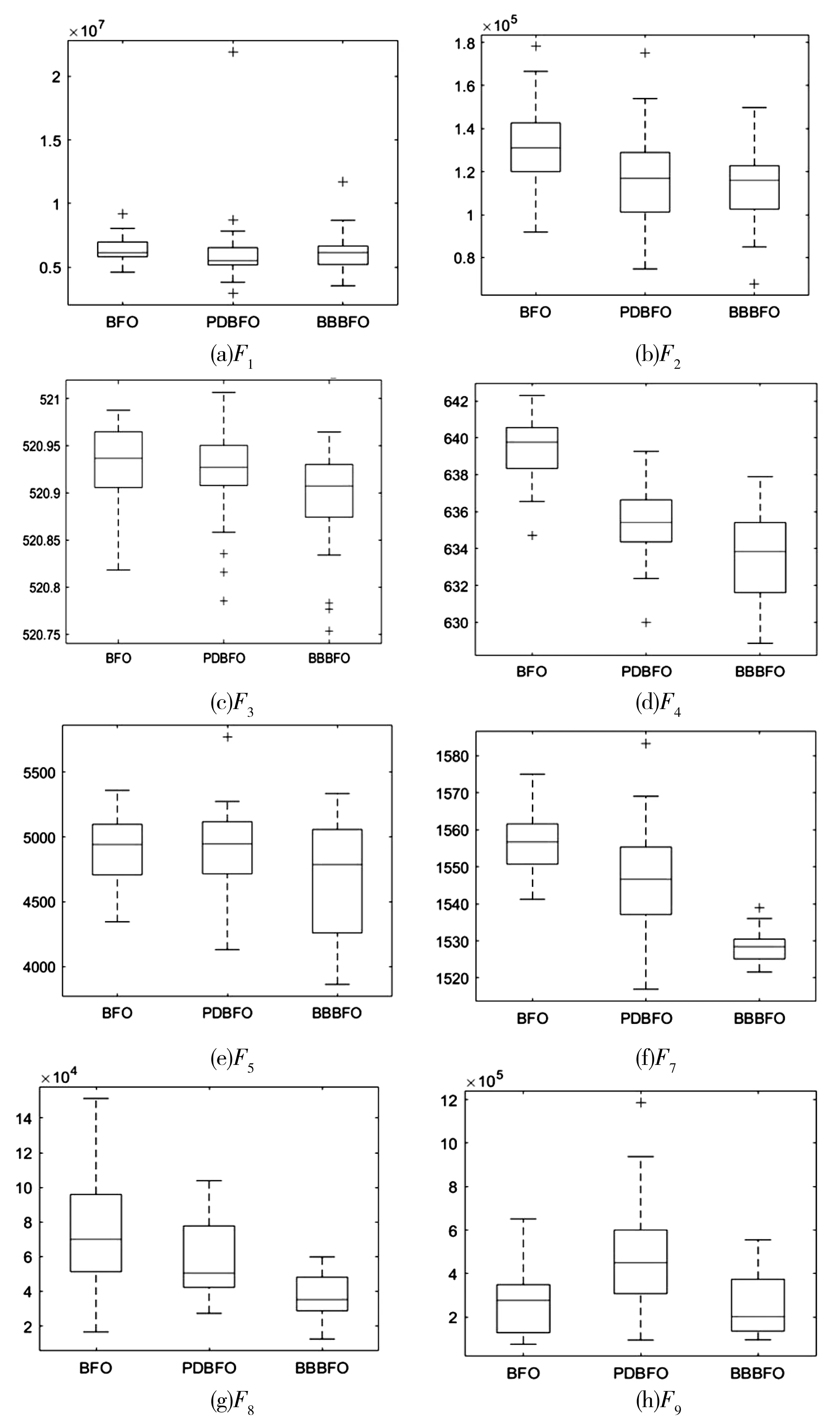
5 结 论
