基于去噪自编码器网络特征降维与改进小批优化K均值算法的海量用户用电行为聚类及分析

2022-06-15肖先勇

电力自动化设备 2022年6期

汪颖，杨维，肖先勇，张姝

（四川大学电气工程学院，四川成都 610065）

0 引言

随着我国清洁能源渗透率的不断提高以及新型负荷增长速度的不断加快，用户侧的用电监测与调控愈发重要［1-2］。随着配电网高级量测体系AMI（Advanced Metering Infrastructure）的持续推进与建设，用户用电信息测量、存储、分析与应用的完整体系被构建，这使得基于电力大数据分析来实现用户侧用电调控成为可能。准确进行用户用电行为聚类分析与用户画像是开展用电调控的必要前提，可为优化峰谷差、平衡供需缺口提供数据支撑，并且根据用户画像的结果可明确用户的用电需求与价值，这是进行用户细分、实施精准营销的基础。

用于用户用电行为挖掘与分析的技术主要包括非侵入式负荷监测NILM（Non-Intrusive Load Moni‐toring）技术和大数据驱动的负荷聚类技术［3-4］。前者通过对用户总线数据的监测与分解，实现各用电设备投切与运行的监测，实时分析用户的用电行为，对该技术的研究较为成熟，但该技术属于设备级的监测技术，受监测终端改进、用户隐私等问题局限，尚未广泛应用。后者是典型的无监督式机器学习的应用，属于用户群的监测技术，适用于分布广泛的海量用户数据的实时分析。

近年来，随着国家电网公司不断推进配电网的智能化和自动化，各类监测终端与计量装置被广泛应用，形成了营销系统、计量系统、配电网自动化系统、配电网生产系统等，多源、海量的电力数据给数据挖掘与分析工作带来了巨大挑战。根据测算，我国智能监测终端每日生成几百亿条数据，每年产生的数据量超过70 TB［5］。在实际工程中，用电特性聚类的各项应用均面临着用户类型多样、体量庞大、数据通信制约等问题，如何高效地实现海量用户用电行为的挖掘与分析，是当前面临的重要问题。

针对上述问题，学者们主要从算法优化、大数据处理技术应用等方面开展研究。算法优化主要体现在数据降维以及聚类方法的选择与优化2 个方面。文献［6］定义用电行为指标，对负荷数据进行降维，提出基于聚类有效性修正的德尔菲法，对日负荷特性指标进行权重配置，并以加权欧氏距离为相似性判据，实现日负荷曲线的分类；文献［7］结合推土机距离EMD（Earth Mover’s Distance）和欧氏距离度量不同用户用电行为的差异程度，通过统计电力用户在多日同一时刻的负荷分布情况，从横向和纵向2 个角度全面表征用户的用电行为，提出一种考虑负荷纵向随机性的基于EMD 的用户用电行为识别新方法；文献［8］选取负荷曲线多维度特征，利用最大相关最小冗余mRMR（maximal Relevance and Minimal Redundancy）原则优选出特征子集，实现用户画像；文献［9］通过点积的方式构造核矩阵，将数据映射到高维空间中进行聚类，进而加大数据的可分性，并采用基于核方法的聚类算法提高负荷曲线聚类的准确性。

在大数据处理技术方面，Hadoop、Spark、Storm等大数据框架能有效解决海量数据存储、处理及分析等问题［5，10］，可将算法并行化，降低算法的时空复杂度。此外，分布式计算、云计算、边缘计算等为电力大数据分析提供了有效的解决方案。文献［11］将样本密度、类内样本平均距离的倒数和类间距离三者的乘积定义为权值积，以最大权值积法改进Kmeans 算法，以MapReduce 模型实现算法并行化，提高聚类的有效性与算法收敛速度。

传统的K-means 算法需要每个样本参与质心计算以及对所有候选中心计算相似度才能进行归类。当每次迭代都需要全体样本参与计算时，就会对硬件的存储、读写速度提出较高要求，无法实现有效的实时监测、分析与应用。为进一步提高计算效率，本文提出一种适用于海量用电数据分析的方法。首先，利用系统抽样方法从海量用户数据中筛选典型负荷数据样本，提取用户行为多维特征；其次，构建多层去噪自编码器DAE（Denoising AutoEncoder）模型，利用典型样本训练网络，实现特征优化与降维；然后，将小批优化K均值MBKM（Mini-BitchK-Means）算法作为聚类算法，通过优化质心选择与超参数优化对算法进行改进，其中超参数优化是基于高斯过程的贝叶斯优化算法GPBOA（Gaussian Process for Bayesian Optimization Algorithm）通过构建轮廓系数Sil（Silhouette coefficient）指标与超参数之间的优化关系来实现的；最后，利用互信息筛选用户用电行为关键特征，分析各类用户的用电行为与特点，并应用爱尔兰智能电表计量数据验证所提方法的有效性。

1 用电行为特征提取与归一化处理

与工业负荷相比，居民及商业负荷的波动性更强，受工作时间、温度、季节、电价、用户心理等主客观因素影响较大，本文参考国内外文献［6，8，12-13］定义常用的用户用电行为特征，特征的定义与物理意义见附录A 表A1。用电行为特征是根据日负荷曲线计算得到的，本文提取的特征分为直观描述型指标（包括日最大负荷时刻、日最小负荷时刻以及峰谷相距时间3 个指标）与比值描述型指标（包括日最小负荷率、日峰谷差率、日负荷率、峰期负载率、谷期负载率以及平期负载率6 个指标）2 类，按照时间尺度可以从全天与峰、谷、平4 个角度对用电行为特征进行划分。

由于不同的用户用电属性差别较大，因此在特征降维前对特征进行归一化处理以提升模型的收敛速度与精度，本文采用零均值归一化，即：

式中：X为归一化处理后的样本数据；Xinit为原始特征样本数据；μ为所有样本数据的均值矩阵；σ为所有样本数据的标准差。处理后的样本数据服从均值为0、标准差为1的标准正态分布。

2 基于DAE网络的多维特征优化

特征选择与降维技术可去除冗余特征以及提取有效信息，本文通过构建DAE 网络来实现高维特征的优化，提升聚类速度与效果。

2.1 自动编码器的特征降维与重构

2.1.1 自动编码器基本原理

典型的特征降维方法包括特征选择［13］和特征变换。特征选择包括过滤式、包裹式与嵌入式3 种，其通过一定的规则选出分类或聚类特征，难以保留全局信息；特征变换包括线性方法和非线性方法，这2种方法保留全局特征的能力存在差异。

自动编码器AE（AutoEncoder）是一种无监督式的特征降维与特征表达方法，由编码器与解码器构成，是一种输入和训练目标相同的神经网络。AE 的参数通过重构损失训练得到，重构损失为：

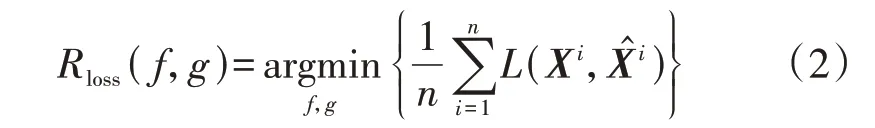
式中：Rloss(f，g)为重构损失，f为AE 的编码过程，g为AE 的解码过程；n为样本数，将每个样本的维度记为m，则X的大小为n×m；Xi为X的第i行，表示第i个样本；X̂i为第i个重构样本，所有重构样本构成X̂；argmin｛·｝表示获取特定AE 网络参数使得重构损失达到最小值。

AE的编码与重构过程r(X)表示为：

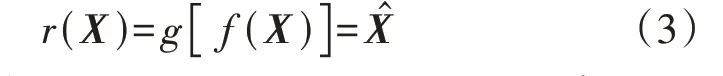
AE 的训练过程就是利用随机梯度下降法调整网络参数（权重w与偏置b），使重构信号与输入信号误差最小，本文选用交叉熵作为AE 的损失函数ξ(X)，即：

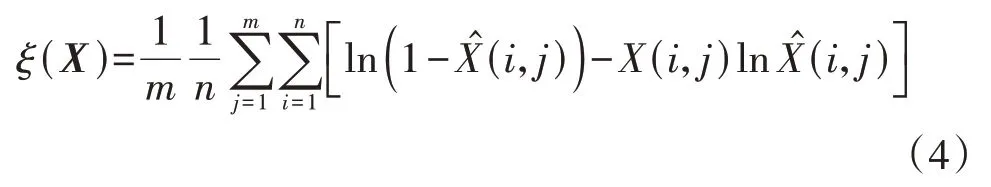
式中：X(i，j)为X的第i行第j列元素；X̂(i，j)为X̂的第i行第j列元素。

2.1.2 AE降维的维度约束

特征降维的目的主要有3 个：降低输入向量维度，从而降低聚类算法的复杂度；实现数据的可视化，以便于观察数据的分布特点；减轻数据传输压力，只需传递训练好的网络参数与降维后的数据即可实现数据重构。根据上述目的，特征压缩维度越低越好，但该维度受信息保留率［14］和信号重构误差限制，且信息保留率越高，信号重构误差越小。信息保留率η与重构损失函数eη分别为：

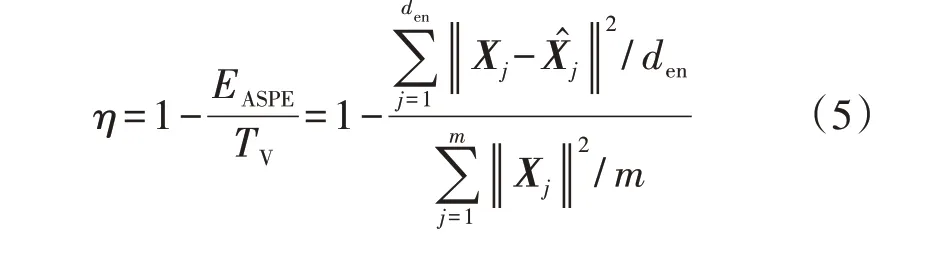
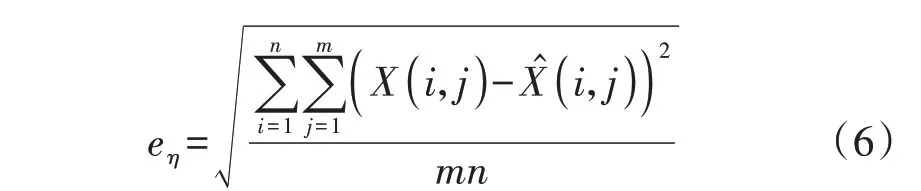
式中：EASPE为平均平方映射误差；TV为总变差；den为降维后的特征维度，其值根据η与eη的大小变化进行选取；Xj为X的第j列，表示第j维特征，X1—X9分别为附录A 表A1 中日峰谷差率、日最小负荷率、日负荷率、日最大负荷时刻、日最小负荷时刻、峰期负载率、谷期负载率、平期负载率、峰谷相距时间；X̂j为X̂的第j列，表示重构后的第j维特征。

2.2 DAE网络

传统AE 通过几十次迭代训练即可达到较好的效果，但易出现过拟合现象，通过随机失活（Dropout）正则化、增加输入样本噪声［15］等方法可提高模型泛化能力，因此，本文对训练样本增加噪声，如式（7）所示，在输入层间进行Dropout 处理，并在训练阶段减弱神经元的联合适应性，增强模型的泛化能力。

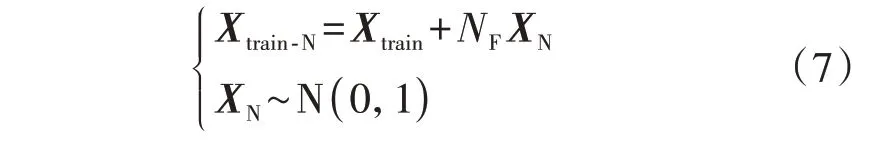
式中：Xtrain为训练样本；Xtrain-N为Xtrain通过式（7）产生的损坏数据；NF为噪声因子；XN为服从均值为0、标准差为1的正态分布的数据。

2.3 基于DAE网络降维的特征互信息分析

DAE 网络降维后的特征与初始特征不同，本文通过计算降维前、后特征的互信息MI（Mutual Infor‐mation）得到用户行为的关键特征，如式（8）所示。

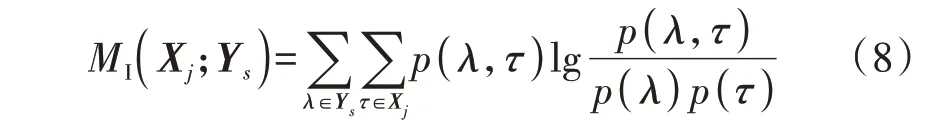
式中：Ys(s=1，2)为降至2 维后AE 的特征，表示Y的第s列；MI(Xj；Ys)为降维前、后特征的互信息；λ∈Ys、τ∈Xj表示λ、τ分别为Ys、Xj的元素；p(λ，τ)为λ和τ的联合分布概率；p(λ)、p(τ)分别为λ和τ的概率密度。互信息值越大表示两变量相关性越高；互信息值为0时，表示两变量相互独立。

3 基于改进MBKM算法的海量用电数据聚类

3.1 MBKM算法原理

聚类属于无监督学习范畴，是将无标签的数据按照同属性进行聚合。常见的聚类算法包括基于划分的算法、基于密度的算法、基于层次的算法、基于网络的算法和基于模型的算法五大类。K-means 算法是典型的基于划分的算法，该算法计算过程简单，时间复杂度低，但其对初始值的设置较为敏感，不能识别非球形类，并且当聚类样本量非常大时，即使考虑了距离优化，算法仍然较为耗时，且聚类效果不佳。在大数据背景下，文献［16］提出MBKM 算法以解决大样本聚类问题，该算法使用小批量样本优化K-means 算法［17］，即每次采用随机产生的子集训练算法，以缩短计算时间，该算法的优势在于小批量的随机噪声往往比整体的低［16］，当数据集随着冗余样本的增加而变大时，不会增加计算成本。

MBKM 算法主要是通过取样本的流平均值以及之前分配给质心的所有样本来更新聚类质心，达到降低聚类质心变化率的效果，如式（9）所示。

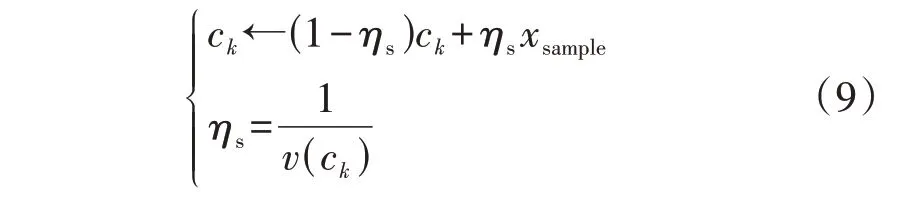
式中：ck(k=1，2，…)为第k个聚类质心；ηs为学习率；xsample为小样本中的一条数据；v(ck)为小样本第k个类的计数。在达到一定迭代次数后，小样本的收敛特性与整体样本收敛特性接近。

3.2 MBKM算法的改进

为进一步提升MBKM 算法的聚类速度和效果，本文从2 个方面对该算法进行改进：优选初始聚类质心；基于贝叶斯优化理论进行MBKM 算法初始超参数的优化。

在大数据背景下，K-means++算法［18］与本文改进MBKM 算法的效果相差极小，但是K-means++算法需要全部样本进行迭代，算法收敛时间会随着冗余样本的增加而增长。

3.2.1 初始聚类质心优化

本文在MBKM 算法的基础上，采用初始优化方法确定初始聚类质心，进一步提升算法的收敛性能。首先随机选取一个初始聚类质心，根据式（10）计算每个样本与已选出的聚类质心的最短距离De(Xi)，然后选取最短距离最大的点作为新的聚类质心，直到选出K个聚类质心，其中K为聚类数。

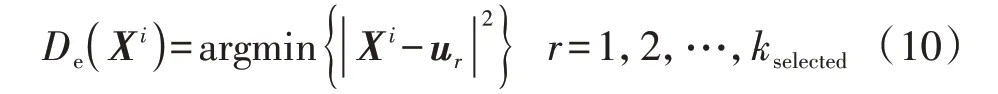
式中：ur为已选出的第r个聚类质心；kselected为已选出的聚类质心数。

3.2.2 基于高斯过程贝叶斯优化的超参数优化

超参数是独立于建模过程的自由参数，超参数优化可极大提升计算效率，常见的优化方法包括随机搜索、遗传优化等。在大数据背景下，上述方法的测试成本高，而贝叶斯优化根据已有测试数据决定下一次的测试参数，可大幅提高搜索效率。

MBKM 算法的主要参数见附录A 表A2。其中，初始化质心运行算法的次数Nt、质心被重新赋值的最大次数比例ε、连续采样包个数β决定了算法的整体运行时间，一般将Nt与β设置为默认值，对ε值进行寻优；采样包大小b默认值为100，如果发现数据集的类别较多或者噪声点较多，则对b值进行优化以提升聚类效果。本文选用Sil 作为MBKM 算法超参数（K、ε与b）的优化指标，K值通过肘部法则与Sil 变化曲线拐点综合确定［19］。肘部法则通过计算误差平方和SSE（the Sum of Squares due to Error）确定，即：

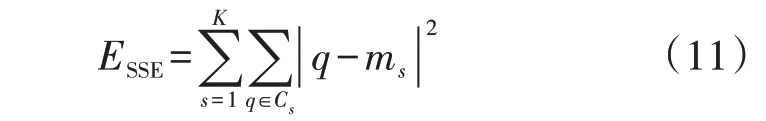
式中：ESSE为SSE；Cs为第s个类；q∈Cs表示q是第s个类的样本；ms为第s个类的聚类质心。

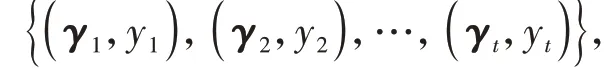
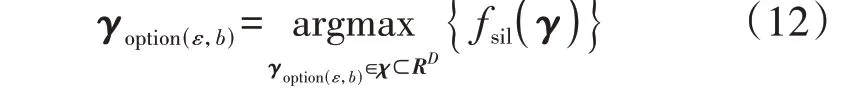
式中：γoption(ε，b)为待寻优超参数向量；χ为以ε与b为变量的超参数寻优空间；RD为以全体超参数为变量的寻优空间；argmax｛·｝表示最大值寻优过程；fsil(·)为超参数与Sil 的函数关系。GPBOA 主要包括以下3个步骤。

1）构建样本的高斯过程回归模型gD(γ，υ，Σ)，其中υ为均值矩阵，Σ为协方差矩阵。

2）求采样函数u(γ，gD(γ，υ，Σ)) 的极值点γ∗，即：

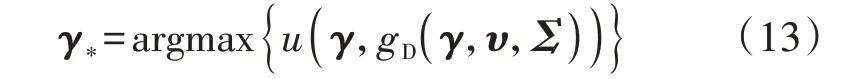
3）通过测试得到新样本(γ∗，y∗)，其中y∗=fsil(γ∗)+ε∗为新样本的观测值，fsil(γ∗)为新样本的估计值，ε∗为新样本的观测误差。更新总样本以及高斯过程回归模型，进入下一次迭代，依此循环，直至迭代结束。

步骤1）中的高斯模型是对给定样本估计出的概率分布，gD(γ，υ，Σ)服从如下多维正态分布：

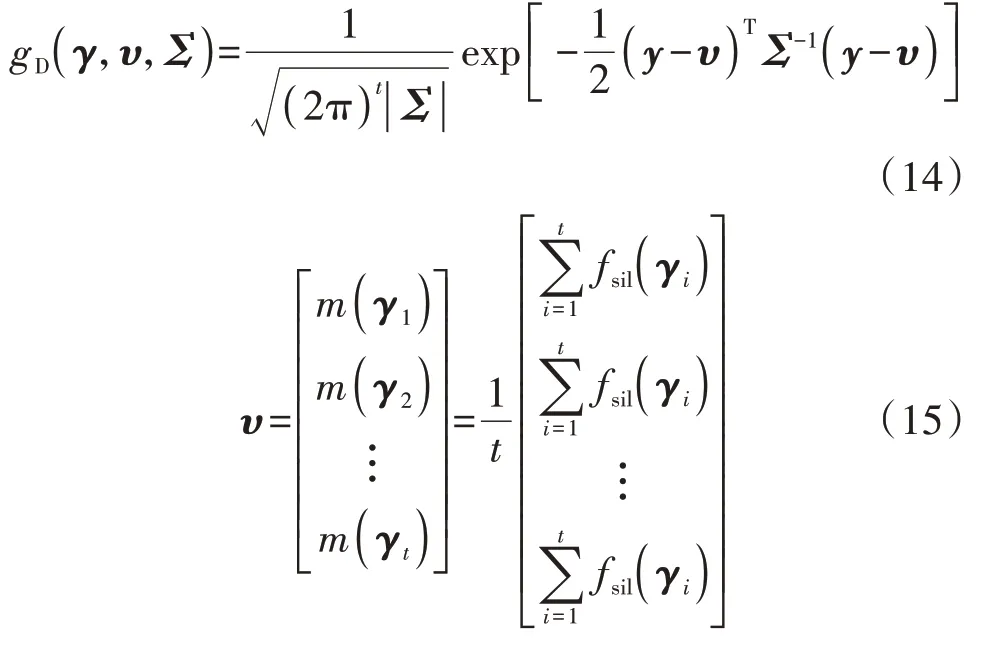
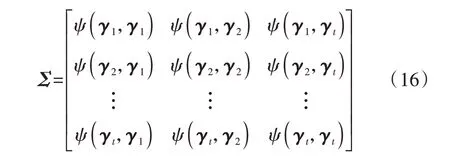
式中：m(⋅)为均值函数；fsil(γi)(i=1，2，…，t)为第i个样本的估计值；ψ( ⋅，⋅)为高斯核函数，本文选择平方指数SE（Squared Exponential）作为核函数。根据任意有限个随机变量都满足一个联合高斯分布的性质，并考虑观测值y的噪声误差，可得观测值y与超参数γ的边际似然分布ϑ(y|γ1，γ2，…，γt，)为：

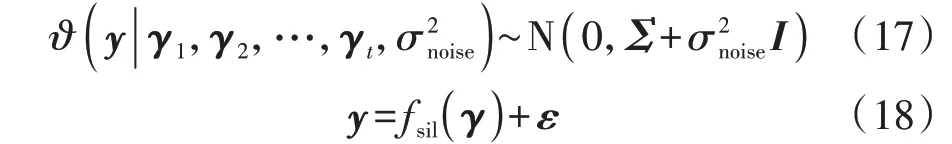
式中：ε为满足高斯独立同分布的噪声，噪声均值为0，标准差为σnoise；I为单位矩阵。当出现测试新样本(γ∗，y∗)时，根据样本观测值y与fsil(γ∗)的联合分布得到预测分布ϑ(fsil(γ*)|γ*，B1：t)为：

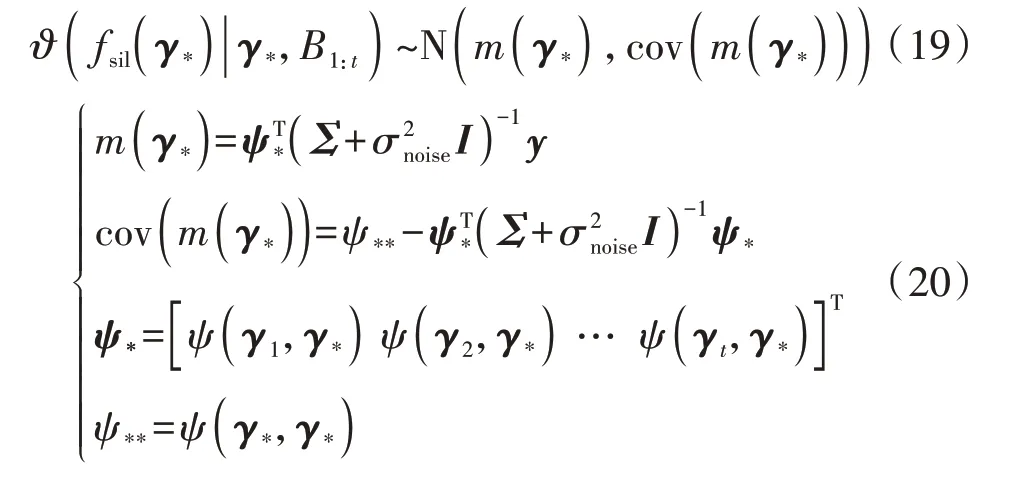
式中：m(γ*)为预测均值；cov(m(γ*))为预测协方差。

4 聚类有效性的评价指标

在实际工程中，大量数据是无标签的，常采用Sil、方差比标准指数CHI（Calinski-Harabaz Index）、邓恩指数DVI（Dunn Validity Index）、戴维森堡丁指数DBI（Davies-Bouldin Index）等［20］进行评价。本文选用Sil、CHI 及DBI 这3 类指数进行聚类有效性的评价。

第i个样本的Sil 值Isil(i)通过结合类内内聚度和类间分离度进行计算，即：

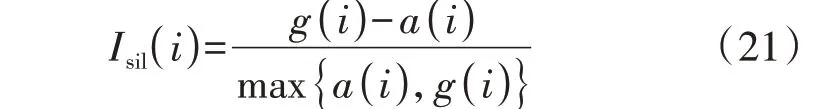
式中：a(i)为第i个样本的类内内聚度；g(i)为第i个样本的类间分离度。

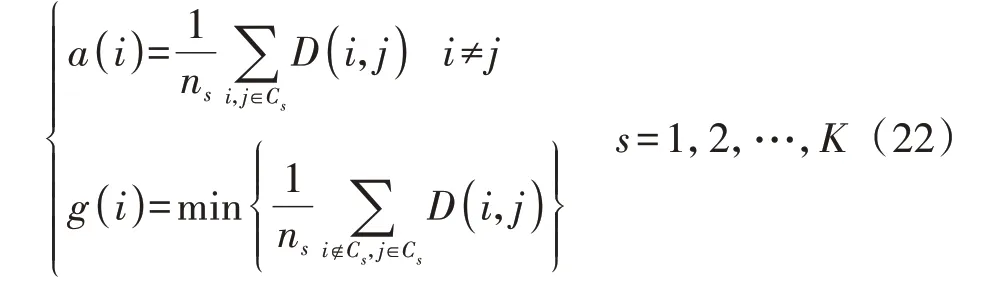
式中：ns为第s个类中样本的数量；D(i，j)为第i个样本与第j个样本之间的欧氏距离，表征不相似度。对所有样本的Sil值求平均值，以用于表示整体聚类效果，Sil值取值范围为［-1，1］，其越趋近于1表示类内内聚度和类间分离度越优。

CHI 是类间色散平均值与类内色散的比值，如式（23）所示，其值越大，则聚类效果越好。

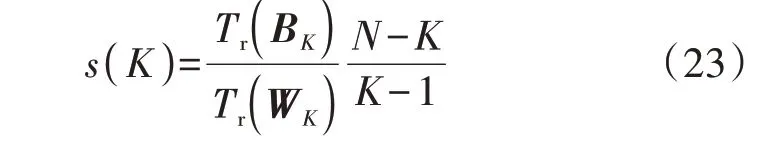
式中：s(K)为K个聚类数的总得分；Tr(⋅)为矩阵的迹；N为数据总数；BK为类间色散矩阵，WK为类内色散矩阵，两矩阵定义见文献［21］。CHI 的计算速度快，但凸类的CHI较高。

DBI是类内距离之和与类间距离之比，即：

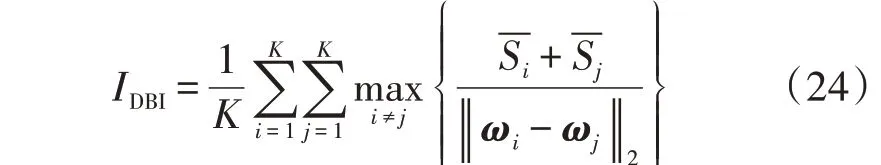
式中：IDBI为DBI分别为第i个和第j个类内数据到类质心的平均距离；ωi、ωj分别为第i个和第j个类的类向量，其欧氏距离表示类间距离。DBI 越小，则聚类效果越好。

5 本文方法流程

本文方法流程如图1 所示，主要包括典型样本训练、特征提取与预处理、DAE 网络特征降维、基于改进的MBKM算法聚类以及用户行为分析与画像。

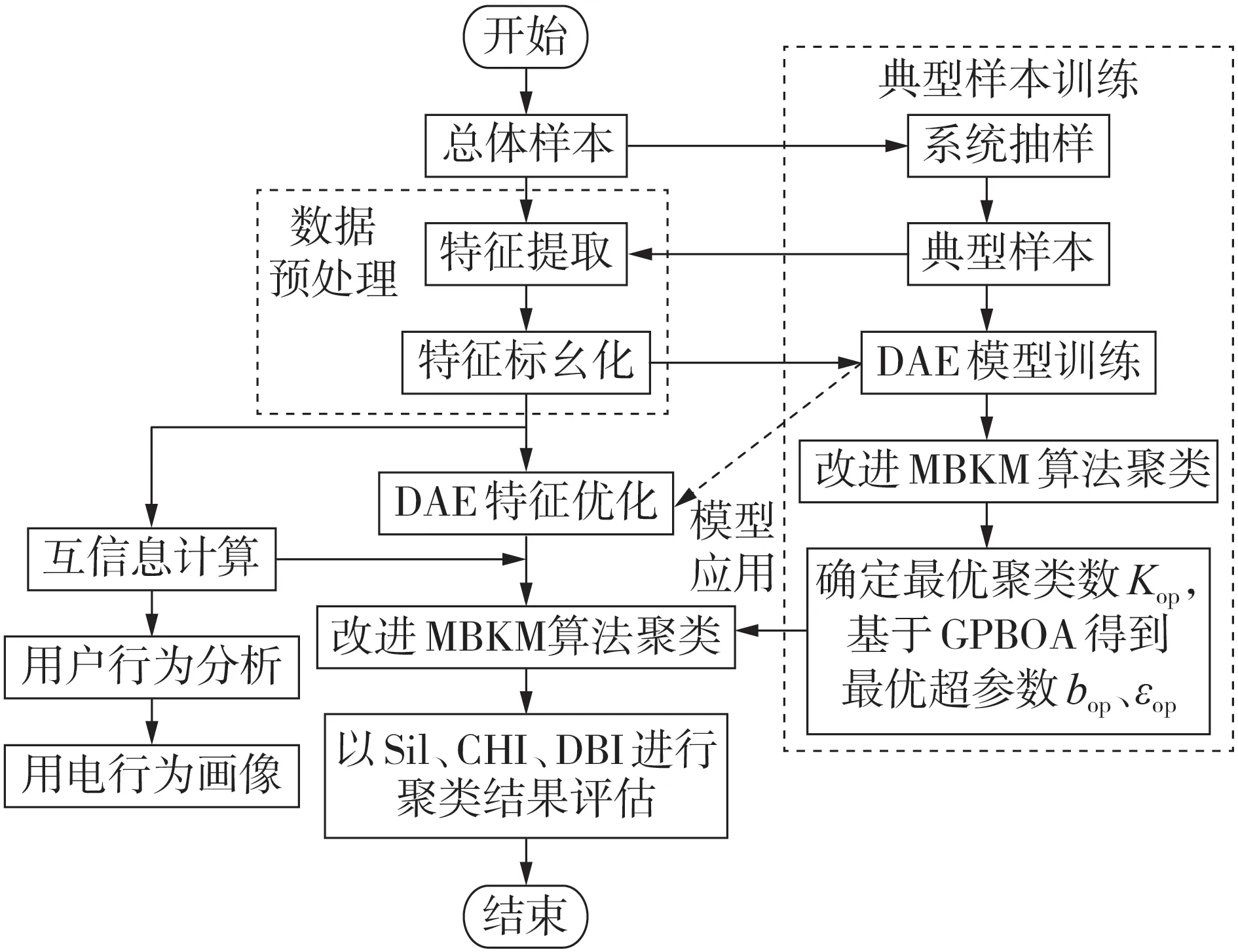
图1 本文方法流程图Fig.1 Flowchart of proposed method

典型样本训练是本文所提方法的基础，训练好DAE 模型应用于总体样本的特征优化后，本文采用系统抽样方法对典型样本进行抽取，即等距抽样。需要注意的是，在确定抽样方法前，需要校验样本的均衡性，当样本不均衡时，需要采取数据增强、分层抽样等策略。

6 算例分析

6.1 数据来源与实验平台

本文利用爱尔兰智能电表的计量数据［19］对所提方法进行验证，该数据来源于爱尔兰电力和天然气行业监管机构CER（Commission for Energy Regula‐tion）每隔半小时记录一次的用电量数据。实验硬件平台是64 位Windows 系统，该系统采用Intel core（i7），3.40 GHz 处理器，8 GB RAM。深度学习框架基于Keras（基于TensorFlow1.2）实现。

6.2 用户用电行为特征聚类

6.2.1 多层DAE网络的构建

本文随机抽取总样本的10%作为典型样本，共提取9 种用户用电行为特征，以用于训练网络。所构建的多层DAE网络参数见附录A表A3。网络共7层，采用全连接层，在全连接层Dense1与全连接层Dense2之间增加Dropout 正则化处理（神经元失活率为0.5）；从输入层到全连接层Dense3为编码结构，其将特征压缩至2 维；从全连接层Dense3到输出层为解码结构。网络训练共迭代200 次。图2 为DAE 网络训练误差曲线，由图可见，在迭代约30 次后DAE网络有效收敛。

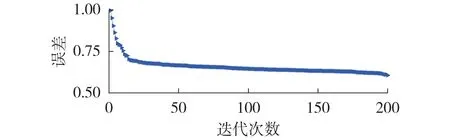
图2 DAE网络训练误差曲线Fig.2 Training error curve of DAE network

降维维度是通过不同数据压缩比例下数据的信号重构误差和信息保留率来确定的。当维度为2时，信号重构误差eη=0.86，信息保留率为90%；当维度为5 时，信号重构误差eη=0.82，信息保留率为95%。可见，维度降低并未损失过多信息，因此可令维度为2。

6.2.2 多层DAE网络的特征优化效果测试

为了证明所构建的DAE 网络的优化效果，本文从聚类指标、计算时长等方面对比本文所构建的多层DAE 网络、标准主成分分析PCA（Principal Com‐ponent Analysis）、截断奇异值分解TSVD（Truncated Singular Value Decomposition）、单层AE 以及多层AE的特征降维效果。

从数据集中随机抽取1 000 条用户数据作为测试样本，提取用电特征并将其维度降至2、采用Kmeans++算法进行聚类，结果对比如附录A 表A4 所示。由表可见：与未降维的结果相比，降维后聚类效果得到明显提升，计算时间明显缩短；本文方法与PCA 和TSVD 的计算时间相近，但聚类效果差别明显；单层AE以及多层AE的效果不如本文的多层DAE，这说明DAE的模型泛化能力较好。

6.2.3 基于改进MBKM算法与典型样本的超参数优化

本节对典型样本进行训练，利用训练完成的DAE 网络与改进MBKM 算法，以抽取的典型样本作为输入，确定全局样本最优聚类数Kop、改进MBKM算法最优超参数（εop与bop）。

选取典型训练样本，利用改进MBKM 算法得到图3，并进行最优聚类数Kop的判定。由图可见：当聚类数为2 和3 时，Sil 较大，当聚类数增至4 时，Sil 大幅下降，这说明聚类数增至4 之后聚类效果不佳；在聚类数增至3 后，SSE 减小的幅度变缓，这说明再增加聚类数的效果提升不明显，即聚类数为3 时是肘点。综上，可以确定最优聚类数Kop=3。

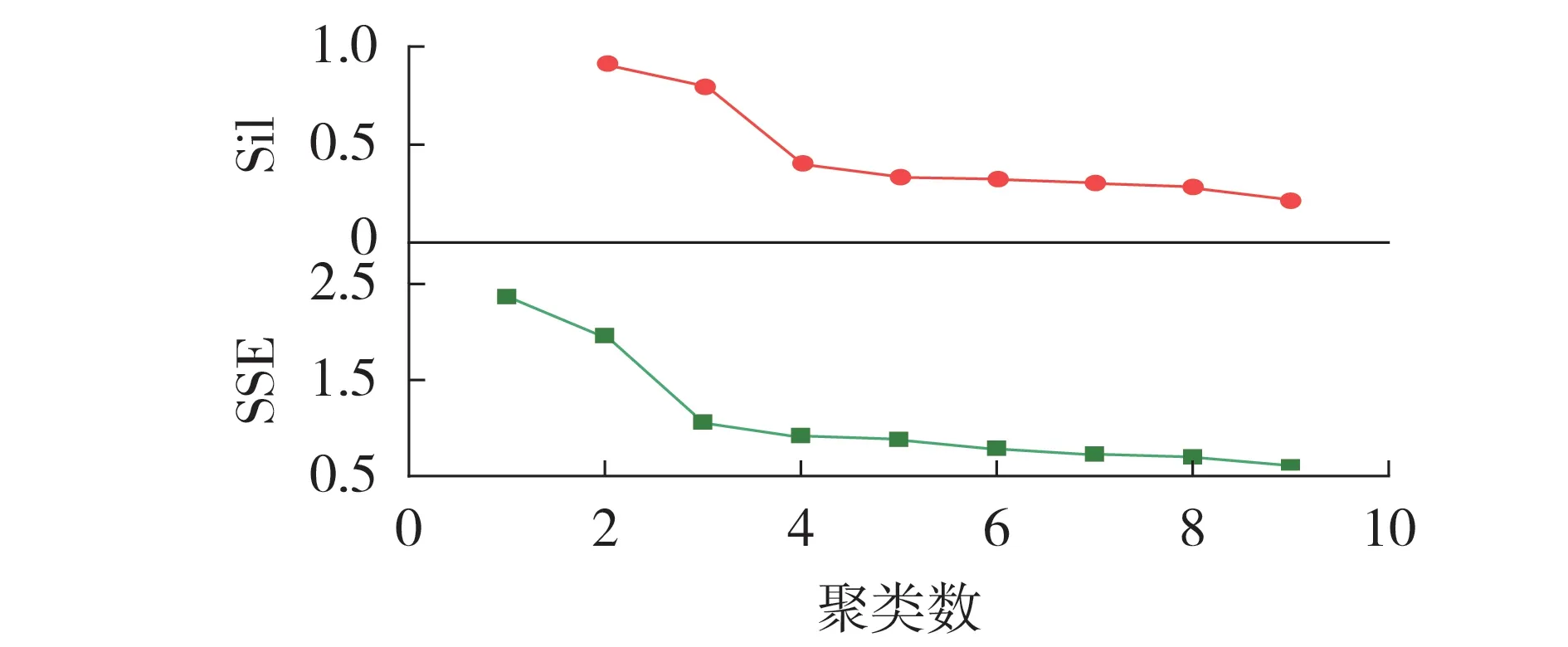
图3 聚类数与Sil、SSE的关系图Fig.3 Relationship diagram of clustering number vs. Sil and SSE

选取典型样本的用户数据作为超参数寻优样本，设置ε的取值范围为［0，0.04］，间隔为0.005；设置b的取值范围为［50，400］，间隔为50。附录A 图A1 为在ε与b初始测试样本下的Sil 分数热图，由图可见，不同的参数组合具有不同的聚类效果。设置GPBOA 的迭代次数为30，迭代过程中超参数与优化目标Sil 之间的对应关系如附录A 表A5 所示。由表可见，当迭代次数为24 时，Sil 出现最大值，迭代24 次之后的Sil呈现下降趋势，最终得到最优超参数bop=122、εop=0.03096。

6.2.4 聚类效果与计算时间对比

在不同数据集大小下，将改进MBKM 算法、传统MBKM 算法、K-means++算法、利用层次方法的平衡迭代规约和聚类BIRCH（Balanced Iterative Re‐ducing and Clustering using Hierarchies）算法、基于高斯混合模型的期望最大值聚类EM-GMM（Expected Maximum clustering based on Gaussian Mixture Model）算法、谱聚类SPC（SPectral Clustering）算法进行比较，各算法的聚类效果如附录A 表A6所示。不同算法的收敛时间如附录A 图A2 所示。由表A6 可知：BIRCH算法、K-means++算法、传统MBKM算法与改进MBKM 算法的聚类指标均明显优于EM-GMM算法与SPC 算法，其中K-means++算法、传统MBKM算法与改进MBKM 算法的效果优于BIRCH 算法；未经超参数优化与质心优化的传统MBKM 算法的聚类效果较差；相较于K-means++算法，以Sil指数为超参数优化目标的改进MBKM 算法的性能得到明显提升，不仅在聚类效果的整体指标上与K-means++算法十分接近，而且Sil指数更优。由图A2（a）可知，SPC算法收敛时间最长，呈现指数增长。由图A2（b）可知，数据集大小在0～10 000 范围内时，K-means++算法与改进MBKM 算法的收敛时间差别不大，但随着数据集继续扩大，K-means++算法的收敛时间增长明显，而改进MBKM 算法的收敛时间呈现缓慢的线性增长趋势，在分析更大的数据集时，改进MBKM算法的优势将更明显。

6.3 基于特征互信息计算的用电行为分析

本节应用所提方法对1 000 个不同用户在同一天的用电数据进行聚类。图4为经过DAE降维后的聚类情况，共分为3类用户，第1类用户的数量最多。

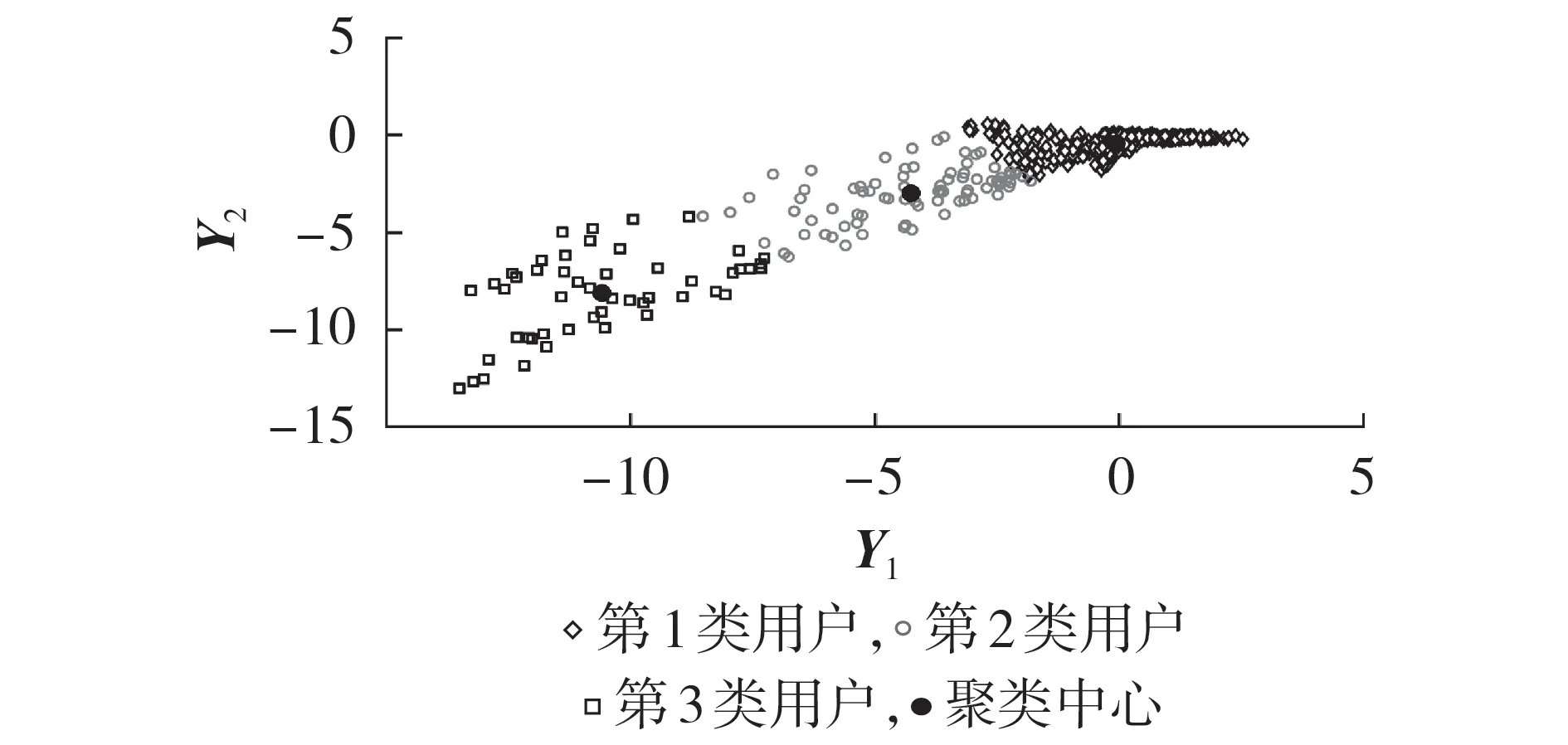
图4 降维特征的聚类结果Fig.4 Clustering results of dimension reduction features

聚类中心与行为特征的相关图如附录A 图A3所示。用户行为特征的互信息计算结果如表1 所示。由表可知：X1—X3与降维特征间的互信息相对较大，平均值在6以上；X4、X5、X7—X9与降维特征间的互信息相对较小，平均值在4以下。由图A3（a）可知，X1—X3与各类用户的统计值区分明显。综上可知，在初始特征空间中，X1—X3是主要分类特征。由图A3（b）可知，Y1与各类用户的统计值区分明显，而Y2与各类用户的统计值区分不明显。

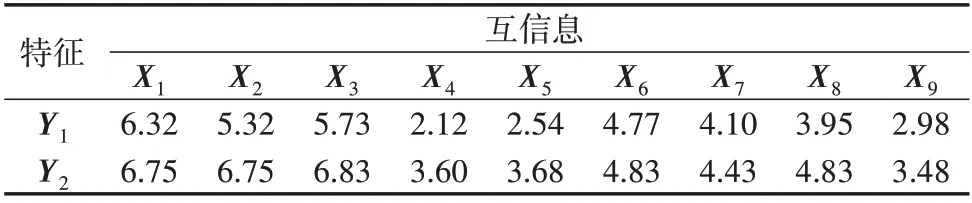
表1 初始特征与降维特征的互信息Table 1 Mutual information between initial features and dimension reduction features

3类用户的初始特征统计如附录A表A7所示，3类用户的用电属性特点如附录A 图A4 所示。第1类用户的X1—X3中心值与另外2 类用户的差别明显，第1 类用户的X1中心值为94.715 9%，约为第2类用户的4.8 倍，约为第3 类用户的1.7 倍；3 类用户的用电高峰约出现在11:00—14:00，这与降温负荷关系密切；第2类用户的峰谷相距时间为10.3793 h，第1 类与第3 类用户的负荷启停规律较相似。对比3 类用户的指标可知，不同类型用户在不同维度的用电特征上存在较大差异：第1 类用户用电波动最大，峰期负载率X6中心值最高，而谷期负载率X7中心值最低，这类用户多为商业等用户；第2 类用户的用电最平稳，多为轻工业等用户；第3 类用户的负荷有一定的波动性，整体负载率也较高，这类用户多为居民用户。