一种基于简化时域方程的LLC谐振变换器参数设计方法
2022-06-15牛靖凯吴学智赵宇明童亦斌辛晓敏
牛靖凯,吴学智,赵宇明,荆 龙,童亦斌,辛晓敏
(1. 北京交通大学 电气工程学院,北京 100044;2. 深圳供电局有限公司,广东 深圳 518020)
0 引言
随着宽禁带器件的不断发展,高频化和高功率密度成为了开关电源的发展方向,而LLC 谐振变换器凭借着结构简单、电磁干扰小、软开关等特点成为了隔离型开关电源的研究热点[1-3]。LLC 谐振变换器的参数设计主要围绕谐振腔展开,包含谐振电感、励磁电感和谐振电容3 个谐振参数,是变换器的增益、损耗、体积等特性的主要影响因素。当负载和开关频率发生变化时,LLC 谐振变换器的工作状态会发生改变,从而极大地增加了其谐振参数的设计难度。
目前,谐振回路参数设计方法主要可以分为基波分析法FHA(Fundamental Harmonic Approxima‐tion)、时域分析法TDA(Time Domain Analysis)以及FHA与TDA相结合3类。FHA以开关频率作为基波频率,通过分析LLC谐振变换器中的基波成分,建立交流等效电路,可以获取电压增益的数学表达式。FHA的优点在于可快速获得谐振参数和负载变化对增益的影响关系,从而得到谐振参数明确的优化方向,但在非谐振频率点的精度较差,导致所得到的参数准确度较低。文献[4-5]基于FHA 均提出增大励磁电感有利于降低损耗的观点,并结合零电压开关ZVS(Zero Voltage Switching)的条件计算了励磁电感,但未考虑励磁电感对最大增益、谐振电容耐压的影响。文献[6]基于FHA 得到了直流增益、输入阻抗和关键点电流的公式,并利用混沌-布谷鸟搜索算法对励磁电感、谐振电感的取值进行了优化,但由于使用FHA 导致精度较低,且算法较为复杂。文献[7]基于FHA 分析谐振电容对关断损耗的影响,得出了减小谐振电容有利于降低关断损耗及缩小频率范围的结论,但其本质是在同一谐振频率及频率范围下,谐振电容减小,谐振电感和励磁电感增大,进而影响了关断损耗。文献[8]基于FHA 得到变量之间的矢量分析图,进而对谐振参数进行设计,其过程较为直观,但由于FHA 的精确度较差,设计结果精度较差,并需少量迭代。
TDA针对谐振过程的各个阶段建立详细的时域微分方程,并通过求解软件进行求解得到具体的时域函数。TDA 的优点在于所求得的结果精度高,缺点是计算复杂,难以分析参数之间的影响关系,因此一般常与FHA 相结合进行分析。通过将FHA 和TDA相结合,在一定程度上可提高分析精度,降低计算量。文献[9]通过将LLC谐振变换器在PO 模式下的波形进行简化后分析得到了增益公式,重点分析了该模式下的边界条件,但未利用该公式进行进一步的参数设计。文献[10]基于TDA 分析了谐振频率与励磁电感对谐振点损耗及效率的影响,指出较高的谐振频率和较大的励磁电感有助于降低损耗、提高效率,较大的励磁电感也会影响变换器的最大增益,但文中对最大增益的分析采用了精度较低的FHA,且未考虑谐振电容耐压的问题。文献[11]围绕LLC谐振变换器原边开关管的关断损耗进行了详细的时域分析,但在关断损耗的计算中利用FHA 得到增益公式,从而降低了一定的精度,同时采用粒子群优化算法进行优化求解则增加了计算复杂性。文献[12]基于FHA 在考虑最大增益的条件下求得了励磁电感的最大值,并利用时域计算对最大增益进行了校正,对励磁电感的最大值进行了进一步优化,但需要进行多次迭代。文献[13]指出了FHA 的局限性,在考虑变换器效率、变压器耦合系数的影响下利用Pspice 仿真提高了增益曲线的精度,且设计时还考虑了谐振电容的耐压,但该方法仅适用于验证谐振参数而不适用于设计。文献[14]根据时域分析得出一套无需迭代的参数设计方法,但其计算求解较为复杂,在考虑ZVS 时仅考虑了关断时刻谐振电流等于0 的情况,而该情况下不能实现ZVS,同时未考虑最大增益下的谐振电容电压峰值。
通过对以上文献进行分析总结可以发现:
1)增加励磁电感有利于降低LLC谐振变换器的损耗,但励磁电感的最大取值受最大增益、ZVS、最小开关频率和谐振电容耐压的影响,现有的分析不够全面;
2)FHA可以快速分析各参数对LLC谐振变换器的影响,但精度较低,通过结合TDA 和仿真进行验证或校正虽然可以提高精度但需要多次迭代;
3)直接采用TDA 的分析计算过程较为复杂,需要采用一定的近似与简化或结合FHA 得到的公式来减少计算量,因而精度得不到保证;
为了解决以上问题,本文基于精度较高的简化时域方程进行了分析,明确了谐振参数、增益、ZVS和谐振电容耐压之间的关系,在考虑了以上因素后,提出了一种LLC 谐振变换器参数设计方法,并通过仿真及实验进行了验证。
1 电感系数对LLC谐振变换器增益的影响
本文主要围绕如图1 所示的LLC 谐振变换器拓扑进行分析。图中:S1—S4为原边开关管;Cr为谐振电容;Lr为谐振电感;Lm为变压器励磁电感;变压器匝比为N∶1∶1;D1和D2为副边整流二极管;Co为输出滤波电容;Rload为负载电阻;Vi为输入电压源;Vo为输出电压;Vc为谐振电容上的电压;Ir为流过谐振电感的电流;Im为变压器励磁电流;ID1、ID2分别为流过D1和D2的电流;IRload为流过Rload的电流。
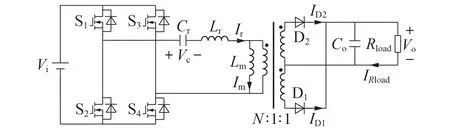
图1 LLC谐振变换器拓扑结构Fig.1 Topology structure of LLC resonant converter
当负载与开关频率不同时,LLC 谐振变换器的工作状态也不同,其时域分析也不同。为了简化分析过程,首先明确需要分析的工况,然后分析谐振参数对电压增益的影响。
1.1 运行工况分析
LLC 谐振变换器有3 个谐振元件,包含了2 个谐振频率:一个为Cr和Lr的谐振频率fr,另一个为Cr、Lr、Lm的谐振频率fm。通常,LLC 谐振变换器的开关频率fs>fm,原边开关管可实现ZVS,且变换器的增益随频率的增加而单调递减。
当fs=fr时,LLC 谐振变换器的增益将不受负载影响,始终等于变压器的变比,变换器的效率最高;当fs≠fr时,随着负载增大,LLC 谐振变换器的电压增益将减小。
当fs
根据文献[14]可知,在全负载范围内满足增益范围的需求可简化为如下2 个:①最高开关频率且空载条件下可以满足最小增益;②最低开关频率且满载条件下可以满足最大增益。
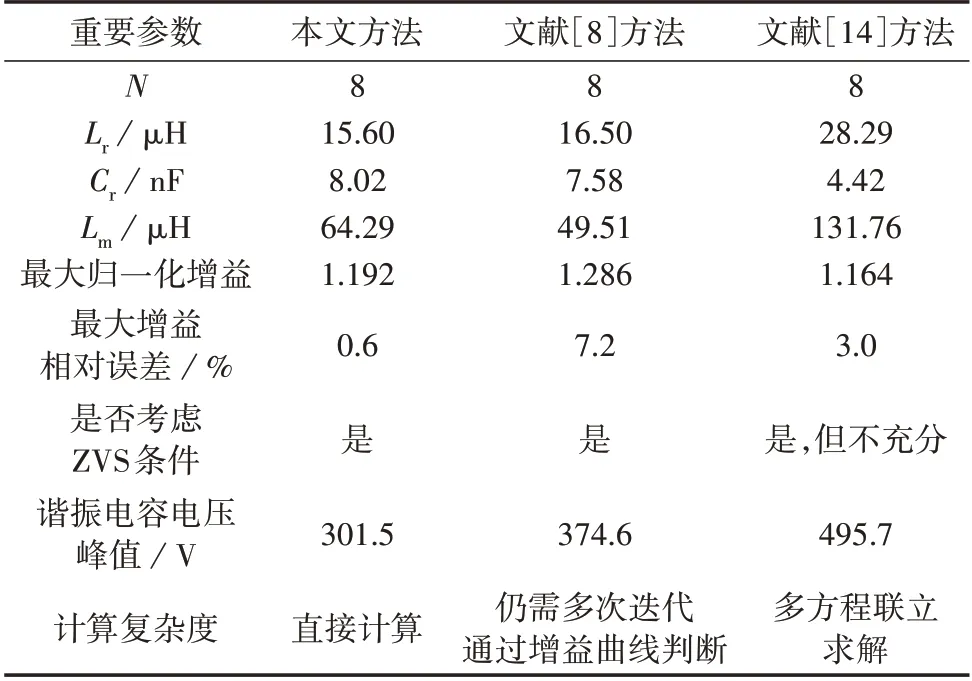
对于最小增益而言,其在采用移相控制、burst模式控制时易于实现,且基本不受负载和谐振参数的影响。对于最大增益而言,文献[17]指出通过增加一定的元件,可以拓展增益范围,从而达到更高的增益,但增加了元件成本和额外的损耗,适用于暂态升压,不适合稳态的参数设计。而在不对LLC 谐振变换器拓扑进行改动的情况下,只有通过合理的谐振参数设计才能在fs 因此,本文的重点研究工况为fs 一般fs越大,无源器件的容量和体积越小,变换器体积就可以越小。实际中,一般会根据所选控制器对开关频率的控制精度、开关管特性等条件,预先设定一个合适的开关频率范围(fs_min~fs_max,其中fs_max、fs_min分别为开关频率的最大值和最小值)作为设计指标。 由1.1 节的分析可知,为了减少fs>fr工况的使用,可根据输入电压范围(Vi_min~Vi_max,其中Vi_max、Vi_min分别为输入电压的最大值和最小值)和额定输出电压VoN,合理设置fr和N,即: 若需保证额定输入电压ViN工况下的效率最高,则可通过改变N保证额定工况在谐振频率下,而更小的增益通过移相控制、burst模式控制来实现。 在fs 图2 LLC谐振变换器的典型波形Fig.2 Typical waveforms of LLC resonant converter [0,t1)和[t1,t2]这2个模态下的时域表达式分别如式(3)和式(4)所示。 式中:Vc0、Vc1和Ir0、Ir1分别为0、t1时刻的谐振电容电压和谐振电感电流,由于波形具有对称性,t2时刻的电压、电流值为0 时刻的相反数;V′o为折算到原边的输出电压;Zr为谐振阻抗;Ln为电感系数;ωr为Lr和Cr的谐振角频率;ωm为Lr、Lm和Cr的谐振角频率。相关表达式如下: 根据稳态下Co上的电荷平衡可得: 根据文献[18]的方法,利用三角近似、对称性对式(3)、(4)、(10)进行化简,可得简化时域方程如下: 式中:Tk为t1与半个谐振周期的比例系数,其值接近1;Tn为归一化的开关周期。相关表达式如下: 由文献[18]可知,当fr和N确定时,谐振特性由Tn、Ln、Zr以及负载所决定。负载为设计需求,Tn为控制量,其范围由开关频率范围决定,则Ln和Zr共同决定了谐振参数。 根据波形特点,取Tk=1,并结合式(12)、(14)、(15),可得: 由式(20)可以看出,Tn与增益的近似关系主要与Ln有关,因此可利用开关频率范围和变换器增益范围来确定Ln,即: 在满足指标的条件下,Lm取得最大值将有利于降低变换器的损耗,Lm可表示为: 式中:Ln和fr在第1 节中已经确定,则Lm主要由Zr所决定,求Lm的最大值,即求Zr的最大值,而影响Zr最大值的因素主要有ZVS和谐振电容耐压。 虽然当fs>fm时具备实现ZVS 的条件,但ZVS 实现的本质是需要t2时刻的谐振电流在死区时间内将开关管输出电容上的电压减小到0,即需满足: 式中:Ir2为t2时刻的谐振电感电流;Coss为原边开关管的输出电容;tdead为死区时间。 忽略[t1,t2]时段谐振电流的变化,即认为Ir2=Ir1=-Ir0,结合Tk=1和式(14),可得Ir2的近似式为: Ir2与励磁电流峰值大小相近,而励磁电流最小且开关管输出电容电压最大发生在输入电压最大的工况下。当输入电压最大时,结合式(23)、(24),可得实现ZVS的约束条件为: 当fr为定值时,Zr越大,则Cr越小,流过相同Ir时的谐振电容电压峰值Vc_max越大。当LLC谐振变换器工作在fs_min且满载时,Im达到最大值,Ir也达到最大值,该工况下谐振电容的电压峰值发生在[0,t1)时段。 根据式(3),谐振电容的电压峰值可表示为: 根据谐振电容的成本、发热功率和选型确定其耐压,再考虑到为暂态过程保留一定的裕量,可预先设定稳态工作时的谐振电容电压峰值Vc_set。 式(26)包含了Ir0和Vc0这2 个变量,其中Ir0可用式(24)近似得到,Vc0可根据文献[18]的迭代公式得到,但过于复杂。考虑在理想条件下,在[0,t2]时段内,输入谐振网络的平均功率等于输出功率,即: 而[0,t2]刚好为半个开关周期,在此期间Vi为定值,且半个开关周期内对Ir的积分与谐振电容电压的变化量相关,同时考虑到波形的对称性,可得Vc0的近似式为: 将Ir0和Vc0的近似式代入式(26)中,可得约束式为: 式中:a、b、c为系数。 对式(29)进行分析可知,当c<0时,该不等式无解,该情况只在Vc_set设置不合理时发生。Vc_set需令c不小于0,即: 该不等式可化简为: 即稳态工作下谐振电容电压峰值不小于该值。因此式(34)可为谐振电容稳态工作的最小耐压提出设计依据,为谐振电容耐压等级的选型提供参考。 同时,当c不小于0 时,可知a>0,b<0,则式(29)可化简为: 通过式(35)可确定谐振电容耐压约束下的Zr最大值。 基于以上分析可知,经过工况分析和简化时域分析后,工作频段的选择、增益范围、ZVS 的实现、谐振电容电压峰值与谐振参数之间的关系变得更加清晰,具体如下:①最大开关频率决定谐振频率;②输入电压范围和输出电压范围决定变压器匝比;③最小开关频率和最大增益决定电感系数;④ZVS 与谐振电容耐压约束了谐振阻抗的最大值。 在此基础上,本文提出一种LLC 谐振变换器参数设计方法,为了补偿考虑死区时间、开关管导通压降和各类损耗对增益的影响,设计增益将在实际增益的基础上增加3%~5%。设计流程如下:首先,由式(1)确定fr,由式(2)确定N,由式(21)确定Ln;然后,根据式(25)、(35)确定Zr最大值;最后,由fr、Ln、Zr计算出Lr、Cr、Lm。 为了验证所提方法的有效性,本文将从3 个方面对该方法进行验证。首先,基于所提方法设计了一台如附录A 图A1所示的实验样机,将理论增益和实验结果进行对比,验证方法的准确性;其次,为了验证所提方法的适用性,通过改变设计指标,得到多组谐振参数,利用仿真对增益、谐振电容耐压等关键参数进行验证;最后,与采用频域分析但设计过程需要迭代的文献[8]方法以及采用时域分析且设计流程无需迭代的文献[14]方法进行了对比。 ZVS 约束的类似分析在很多文献中都有提及,为了重点验证本文所提的谐振电容耐压约束,实验采用了输出电容较小的开关管GS66508B,其ZVS 很容易实现,以减小ZVS约束的影响。同时,为了减小副边二极管压降和损耗的影响,使用2 个EPC2033开关管并联代替副边二极管,并使用同步整流芯片NCP4305A 进行同步整流。实验所使用的样机的设计指标与相关参数如附录A表A1所示。 为了更好地证明设计方法的精确性,在未适当增大所需增益的情况下,根据设计指标计算得到了谐振参数。实际使用的谐振元件参数存在一定的误差,如附录A 表A2 所示,表中谐振电感值为实际使用的谐振电感与变压器原边漏感之和。 利用理论数值进行时域仿真可以得到理论增益随频率变化的曲线,利用实际数值进行样机测试可以得到实验增益随频率变化的曲线,分别在额定负载和10%额定负载的轻载下进行了对比实验,对比结果如图3 所示。同时,为了进一步说明本文方法的精度较高,与基于FHA 的增益曲线进行对比。图中,曲线①、②分别表示所需最大、最小增益,后同。 图3 理论与实验的增益曲线对比Fig.3 Comparison of gain curves between theory and experiment 由图3可以看出: 1)在额定负载下,当开关频率为352 kHz 时,理论增益和实验增益的相对误差最大,约为3%,轻载下的最大增益则基本完全满足了最大增益的需求; 2)在轻载下,整体增益比额定增益略高,与1.1节中提到的满载下满足最大增益、空载下满足最小增益即可在全负载范围内满足增益需求的结论相符; 3)理论增益和实验增益的变化趋势相近,存在一个不随开关频率明显变化的误差,而基于FHA 的增益的变化趋势则与实验增益、仿真增益不同,其误差随开关频率偏离谐振频率的程度增大而增大; 4)理论增益与实验增益之间的误差主要是由分布参数、损耗、整流管的同步整流效果不理想等因素造成的。 为了进一步验证本文所提方法中时域分析的准确性,在最大增益及额定增益下的额定负载工况和10%额定负载的轻载工况下进行仿真和实验,得到输入谐振腔的电压Vin、Vc、Ir和输出电流Io的仿真及实验波形分别如附录A 图A2 和图4 所示。图中:Vin波形可反映开关驱动信号、输入电压等信息;Io波形结合负载电阻的大小可以反映输出电压。 从图4 中可以看出,额定负载实验下的谐振电容电压峰值接近300 V,与设计需求相符。额定负载和轻载下的实验波形均较为理想。输出电流波形存在的波动主要是由开关动作时产生的干扰导致的。 图4 不同工况下的实验波形Fig.4 Experimental waveforms under different working conditions 通过改变样机的输入电压范围、开关频率范围和谐振电容耐压,可以得到12 组谐振参数的组合,如表1所示。 表1 不同条件下的谐振参数Table 1 Resonance parameters under different conditions 利用表1 中的谐振参数与样机参数,通过数字仿真得到增益以及谐振电容电压峰值。由于轻载对增益曲线的影响可由4.1节得到,此处适用性验证仅选择本文主要研究的额定负载工况进行了仿真对比实验,在不同最小开关频率、不同最小输入电压和不同谐振电容电压峰值参数下利用本文所提方法的增益对比和谐振电容电压峰值对比,分别如图5和图6所示。 图5 不同谐振参数下的增益曲线对比Fig.5 Comparison of gain curves under different resonant parameters 图6 不同谐振参数下的谐振电容电压峰值Fig.6 Peak voltage of resonant capacitor under different resonant parameters 从图5(a)中可以看出,当增益范围不变时,随着开关频率范围变宽,本文所提方法的增益精度会有所下降;从图5(b)中可以看出,当频率范围不变时,随着增益范围的变窄,本文所提方法的增益精度会有所下降。结合图5(a)和图5(b)可以看出:①本文所提方法在不同系统需求条件下的增益误差均较小,具有一定的适用性,可以满足参数设计的需求;②结合所需的增益范围选择合适的开关频率范围可有效提高本文所提方法的增益精度。 从图5(c)中可以看出,谐振电容耐压的改变,即Zr的改变,对增益曲线的影响较小,进一步验证了开关频率范围与变换器增益范围主要由电感系数决定的结论。 从图6 中可以看出,12 组谐振参数下的谐振电容耐压参数基本都得到了满足,验证了所提方法在谐振电容耐压考虑上的有效性。 本文所提的参数设计方法是基于时域分析且无需迭代计算的。为了进行更有效的对比,分别选取了基于FHA 和基于TDA 的参数设计方法进行对比。基于FHA 的方法选择了设计过程较为直观的矢量法分析[8]。现有的基于TDA 的参数设计方法大多存在近似误差大、迭代计算复杂等问题[9-14],其中文献[14]是基于时域分析且无需迭代计算的参数设计方法,与本文类似,因此选择该方法与本文方法进行对比。 由于变压器、电感等制作工艺会影响损耗、增益等,进而影响2 种方法的对比,因此本文采用理想仿真来进行对比。在保证相同谐振频率、最小开关频率、变压器匝比且不考虑死区、磁性元件损耗等的理想仿真条件下,对本文以及文献[8]、[14]的参数设计方法进行最大增益误差、ZVS 实现、谐振电容电压峰值、计算难度的对比,结果如表2所示。 表2 不同方法的结果对比Table 2 Comparison of results among different methods 从表2 中可以看出:文献[8]的方法通过多次迭代观察增益曲线后,可以得到较为理想的谐振参数,但其最大增益误差较大,谐振电容电压峰值较高;文献[14]的方法可以基本满足增益的需求,但并未充分考虑ZVS 条件,具体体现在令开关动作时刻的谐振电流等于0,该工况下实际并不能实现ZVS,且其谐振电容峰值电压达到了输入电压2 倍以上,影响谐振电容的选型,增加了成本。同时,文献[14]的方法在求解时需要联立6~9 个含三角函数的方程组进行求解,较为复杂。与文献[8]、[14]的方法相比,本文所提方法在直接计算的条件下得到了与多次迭代相近、甚至更优的设计结果。 因此,利用本文所提的参数设计方法可较准确地满足设计指标要求。尽管由于分布参数、损耗等影响,实际增益略小于理论值,但可通过对增益最大值保留一个小的裕量来满足实际设计需求。 本文基于简化时域方程提出了一种LLC谐振变换器的谐振参数设计方法,该方法的主要特点如下: 1)明确了LLC谐振参数与变换器指标之间的关系,指出了电感系数主要决定了增益范围和开关频率范围,谐振阻抗受ZVS 条件和谐振电容电压峰值的约束; 2)不需要迭代即可实现参数的优化设计,计算过程简洁明确; 3)优化计算的准确度较高,可以满足LLC 谐振变换器的参数设计需求。 附录见本刊网络版(http://www.epae.cn)。1.2 工作频段的选择对谐振参数的影响


1.3 重点工况下的简化时域分析
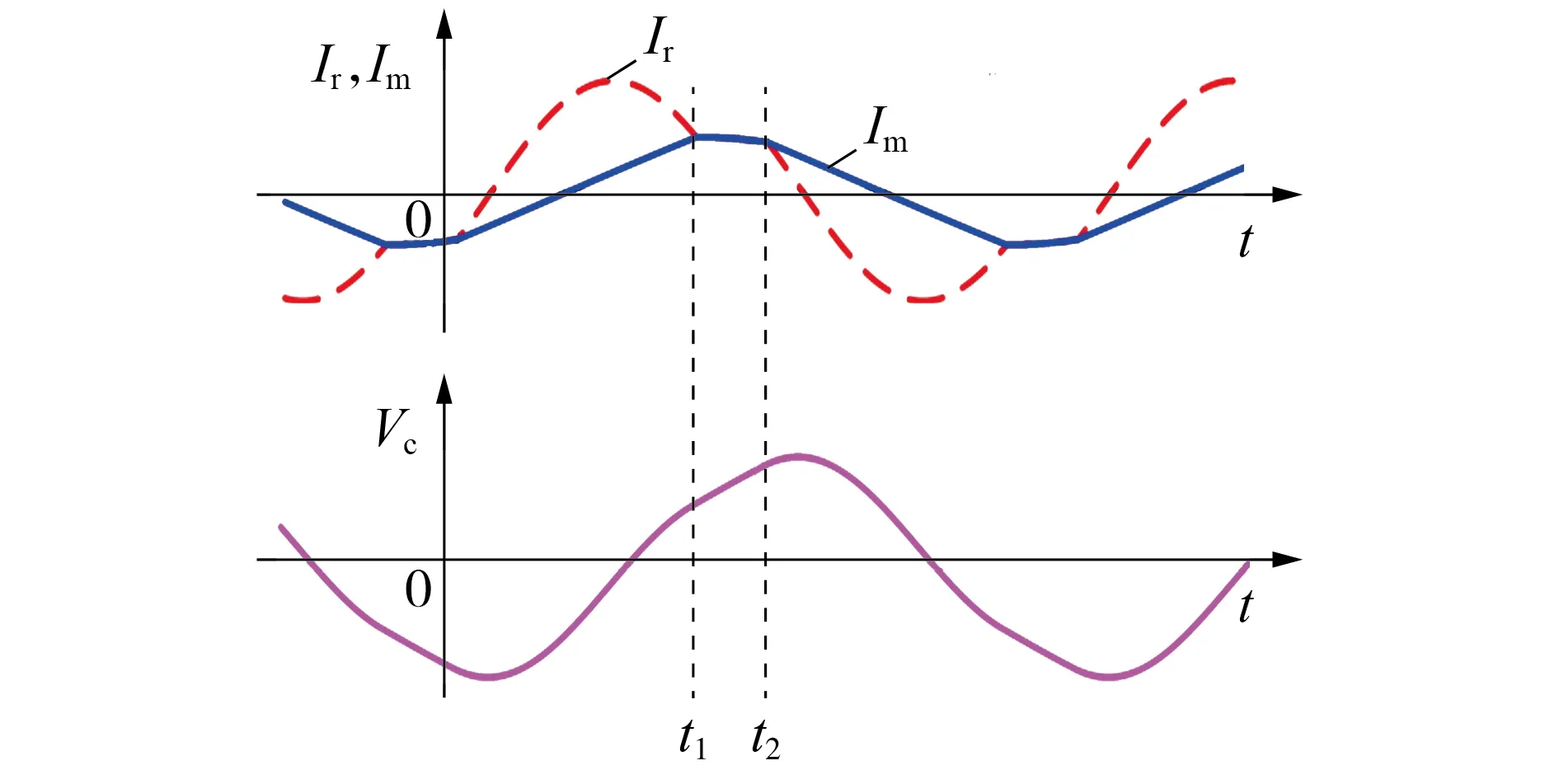
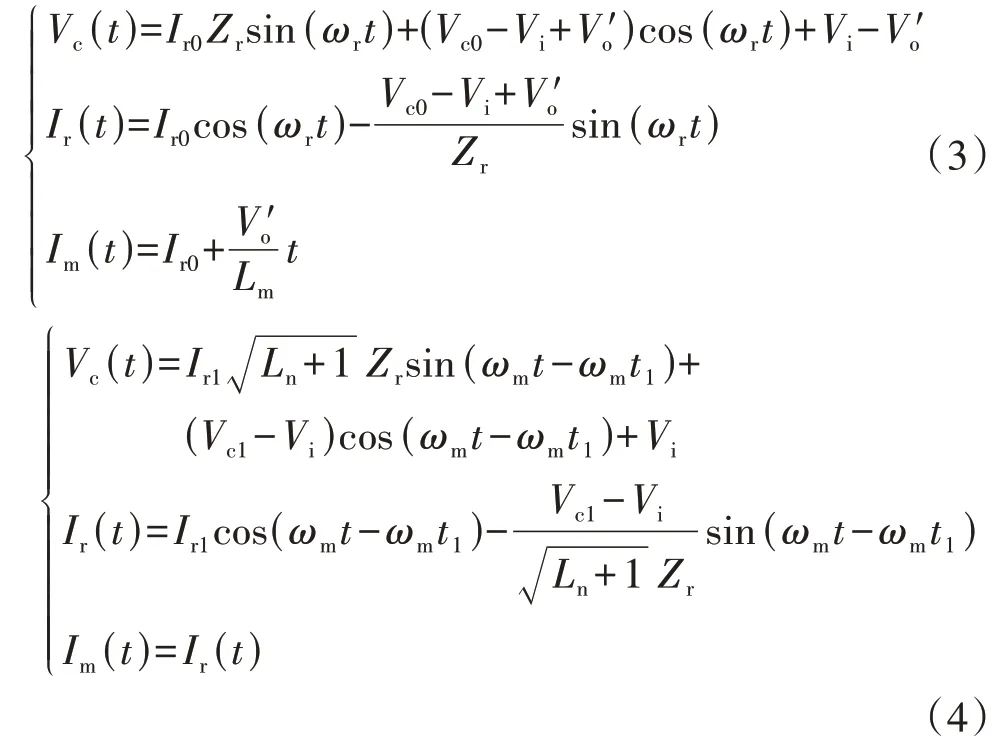
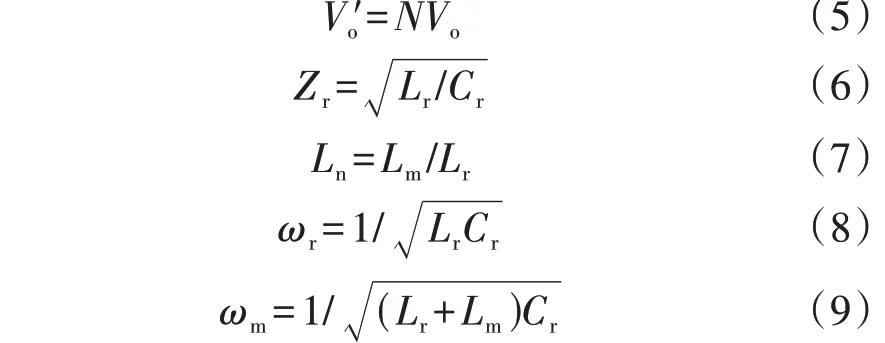
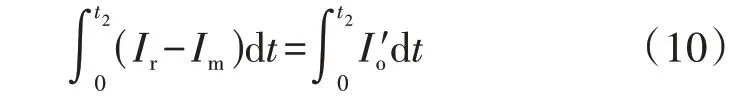

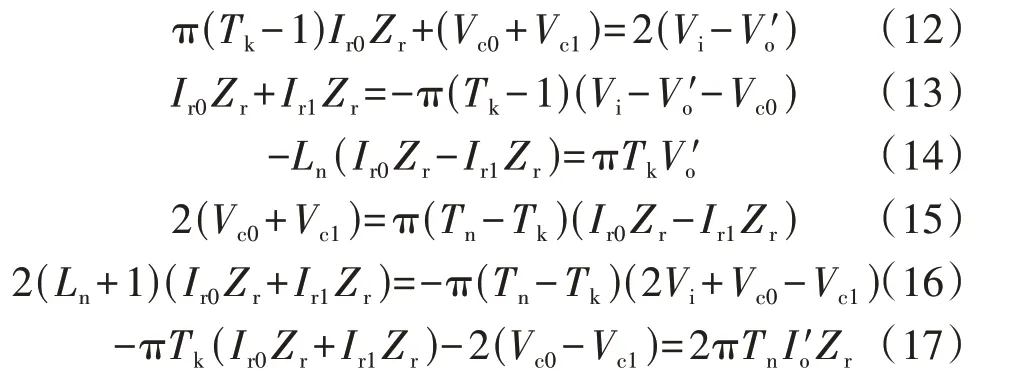
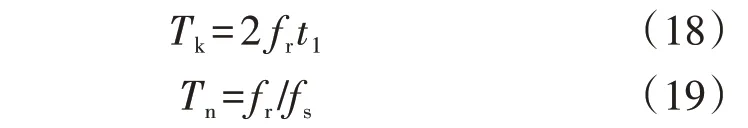
1.4 电感系数对增益范围的影响
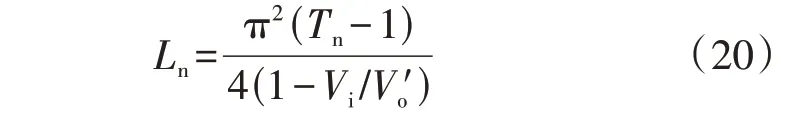
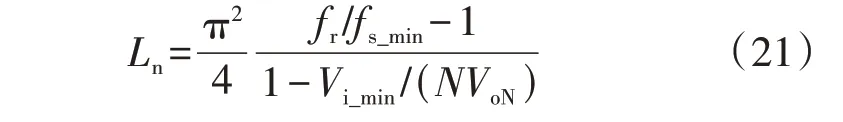
2 谐振阻抗的约束条件
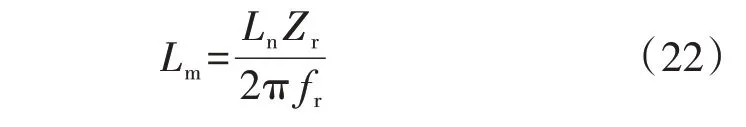
2.1 ZVS的约束条件

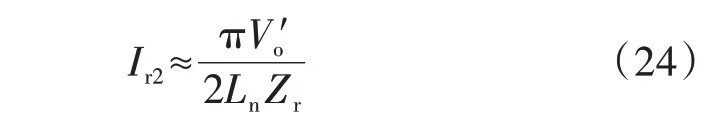
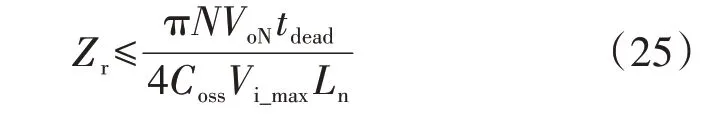
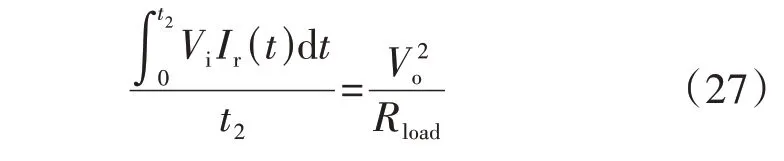
2.2 谐振电容耐压约束
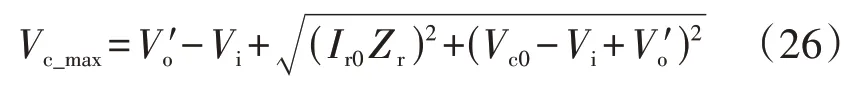
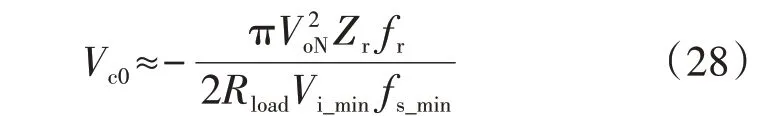
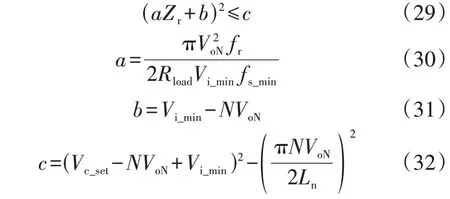
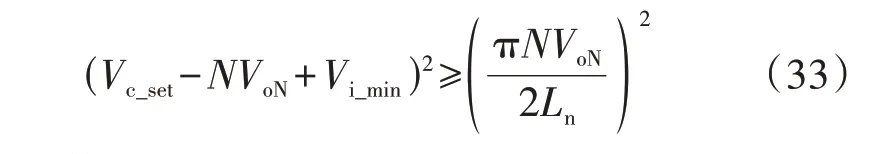
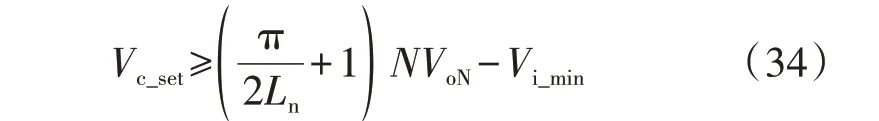
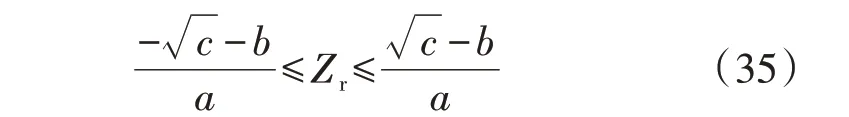
3 设计流程
4 方法验证
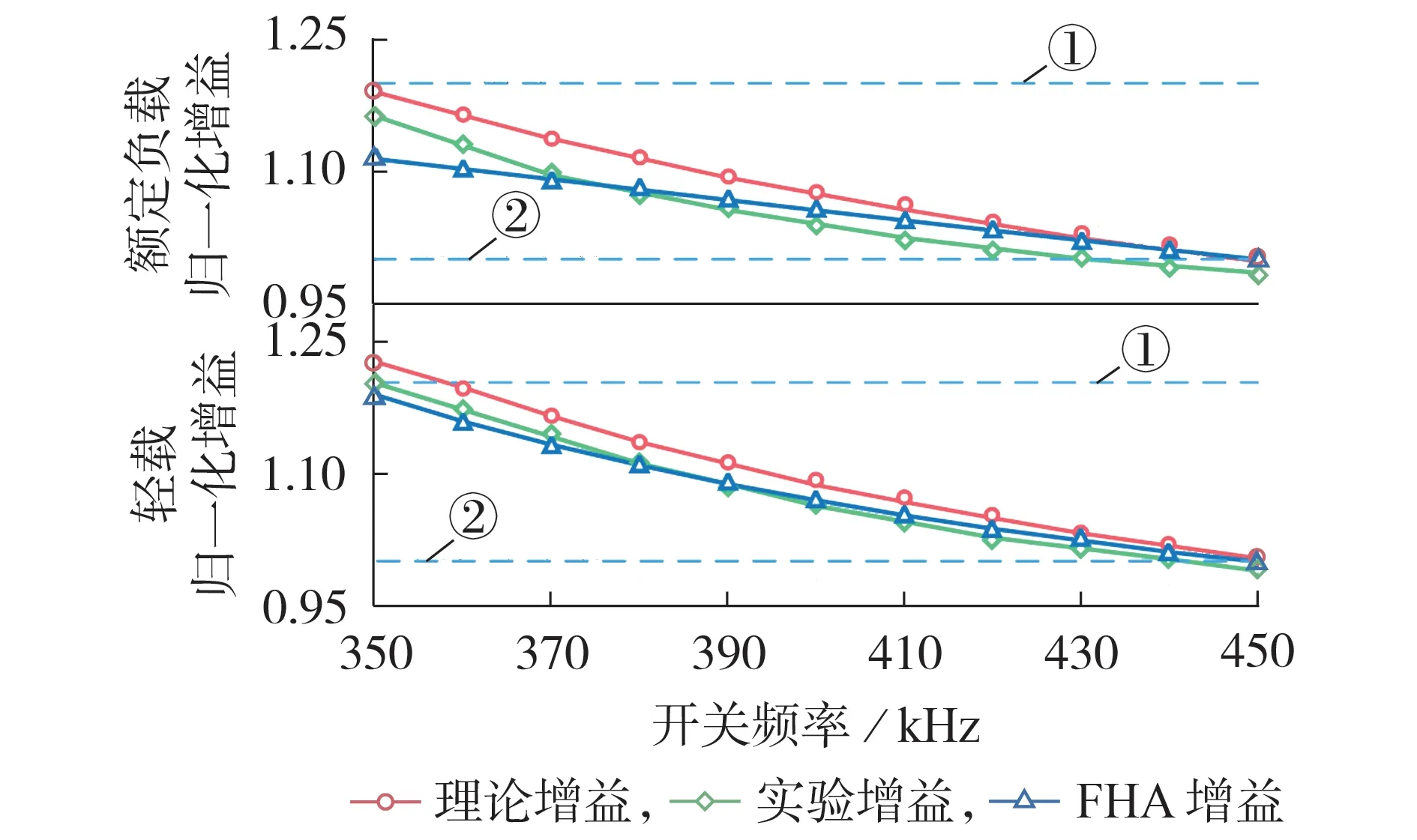
4.1 准确性验证
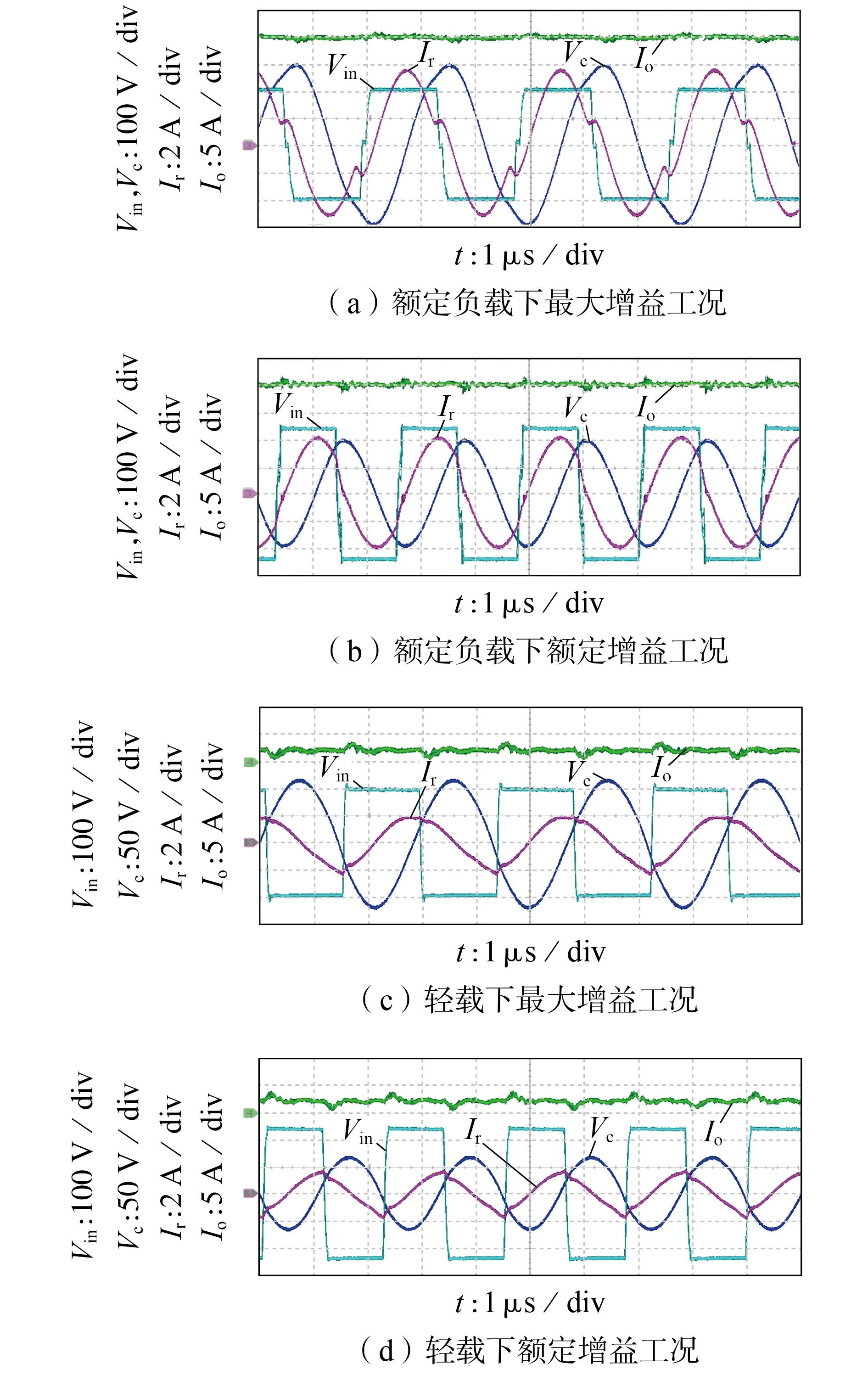
4.2 适用性验证
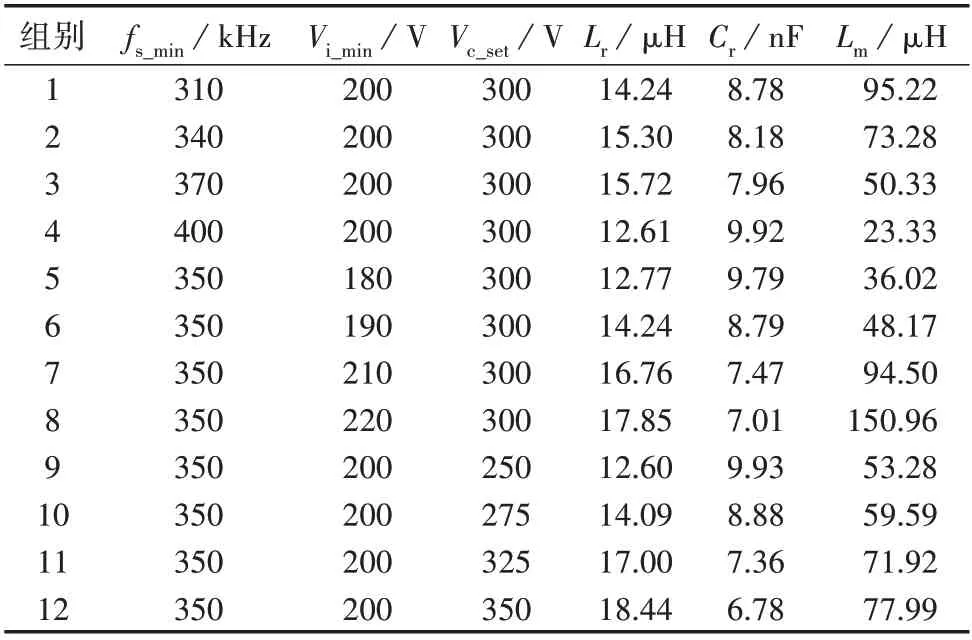
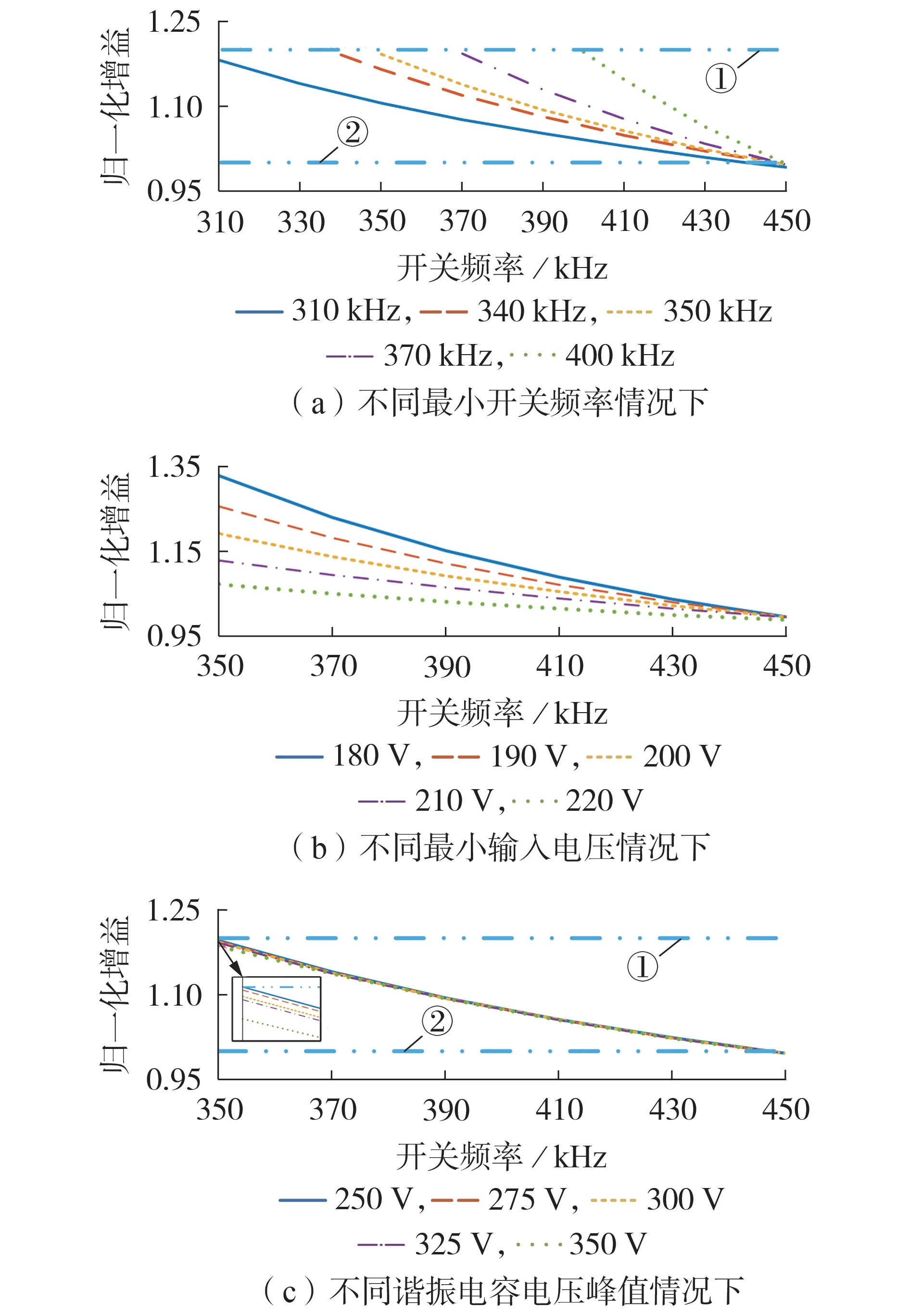
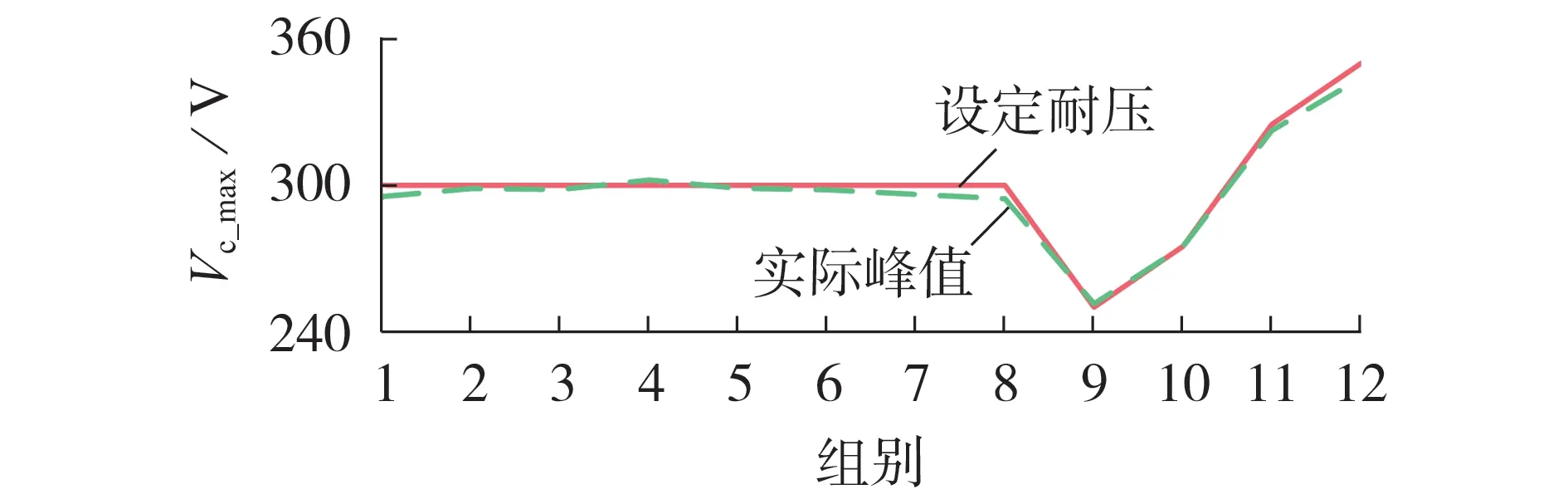
4.3 与现有方法的对比
5 结论
