LC滤波型逆变器并网电压鲁棒预测控制

郭磊磊，李伟韬，李琰琰，窦智峰，金 楠

（郑州轻工业大学 电气信息工程学院，河南 郑州 450002）

0 引言

随着风力发电、光伏发电、风光互补等新能源技术的快速发展，电压源型并网逆变器已成为电力电子领域的研究热点之一［1-3］。其中，有限控制集模型预测控制（FCS-MPC）因具有设计简单直观、无需脉宽调制、动态响应快、可实现多个非线性目标控制等优点，被广泛应用于电力电子变换器［4-6］。

在现有的研究中，文献［7］探索FCS-MPC在大功率电力电子变换器中的应用，实现了低开关频率预测控制。文献［8］分析死区对共模电压尖峰的影响，研究了一种基于FCS-MPC 的共模电压抑制方法。文献［9］将FCS-MPC 应用于感应电机，实现了无权重系数预测磁链控制。文献［10］将FCS-MPC 应用于永磁同步电机，实现了低复杂度转矩预测控制。文献［11-12］则将FCS-MPC 应用于LC 滤波型并网逆变器，实现了逆变器并网电压预测控制。然而，上述研究均未考虑参数失配的影响。由于FCS-MPC是一种基于模型的控制策略，模型参数失配对其控制性能具有较大的影响［13］。因此，近年来，诸多学者对其开展了相关研究，旨在提高FCS-MPC的参数鲁棒性。

文献［14-15］研究了带预测误差补偿的永磁同步电机FCS-MPC 方法，增强了参数鲁棒性。然而，这类方法较难实现预测误差的精确补偿。文献［16］所提方法利用当前时刻检测的负载电流和上一次计算的电流差分矢量来预测下一时刻的输出电流值，无需任何系统模型参数，参数鲁棒性较好，但动态性能较差。为了更好地补偿参数失配对FCS-MPC 的影响，文献［17］提出了一种电感在线辨识方法，实现了双向AC／DC 变换器功率的鲁棒预测控制，但该方法仅能在单位功率因数下运行。文献［18］研究了永磁同步电机的电感在线辨识方法，实现了电流鲁棒预测控制，但这需要设计复杂的电感扰动观测器。文献［19］研究了并网逆变器的电感辨识方法以实现FCS-MPC 参数的鲁棒性，但其电感辨识精度较低。为了进一步提高FCS-MPC 参数的鲁棒性，文献［20］提出了一种基于带外生变量自回归模型的预测控制方法，但该方法计算量较大。

为了避免在FCS-MPC 中使用模型参数，提高参数鲁棒性，近年来，基于超局部建模理论的无参数模型预测控制得到广泛关注。文献［21］研究了基于超局部建模理论的升压型功率因数校正（Boost PFC）变换器无参数模型预测控制。文献［22］研究了基于超局部建模理论和扩张状态观测器的永磁同步电机无参数模型预测控制。文献［23］则将无参数模型预测控制应用到了双馈风力发电机中，也取得了较好的控制效果。然而，上述文献仅研究了一阶系统的无参数模型预测控制。对于LC 滤波器型并网逆变器而言，其系统模型阶次为2，而二阶系统的无参数模型预测控制尚未得到研究。虽然文献［11-12］已开展了LC滤波器型逆变器并网电压预测控制，但其参数鲁棒性还有待提高。

基于上述研究，为了实现LC 滤波型逆变器并网电压预测控制，并增强参数鲁棒性，本文基于超局部建模理论，提出了LC滤波型并网逆变器二阶超局部模型建立方法，并推导了2 个集总扰动的计算方法。所提方法不仅可实现输出电压的无参数FCS-MPC，增强参数鲁棒性，而且省去了网侧电流传感器，节约了成本，提高了系统可靠性。设计了采用常规FCSMPC 和本文所提方法的对比实验，实验结果验证了所提方法的有效性。

1 常规LC滤波型并网逆变器FCS-MPC

1.1 LC滤波型并网逆变器的数学模型

图1 给出了典型的LC 滤波型并网逆变器拓扑结构及其逆变器并网电压预测控制框图。图中为给定的逆变器并网电压参考值；Sabc为三相桥臂开关器件的状态信号，其值为1 表示开关导通，其值为0 表示开关关断；udc为直流电压；uabc、ifabc分别为逆变器输出电压、电流；igabc为并网电流；Rg、Lg分别为并网电阻、电感；eabc为电网电压；ugabc为逆变器并网电压。LC滤波器由逆变侧滤波电感L和滤波电容C组成，R和R1分别为滤波电感和滤波电容上的寄生电阻。

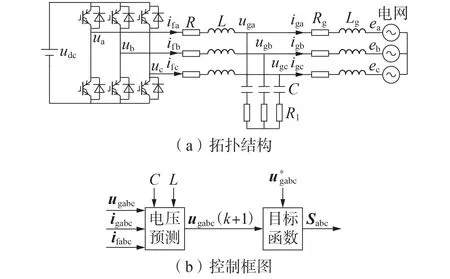
图1 LC滤波型并网逆变器拓扑结构及控制框图Fig.1 Topology structure and control block diagram of grid-connected LC filter type inverter

LC 滤波型并网逆变器在αβ坐标系中的数学模型可表示为：

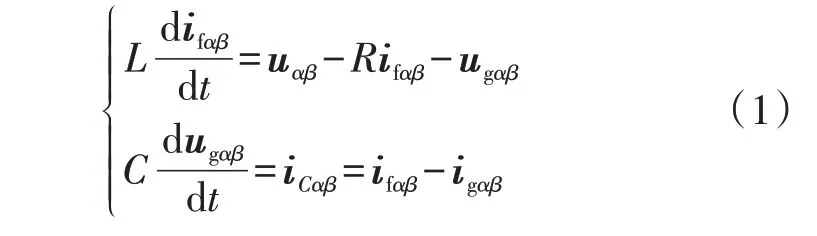
式中：ifαβ和ugαβ分别为αβ坐标系中的逆变器侧输出电流和逆变器并网电压；igαβ和iCαβ分别为αβ坐标系中的并网电流和滤波电容电流；uαβ为逆变器输出电压。由前向欧拉离散化方法可进一步推得αβ坐标系中k时刻和k+1时刻的离散方程，如式（2）所示。

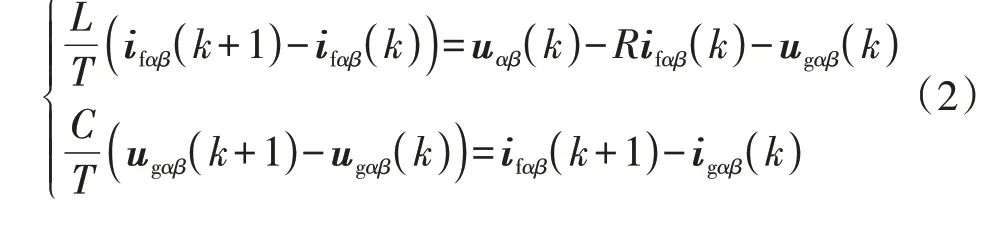
式中：T为采样周期。考虑到逆变器具有8个不同的开关状态，可以相应地生成V0—V7这8个电压矢量。在执行FCS-MPC 方法时，通常需要将这8 个电压矢量所对应的开关状态代入式（2）所示的预测模型离散方程，从而预测得到k+1 时刻的逆变器并网电压ugαβ(k+1)。最后，将预测得到的8 个逆变器并网电压代入式（3）所示的目标函数G，通过比较寻优，选择使目标函数最小的电压为最优矢量。

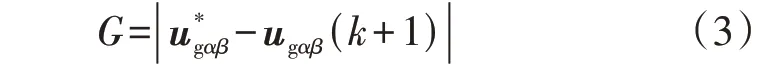
1.2 参数灵敏性分析

由式（2）可知，常规逆变器并网电压预测控制策略需要使用滤波电感L和滤波电容C及寄生电阻等参数，其控制精度严重依赖于模型参数的准确性。

为了分析参数不匹配对常规逆变器并网电压预测控制的影响，这里假设L和C分别表示实际电路的电感和电容，Lm和Cm分别表示控制器中使用的电感和电容。由于寄生电阻较小，可忽略其影响。设参数误差为Le=Lm-L和Ce=Cm-C，则式（1）可改写：

式中：变量上方“^”表示参数不匹配时该变量的估计值。由式（2）、（5）可得参数不匹配时的电压误差Δϕ为：

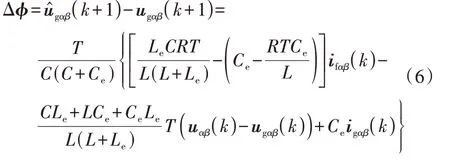
假定在当前周期电网相电压有效值eα=150 V，逆变器输出的电压开关状态对应的电压矢量为V1，输出电流有效值igα=100 A，控制采样周期T=25 μs。电压误差的绝对值| |Δϕ随Le、Ce的变化曲线见图2，图中Le、Ce为标幺值。由图可见：当Le=Ce=0 时，预测误差的绝对值| |Δϕ=0，这说明当参数匹配时无电压预测误差；并且Le、Ce同时变小对电压预测误差有很大的影响。因此，为了提高预测控制精度，需研究改进的LC滤波型并网逆变器并网电压预测控制方法。

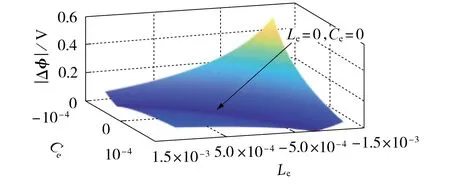
图2 | |Δϕ 随Le、Ce变化的关系曲线Fig.2 Relationship curves of| |Δϕ vs. variation of Le and Ce

2 基于超局部建模的无参数FCS-MPC

2.1 超局部建模方法与参数灵敏性分析

基于超局部建模理论的无参数FCS-MPC 可提高参数鲁棒性，已有部分学者对其进行研究［21-23］，但具有二阶模型的LC 滤波型并网逆变器的无参数FCS-MPC 尚未得到研究。本文研究LC 滤波型并网逆变器的超局部建模方法和无参数FCS-MPC方法。

对式（4）整理可得：

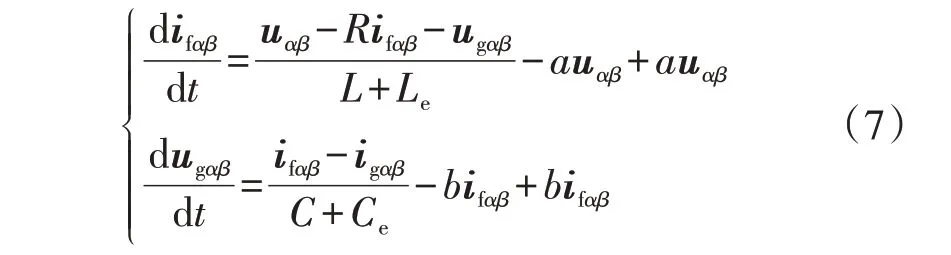
式（7）可进一步改写为：

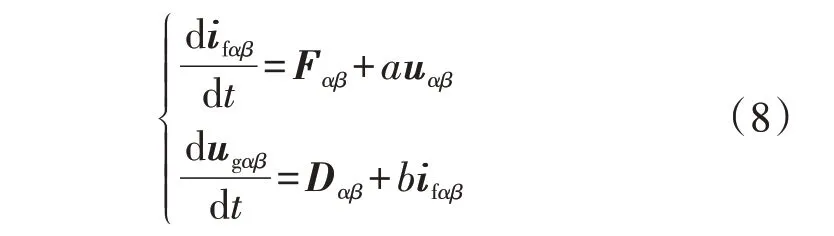
式中：a、b分别为设计超局部模型时采用的电压、电流比例系数，a通常可设为1/L，b通常可设为1/C；Fαβ和Dαβ表示式（7）中含模型参数的集总扰动。对式（8）进行离散化可得：

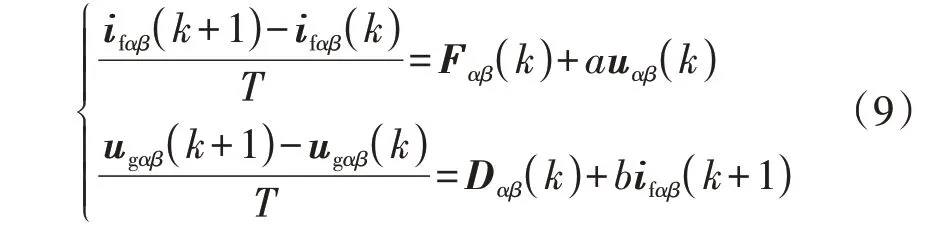
由于式（8）所示超局部模型仍需要设计2个比例系数a、b，下面对a、b变化的影响进行分析，从而为基于超局部建模方法的无参数FCS-MPC 的强鲁棒性提供理论基础。当超局部模型比例系数a、b中出现一个扰动a0、b0时，式（8）可重新表示为式（10）。

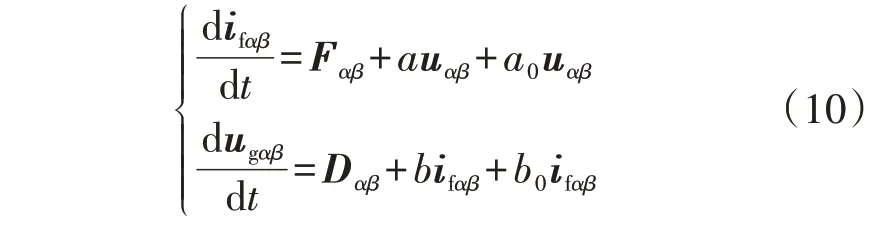
由于系统的总干扰可以由Fαβ和Dαβ来表示，包括已知的系统变量和未知的系统扰动，故可认为式中的a0uαβ和b0ifαβ为总扰动的一部分，如式（11）所示。

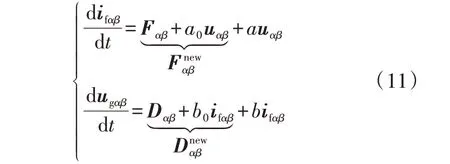
2.2 集总扰动计算方法

由式（8）可见，如何实现集总扰动Fαβ和Dαβ的计算，是实现无参数FCS-MPC 的关键。以下给出Fαβ和Dαβ的计算方法。假定在较短时间间隔内，Fαβ和Dαβ近似为常数函数。经过拉普拉斯变换可得：

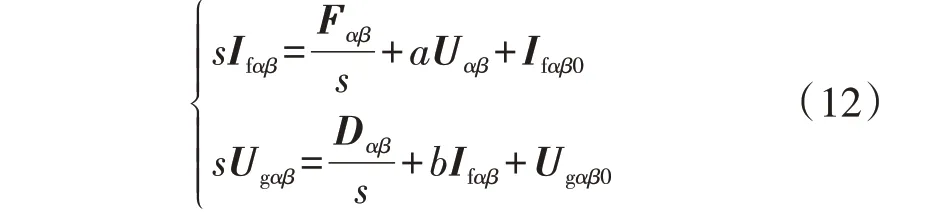
式中：Ifαβ、Ugαβ和Uαβ分别为ifαβ、ugαβ和uαβ在拉普拉斯变换中的形式；Ifαβ0、Ugαβ0分别为ifαβ、ugαβ在拉普拉斯变换中的初始值。消除式（12）初始条件，两边同时微分并乘以1/s2可得：

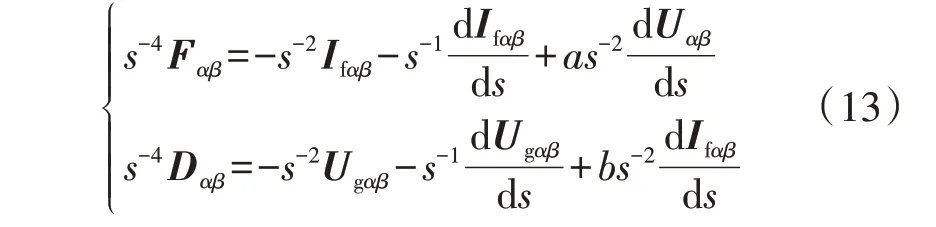
在时段［0，T］中，式（13）的拉普拉斯逆变换为：

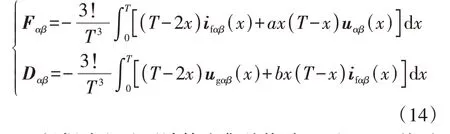
根据式（14）可计算出集总扰动Fαβ和Dαβ。然后将该计算结果代入式（9）即可实现无参数逆变器并网电压预测控制。需要指出的是，由式（14）可见，该方法无需采样电网电流，因此省去了网侧电流传感器，有助于降低系统成本，提高系统可靠性。本文经过调试后，选择10 个周期的电压、电流数据进行集总扰动计算以获得较好的动稳态性能［23］。

2.3 无参数FCS-MPC

根据上述分析，本文所提出的LC 滤波型并网逆变器无参数FCS-MPC框图如图3所示。

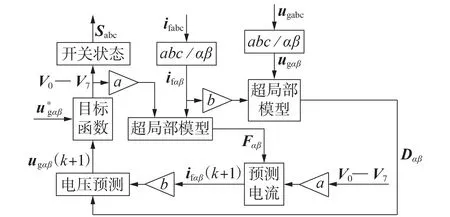
图3 LC滤波型并网逆变器无参数FCS-MPC框图Fig.3 Parameter-free FCS-MPC block diagram of LC filter type grid-connected inverter

3 实验验证

为了验证所提LC 滤波型并网逆变器无参数逆变器并网电压预测控制方法的有效性，搭建了附录A 图A1 所示的实验平台，并进行了详细的实验研究。该平台包括Typhoon602+仿真器和PE-Expert4控制器。其中控制在PE-Expert4 处理器板上执行，该处理器板由数字信号处理器（DSP）和现场可编程逻辑门阵列（FPGA）芯片组成。为验证所提控制方法的有效性以及参数预测控制的鲁棒性，本文通过实验对比研究了常规FCS-MPC 方法和本文所提控制方法的动稳态性能。实验中设置2 种控制方法的参数一致，如附录A 表A1所示。设无参数FCS-MPC方法中的系数a、b分别为416、5000。

当参考电压由220 V 突增为250 V 时，图4、5 分别给出了参数匹配条件下采用2 种方法的动态实验结果，附录A 图A2、A3 分别给出了参数不匹配条件下采用2种方法的动态实验结果。图中：λ为电流谐波幅值占基波的百分比；AF为基波电流幅值；λTHD为总谐波畸变率。

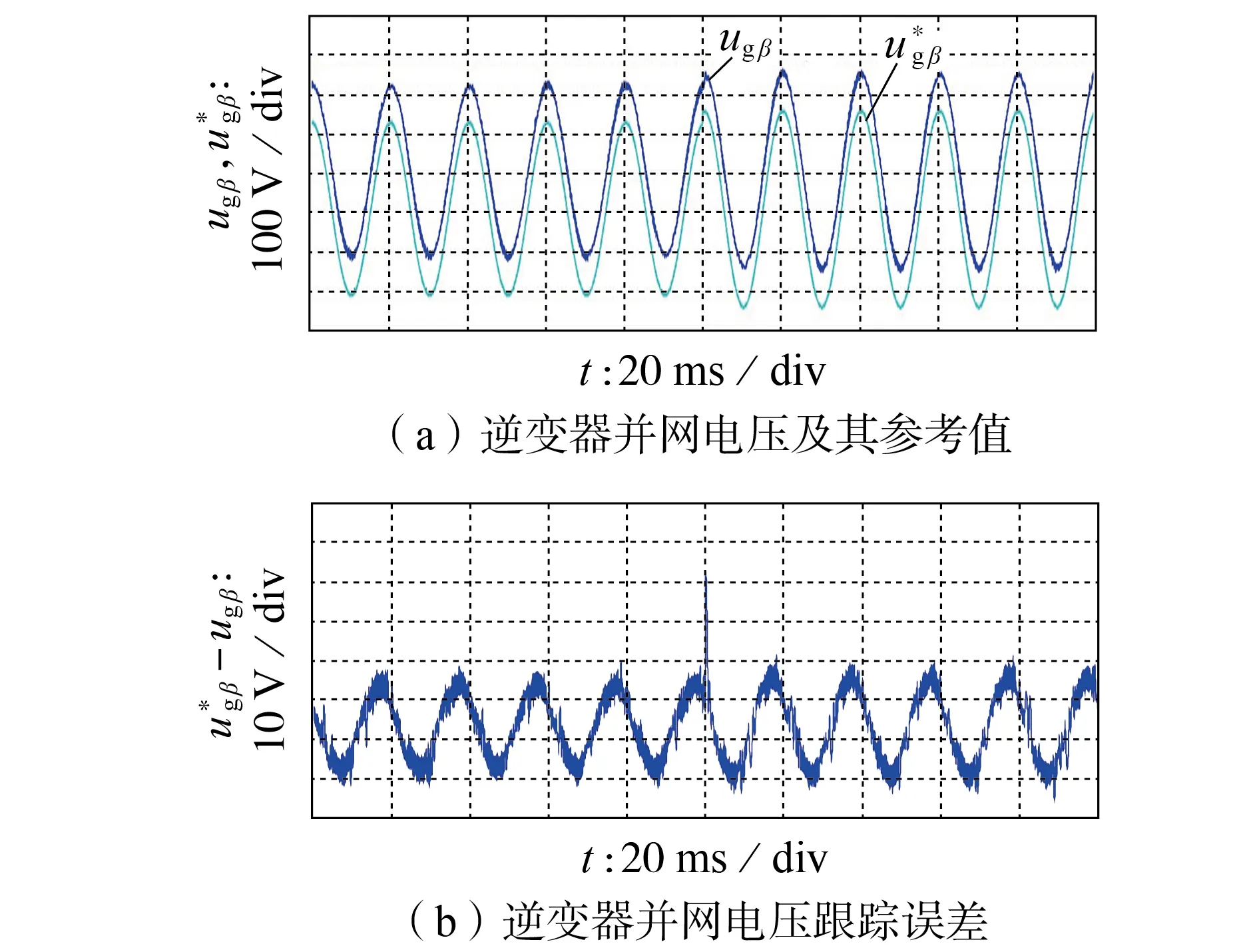
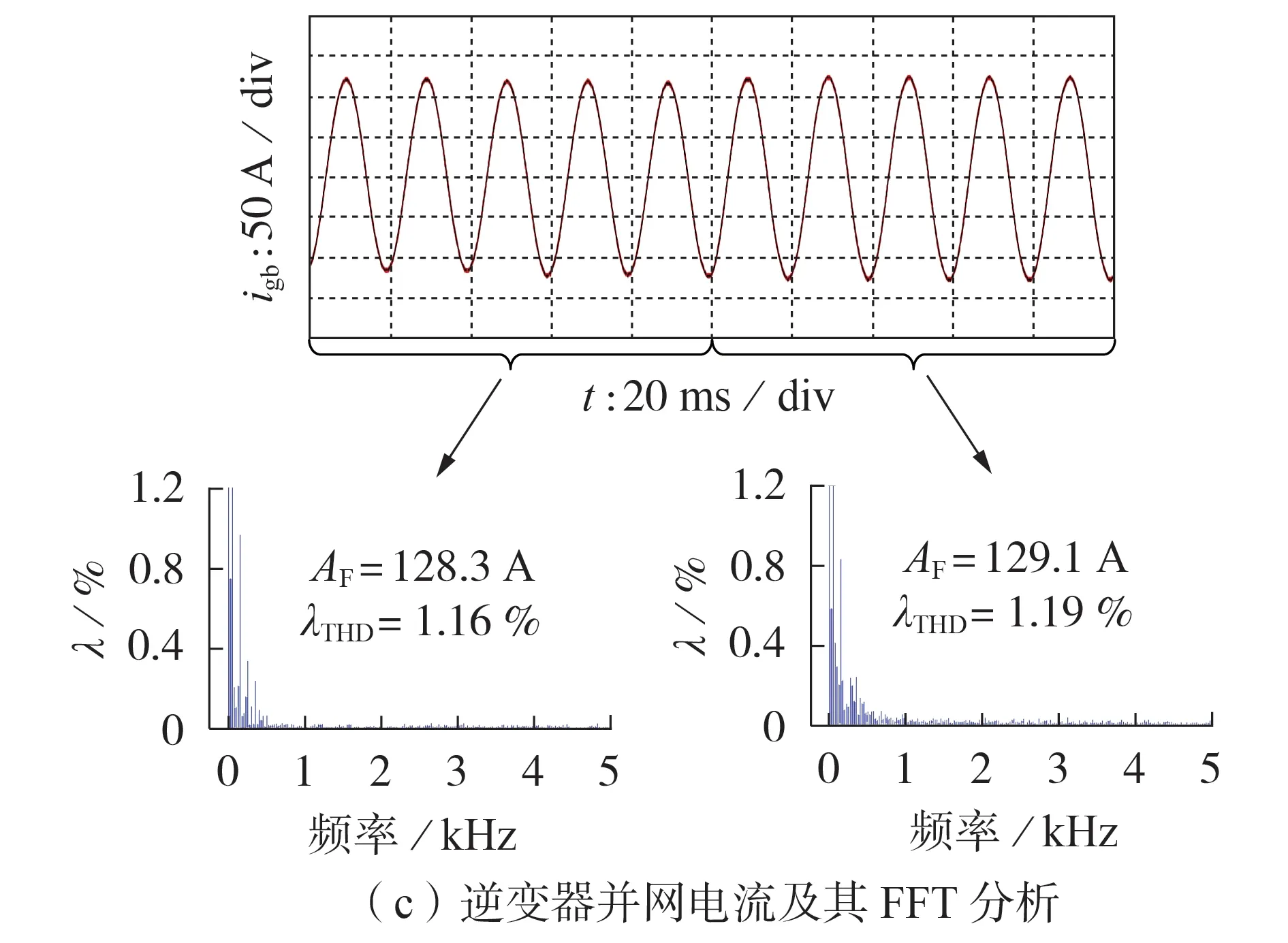
图4 参数匹配时常规FCS-MPC方法的动态实验结果Fig.4 Dynamic experimental results of traditional FCS-MPC method when parameters match

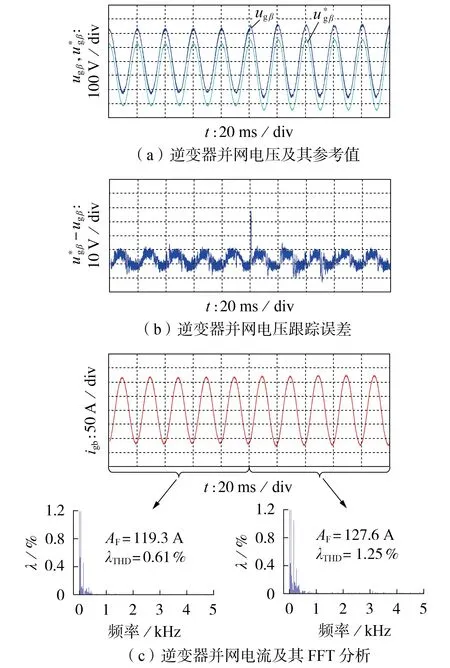
图5 参数匹配时无参数FCS-MPC方法的动态实验结果Fig.5 Dynamic experiment results of parameter-free FCS-MPC method when parameters match

根据图4、5 和附录A 图A2、A3 可知：与常规FCS-MPC方法相比，本文提出的无参数FCS-MPC 方法由于采用集总扰动的方式实时更新系统状态来预测逆变器并网电压，所产生的稳态误差较小，控制精度更高，这与理论分析一致。此外，在并网电压参考值由220 V 突变为250 V 时，2 种方法均可迅速响应给定值变化。但是，对比4 种方案（包含2 种方法下参数失配L=0.001 2 H、C=0.000 1 F 和a=632、b=7 500的情况）动态过程，如表1 所示，本文提出的无参数FCS-MPC方法所产生的动态电压峰-峰值误差较小，表明其具有更好的动态性能。同时，2种方法所表现出的并网电流谐波畸变率均能满足正常波动的范围。

表1 不同方法的动稳态性能Table 1 Performance of dynamic and steady state for different methods

此外，为了进一步验证所提方法可以有效降低稳态误差以及参数的敏感性，设定逆变器并网电压参考值为220 V，附录A图A4、A5分别给出了电感参数偏小为1.2 mH 和电感参数偏大为3.6 mH 的稳态实验结果，附录A 图A6、A7 分别给出了电容参数偏小为0.1 mF和电容参数偏大为0.3 mF的稳态实验结果。由图A4—A7可见，在电感或电容参数失配时，本文所提方法的逆变器并网电压控制误差更小，这进一步验证了本文的理论分析，证明了本文所提方法具有较强的参数鲁棒性。

为进一步验证所提方法对所设比例系数的鲁棒性，设并网电压参考值为220 V，附录A 图A8、A9 和附录A图A10、A11分别对比了a（由624变化至416、由416 变化至208）和b（由7 500 变化至5 000、由5 000 变化至2 500）变化时的实验结果。在图A8、A9中，当a由大变小时，逆变器并网电压纹波变大，稳态误差基本不变，系统仍然稳定且处于受控状态。并且当a减小到208时，逆变器并网电压控制效果基本与所设正常比例系数a=416 保持一致，表明所提方法对a的变化具有较强的鲁棒性。在图A10、A11中，当b变化时，系统仍然稳定且处于受控状态，并且当b较小时，逆变器并网电压误差较小。这表明在系统设计时可适当选择较小的比例系数b来提高所提无参数预测控制的鲁棒性和控制精度。

4 结论

本文基于超局部模型的无参数预测思想，提出了一种LC 滤波型并网逆变器无参数模型FCS-MPC方法，旨在消除常规FCS-MPC 方法对模型参数的依赖。本文详细分析了参数变化对常规FCS-MPC 方法的影响，并基于超局部建模思想设计了LC滤波型并网逆变器的二阶无参数FCS-MPC 方法，从而实现了无参数逆变器并网电压预测控制。对比实验结果表明，所提无参数FCS-MPC 方法能够有效增强参数失配时的逆变器并网电压跟踪性能，并且在稳态和动态过程中均具有较好的控制效果。

附录见本刊网络版（http：//www.epae.cn）。