计及气网管存效应的综合能源系统分布鲁棒优化调度
2022-06-15易文飞卜强生秦英明李培帅
易文飞,卜强生,路 珊,秦英明,李培帅
(1. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103;2. 东南大学 电气工程学院,江苏 南京 210096;3. 南京理工大学 自动化学院,江苏 南京 210094)
0 引言
综合能源系统IES(Integrated Energy System)可以有效接入风、光等环境友好型新能源,打破传统电、气、热、冷等异质能源之间的壁垒,提高能源利用效率[1]。发展IES是改变我国以煤为主的能源结构、推动实现碳中和目标、促进经济可持续发展的重要手段[2]。可再生能源高比例接入以及多种异质能源高度耦合等因素导致IES 呈现强不确定性、调控资源众多、高复杂度等特点,给系统的运行控制带来了极大的挑战。因此,为充分发挥和利用可控资源的潜力,研究IES 优化调度方法,从而平抑不确定性的影响,促进可再生能源消纳,具有实际研究意义。
IES中耦合有多种异质能源,相比于传统的能源系统,其优化调度问题更加复杂[3]。风电出力与需求侧用户行为的不确定性导致IES 的不确定性特征显著,极大地影响了IES 对风电的消纳。当前已有针对不确定性平抑开展的研究,如利用气网的管存等灵活性资源,提出不确定性优化方法等。IES中电网侧能量往往以光速传输,与之相比天然气传输则存在着明显的“慢特性”,气体可以暂存于管道中,即为管存[4]。文献[5]构建了气网管存模型,并且分析了该灵活性资源对于平抑不确定性的重要作用。文献[6-7]分别在IES需求响应和优化调度问题中考虑了管存这种灵活性资源的积极作用,并且取得了良好的效果。文献[8]利用Weymouth稳态潮流模型来刻画天然气气流和两端气压的关系,通过气流量差来求取管存。文献[9]采用偏微分方程来描述天然气传输的慢动态过程,虽然其可以有效刻画气体的传输过程,但是基于偏微分方程的调度优化模型往往复杂难解。作为另外一种重要的灵活性资源,IES中电力系统侧的储能系统ESS(Energy Storage Sys‐tem)可以通过充放电来实现能源的时空转移,从而起到平抑不确定性、提升系统灵活性的作用[10]。文献[11]构建了包含储能的IES 优化调度模型。文献[12]分析了储能在提高IES 运行经济性和灵活性方面的效果。但是,电力系统侧最常见的储能设备为电化学储能,充放电的深度、功率均会对其寿命产生影响[13]。当前IES 优化调度研究中,储能模型构建往往人为设置电量上下限,而鲜有分析储能充放电对其寿命影响的,通过对储能充放电进行合理调度,可以有效提高储能使用寿命,降低IES的维护成本。
上述研究通过IES 中灵活性资源的调控,降低不确定性因素的影响,但是均基于传统确定性优化方法展开,具有一定的局限性。鉴于此,有的学者提出了针对IES 的不确定性优化方法,如随机规划SP(Stochastic Programming)[14]和鲁棒优化RO(Robust Optimization)[15]方法。SP 基于不确定变量的概率密度函数假设,其鲁棒性较差;而RO 虽然具有良好的鲁棒性,但是其决策为最恶劣场景下的最优解,具有保守性。分布鲁棒优化DRO(Distributionally Robust Optimization)[16]不需要假设不确定性变量的具体概率分布,相比于SP 具有更高的鲁棒性;DRO 可以充分利用大量历史数据的概率信息,有效解决了RO保守度较高的问题。文献[17]构建了一定置信度下IES 的DRO 模型,并且对比分析了DRO 与SP、RO 的优化效果。文献[18]提出基于Wasserstein距离的IES多能流DRO方法。需要注意的是,当前DRO的相关研究中,负荷的不确定性往往和可再生能源出力的不确定性采用同样的表征方法,而且在实际运行中该2类不确定性特征是具有明显差异的。
综上,本文建立了计及气网管存效应的IES 优化调度模型,其目标函数包括风电消纳成本、常规机组CU(Conventional Unit)启停与运行成本、购气成本以及储能衰退成本。考虑不确定性因素对具有高复杂度的IES 运行的影响,构建了针对风电出力不确定性的概率分布集合以及刻画负荷不确定性的梯形模糊函数,并在此基础上建立了IES 的DRO 调度模型。最后,通过算例分析验证了本文所提方法在利用灵活性资源进行不确定性平抑、降低系统运行成本、促进风电消纳等方面的积极作用。
1 IES结构及气网管存模型
1.1 IES结构
电-热-气混联IES 实现了电力系统侧、天然气系统侧以及热网侧能源子系统间的有效耦合,其包含CU、风电机组WT(Wind Turbine)、电网侧ESS、电锅炉EB(Electrical Boiler)、热电联产CHP(Combined Heat and Power)机组、电转气P2G(Power to Gas)等设备,IES的结构示意图见附录A图A1。
与电力系统相比,IES中的不确定性因素更加复杂,对系统运行影响更加显著。一方面,IES 中各能源子系统的运行决策以及运行工况扰动均会对其他子系统造成影响;同时,由于电、气、热等能源子系统的动态特性不同,不同子系统中的设备控制特性、网络特性等具有明显的差异,相较于传统的电力系统,IES 的优化调度问题更为复杂。另一方面,风电、负荷等不确定性因素除了会对电网侧的运行工况造成影响,还会通过多种能源形式的转化而对气、热等网络系统的运行造成影响,合理地处理不确定性问题是制定多个能源网络合理的调度决策、充分发挥多种能源互补带来的高效能源利用优势的基础和前提,这对于提高IES 运行的经济性和安全性、促进可再生能源消纳具有重要意义。
气网管存是IES 中的灵活性资源,合理地对其进行利用可以平抑不确定性,提升系统运行的灵活性。针对SP 和RO 在处理不确定性方面的不足,引入DRO 理论与方法,并分别利用概率分布集合与梯形模糊函数进行了风电出力与负荷的不确定性表征。在此基础上,提出计及气网管存效应的IES DRO 调度方法,以充分发挥气网管存对不确定性的平抑作用,并通过不确定因素的分类刻画对DRO 模型进行了改进,以提高不确定环境下系统运行的鲁棒性、安全性和经济性。
1.2 天然气网络管存模型
天然气在管道中传输时具有较为明显的慢动态特性,管道可以对天然气进行存储,表现出管存效应。天然气网络的管存是一种有效的灵活性资源,其可以有效缓解IES 中不确定性的消极影响。天然气在管道中的流动状况如附录A 图A2所示,天然气管存模型[7]具体如下:
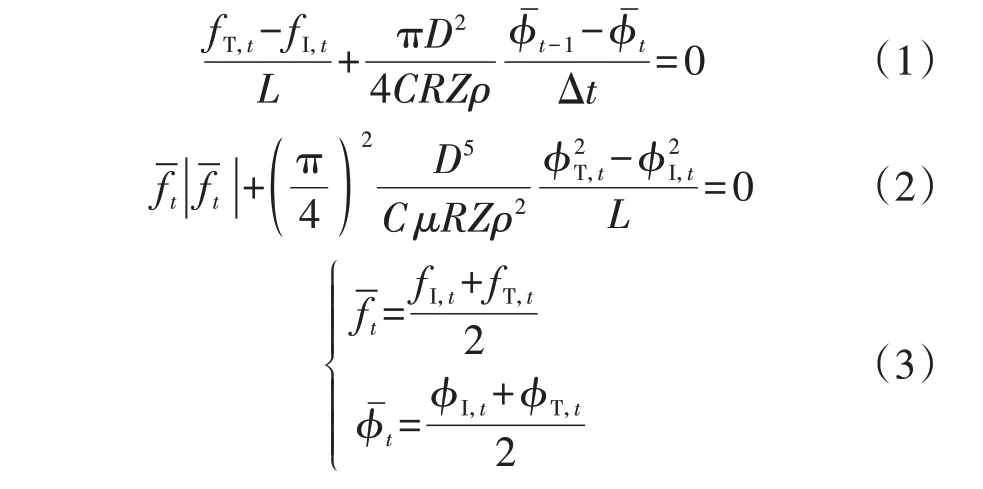
式中:下标t为调度时段的编号;Δt为一个调度时段,本文取1 h;fI,t和fT,t分别为管道起点和终点的气流量;ϕI,t和ϕT,t分别管道起点和终点的气压为管道中气流量平均值为管道中点处的气压值;L为管道长度;D为管道直径;C为气体温度;R为摩尔气体常量;Z为气体压缩系数;ρ为标准气体密度;μ为摩擦因子。
分析式(2)可知,管道中流入和流出的气流量并不相同,该气流量的差值部分留存在了管道内部,即为天然气网络管存,可以通过如下公式计算求取:
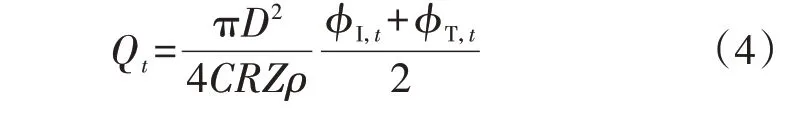
式中:Qt为管道内存储的气体体积。分析式(4)可知,管道内管存的容量与两端节点的气压相关。当末端节点的负荷增大时,节点气压降低,此时管存能力降低,气体需要向外释放,该部分释放的管存恰好可以直接供应给增大的负荷。同时,考虑到气体传输具有慢动态特性,管道内存储气体体积还与前一时段管道内气体体积有关,存在如下关系:
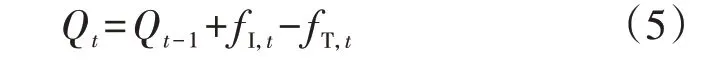
需要注意的是,式(4)与式(5)从不同角度对管存气体进行了描述,式(4)描述了同一时段下,管存气体容量与管道两端气压的关系;式(5)描述了同一管道中,管存气体容量在当前时段的值与上一时段的值的关系。
由式(2)可知,天然气管道传输流量与节点气压呈现明显的非线性特征,本文采用文献[8]中的增量分段线性化逼近法对其进行线性化处理,从而保证模型易于求解。该线性化方法不是本文的研究重点,故不再赘述。
2 IES确定性优化调度模型
2.1 电力系统约束条件
2.1.1 网络约束
1)潮流约束。
本文针对IES 电力系统侧的潮流特性,采用直流潮流模型对其进行描述,具体如下[19]:
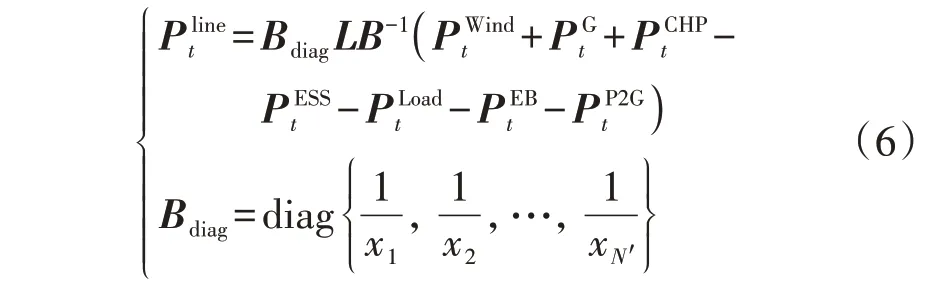
式中:xl(l=1,2,…,N′)为支路l的电抗,N′为系统总支路数;为流过支路的有功功率向量;L为系统支路节点的连接矩阵;B为系数矩阵、分别为WT、CU、CHP 机组、ESS、负荷、EB、P2G设备的有功功率向量。
2)线路传输功率约束。
系统中的线路潮流应不大于线路所能承载的最大传输功率,具体如下:
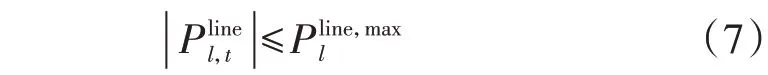
2.1.2 设备约束
1)风电出力约束。
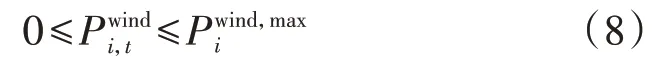
2)CU运行约束。
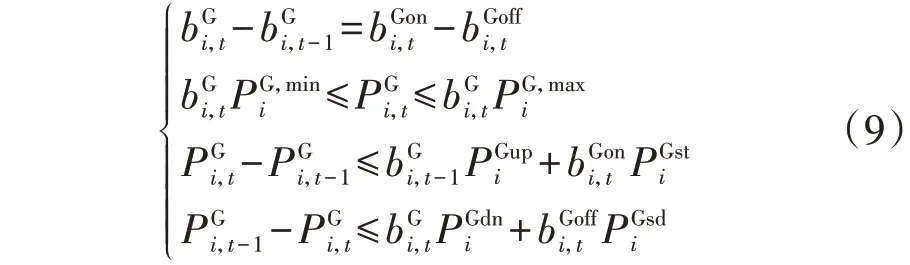
3)备用容量约束。
电力系统中通常利用CU提供运行所需正、负备用[19],其约束如下:
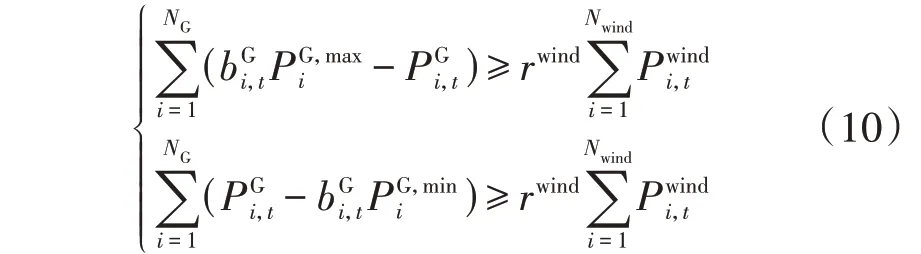
式中:rwind为风电的备用系数,取10%;Nwind为接入WT的总数;NG为CU的总数。
4)EB功率约束。

5)考虑寿命衰减的ESS约束。
ESS 的衰退成本模型描述了充放电深度对ESS寿命的影响,在IES调度中引入该模型可以对ESS的充放电深度进行有效限制,从而提高其使用寿命,具体模型见附录B[20]。在该模型的基础上,构建了ESS的运行约束,具体如下:
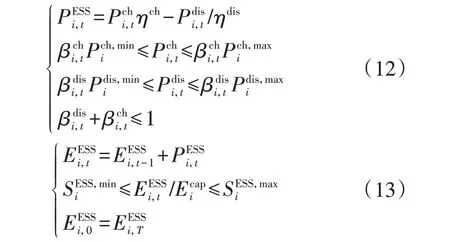
2.2 天然气系统约束条件
1)节点流量平衡约束。
对于气网中的任意节点,应满足如下节点流量平衡方程:
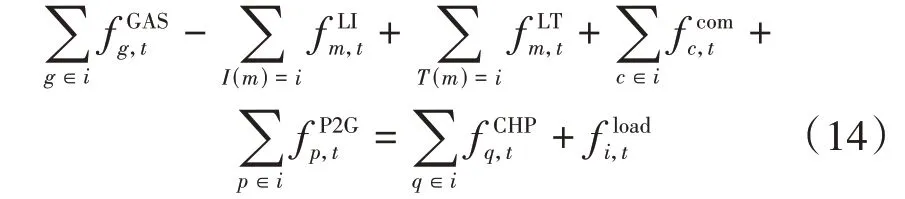
2)管道流量约束。
气网中管道内传输的气流量应在管道所能传输的最大气流量范围内,具体如下:
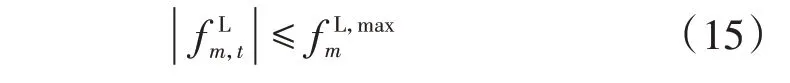
3)节点气压约束。
为了保证系统的安全运行,各节点气压不能越限,具体如下:
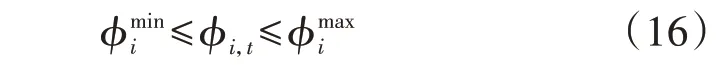
式中:ϕi,t为节点i的气压值分别为节点i的最小、最大气压值。
4)气源出力约束。
气源应在允许的范围内输出气体,具体如下:
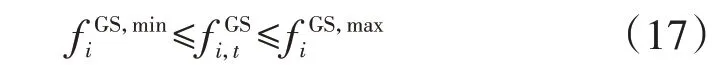
5)压缩机支路约束。
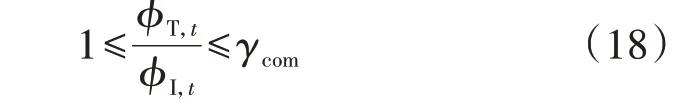
式中:γcom为气体压缩系数。
此外,天然气网络还具有流量-压力约束、管存-压力约束以及管存-流量约束,这3 类约束分别如式(2)、式(4)和式(5)所示。
2.3 热功率平衡及耦合设备约束
本文研究重点考虑了电网侧与气网侧的网络特性,热网侧仅考虑热功率平衡以及能源间的转化关系,相关约束如下。
2.3.1 热功率平衡约束
热网中的设备包括EB、CHP 设备和热负荷,在运行中应满足如下热功率平衡方程:
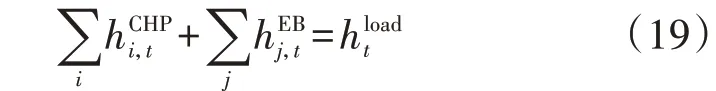
2.3.2 耦合设备约束
1)EB耦合约束。

式中:ηEB为EB的转换效率。
2)CHP设备耦合约束。
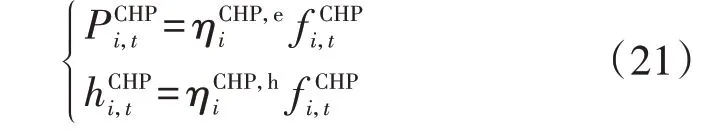
3)P2G设备耦合约束。
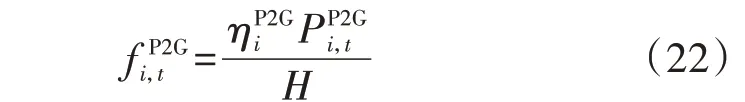
2.4 目标函数
IES 中设备众多,多种类型能源密切耦合,考虑因素与指标众多,本文综合考虑风电消纳成本CWT、CU 启停与运行成本CMT、购气成本CGAS以及储能衰退成本CBESS,建立以综合成本CCOST最低为目标的目标函数,具体如下:
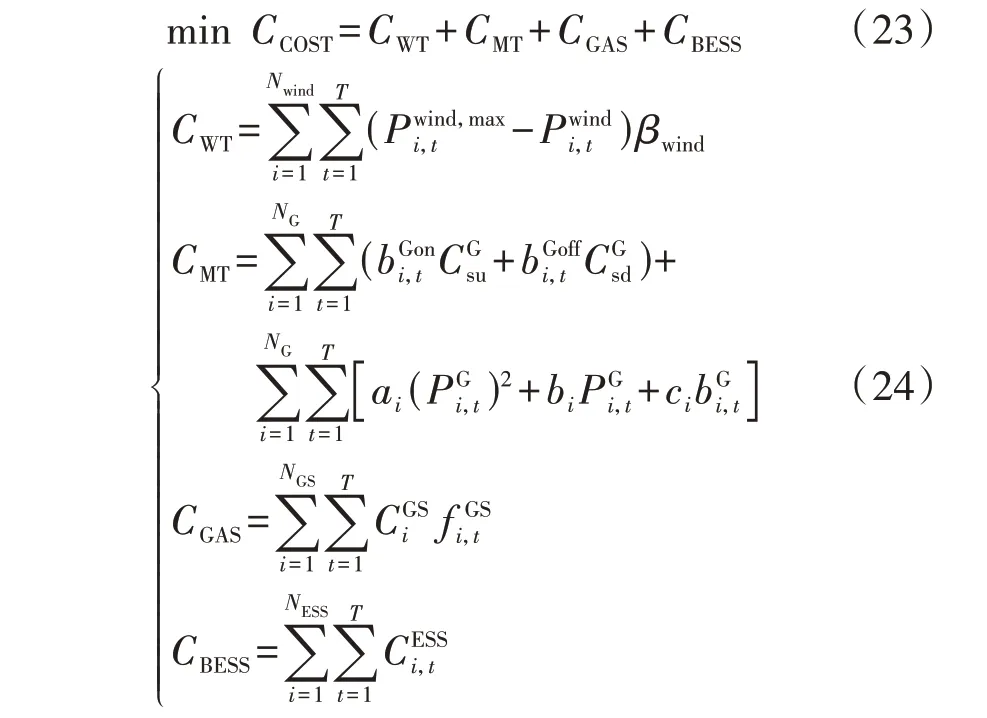
式中:T为总的调度周期为WTi的预测出力值;βwind为单位弃风成本系数和分别为CU的开机成本和关机成本;ai、bi和ci为与机组i有关的发电成本参数;NGS为天然气源的总数为天然气源i的购气单价成本;NESS为储能设备的总数;为储能设备i的衰退成本,具体表达式可以参考附录B所示的ESS的衰退成本模型。
3 DRO模型及求解算法
3.1 风电及负荷不确定性表征
风电出力具有较强的不确定性,本文基于场景信息建立风电出力概率分布集合。在M个历史运行场景中通过聚类挑选出K个参考样本,并获得各自的初始概率分布值。使用概率允许偏差值θ1、θ∞来约束概率分布集合的范围,其数值可以根据概率置信度水平计算得到。实际分布与参考分布之间存在一个误差允许范围,误差值在允许范围内的概率即为置信度水平。
设每个场景发生的概率为pk,则以初始概率为中心,综合考虑在1-范数和无穷范数约束下的概率允许偏差值θ1、θ∞,可以构建如式(25)所示的概率分布集合。
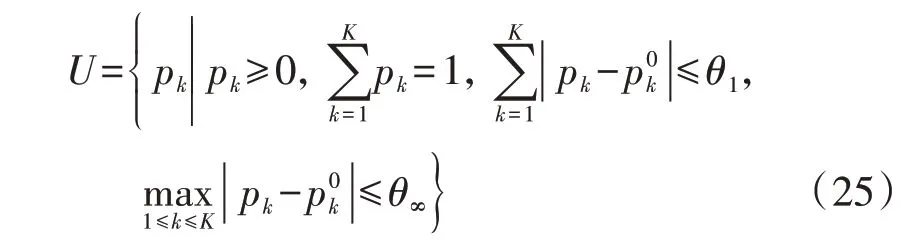
设2 个范数的不确定性概率置信度为α1和α∞,则1-范数和无穷范数允许概率偏差值θ1、θ∞可分别表示为[21]:
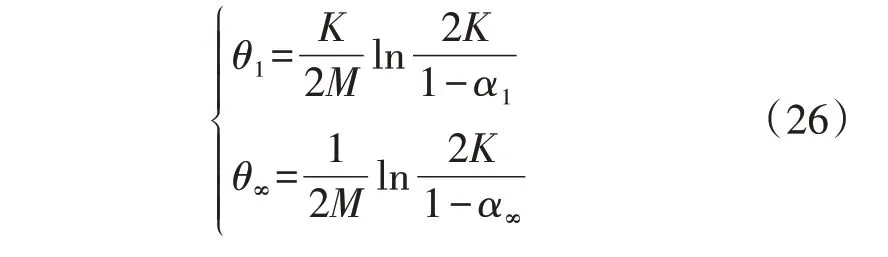
负荷水平是由居民的日常生活需求所决定的,其预测信息的准确度比较高,波动性没有风电明显,变化具有一定的规律性。计及负荷的同时性效应,负荷的不确定性变化仅会影响幅值的变化,而负荷的波动规律不变[22]。因此本文选择使用梯形模糊等价模型来表示负荷的不确定性,梯形模糊等价模型可以表示为:
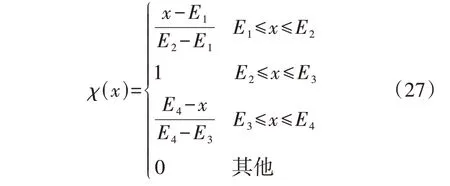
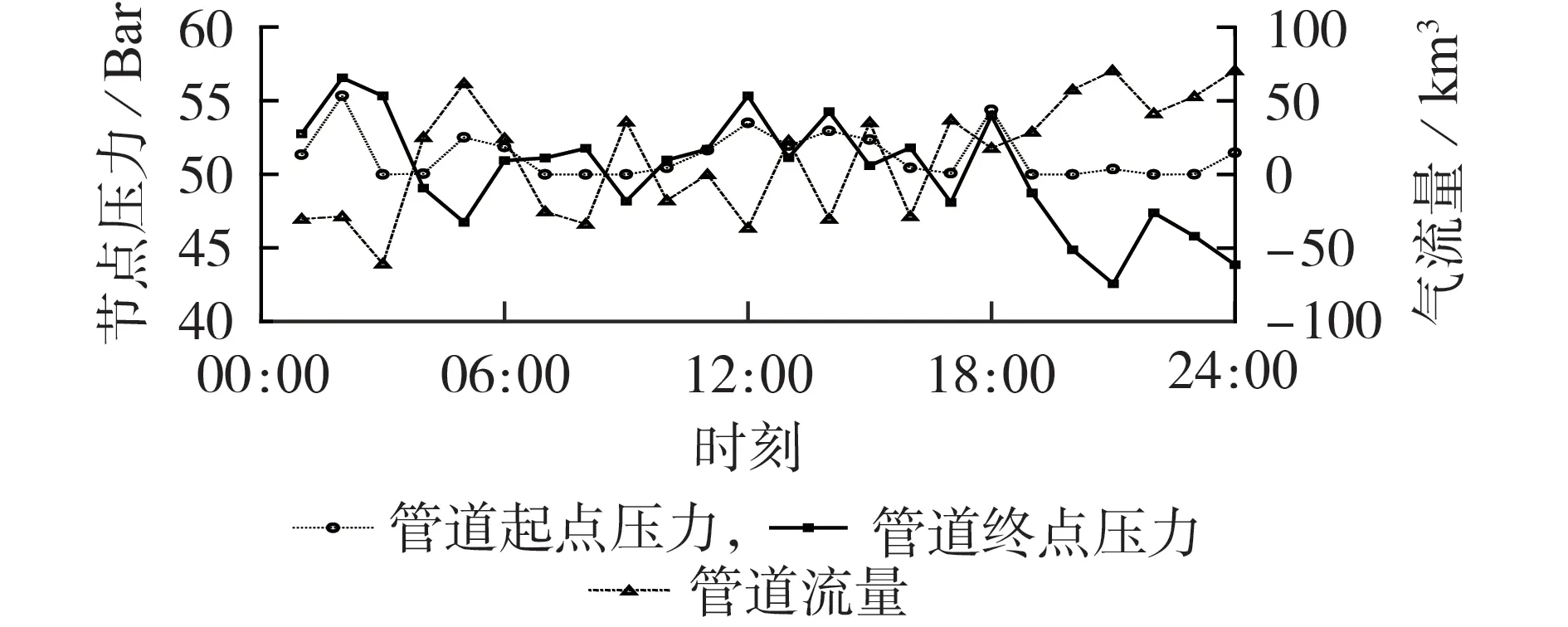
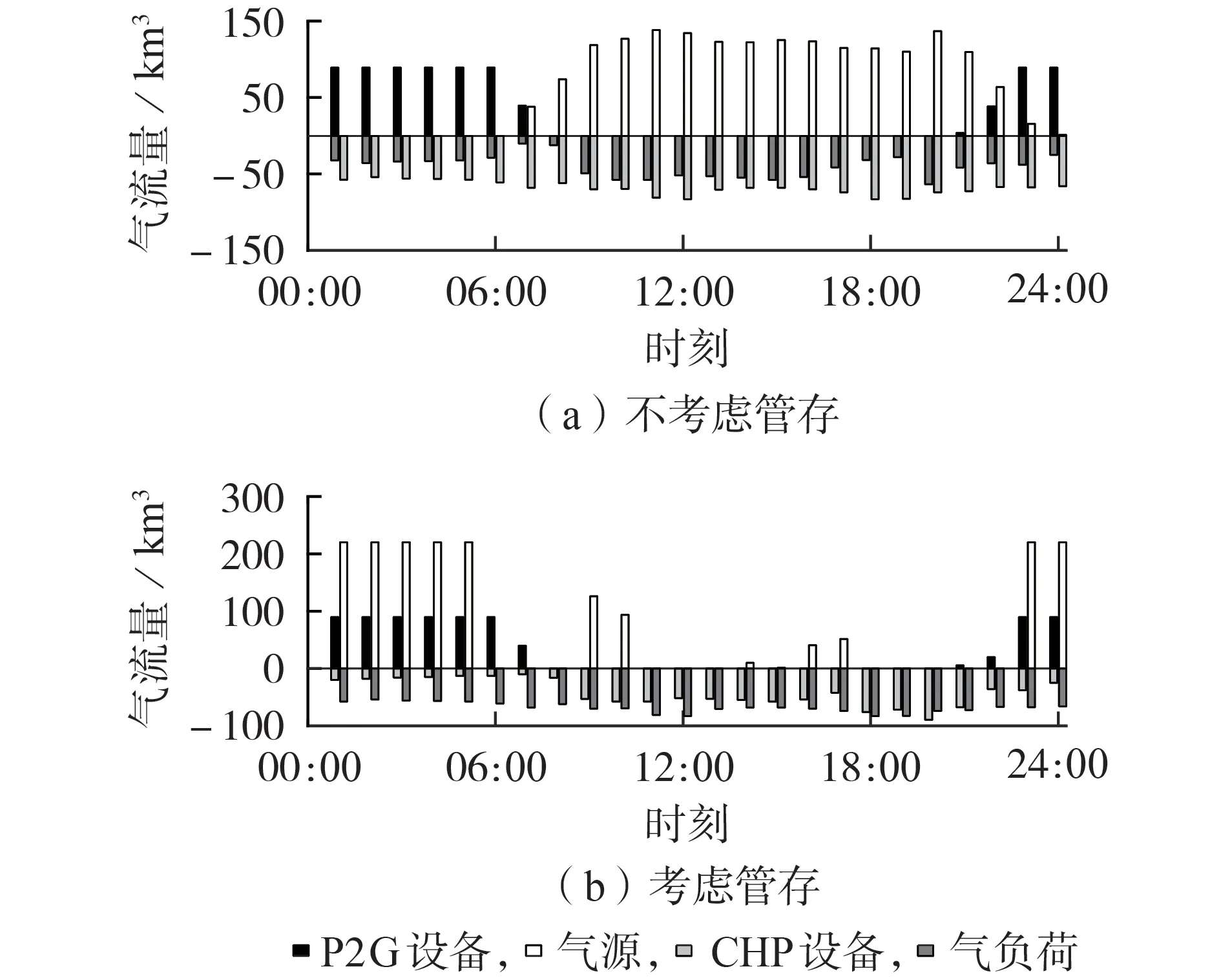
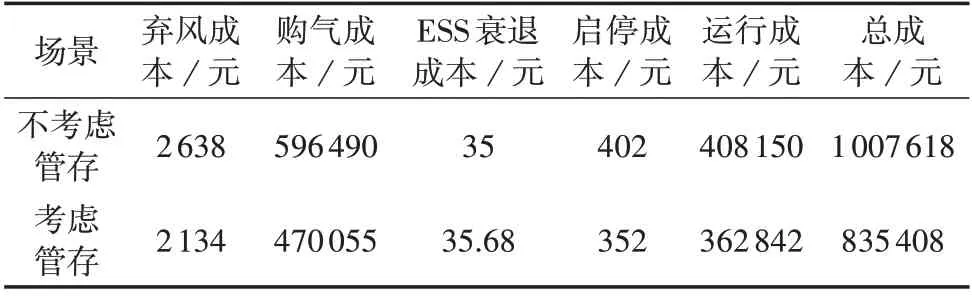
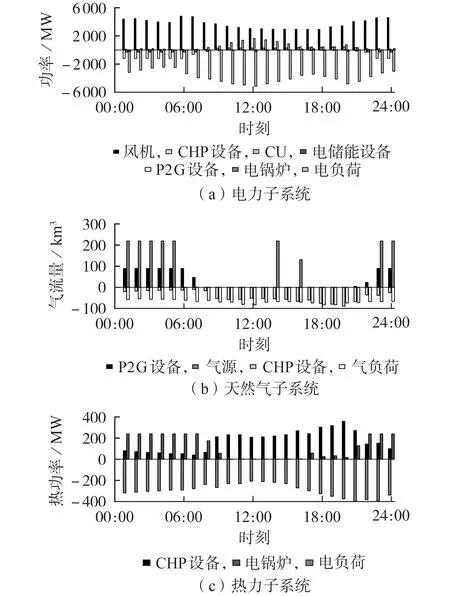
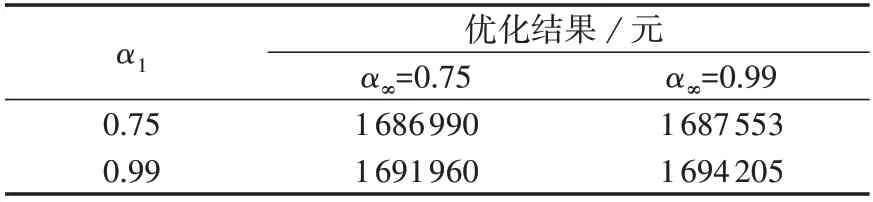
式中:χ(x)为隶属度函数;E1—E4为隶属度函数的参数,可以根据历史数据进行确定,其满足E1 该模型直接应用于计算求解比较困难,采用文献[23]中的方法可以将其转化为如下易处理的等价模型: 式中:ψ为置信度水平,且满足0≤ψ≤1。 故考虑不确定性时的负荷模型可以表示如下: 式中:P͂L为负荷模糊度函数;PL,1—PL,4为负荷隶属度函数的参数,且PL,1≤PL,2≤PL,3≤PL,4;Ki为比例系数;为负荷的预测值。 由上述分析可知,使用梯形模糊等价模型可以根据不同的置信水平,将负荷的不确定性转化为不同水平下的确定性出力,在保持一定准确度的同时降低了模型的复杂度和计算的难度。 基于上述风电出力不确定性以及负荷模糊函数不确定性表征,本文建立了IES DRO 调度模型。第一阶段变量包括CU 的启停变量、EB 和CHP 设备的启停变量以及ESS 运行的相关变量,其余变量均设置为第二阶段变量,目标函数如下: 式中:x为第一阶段变量;y0为预测场景下的第二阶段变量;u0为不确定变量的预测值;x∈X和y0∈Y(x,u0)分别为第一阶段和第二阶段变量的可行域;y为参考场景下的第二阶段变量;u为参考场景下的不确定变量;a、b、c分别为第一阶段变量、第二阶段变量和不确定变量的系数;p(u)为不确定变量u的概率分布函数;Ep[·]表示求期望值。 进一步地,基于不确定变量刻画对式(30)中最小值的期望进行转换,将期望表示为每个场景的目标函数乘以各自的概率值pk。则两阶段DRO模型的目标函数可以转化为: 式中:yk和uk分别为第k个场景下的第二阶段变量和不确定变量;yk∈Yk(x,uk)为由第一阶段变量和第k个场景下的不确定变量所确定的第二阶段变量的约束。 本文针对上述两阶段DRO 模型采用列约束生成算法C&CG(Column-and-Constraint Generation)进行求解,将原始DRO 问题分解为1 个主问题和1 个子问题,进行主问题和子问题的交替迭代求解。该算法的详细求解过程见文献[19],此处不再赘述。 为充分验证所提模型和方法的有效性,本文基于MATLAB 2018b 软件展开算例分析,所有模型和算法的编程均基于YALMIP平台,并通过调用Gurobi求解器进行求解。基于IEEE 39 节点电力系统[19]和比利时20 节点高热值天然气网系统[24]构建了仿真系统,系统拓扑见附录C 图C1。需要注意的是,本文测试系统虽然考虑了电、气、热3 种能源类型,但并未考虑热网侧网络系统,仅考虑了热负荷。 该测试系统包含CU、天然气源、储能、P2G 设备、EB 以及CHP 机组等多种设备,设备参数见附录C 表C1—C6;电负荷、气负荷和热负荷的预测值见附录C 图C2;天然气分时价格见附录C 图C3[17]。此外,气网初始管存为1.3×107m3[25],电负荷的基准值为5500 MW,气负荷的基准值为300 km3/h,热负荷的基准值为600 MW。本文以风电出力预测值为平均值、预测值的25%为方差,采用正态分布生成了500 组初始场景,通过场景聚类获取了10 个典型场景,典型场景下的风电出力见附录C图C4。 1)气网管存特性分析。 为验证气网管存特性、所建天然气管道模型的准确性,本文针对管道中天然气流动的情况进行了分析,其中管道11 的流量与两端节点压力如图1所示。 图1 管道11的气流量与两端节点压力Fig.1 Gas flow and nodal pressures of both ends of Pipeline 11 分析图1 可知,管道内部气体流动的方向由两端节点的压力值所决定。当起点的压力值高于终点时,气体流动方向为正,从起点流向终点,且流量的大小与压力差值大小有关,两端压力差值越大,流量越大。该结果与式(4)相对应,验证了模型的准确性。 为充分验证气网管存作为灵活性资源在提高系统经济性、促进风电消纳方面的作用,本文分别构建了不考虑气网管存和考虑气网管存2 个场景,并通过对这2个场景下IES优化调度模型进行求解,获取了气网平衡状态以及2 个场景下的运行成本,气网平衡状态如图2所示。 图2 气网平衡状态Fig.2 Equilibrium state of gas network 分析图2 可知,考虑气网管存特性时,气源购气均发生在气价最低的凌晨和夜晚,以及气价次低的空闲时段,可以有效降低购气成本。此外,若不考虑管存,为实现气网平衡,CHP 设备需要在01:00—06:00 时段消耗更多的天然气来发电,造成电压抬升,影响风电消纳。因此,充分利用天然气管道管存效应可以有效提高CHP 机组运行的灵活性。在16:00—17:00 时段,气源提前进行了购买操作,节省了成本,同时避免了高峰时段的管道拥挤。在23:00—24:00 时段,气源大幅购买天然气是为了使管道内的气体水平升高到调度周期最开始的水平,便于下一个调度周期的运行。由此可见,利用气网管存可以在气网中实现错峰购气,在电负荷高峰时段还可以提供额外的能量支撑,在节省购气成本的同时促进了耦合网络的优化运行。 2个场景下的IES运行成本如表1所示。 表1 不同场景下的运行成本对比Table 1 Comparison of operation cost under different scenarios 分析表1 可知,考虑气网管存时,弃风成本得到有效降低,说明弃风现象明显减少,这是由于P2G设备可以更少地消纳天然气,从而提高风电消纳效率。此外,购气成本降低了21.196%,运行成本降低了11.101%,总成本降低了17.091%。这是由于充分利用了气网管存,可以在风电出力较高时,利用P2G设备存储更多天然气,安排更为合理的CU启停计划和运行计划,进行合理的购、售气,从而全面降低运行成本。 2)DRO结果分析。 设置α∞=0.99、α1=0.99,负荷模糊集合中置信度水平为0.6,求解本文所建IES DRO 优化调度模型,获取各子系统运行工况,如图3所示。 分析图3 可知,IES 中天然气购气发生在凌晨以及14:00和16:00,此时均为气价较低时段,进一步证明了气网管存这一灵活性资源在IES 优化调度中的积极作用。对比图3(a)—(c)可知,CHP设备通过大量消耗天然气来进行产热,供给电负荷的反而较少,促进了利用风电来进行电负荷的供给,从而减少了弃风现象,说明了DRO 决策在平抑不确定性方面的有效性,其可以促进风电的消纳。 图3 基于DRO的IES各子系统运行工况Fig.3 Operation condition of sub-systems in IES based on DRO 3)负荷与风电不确定性参数影响分析。 在本文所建的DRO 模型中,建立概率分布集合时需要设置的参数有实际运行场景数M、参考场景数K、1-范数置信度α1、无穷范数置信度α∞以及负荷置信度。为了分析各参数在模型中所发挥的作用,按照运行需求对参数进行合理的设置,构建不同参数下的案例进行对比分析。 首先,设置风电概率分布集合中α∞=0.99、α1=0.99、M=500、K=10,调节负荷模糊集合中的置信度水平,各运行成本如附录C 表C1 所示。令α1和α∞分别在0.75、0.99 中进行取值,获取风电在不同置信度下的分布鲁棒模型计算结果如表2所示。 表2 不同置信度下的优化结果对比Table 2 Comparison of optimal results under different confidence coefficients 由表2 可以看出,随着1-范数置信度α1和无穷范数置信度α∞的减小,分布鲁棒模型的优化结果都在降低,其中无穷范数置信度α∞减小时对结果的影响更大。根据相关概率理论,置信度的减小会导致置信区间变窄,不确定性降低,系统调度难度减小,因此系统运行成本相应会下降,验证了所提模型计算结果的准确性。 利用同样的方式分别生成1000和1500个数据,其余部分的处理方式与上文相同,取α1=0.99、α∞=0.99,求得场景数为500、1000和1500时的优化结果分别为1 694 205 元、1 687 067 元和1 686 631 元。可见随着历史场景数的增加,DRO 模型的计算结果逐渐减小,原因是随着场景数的增加,恶劣场景出现的频率逐渐减小,正常场景出现的频率逐渐增加,因此在概率分布集合中恶劣场景出现的概率降低,导致最终计算结果减小。从概率理论方面进行分析可以发现,历史场景数的增加与置信度的减小给模型带来的影响是相同的,也从侧面验证了计算结果的准确性。 本文针对耦合电、气、热3 种能源的IES,提出计及气网管存效应的DRO 调度方法,从而促进风电消纳,降低系统运行成本,提高系统运行安全性。考虑天然气传输中的气体流动的物理特性,构建天然气网络管存模型,进而构建了IES 优化调度模型;在此基础上,针对风电与负荷不确定性特征的差异性,分别采用分布概率集合以及模糊函数构建对应的不确定集,进而构建了DRO 调度模型,并通过C&CG 算法进行了求解。 算例分析表明所提方法在不确定性环境下具有良好的适应能力,合理利用管存效应可以有效提高系统调度灵活性;合理地进行不确定性刻画,可以进一步降低优化决策的保守度,同时提高风电消纳能力。本文所提DRO 方法对不确定性优化问题,如微电网的能量管理具有较强的借鉴意义。 附录见本刊网络版(http://www.epae.cn)。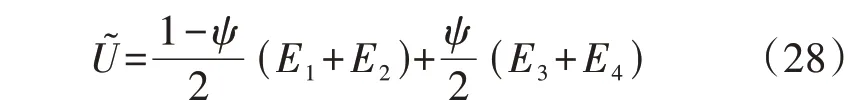
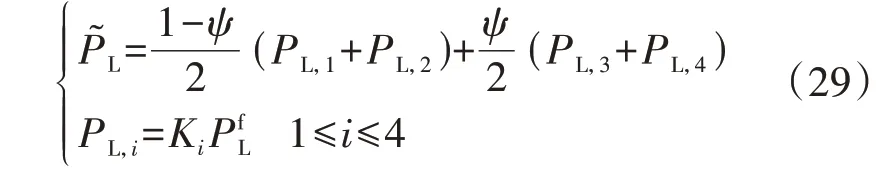
3.2 DRO模型
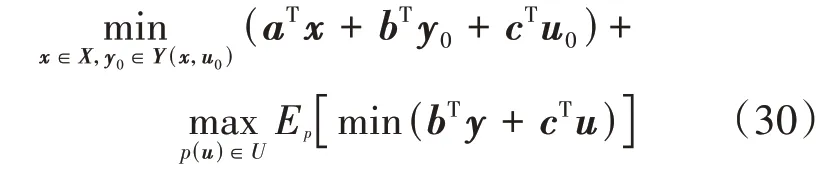
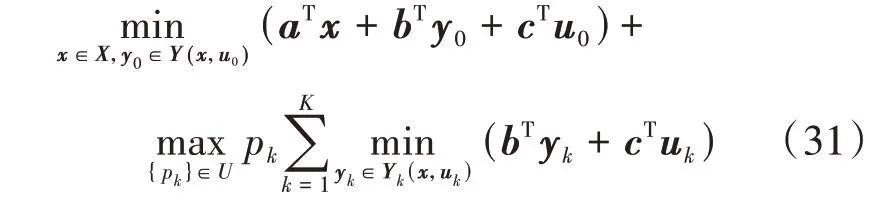
4 算例分析
4.1 算例介绍
4.2 结果分析
5 结论
