同步流区域内速度和车间距统计分析研究
2022-06-15符鼎俊李启朗
符鼎俊,李启朗
(安徽建筑大学 数理学院,安徽 合肥 230601)
交通发展给人们的出行带来了诸多便利,提升了经济运行效率。然而,随着交通的快速发展,产生了诸如交通拥堵、环境污染等问题,因此,解决交通拥堵问题成为了交通领域研究的重要课题[1-4]。道路交通中车辆的动态行为是复杂的,具有自组织、交通状态共存以及非均衡性等特征[5]。为了研究交通流演化机理,学者提出了多种模型,如跟驰模型、元胞自动机模型、流体动力学模型等[6]。元胞自动机模型是一种微观交通流模型,模型中的时间和空间是离散的,交通流的演化用更新规则描述。元胞自动机模型演化规则灵活、计算效率高,适用于模拟真实道路交通流的演化情况[7],且元胞自动机模型也为三相交通流的发展做出了巨大贡献。三相交通流理论将拥挤流进一步分为同步流和宽运动堵塞,因此,交通流有三个相,即自由流(F)、同步流(S)以及宽运动堵塞(J)[7-9]。根据道路交通经验数据集,交通流量从大到小对应着自由流到同步流的转变(F→S)、同步流到宽运动堵塞的转变(S→J),而自由流直接过渡到宽运动堵塞(F→J)很少发生[9]。在同步流中,其车辆平均速度比自由流低,但比宽运动堵塞的车辆平均速度高,平均流量有时和自由流一样高。本文基于三相交通流理论以及文献[10]中的演化更新规则,研究在同步流区域的均匀分布、致密分布以及随机分布下不同密度对车辆速度分布和车间距分布的影响。
1 模型及其演化规则
模型的道路条件为单车道,用L表示单车道的长度,其中,L由一维离散的元胞组成,每辆车占据一个元胞(cell)。车辆的速度v=0,1,2,…,vmax,其中,vmax为正整数,最大速度设置为5,不允许超车,采用周期性边界条件。相邻车辆之间的间距用Gap表示,指的是本车车头(车头保险杠位置)与前车车尾之间的空元胞数。道路在t+1时刻的状态可从t时刻通过对所有车辆应用以下4个步骤(并行动力学)得到。
Step1如果vi=0且Gap=1,则以概率p=0.25进行加速,加速更新规则为vi(t+1)→min(vi(t)+1,vmax);其余情况,则以概率p=1进行加速,加速更新规则如上所述。
Step2由于其他车辆的减速,减速更新规则为vi(t+1)→min(vi(t+1)+1,Gap)。
Step3当速度大于等于2,小于等于4时,以概率p(vi(t+1))=0.5进行随机慢化,随机慢化更新规则为vi(t+1)→max(vi(t+1)-1,0)。
Step4车辆移动更新规则为xi(t+1)→xi(t)+vi(t+1),其中vi(t)和xi(t)分别为当前时间步长t下第i辆车的速度和位置。
本研究在初始分布下的随机慢化概率取p=0.5,因为慢化概率越大,致密分布和随机分布的同步流占据的密度范围越宽广,有助于探讨其同步流的内部机理。
2 数值模拟分析
计算机模拟的单车道L由2 000个元胞组成,每个元胞长度为7.5 m,相当于实际道路长度15 km,一个时步长近似相当于实时的1 s,最大速度vmax=5在实际交通中对应135 km/h。道路上总车辆数为N,车辆密度为D=N/L。每次测试进行50万时步以消除瞬态影响,连续记录最后1万时步的数据。为了消除初始分布的随机性对结果的影响,再对50个样本取平均。
均匀分布指车辆均匀地分布于道路中,每两辆车的车间距相同;致密分布指每辆车紧跟着前车,相邻车辆之间的车间距为零。车流量、速度、密度分别用Flow、Velocity、Density表示,对应的单位分别为veh·s-1、m·s-1、veh·m-1。时步、位置分别用Timestep、Position表示,对应的单位分别为s和7.5m。车间距最小值为0,最大值为1 999,本次研究统计了车间距为0至20的分布情况。
2.1 均匀分布
均匀分布的基本图(包括自由流、同步流以及宽运动堵塞)如下页图1(a)所示,其中绿线标注的是自由流、蓝线标注的是同步流、红线标注的是宽运动堵塞,这是典型的三相交通流基本图。在三相交通流中,同步流是非常重要的一种交通状态,其速度特征比较复杂,如下页图1(b)~(d)所示。每个速度值在不同密度下所占据的百分比值虽有差异,但又呈现一定的规律。当密度相对较低时,v=1、v=2、v=3、v=4所占据的百分比值随着密度的增加而增加,其中,v=1、v=2、v=3的百分比值增加的较为明显,如图1(b)所示;当位于同步流的中间密度时(D=0.2附近),v=1和v=2所占据百分比值依旧随着密度的增加而明显增加,但v=3和v=4所占据的百分比值却近似相等,如图1(c)所示;当密度相对较高时,v=1所占据的百分比值随着密度的增加而增加,v=2、v=3、v=4所占据的百分比值却随着密度的增加而减少,如图1(d)所示。值得注意的是,v=5所占据的百分比值始终随着密度的增加而减少。
图1(b)~(d)没有显示速度为0的分布情况,其原因是同步流区域中没有车辆停下来。由于本文的基本图模型是双巡航控制极限模型,随机慢化规则中v=1和v=5不慢化,因此图1(b)、(c)、(d)中速度为2、3、4的百分比值都比速度为5和1的低。
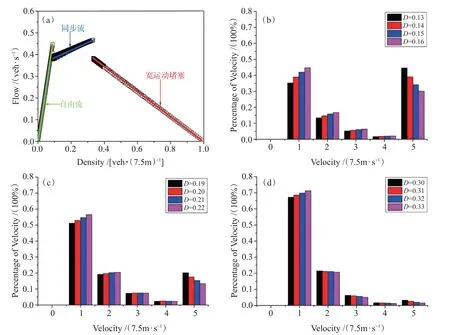
图1(a)均匀分布的基本图;(b)~(d)均匀分布下不同密度的速度分布

根据模型的更新规则,车间距影响车辆行驶速度,因此在探讨了密度对车辆速度的影响之后,进一步通过仿真实验研究密度和车间距之间的关系,更加细致地了解同步流的特性机理。仿真结果表明,在同步流区域内不同密度的车间距和车间距百分比值不同,两者的关系曲线大致分为以下两种。第一种情况是产生两个波峰。如图2(a)所示,第一个波峰是车间距等于1的时候,第二个波峰是车间距等于5的时候,其中,第一个波峰高于第二个波峰,即车间距等于1的百分比值大于车间距等于5的百分比值。交通流状态刚从自由流转到同步流时,当车密度较低,有一部分车辆依旧保持着最大速度v=5行驶,尽管道路中的车辆以p=0.5的概率进行慢化,仍然会有一定数量v=5的车辆没有慢化,根据模型演化规则的第2步和第3步,此时这部分的车间距最小为5,但是交通状态为同步流,车间距大于5的车辆较少,即v=5的车辆车间距为5的较多,故形成第二个波峰,如图2(a)所示。车间距等于1的车辆所占的百分比最高。第二种情况是只产生一个波峰,如图2(b)所示,模拟结果发现,同步流的密度越高,不同密度对应的曲线则趋于重合,有类似的统计分布规律。密度从D=0.2往后,只呈现一个波峰,如图2(c)所示,D=0.19时,车间距等于4(X所示)对应的百分比值低于车间距等于5(Y所示)所对应的百分比值;而D=0.2时,车间距等于4对应的百分比值高于车间距等于5对应的百分比值。

图2 车间距分布
2.2 致密分布
致密分布的基本图如图3(a)所示,其中,绿线表示自由流、蓝线表示同步流、红线表示宽运动堵塞。值得注意的是,致密分布下的同步流密度范围(图3(a))以及随机分布下的同步流密度范围(图3(b))相对于均匀分布下的同步流的密度范围(图1)较小。图4(a)与图1(b)的速度分布规律相似,当密度相对较低时,v=1、v=2、v=3所占据的百分比值随着密度的增加而明显增加,而v=4对应的百分比值增加的不明显;当密度相对较高时(D=0.2附近,和均匀分布下同步流高密度区间不同),v=1和v=2所占据的百分比值随着密度的增加而增加,v=3和v=4所占据的百分比值近似相等,如图4(b)所示。同时,v=5对应的百分比值随着密度的增加而减少。

图3(a)致密分布的基本图;(b)随机分布的基本图

图4 致密分布下不同密度的速度分布
同理,除了考虑密度对速度的影响,还需要讨论密度对车间距的影响,图5所示的车间距分布统计的仿真结果与图3类似,车间距和车间距百分比值的关系曲线同样分为两种,第一种是曲线呈现两个波峰;第二种是曲线呈现一个波峰。在同步流区域内,当车密度较低时,该曲线显示两个波峰,如图5(a)所示,其原因与均匀分布下的车间距和车间距百分比值关系曲线产生两个波峰原因是相同的。而在同步流区域内,当车密度较高时,该曲线呈现单峰状态,如图5(b)所示。

图5 车间距分布统计
2.3 随机分布
随机分布的基本图见上面图3(b)。在本文的更新规则下,致密分布和随机分布下不同密度的速度分布规律是相同的,分别如图4、图6所示。类似的,图7所示的车间距和车间距百分比值的关系曲线同样也是分为两种情况:在同步流密度相对较低的时候,曲线呈现双峰状态,如图7(a);同步流密度相对较高时,曲线呈现单峰状态,如图7(b)。曲线呈现双峰或者单峰的原因与致密分布类似,此处不再赘述。

图6 随机分布下不同密度的速度分布

图7 车间距分布统计
2.4 在相同密度不同初始分布下的速度和车间距分布比较
为了更好地了解密度对同步流的影响,这里将讨论固定密度下,不同初始分布的速度和车间距占据比值情况。图8所示的是在同步流区域内,相同密度下不同初始分布的速度分布比较,图8(a)、(b)、(c)对应的密度分别为D=0.13、D=0.17、D=0.21。结果发现:均匀分布、致密分布以及随机分布在相同的密度下,速度值所占的百分比值是非常接近的;随着密度的增加,这三种分布下的速度值v=1、v=2、v=3、v=4所占的百分比值也逐渐增加,而v=5所占的百分比值逐渐下降,如图8(a)、(b)、(c)所示。

图8 相同密度下的速度波动比较
除了考虑相同密度下不同初始分布对车辆速度的影响,还要讨论对车间距的影响。如图9所示,相同密度下的同一车间距所占的百分比值也非常接近,图9(a)、(b)、(c)对应的密度分别为D=0.16、D=0.19、D=0.22。随着密度的增加,车间距为1和车间距为2所占的百分比值明显增加,说明在同步流区域内道路上的车辆倾向于减小他们的车间距。

图9 相同密度下车间距比较
基于同步流状态下车辆速度和车间距分析,本文最后讨论这三种初始分布下模拟得到的车辆轨迹。如图10所示,处于同步流的图10(a)、(b)、(c)分别对应的初始分布为均匀分布、致密分布、随机分布,密度D=0.2,分别取第10辆车(th=10)、第20辆车(th=20)到第100辆车(th=100)的轨迹,轨迹线条的斜率越大,则速度越大。图中红色圆圈所示部分为v=5的车辆轨迹,并且维持了一定的时步,反映了三种初始分布下车辆间距Gap=5在道路中占据一定的比例,当密度小于0.2时,在车间距统计分布中Gap=5处产生第二个波峰,如图2(b)、图5(a)、图7(a)所示。与此同时,车辆的相对位置随着时步的增加忽大忽小,反映了车辆速度波动幅度范围较大。

图10 车辆轨迹
3 结论
综上所述,本文基于元胞自动机模型,研究了在同步流区域内均匀分布、致密分布以及随机分布在不同的密度下,车辆速度分布和车间距分布的统计特性。模拟结果表明,在三种初始条件分布下的同步流中,v=1对应的百分比值始终随着密度的增加而明显增加,而v=5对应的百分比值则随着密度的增加而减少。在同样的密度下,三种初始分布的速度占比近似相等。另外,三种初始条件分布下的车间距和车间距百分比值的关系曲线主要分为两种:在同步流区域内当车辆密度较低时,曲线呈双峰状态;当车辆密度较高时,曲线则呈单峰状态。同时也说明随着密度的增加,车辆趋向于减小他们的车间距。
