建筑垃圾在冲击荷载下的分形维数研究

裴 永， 李建军

(1. 山西省建筑科学研究院检测中心有限公司， 山西 太原 030001；2. 中北大学 理学院， 山西 太原 030051)

0 引 言

随着社会经济的发展和城镇化的深入推进， 固体废弃物产生量持续增加和处理能力相对滞后、 处理方式相对简单的矛盾日益凸显[1]. 大量建筑垃圾随意倾倒和掩埋， 这不仅给人民的生活和自然资源带来巨大危害， 而且造成了极大的资源浪费. 我国明确指出， 要从源头上控制与减少建筑垃圾的产生， 加快建设回收利用与消纳设施.

根据已有文献的报道， 建筑垃圾的利用和研究主要体现在以下方面： (1)研究再生粘土砖集料替代天然集料后， 再生混凝土的力学性能和耐久性方面受到的影响[2]； (2)再生集料应用于路基和路面基层或底基层填料方面的研究[3]. (3)利用建筑垃圾制备标准砖[4].

再生混凝土集料和再生粘土砖集料这两种材料的强度和物理性质相差较大， 二者在压碎过程中的相互干扰对集料破碎的影响还缺乏相关研究， 如何确定集料破碎过程中颗粒破碎的分形维数的影响因素是一个值得探讨的问题. 本文利用太原某高校教学楼的拆迁建筑垃圾对再生粘土砖和再生混凝土组成的再生混合集料(简称再生混合集料)进行了冲击破碎试验， 发现其破碎后的颗粒分布符合材料破碎的分形特征， 由此提出了由破碎试验颗粒分布确定再生混合集料分形维数的方法， 同时对试验结果进行一系列讨论. 在建筑垃圾的研究中， 集料的块度分布是集料破碎效果的重要依据， 因此分析建筑垃圾的分形维数是建筑垃圾回收再利用的重要环节， 而国内外最新文献中对建筑垃圾的分形维数的研究很少， 对建筑垃圾混合料的分形维数的研究更少.

破碎指标是研究颗粒破碎的首要工作之一. 颗粒破碎指标需意义明确， 能刻画颗粒破碎的程度， 并可进一步用于破碎规律的分析及本构模型的建立. 本文主要对不同击实功下， 粒径与分形维数之间的关系进行研究.

1 试验材料与方法

1.1 试验材料

破碎试验所用建筑垃圾取自山西太原某高校砖混结构拆迁楼. 对原始建筑垃圾去除筋材和杂质后， 按组分不同进行人工分拣， 选择出再生粘土砖块和再生混凝土块. 将再生粘土砖块和再生混凝土块分别通过鄂式破碎机(图 1 所示)进行机械破碎. 鄂式破碎机最大功率为3.5 kW， 进料粒径≤120 mm， 出料粒径为4 mm～45 mm.

(a) 拆迁建筑垃圾

对挑选后的建筑垃圾采用鄂式破碎机进行机械破碎， 并用标准方孔筛进行筛分， 分别制备粒径区间为19 mm～26.5 mm的再生混凝土集料、 再生砖集料和石灰岩样品. 通过规整仪去掉针状和片状颗粒， 置于烘干箱中维持100 ℃烘烤 3 h～4 h， 使集料处于完全失水干燥状态， 静置冷却后取出备用， 如图 2 所示.

(a) 再生混凝土集料

1.2 试验方案

选取干燥状态下的19 mm～26.5 mm的废弃混凝土集料与砖集料， 分别按照再生混凝土与再生粘土砖的质量比为0∶1, 4∶6, 6∶4, 8∶2, 1∶0 来制备混合集料试样， 同时制备同粒径区间天然石灰岩集料作为对比试样， 对每种试样进行3组平行冲击荷载试验， 试验工况分组见表 1. 试验前， 称量试样质量M0， 然后分3次将试样装入试筒中， 每次装入后均对试样表面整平并用金属棒的半球面端对其均匀捣实25次.

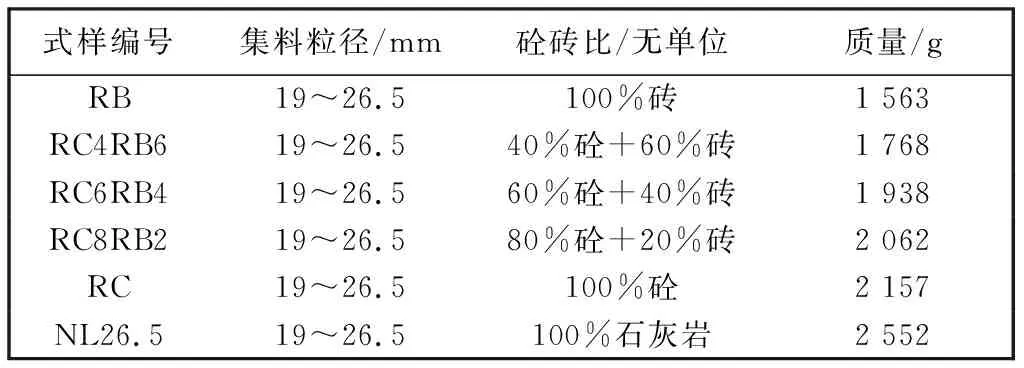
表 1 试验工况

本试验采用JDS-3型标准手提击实仪， 锤质量4.5 kg， 落高450 mm， 试筒内径Φ152 mm， 试筒高度127 mm， 填料高度100 mm. 将试筒放置在击实仪上， 对试筒进行固定， 然后依次对试样锤击 10次， 50次， 200次， 500次， 1 500次， 3 000次， 计算不同击实次数下的击实功Em分别为 0.109 J/cm3， 0.547 J/cm3， 2.188 J/cm3， 5.471 J/cm3， 16.413 J/cm3， 32.826 J/cm3， 对冲击破碎后的试样按孔径分别为19 mm， 16 mm， 13.2 mm， 9.5 mm， 4.75 mm和小于4.75 mm依次进行筛分和称重， 并对压碎后的粒径≥4.75 mm的混合集料进行人工分拣， 用电子天平分别称量各个粒径区间的再生混凝土和再生粘土砖集料.

图 3 为80%砼+20%砖经3 000击后通过标准筛筛分的过程及分拣结果.

图 3 80%砼+20%砖3 000击筛分过程

2 废弃混合料分形维数的确定

分形用于描述自然界的不光滑、 不规则、 不连续现象， 自Mandelbrot[5]提出分形几何的主要思想后， 分形广泛用于自然科学和社会科学的各个领域， 描述自然界的不规则、 不光滑程度的定量指标就是分形维数. 作为研究自然界中许多不规则现象和自相似现象的有效数学工具， 分形几何已对电化学[6]、 城市格局等领域产生了影响. 自1983年以来， Jevric等[7]将分形维数应用在岩石力学中， 用以研究地质结构、 岩石破裂以及岩石和土壤颗粒的表面、 孔隙度及接头粗糙度等. 平面空间是二维的， 而立体空间是三维的， 破碎后的颗粒相当于三维的空间中填充实体颗粒并存在许多孔隙， 因此， 实体颗粒在空间中一定是大于二维的平面空间且小于三维的立体空间.

1986年， Turcotte[8]对多种地质材料在不同的破碎方式下的碎块块度分布进行了统计分析， 得出其块度分布符合分形特征. Tyler等[9]在建立三维空间颗粒分形模型的基础上， 以颗粒质量代替体积， 推导出了以质量表示的分形维数方程. 徐永福等[10]根据颗粒破碎的分形维数导出材料的抗张强度公式， 并估算了给定压力下的破碎几率； 赵明华等[11]利用分形维数定量描述了红砂岩崩解破碎的非线性动态过程； 王益栋等[12]对大理岩汉白玉单颗粒材料进行破碎试验， 确定了颗粒破碎时变形与粒径间的关系， 并得到颗粒破碎的分形维数. 前人针对不同颗粒材料的分形研究均表明了材料破碎分形维数介于2～3之间， 其物理学含义为大于二维平面且小于三维空间的实体.

分形维数基本公式为

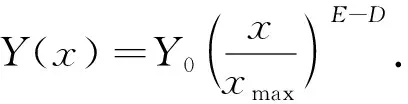
(1)

由式(1)可得小于某粒径di的集料体积为

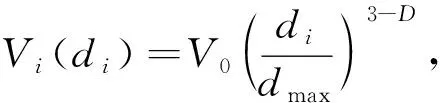
(2)

式中：V0为常数；D为分形维数；di(di>di+1)为标准方孔筛从上到下第i层筛孔孔径；dmax为集料中的最大粒径；Vi(di)为集料体积.

不同粒径集料密度相同， 小于某一粒径di的集料质量可表示为

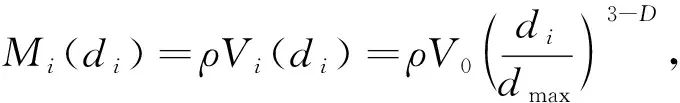
(3)

式中：Mi(di)为通过该层筛孔的集料的累计总质量。

令式(3)中di=dmax，则集料总质量M0可表示为

M0=ρV0.

(4)

将式(4)代入式(3)，可得

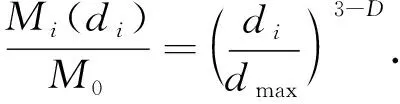
(5)

式(5)两边取对数，可得分形方程为

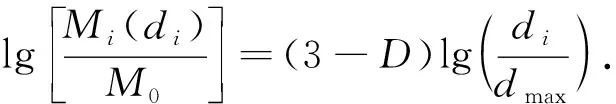
(6)

3 讨 论

3.1 破碎后的各级占比分析

经过大量试验研究发现， 随着击数的增加， 19 mm～26.5 mm粒径的集料逐渐减少. 由图 4～图 7 可直观看出， 4.75 mm～9.5 mm粒径的集料明显比其他粒径的集料多， 说明19 mm～26.5 mm粒径的集料起主要骨架的作用， 4.75 mm～9.5 mm粒径的集料起填充空隙的作用. 破碎后最大粒径相差0.22倍的粒径在级配中占比最大， 是最优填充粒径， 该结果与贝雷法[13]相同.

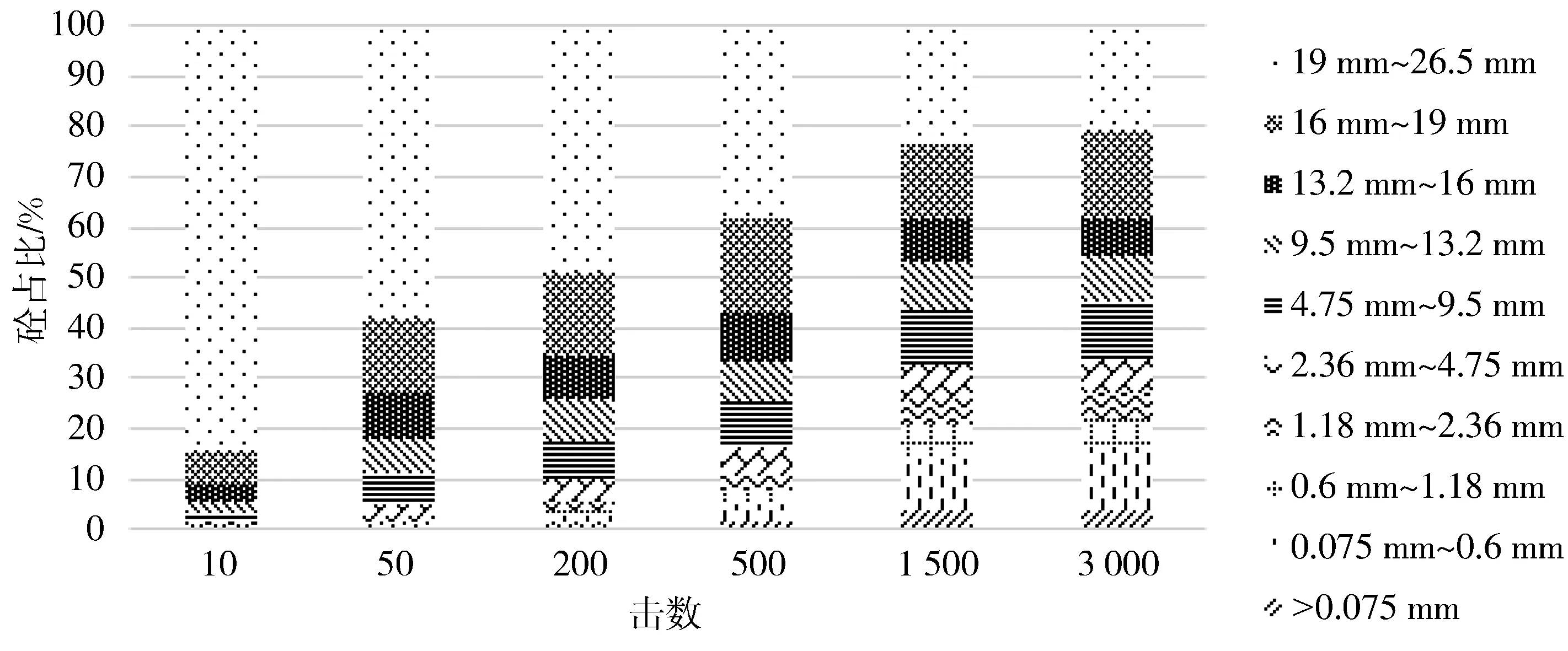
图 4 100%砼破碎后各级粒径集料占总质量的比例

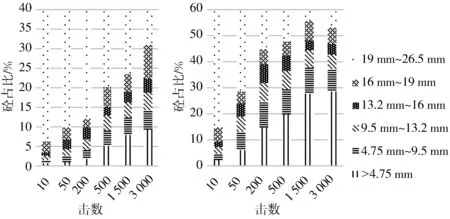
图 5 40%砼+60%砖破碎后各级粒径集料占总质量的比例

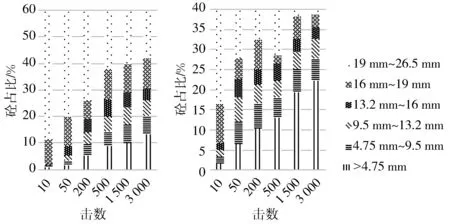
图 6 60%砼+40%砖破碎后各级粒径集料占总质量的比例

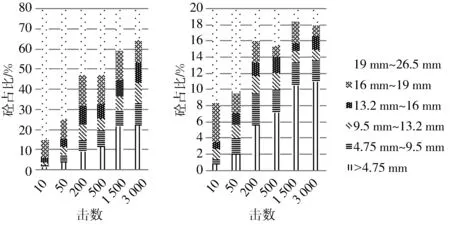
图 7 80%砼+20%砖破碎后各级粒径集料占总质量的比例

随着击数的增加， 细颗粒含量也在相对逐渐增加， 导致填充至粗颗粒形成的空隙中的细颗粒越来越多， 大孔隙逐渐转变为中小孔隙， 使得结构更加密实.

40%砼+60%砖从初始到3 000击的19 mm～26.55 mm砼的减少率为77.24%， 砖的减少率为88.54%.

60%砼+40%砖从初始到3 000击的19 mm～26.55 mm砼的减少率为70.04%， 砖的减少率为96.49%.

80%砼+20%砖从初始到3 000击的19 mm～26.55 mm砼的减少率为80.27%， 砖的减少率为89.75%.

由上述数据及图 5～图 7 可得， 两种强度明显不同的均匀粒径混合， 在冲击破碎时， 存在弃弱保强效应[14]， 强度大的得到较多保存， 强度小的优先破碎， 随着冲击能量的提高， 强度大的最大颗粒形成集料的空间骨架， 破碎的混合集料填充于空间骨架的空隙， 最终趋于分形分布， 构成密实级配， 结构最密实.

3.2 不同击数对分形维数的影响

由表 2 可知， 在相同配比条件下， 破碎集料的分形维数随击数的升高而升高， 即集料破坏程度随击数的升高越来越严重， 破碎颗粒中细颗粒数量越来越多. 在不同配比、 相同击数条件下， 分形维数： 砖>混合集料>砼>天然石灰岩. 由此可见， 分形维数不仅与外部因素有关， 而且与集料的本身强度也有关系.

表 2 不同击数下对应的分形维数

对比分形维数和破坏后的集料发现， 分形维数大的砖集料， 集料强度低， 破碎程度高， 块度均匀性好， 反之， 分形维数小的石灰岩集料， 集料强度高， 破碎程度相对较低， 块度均匀性差. 这进一步说明分形维能反映集料破碎的情况.

在冲击荷载作用下， 不同配比、 同一击数条件下， 随着砖掺量的降低， 分形维数逐渐降低. 但是， 在60%砼+40%砖到80%砼+20%砖的1 500击和3 000击分形维数的减少率分别为0.1%和0.43%， 由此可以预测60%砼+40%砖和80%砼+20%砖的破碎过程大致相同.

由表 2 可以得出， 随着击数的提高， 集料的分形维数不断增大， 在同一配比条件下， 较高击数(1 500击、 3 000击)集料的分形维数明显大于较低击数(50击、 200击)的破碎集料分形维数， 说明击数增加时， 集料破碎程度增大， 小粒径碎块比重增加， 碎块质量分布向小粒径端移动， 说明冲击功的增大导致集料趋于细粒化.

但是， 在80%砼+20%砖配比条件下， 1 500击和3 000击的分形维数相差不大， 3 000击的集料破碎后的分形维数相比1 500击的分形维数仅增加0.04%. 在60%砼+40%砖配比下， 3 000击的集料破碎后分形维数为2.576， 相比1 500击的集料破碎后的分形维数仅增加 0.39%. 由此可以判断， 80%砼+20%砖和60%砼+40%砖在3 000击时已经达到相对稳定状态.

3.3 相对破碎率与分形维数的关系

相对破碎率Br为破碎量Bt与破碎前的破碎势Bp的比值， 其中, 破碎势Bp为级配曲线与0.074 mm 粒径截断线所围成的面积A， 破碎量Bt为颗粒破碎前后的破碎势之差.

张季如等[15]通过石英粗砂和细砾的高应力侧限压缩试验， 得到Br与D存在较为显著的线性回归关系的结论.本文将初始分布均匀的废弃混凝土和废弃砖集料在同一配比、 不同击数试验下的相对破碎率Br和分形维数D采用直线回归方程进行拟合， 得到Br与D的关系如图 8 所示， 可以发现Br与D同样存在良好的线性关系， 拟合参数见表 3.

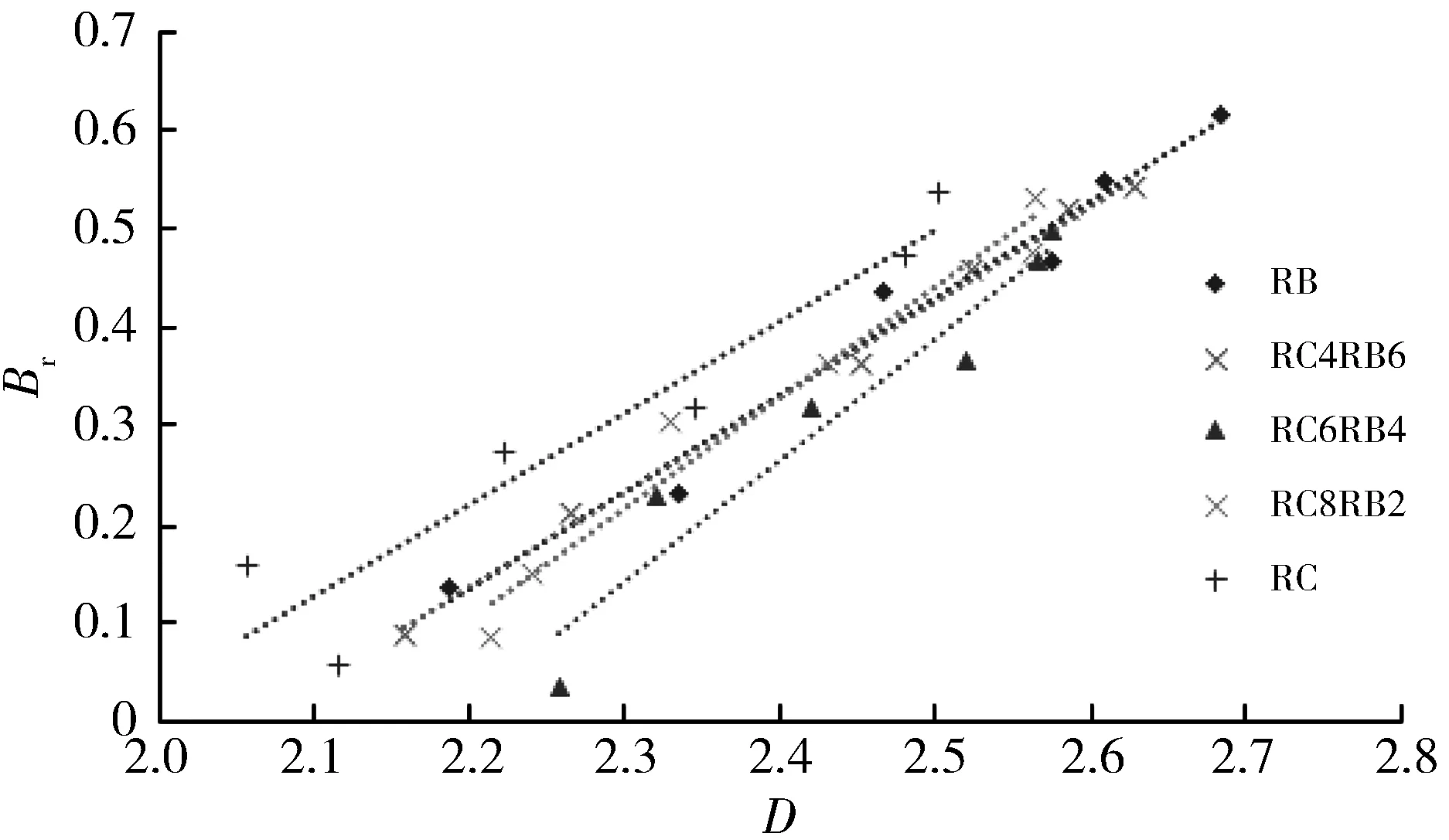
图 8 破碎指标分形维数D和相对破碎率Br的拟合

表 3 分形维数D和相对破碎率Br的拟合参数

由图 9 及拟合参数表 3 可以发现， 100%天然石灰岩的相对破碎率Br和分形维数D离散性较大， 相关系数为0.657. 主要原因是： 1) 天然石灰岩的强度高， 2) 天然石灰岩与建筑垃圾相比， 自身裂隙少， 结构致密. 因此， 3 000击不足以使天然石灰岩充分破碎， 才导致两者之间的相关系数较小， 这也进一步论证了D反映破碎量的可靠性. 同时， 说明在同一粒径的情况下，D和Br可以描述颗粒的破碎程度.

图 9 100%石灰岩破碎指标分形维数D和相对破碎率Br的拟合

综上所述， 对于初始分布均匀的废弃混凝土和废弃砖集料颗粒破碎有如下规律： 1) 相同级配， 不同击数条件下， 冲击能量越大， 相对破碎率越大. 2) 不同级配， 相同击数条件下， 相对破碎率的规律与分形维数规律类似， 相对破碎率顺序为砖>混合集料>砼>天然石灰岩. 3) 与天然石灰岩相比， 颗粒本身强度对破碎率有重要影响.

4 结 论

1) 初始分布均匀的废弃混凝土和废弃砖集料(19 mm～26.5 mm)在冲击荷载作用下， 破碎后的集料最大粒径相差0.22倍的粒径在级配中占比最大， 是最优填充粒径， 该结论与贝雷法相同.

2) 通过大量试验研究发现： 冲击能量对初始分布均匀的废弃混凝土和废弃砖集料(19 mm～26.5 mm)的破碎分形维数有影响， 随着冲击能量的增大， 集料的分形维数均有一定程度增加， 砖的增幅较大. 冲击能量相同， 分形维数为砖>混合集料>砼>天然石灰岩.

3) 初始分布均匀的废弃混凝土和废弃砖集料(19 mm～26.5 mm)在冲击荷载作用下， 分形维数大的砖集料， 破碎程度高， 碎块含量多， 破碎后的尺寸小； 分形维数小的石灰岩集料， 破碎程度相对较低， 碎块含量少， 破碎后的尺寸较大. 这说明分形维数能够反映集料的动态破碎情况， 分形维数与集料的强度呈反比关系.