基于正弦和拟合的太阳光追踪算法研究
2022-06-15冯程鹏穆继亮
邹 杰, 冯程鹏, 高 欣, 穆继亮
(1. 中北大学 仪器与电子学院, 山西 太原 030051;2. 中北大学 电子测试技术国防科技重点实验室, 山西 太原 030051)
0 引 言
社会的发展速度与能源的消耗速度成正比, 飞速发展的社会导致能源损耗日益增长, 不可再生资源的过度消耗必然会引起能源危机[1-2]. 为了解决这一问题, 世界各国都将新兴能源的开发作为首要任务. 目前, 新兴能源的种类主要有: 太阳能、 地热能、 风能和海洋能等[3-6]. 其中, 太阳能因其储量丰富、 分布广泛、 节能环保, 得到了各国广泛的关注与认可.
目前, 世界各国布放的太阳能电池板数量众多, 而太阳能电池板一般选择固定式朝南布放, 这种布放方式的太阳能转换效率比较低[7]. 为了最大化地提高太阳能的利用率, 太阳运动轨迹追踪成为了国内外科学家研究的重点与难点[8-14]. 国内外科学家对此做了很多研究, Cooper[15]、 Spencer[16]、 Stine[17]以及Bourges等[18]提出了赤纬角估算算法; Spencer[16]、 Stine[17]、 Whillier[19]、 于贺军等[20]提出了时差估算算法. 通过赤纬角与时差的估算算法, 太阳能电池板可以实时追踪到太阳的位置.
为了更高效地俘获太阳能, 本文提出了一种适用于赤纬角、 时差的估算算法——正弦和拟合算法. 此算法在传统算法的基础上, 研究了太阳运动轨迹的规律, 并以Matlab为计算仿真工具, 根据标准值来拟合年份与系数的对应关系, 以适用于所有年份太阳位置的追踪与计算. 此外, 选取2014年~2023年为样本时间, 将误差最大值、 误差均值、 均方根误差作为对比标准, 定量比较分析了正弦和拟合算法与传统算法之间的误差.
1 基础理论研究
1.1 太阳位置坐标系的选择
在太阳运动轨迹追踪的研究中, 由于太阳的位置是时刻变化的, 如果没有参照物, 很难精准地确定太阳位置变化的情况. 因此, 有必要选取一种坐标系作为太阳位置变化的参照物.
目前, 常用的天文坐标系主要有两种: 地平坐标系以及赤道坐标系, 如图 1 所示. 地平坐标系因其简便、 直接, 在现实生活中得到了广泛的应用. 如图 1(a) 所示, 观测人员通过地平坐标系能够很容易地追踪到太阳的运动轨迹, 因此, 本文选择地平坐标系作为追踪太阳位置的参考坐标系.
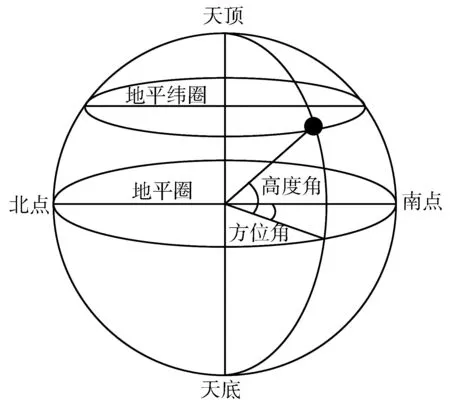
(a) 地平坐标系
1.2 太阳高度角与方位角的计算
由图1(a)可知, 在参考坐标系下, 太阳高度角与方位角成为了太阳运动轨迹追踪最关键的因素. 要实时、 精确追踪太阳位置, 必须通过算法精确估算出太阳高度角与方位角的值.
太阳高度角的计算公式为
sinα=sinφsinθ+cosφcosθcosω.
(1)
太阳方位角计算公式为
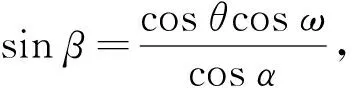
(2)
式中:α为太阳高度角;β为方位角;ω为时角;φ为当地纬度;θ为太阳赤纬角.
通过式(1)和式(2)可知, 太阳高度角与方位角只与赤纬角与时角有关(赤纬角与时角的相对位置如图 1(b) 所示). 因此, 要想准确地确定太阳的位置, 必须准确估算出赤纬角与时角. 太阳时角与真太阳时有关, 而真太阳时为平太阳时与时差的和. 其中, 平太阳时是人们日常生活所使用时间, 符合24 h的计时规律. 由此可得, 只要能够精确估算时差即可计算出太阳时角. 综上所述, 若想准确地追踪太阳的位置, 必须精确地计算出太阳的赤纬角与时差.
2 传统算法的研究
2.1 赤纬角计算及误差分析
在太阳运动轨迹追踪算法中, 赤纬角是一个非常重要的参数. 无论是高度角, 还是方位角, 都离不开赤纬角的精确估算. 典型传统赤纬角估算算法如下:
1) Cooper算法
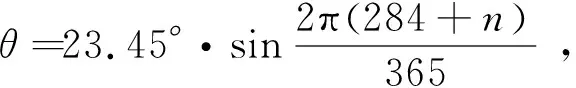
(3)
式中:n为日期序数, 比如: 1月5日,n=5.
2) Spencer算法
θ=0.070 257sinδ-0.399 912cosδ+
0.000 907sinδ-0.006 758cos 2δ+
0.001 48sin 3δ-0.002 679cos 3δ+0.006 918,
(4)
式中:δ为日角, 计算公式为
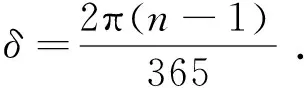
(5)
3) Stine算法

(6)
4) Bourges算法
θ=23.256 7sinδ-0.758cosδ+
0.114 9sin 2δ+0.356 5cos 2δ+
0.020 1cos 3δ-0.171 2sin 3δ+0.372 3,
(7)
其中,
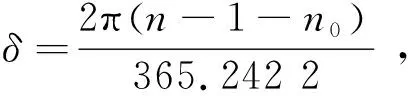
(8)
n0=0.242 2(m-1 969)-INT[0.25(m-
1 969)]+78.801,
(9)
式中:m为所求太阳位置的年份, 比如2018年1月9日,m=2018,n=9; INT为向下取整.
日梭万年历是世界上第一款采用现代高精度天文历算算法制作的四历对照、 信息丰富、 年代久远的万年历. 与同类型的万年历(中国天文年历、 国际著名的天体位置计算软件SkyMap Pro)相比较, 日棱万年历具有精度更高、 功能更全、 结果更值得信赖等优点, 是值得科研人员信赖的高精度万年历.

图 2 日梭万年历示意图
随机选取2018年~2019年为例, 以日梭万年历中的赤纬角为标准值, 以Matlab为计算仿真工具, 分别计算出Cooper, Spencer, Stine, Bourges 4种传统算法的估算值, 通过对比4种算法的误差最大值、 误差均值以及均方根误差来衡量算法的精准度. 对比结果如表 1, 表 2 所示.
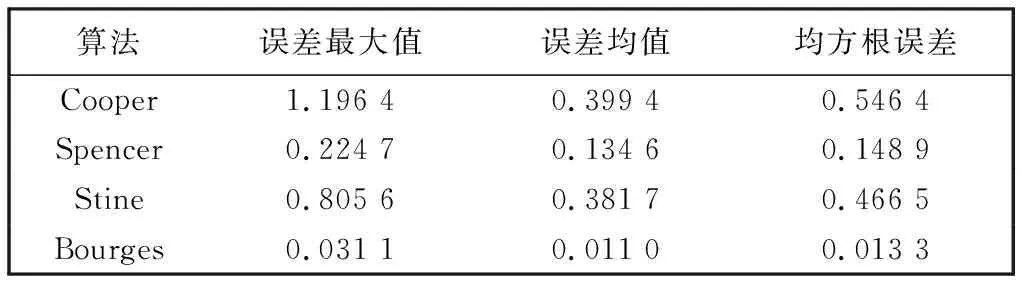
表 1 2018年赤纬角误差分析
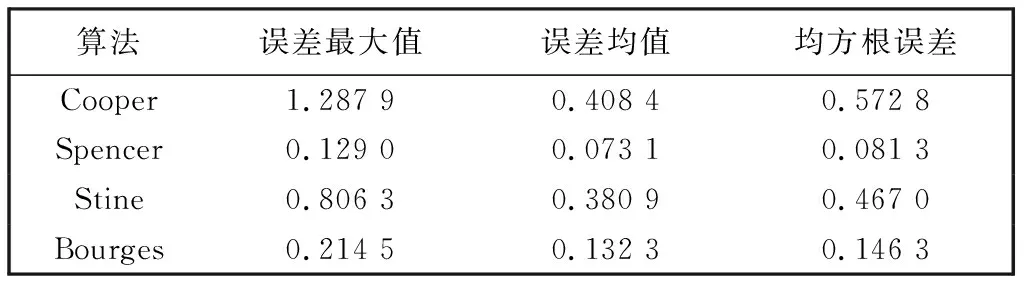
表 2 2019年赤纬角误差分析
在上述4种赤纬角估算算法中, Bourges算法在2018年中的估算误差较小, Spencer算法在2019年中的估算误差较小, 而Cooper算法与Stine算法在两年期间的误差都比较大. 由此可见, 传统算法中并没有一种适用于所有年份且计算精度精确的赤纬角估算算法.
2.2 时差计算及误差分析
由1.2可知, 时差补偿是否精确直接影响到太阳位置追踪的准确性. 因此, 研究出一种精确的时差估算方法尤为重要. 下面介绍几种传统的时差估算算法:
1) Spencer算法
ω=(0.001 868cosθ-0.032 077sinθ-
0.014 615cos 2θ-0.040 89sin 2θ+
0.000 075)·229.18,
(10)
其中,
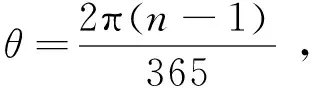
(11)
式中:n为日期序数, 比如: 1月5日,n=5.
2) Stine算法
ω=0.258cosθ-7.416sinθ-
3.648cos 2θ-9.228sin 2θ,
(12)
其中,
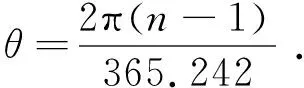
(13)
3) Whillier算法
ω=9.87sin 2θ-7.53cosθ-1.5sinθ.
(14)
其中,
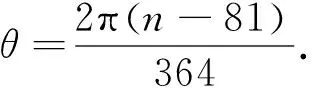
(15)
4) Yu算法
ω=0.428 1cosθ-7.351 5sinθ-
3.349 5cos 2θ-9.361 9sin 2θ+0.017 2,
(16)
其中,
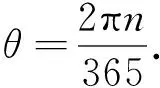
(17)
随机选取2018年~2019年为例, 以日梭万年历中的时差为标准值, 以Matlab为计算仿真工具, 分别计算出Spencer, Stine, Whillier, Yu 4种传统算法的估算值, 通过对比4种算法的误差最大值、 误差均值以及均方根误差来衡量算法的精准度. 对比结果如表 3, 表 4 所示.
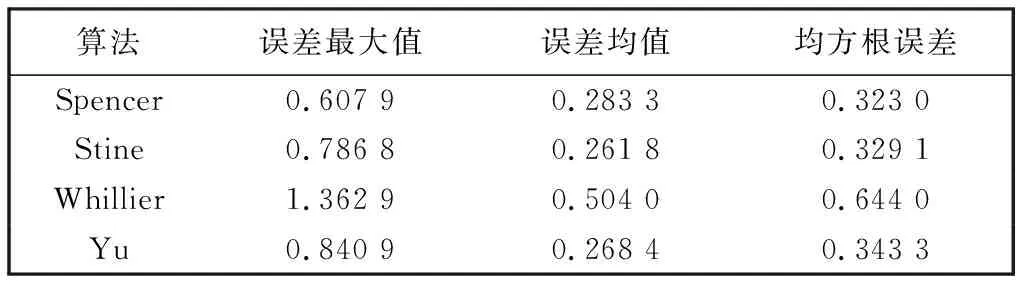
表 3 2018年时角误差分析
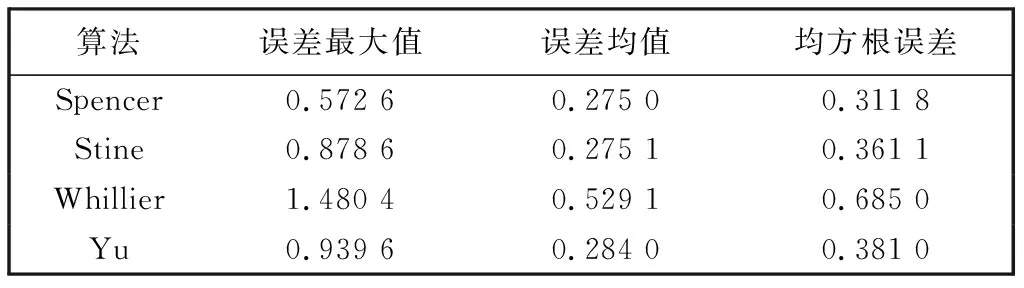
表 4 2019年时角误差分析
在上述4种时差估算算法中, 虽然Spencer算法误差最小, 但是它仍没有达到一个理想的计算精度. 由此可见, 传统算法中并没有一种适用于所有年份且计算精度精确的时差估算算法.
3 正弦和拟合算法
上述4种传统算法在计算不同年份太阳位置时采用相同的系数, 并未考虑不同年份太阳位置的变化带来的差异, 因此, 随着年份的不同, 各种算法的误差也不尽相同. 本文算法在保持算法计算简便的同时, 以精确估算太阳赤纬角与时差为目的, 提出一种针对不同年份可以调整相关系数的正弦和拟合算法.
以2020年为例: 首先, 将日梭万年历中的赤纬角与时差信息作为标准值, 通过Matlab计算仿真拟合出2020年太阳赤纬角与时差的标准曲线. 标准曲线如图 3 所示.
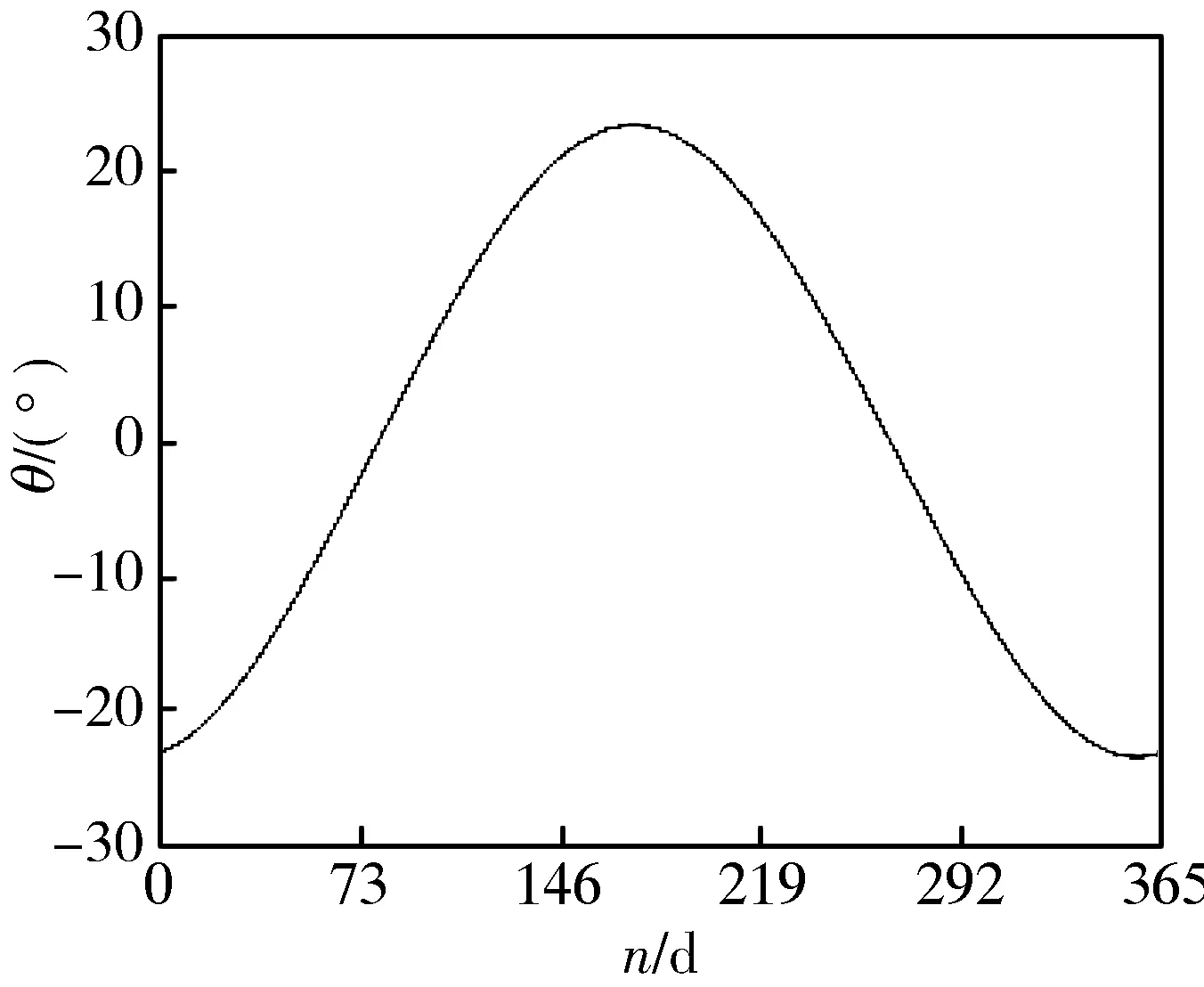
(a) 2020年太阳赤纬角
其次, 分析太阳赤纬角与时差的标准曲线, 确定太阳运动轨迹追踪算法(正弦和拟合算法), 计算公式为
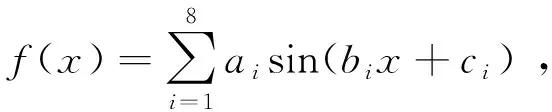
(18)
式中:x为日期序数, 比如2020年1月5日, 表示2020年的第5天, 此时x=5;i为拟合阶数, 其与计算精度有关.拟合阶数越高, 拟合曲线越贴近实际测量点, 但拟合阶数过高, 会使整个算法的计算量增大, 效率不高.本文中选取的拟合阶数(i=8)是两者综合考虑的结果.
最后, 根据上述正弦和拟合算法公式, 在Matlab中进行编程, 最终得到了2020年的太阳赤纬角以及时差的拟合系数, 如表 5 所示.
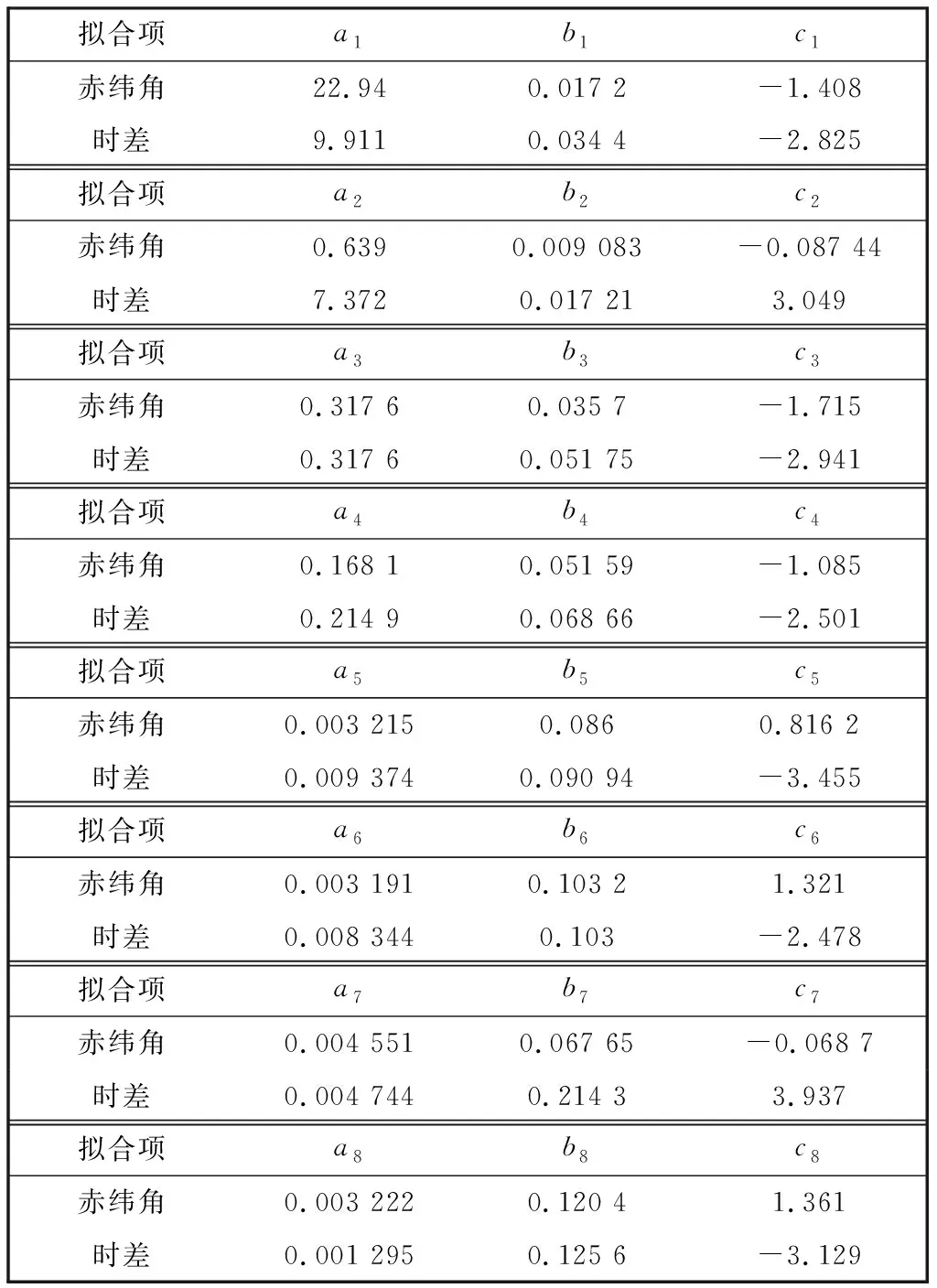
表 5 2020年太阳赤纬角与时差算法的拟合系数
为了更直观地体现正弦和拟合算法与传统算法误差的对比, 本文选取了2020年~2023年为样本时间, 将日梭万年历的值作为标准值, 应用Matlab仿真工具对传统算法和正弦和拟合算法误差进行对比, 结果如图 4 所示.
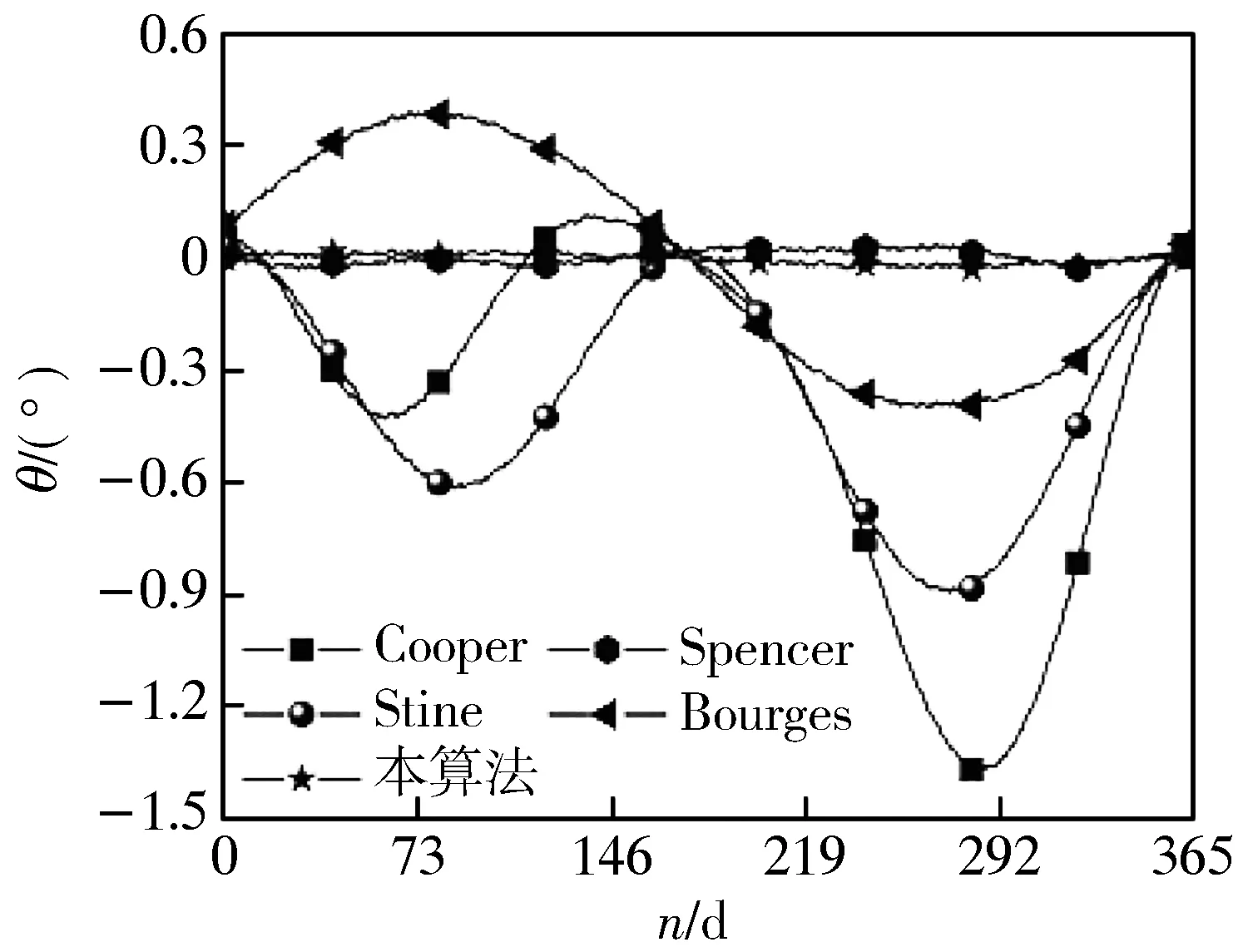
(a) 2020年太阳赤纬角误差
图 4(a)~图4(d)为太阳赤纬角的误差对比图. 不同形状的散点图代表不同算法的预测值与标准值的差值, 曲线波动范围越大, 证明算法的误差越大; 曲线平稳且在0附近波动, 证明算法误差越小. 从图中可以看出: 在2020年~2023年期间, Cooper算法与Stine算法的曲线波动范围很大, 最大的误差值甚至超过了1°; Spencer算法与Bourges算法在某些年份曲线平稳且误差值接近于0, 但在某些年份误差最大值几乎达到0.5°, 由此证明这两种算法并不适用于所有年份; 本文所提出的正弦和拟合算法, 4年期间曲线波动范围较小, 误差值近似为0, 适用于所有年份且计算精度优于传统算法.
图 4(e)~图 4(h)为太阳时差的误差对比图. 从图中可以看出, 在2020年~2023年期间, Spencer算法、 Stine算法、 Whillier算法和Yu算法的曲线波动范围都比较大, 尤其是Whillier算法, 最大误差值超过了1.5 min; 本文提出的正弦和拟合算法, 4年期间误差曲线波动范围很小, 误差值近似为0, 适用于所有年份且计算精度优于传统算法.
为了定量描述传统算法与本文算法(正弦和拟合算法)的差别, 选取2014年~2023年为时间样本, 通过误差最大值、 误差均值、 均方根误差对上述几种算法进行误差分析. 图 5(a)~图 5(c)为赤纬角的计算误差分析. Cooper算法、 Stine算法、 Spencer算法、 Bourges算法、 正弦和拟合算法每天的误差分别为0.406°, 0.106°, 0.133°, 0.008°, 本算法的误差远远小于其他算法. 均方根误差反映了预测值与标准值之间的偏离程度, 其中Cooper算法、 Stine算法的均方根误差均控制在10-1量级; Spencer算法与Bourges算法都是以4年为一个周期, Spencer算法在闰年的均方根误差控制在10-3量级; Bourges算法在4年中的某两年均方根误差控制在10-3量级; 本文提出的正弦和拟合算法, 它的均方根误差可以平稳地控制在10-3量级, 相比于传统算法的均方根误差, 至少提高了一个数量级, 由此证明了正弦和拟合算法在估算赤纬角时优于传统算法.
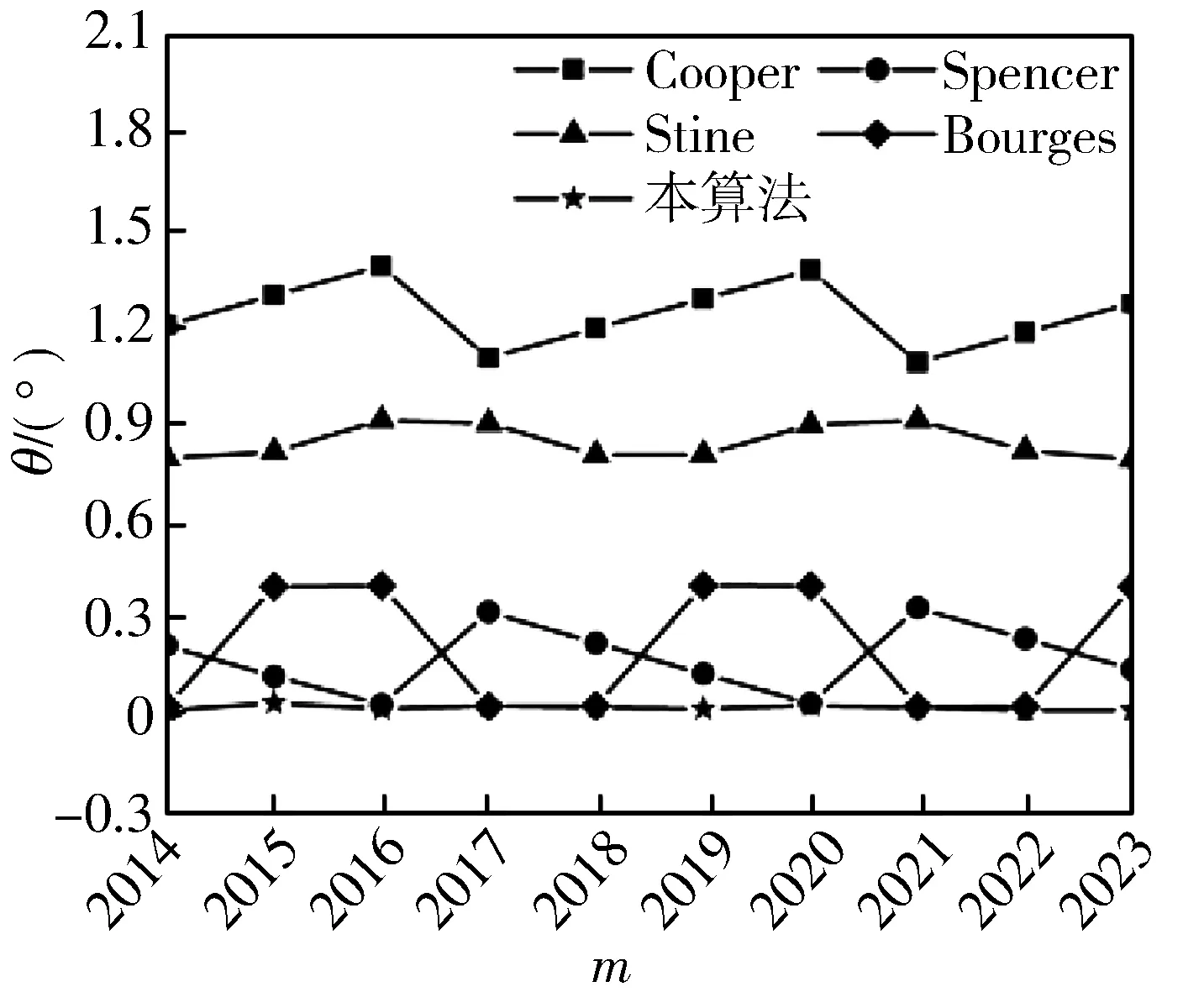
(a) 赤纬角误差最大值
图 5(d)~图 5(f)为时差的计算误差分析. 从图中可以看出, Spencer算法、 Stine算法、 Whillier算法、 Yu算法10年内每天的误差分别为0.281 min, 0.271 min, 0.520 min, 0.279 min, 且均方根误差在10-1量级; 本文提出的正弦和拟合算法, 10年内每天的误差为0.007 min, 均方根误差控制在10-3量级, 改进效果非常显著.
4 实验验证
为了验证正弦和拟合算法的估算效果, 本文选取传统算法中精确度较高的Spencer算法与正弦和拟合算法进行比较. 在自然光照下, 分别将使用两种算法的追光系统放置于空旷地带, 追光系统上的太阳能电池板通过BQ25570电源管理芯片给200 mAh的锂电池充电, 每隔一段时间测量一次锂电池的电压. 图 6 为使用不同算法的追光系统给锂电池充电的曲线图. 从图中可以看出, 无论是晴天还是阴天, 使用正弦和拟合算法的追光系统的锂电池蓄电量更多. 由此可得, 正弦和拟合算法的使用提高了追光系统对于太阳光的追踪精度, 提升了太阳光的利用效率, 具有非常广阔的应用前景.
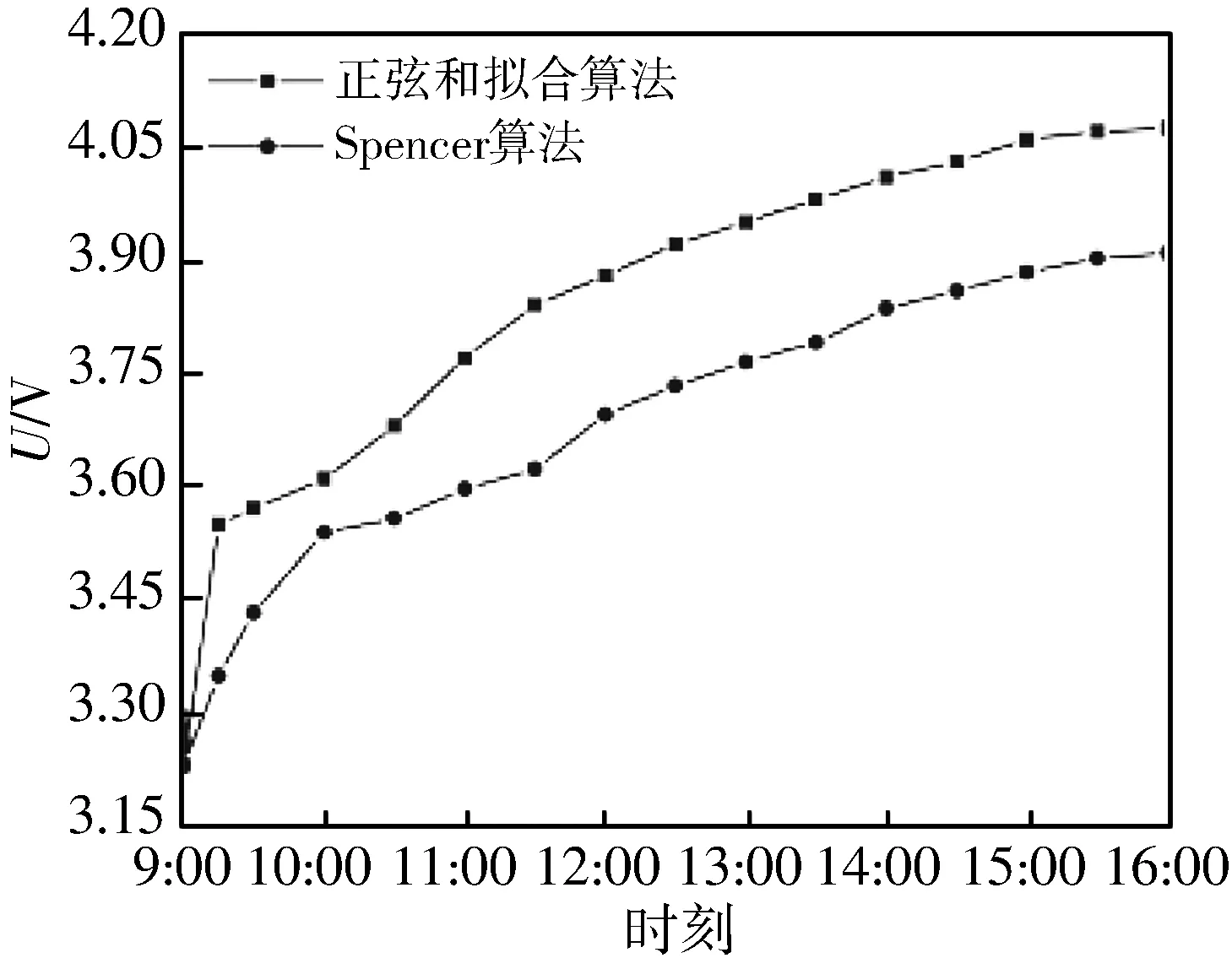
(a) 晴天
5 结 论
本文以太阳运动轨迹追踪算法为研究对象, 提出了一种太阳位置估算算法——正弦和拟合算法. 在传统算法的基础上, 利用Matlab作为计算仿真工具, 日梭万年历的角度作为标准值. 选取了2014年~2023年为样本时间, 对传统算法与本文算法进行了误差分析, 得出以下结论:
1) 传统赤纬角估算算法的最小误差均值为0.106°, 传统时差估算算法的最小误差均值为0.271 min, 而正弦和拟合算法的误差均值分别为0.008°, 0.007 min.
2) 无论是赤纬角估算算法, 还是时差估算算法, 传统算法的误差均方根均在10-1量级, 而正弦和拟合算法的均方根误差可以控制在10-3量级, 计算精度提高了两个数量级.
3) 在同样的条件下, 应用正弦和拟合算法的追光系统与应用传统算法的追光系统相比, 前者具有更强的能量收集能力.
4) 正弦和拟合算法在计算精度、 适用性方面优于传统算法. 正弦和拟合算法在精准追踪太阳位置、 提高太阳能的利用效率方面具有较高的实用价值.
