改进小波神经网络在弹丸落点预报中的应用

赵归平， 陈国光， 闫小龙， 董晓芬， 张 斌

(1. 中北大学 机电工程学院， 山西 太原 030051； 2. 中国兵器工业第五九研究所， 重庆 400039)

0 引 言

在现代战争中， 传统弹药早已无法适应作战需要. 与导弹相比， 制导弹药的成本较低， 且能满足现代常规作战的需要， 因此制导导弹已经成为弹药的重点发展方向之一. 其中， 弹丸落点的预测是否准确是影响制导弹药是否可以精确打击目标的关键因素. 目前， 国内外对于弹道的落点预报使用的方法主要有4种： 第一种方法是通过四阶龙格库塔方法解算六自由度弹道方程， 获得解析解[1]； 第二种方法是将六自由度非线性弹道方程线性化处理之后将其作为状态方程， 然后利用卡尔曼滤波等方法推导出落点位置[2]； 第三种方法是先对六自由弹道的诸元进行辨识之后， 再通过扩展卡尔曼滤波或者无迹卡尔曼滤波等方法进行外推落点[3]； 第四种方法是将人工智能算法应用在落点预测中， 主要有遗传算法和神经网络算法[4]等. 但是， 这些算法的缺点在于需要大量的样本对其进行训练， 且实时性不能满足要求.

针对以上方法的不足， 学者们提出了许多改进方法. 史金光等[2]对外推弹道模型进行了解算与分析， 利用扩展卡尔曼滤波方法对弹道进行参数辨识， 建立了该方法对应的弹道模型， 对侦察雷达测到的弹道参数进行卡尔曼滤波滤除噪声， 快速地减小了噪声， 提高了外推弹道的落点精度； 李志鹏等[4]利用改进BP神经网络算法来对弹丸进行落点预测， 使用 4层网络结构进行样本训练， 即并列隐含层的双隐层结构， 通过改进动量因子， 选择并优化了训练样本， 极大地提高了预测精度； 何光林等[5]利用GPS原理进行落点预测， 采用最小二乘拟合弹道， 并对弹道误差进行补偿， 大大降低了预报落点的偏差， 提高了预报精度； 田再克等[6]设计了一款摄动制导系统， 利用GPS对弹丸进行落点预测， 根据基准弹道获取足够多的样本点, 基于摄动原理并应用多项式拟合的方法建立预报模型， 通过仿真验证得到比例系数k， 在弹载计算机中装定比例系数， 使得弹丸在飞行中可实时预测， 该系统利用摄动原理提高了弹道修正弹的落点精度.

与传统的数值积分方法相比， 上述方法在解算精度低、 容错机制差和实时性差等方面均取得了一些突破， 但仍存在一些缺陷， 如： 滤波外推法处理非高斯噪声时容易发散， 线性化法精度不足等. 本文针对这些缺陷， 利用布谷鸟算法收敛速度快、 精度高和小波理论在信号提取和分析方面的优势， 提出了一种用布谷鸟算法改进小波神经网络的落点预报方法.

1 改进小波神经网络

1.1 CS算法改进小波神经网络

CS算法是基于布谷鸟借巢产卵的行为和列维飞行的行为模拟出来的， 可避免陷入局部极小值点， 具有很好的全局优化性能. 优化WNN的实质是对其初始参数进行优化， 这是因为神经网络的初始参数在大多数情况下使用随机数来确定， 具有很多的不确定性， 导致训练结果时好时坏， 有时还会有无法收敛的可能.

针对此类问题， 利用布谷鸟算法预测精度高和收敛速度快的优势， 可有效地对WNN进行优化. 先确定基于产卵行为和列维飞行的布谷鸟巢位置更新公式为

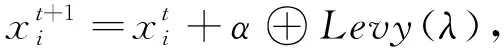
(1)

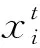
接着， 确定适应度函数， 设定训练期望值， 将期望值与实际值的总误差函数作为CS算法的目标函数. 通过布谷鸟算法的训练， 确定一组最优权重参数[7]， 然后将这组值代入落点预报函数中， 进行仿真分析. 这种算法的目标函数E为

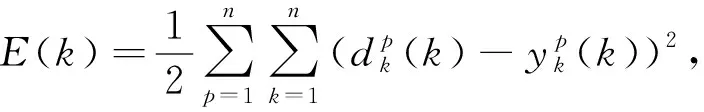
(2)

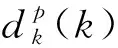
1.2 APSO改进小波神经网络

粒子群方法可以解决神经网络收敛速度慢的问题， 且搜索能力强， 但存在搜索精度不足、 特别容易陷入局部极值、 容易早熟收敛等问题， 可利用惯性权重来达到平衡搜索能力的目的. 惯性权重ω影响的是粒子的速度， 每进行一次迭代就会影响一次粒子速度， 且取值与粒子的全局寻优能力具有正相关关系. 当取值为1时， 就为传统PSO算法. 用APSO方法对WNN网络的初始参数进行优化， 可提高落点预报的精度和收敛速度. 采用动态惯性权重法， 即

ω=0.5+rand()/2，

(3)

则粒子速度ω更新公式为

vid(t+1)=ω×vid(t)+c1rand1()×

(pid-xid(t))+c2rand2()×(pgd-xid(t)),

(4)

式中： rand1()， rand2()为[0,1]的随机数；c1，c2为学习因子.

1.3 训练流程

根据WNN的训练流程[8-9]， 本文提出的布谷鸟优化WNN的流程如下：

Step1： 建立网络模型并初始化其参数， 即初始化鸟巢的位置.

Step2： 加载弹道数据训练样本. 训练前， 要对初始数据进行归一， 然后加载到目标函数中， 计算每个鸟窝的适应度值.

Step3： 寻找最小误差函数值. 确定好训练误差后， 根据设定值判断是否满足误差要求. 若符合设定的误差条件， 即可跳出循环， 完成训练， 转至最后一步； 反之， 如果不符合误差条件， 则进行第4步.

Step4： 更新鸟巢位置. 更新次数由最大迭代次数决定， 若达到， 则再循环一次程序即可终止， 否则， 返回上一步.

Step5： 网络调试. 对已经完成训练的样本求解预测误差， 如果达到程序终止条件， 即可导出网络参数， 否则调整当前网络参数值， 开始重新训练. 流程图如图 1 所示.

图 1 改进算法流程图

2 小波神经网络的弹丸落点预报模型

2.1 落点预报非线性数学模型

落点预报是制导弹药精确打击目标的关键技术之一， 可通过提高预报的精度来减小弹丸修正的偏差[10]. 从图 1 可知， 输入与输出信号之间存在简单的线性叠加关系， 即简单的函数进行多次线性叠加. 这个结构可以理解为函数的自变量经过相应的法则运算可得到因变量， 隐含层就是自变量与因变量的对应关系.

本文是在标准大气条件下， 训练出一条基准弹道， 通过比较预测结果与基准弹道的差值来说明改进WNN在落点预报时的准确性， 仿真的预测误差值越小越好. 在实际应用中， 必须先对实际气象条件与标淮气象条件的偏差进行修正. 根据计算的6D刚体弹道方程组， 构建落点与任一组弹道诸元之间的非线性关系， 用到的诸元主要有速度矢量、 位置矢量和姿态角. 姿态角指的是俯仰角和偏航角[11]， 且可在弹道解算时得到， 其数学模型的形式为[12～16]

A=f(B)，

(5)

式中：A为落点信息， 即射程和横偏；B为弹丸的任一组弹道参数.

射程和横偏落点预报非线性数学模型可表示为

(6)

式中：x,y,z,vx,vy,vz分别为弹丸位置三分量及速度三分量；θ,ψ分别是俯仰角和偏航角，X,Z为射程和横偏.

2.2 落点预报WNN拓扑结构

根据数学模型的特点， 建立单隐含层双输出的三层网络结构. 由式(6)可知： 与横偏和射程有关的自变量共有8个， 可根据自变量的数目确定输入层神经元的个数为8； 此结构只有一个隐含层， 其神经元的数量也为8； 输出层神经元个数为2. 最终确定射程和横偏预报的WNN拓扑结构如图 2 所示.

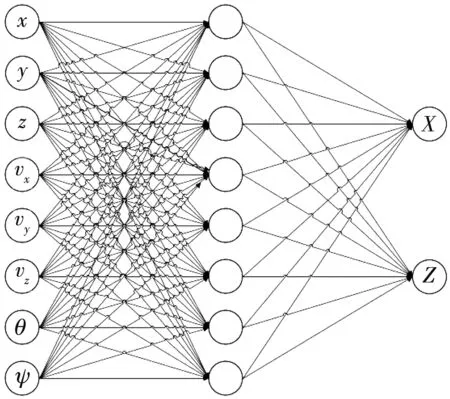
图 2 落点预报网络拓扑图

数据量纲不一致、 范围不尽相同是导致数值差异过大的根本原因， 这使得权重无法起到很好的调节作用， 会直接影响最后的分析结果. 鉴于此， 可以将待训练的弹道参数样本点进行归一化处理. 对数据进行归一化的实质是进行数据缩放， 从而可改变其范围. 弹道数据的范围大， 为保证数据处理后可得到精确合理的基准弹道， 应在弹道的各个阶段均选用适量的数据点， 运用min-max标准化方法， 将数据调整到[0,1]之间. 转化公式为

(7)

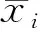
3 仿真分析

3.1 落点预报准确性分析

本文所提出的落点预报研究对象为某型号火箭弹. 通过解算弹道方程可得到弹道数据， 采用均匀抽样的方法， 抽取最大射程角为51°时的500组弹道数据， 前450组数据作为训练样本， 后50组作为预测样本； 每组数据都有8个， 分别是位置三分量、 速度三分量和姿态角. 假设鸟巢数为15个， 鸟蛋被巢主发现的概率为0.25， 粒子群种群数为70， 学习因子c1和c2均为2， 惯性权重为0.5， 最高迭代次数为200， 空间维数为70， 学习精度为1×10-6m2， 基于MATLAB平台进行预报仿真. 训练结果如图 3 和图 4 所示. 图 3 为两种方法的射程预报误差对比图， 射程预报误差指的是预报落点与基准弹道落点之间的纵向差值.

图 3 射角为51°时的射程预报误差Fig.3 Schematic diagram of range prediction error in fire angle of 51°

图 4 为两种方法的横偏预报误差对比图， 指的是预报落点与基准弹道落点之间的横向差值.

由图 3 和图 4 可得： 采用CS-WNN方法的射程预报误差值的绝对值最大为0.000 501 m， 最小为0.000 272 m； 横偏预报误差值的绝对值最大为0.011 71 m， 最小为 0.001 01 m. 采用APSO-WNN方法的射程预报误差值的绝对值最大为 0.0001 561 m， 最小为 0.000 821 m； 横偏预报误差值的绝对值最大为 0.035 62 m， 最小为 0.002 98 m. 可以看出， 使用CS-WNN方法的射程预报误差值约为APSO-WNN方法的1/3， 横偏预报误差约为APSO-WNN方法的1/2， 说明CS-WNN方法的精度更高.

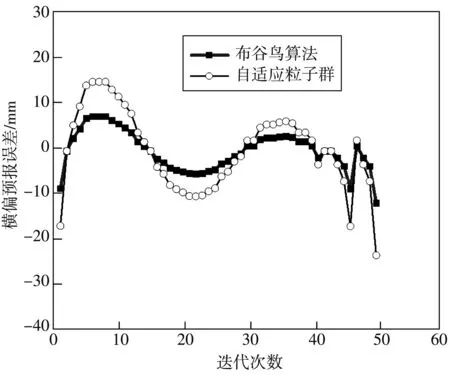
图 4 射角为51°时的横偏预报误差Fig.4 Schematic diagram of transverse prediction error in fire angle of 51°

3.2 落点预报快速性分析

选用射角为51°时的离线训练数据， 将满足预报精度的网络参数(权值及平移、 伸缩因子)导入到预测模型中， 可装载在DSP中用于落点预报. 由于弹箭的飞行速度快， 飞行时长一般在60 s～120 s， 其预报的快速性必须得到保证， 因此， 分别对两种方法进行落点预报的快速性分析， 结果如表 1 和表 2 所示.

由表 1， 表 2 可知， 使用CS-WNN方法射程预报计算的时间为0.341 4 ms， 横偏预报计算的时间为0.379 8 ms， 总预测时间为0.721 2 ms； 使用APSO-WNN方法射程预报计算的时间为 0.565 4 ms， 横偏预报计算的时间为0.577 8 ms， 总预测时间为1.143 2 ms， 后者几乎是前者的 1.5倍. 落点预报仿真结果表明， 用CS-WNN方法进行落点预报具有更快的速度.

表 1 基于CS-WNN的弹丸落点预报时间

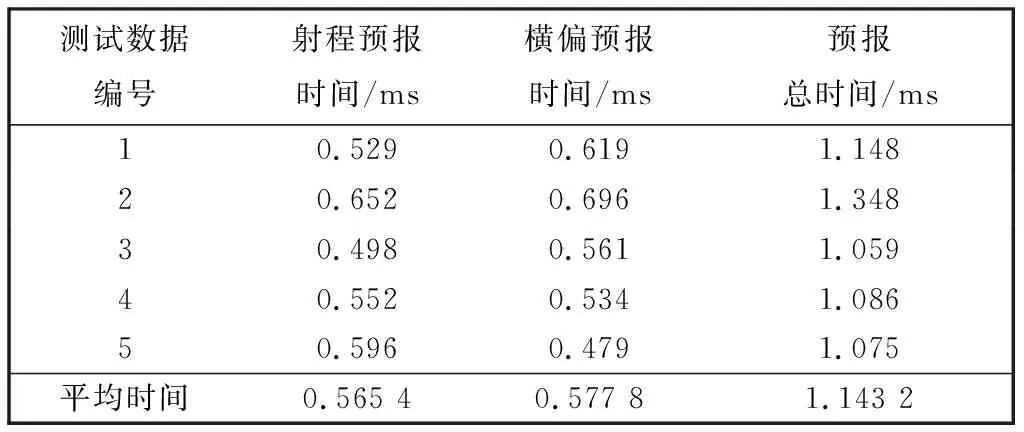
表 2 基于APSO-WNN的弹丸落点预报时间

3.3 落点预报普遍适应性分析

3.1节和3.2节主要是对射角为51°时的弹道落点用两种方法进行了预报， 并对比了两种方法的优劣， 但根据作战需求和地理环境的影响， 作战人员会根据实际情况调整射角. 因此， 需要对不同的射角进行落点预报仿真， 以证明此算法普遍适应性. 分别抽取射角为30°， 35°和40°的弹道数据500组， 用CS-WNN方法进行落点预报， 前450组作为训练样本， 后50组作为预测样本. 参数设置与射角为51°时的相同. 训练结果如图 5 和图 6 所示.

图 5 不同射角时的射程预报误差Fig.5 Schematic diagram of range prediction error in different angle of fire

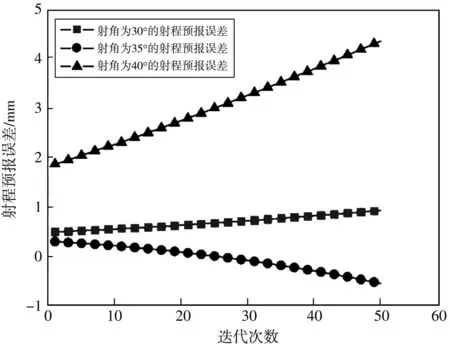
图 6 不同射角时的横偏预报误差Fig.6 Schematic diagram of transverse prediction error in different angle of fire

由图 5 和图 6 可得： 当射角为30°时， 射程预报误差值的绝对值最大为0.014 03 m， 最小为0.003 98 m； 当射角为35°时， 射程预报误差值的绝对值最大为0.001 32 m， 最小为 0.000 559 m； 当射角为40°时， 射程预报误差值的绝对值最大为0.001 47 m， 最小为 0.000 922 m； 当射角为30°时， 横偏预报误差值的绝对值最大为0.000 589 m， 最小为 0.000 114 m； 当射角为35°时， 横偏预报误差值的绝对值最大为0.001 02 m， 最小为 0.000 101 m； 当射角为40°时， 横偏预报误差值的绝对值最大为0.004 32 m， 最小为 0.001 61 m. 以上结果表明， 该算法在射角为30°～51°范围内时满足准确性要求 ， 可为工程应用提供理论依据.

分别对上述3个射角进行5次落点时间预报， 结果如表 3 所示.

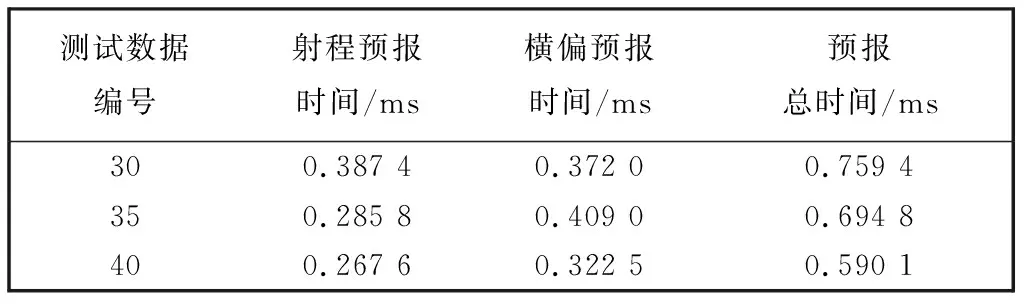
表 3 射角为30°， 35°和40°时的弹丸落点预报时间

由表 3 可知： 射角为30°时， 总预报时间为 0.759 4 ms； 射角为35°时， 总预报时间为 0.694 8 ms； 射角为40°时， 总预报时间为0.590 1 ms. 这些与射角为51°时的总预报时间相差不大， 均小于1 ms. 结果表明， 该算法在射角为 30°～51°时均适用， 能满足弹丸落点预报的快速性和准确性的要求.

4 结束语

针对弹丸落点预报出现的无法收敛以及收敛速度慢等问题， 提出了用CS算法来训练落点预报初始参数， 利用CS算法全局搜索和快速收敛能力强的特点， 提升了落点预报的精度和速度. 本文从建立落点预报的非线性数学模型出发， 构建网络结构， 从落点预报的准确性、 快速性和普遍适应性三方面对算法进行了验证， 并对两种方法的预报结果进行了分析对比. 结果表明， 相比APSO方法， 本文利用布谷鸟算法优化后的WNN算法在精度和解算时长方面更能满足落点实时预报的要求.