火箭子母弹对机场跑道毁伤封锁概率的研究

肖艳文， 李 强， 郭向向

(1. 中国人民解放军32381部队， 北京 100071； 2. 中北大学 机电工程学院， 山西 太原 030051；3. 山东特种工业集团有限公司， 山东 淄博 255201)

0 引 言

现代军事战役中， 能否夺取和保持制空权， 对战役的成败具有决定性影响. 而夺取制空权， 需要针对机场、 防空阵地等设施进行有效毁伤， 其中机场跑道面积较大， 缺乏有效的防护， 相对易于毁伤. 如果能够通过破坏机场跑道道面， 在一定时间内形成对敌方飞机起降的封锁， 则可为我方战术行动争取时间.

目前， 子母弹毁伤是打击机场跑道的主要有效形式， 因此， 国内外开展了大量子母弹针对机场目标的毁伤研究： 张莉英等[1]在侵彻子母弹抛撒半径选择的基础上， 研究了瞄准点的选择， 进行了机场跑道封锁毁伤的仿真分析. 黄寒砚等[2]采用Monte-Carlo的方法， 模拟子弹落点的生成， 计算了封锁概率和封锁时间. 王刚等[3]采用蒙特卡洛方法对远程制导火箭弹打击机场目标的命中规律进行了求解计算， 通过建立飞机最小升降窗口计算模型， 分析了弹体技术指标对机场跑道毁伤的影响规律. 谭守林、 张建生等[4-5]对子母弹的抛洒半径与机场跑道毁伤概率的关系进行了研究. 黄龙华、 梁敏等[6-7]分别以飞机从跑道强行起降和起降道面所需的时间为研究对象， 分析了封锁型子母弹对机场跑道的毁伤效能. 雷宁利等[8]利用Monte-Carlo方法针对某型侵彻子母弹进行了机场跑道的封锁概率计算. 寇宝华、 刘恒军等[9-10]对末修子母弹对机场跑道的封锁效能进行了评估. 王世强等[11]运用蒙特卡洛方法模拟计算分析了导弹对航空母舰的毁伤效果. 李增华、 王小梅等[12-13]以最小升降窗口为研究对象， 提出了一种窗口扫描算法， 为后续对机场跑道毁伤的深入研究提供了新途径. 吴国东等[14]构建了子母弹抛撒模型， 抽象出了开舱高度， 对不同抛撒高度和抛撒速度下的封锁效能进行了研究. 刘阔[15]建立了子弹抛撒外弹道模型和子母弹对机场跑道的毁伤效能计算模型， 开发了子母弹对机场跑道毁伤效能评估的系统.

上述研究成果多适用于导弹战斗部或机载布撒器类子母弹， 往往只单一考虑毁伤或封锁效能， 而将毁伤与封锁作用耦合考虑的研究尚未有公开文献发表. 对于子母形式的火箭弹， 受限于发射平台， 研发时优先考虑单枚母弹抛撒出的子弹对跑道毁伤封锁的效果， 再根据战术需求制定发射母弹方案. 然而影响单枚母弹毁伤封锁效果的因素中， 除了精度外， 最重要的两个指标就是子弹的数量和质量， 其中， 子弹数量决定了封锁效果， 子弹质量决定了毁伤效果. 由于在母弹的有限空间内， 两个指标成反比关系， 因此如何权衡两个指标的比例关系， 成为同时实现对机场跑道毁伤和封锁效能的关键科学问题.

鉴于上述分析， 本研究运用蒙特卡洛方法形成最小升降窗口区域搜索算法， 构建机场跑道毁伤封锁模型， 制定模拟方案， 分析远程火箭子母弹中子弹数量与质量对机场跑道的毁伤与封锁耦合效能的影响规律.

1 机场跑道的毁伤封锁模型

采用封锁概率作为机场跑道毁伤封锁效能的量化指标， 其中， 影响封锁概率的主要因素有： 机场跑道特性、 子弹的抛撒半径、 子弹的弹坑直径、 子弹的数量、 母弹的打击精度(圆概率误差)等， 根据圆概率偏差和正态分布规律生成母弹、 子弹落点.

1.1 目标特性分析

根据国外飞机跑道承载能力特性以及飞机升降距离， 将跑道简化为长3 000 m， 宽60 m的矩形目标. 飞机跑道参数及典型飞机升降参数分别如表 1， 表 2 所示. 依据表中参数， 制定最小升降窗口为长Lm=300 m， 宽Hm=20 m的矩形区域.

表 1 国外飞机跑道的承载能力Tab.1 Carrying capacity of foreign runway

表 2 飞机升降距离Tab.2 Aircraft lift distance m

1.2 落点随机变量

设母弹瞄准点坐标为A(Xa,Ya)， 命中坐标为B(Xb,Yb)， 设母弹圆概率偏差CEP为RCEP， 考虑母弹命中点坐标服从(μ,σ)的正态分布， 命中点坐标是相互独立的两个满足正态分布的随机变量， 建立如下方程：

(1)

式中：f(x,y)为命中坐标概率分布的密度函数.根据圆概率偏差CEP的定义， 母弹落入半径为RCEP的圆内的概率为0.5， 则

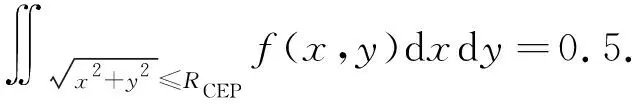
(2)

根据式(1)，式(2)可求得方差σ为

(3)

利用μ和σ产生一个正态分布随机序列

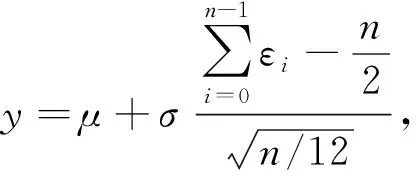
(4)

式中：εi为0～1之间均匀分布的随机数， 当n足够大时(n=12)， 随机数列有较好的正态分布特性， 则式(4)转化为

(5)

由式(5)可获得随机命中落点的坐标序列.

1.3 子弹落点模型

1.3.1 瞄准点位置

为了准确描述瞄准点分布的情况， 构建了跑道直角坐标系， 原点位于跑道轴对称中心， 设定跑道目标为均匀的线目标， 长为2L， 本例中为2 m×1 500 m， 坐标系的原点在跑道中心o处， 各枚火箭母弹的瞄准点以目标中心点为对称等间隔分布.

当发射母弹数量为M时， 第i发母弹的瞄准点为

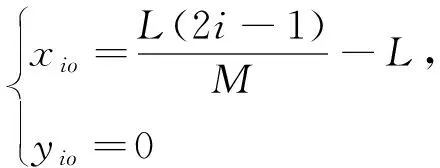
(6)

1.3.2 母弹落点

以圆概率偏差RCEP来表征地面精度， 母弹精度同时受制导性误差和非制导性误差影响[3]. 将母弹落点设定为随机变量， 取火箭弹的瞄准点作为散布中心， 取火箭母弹的落点精度作为散布密集度， 则母弹落点服从圆正态分布. 取圆概率偏差RCEP与射击精度σ的关系为RCEP=1.177 4σ， 设u,v为两个独立的服从(0，1)正态分布的随机数， 则

(7)

式中：RCEPi为第i枚母弹的落点精度.以瞄准点为期望， 以σ=0.849 3RCEPi为方差， 成正态分布随机生成弹落点.

1.3.3 子弹落点

火箭子弹落点散布精度受母弹抛撒方式以及开舱区域气流状况等因素影响， 可以通过加入修正因子， 对火箭子弹落点的偏差进行修正， 如式(8) 所示. 为了简化模型， 设定火箭子弹在母弹抛撒半径内呈均匀分布.

(8)

式中：RCEPj为第j枚火箭子弹圆概率偏差；r为火箭母弹抛撒半径；v1,v2为在(0， 1)区域内生成的均匀随机数.将第i枚母弹中第j枚子弹的落点表示为

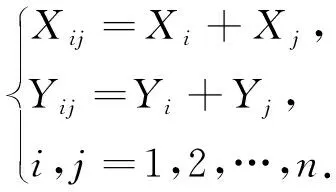
(9)

1.3.4 最小升降窗口区域扫描方法

将落入跑道内部的有效子弹落点(X(k),Y(k))， 按照Y(k)升序排列.如图 1 所示，di为落在跑道上的相邻两枚子弹的纵向距离，ds和dx分别是跑道上距离上边界和下边界最近的两枚子弹与边界之间的距离.R为子弹毁伤半径，H为跑道宽度.对所有相邻子弹距离进行搜索， 若ds-R≥Hm或dx-R≥Hm或di-2R≥Hm中任意一条满足， 则封锁失败， 停止搜索. 否则， 若在跑道上找不到满足飞机起降的最小升降窗口， 则成功建立一条封锁线.

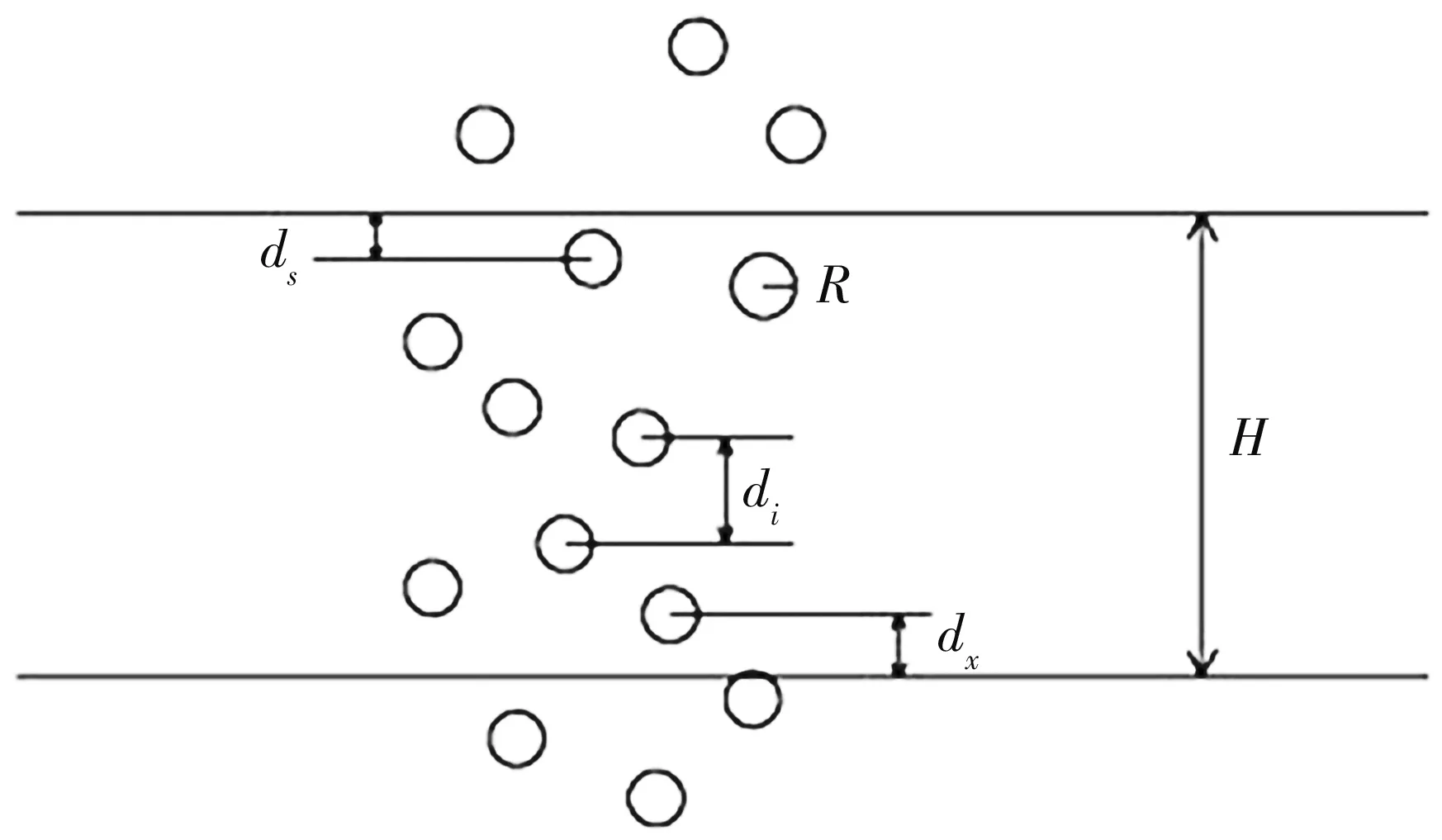
图 1 跑道封锁示意图

2 计算流程及结果分析

2.1 计算流程

根据上述建立的仿真分析模型， 利用蒙特卡洛原理， 模拟母弹、 子弹的随机落点， 对最小升降窗口进行区域搜索， 若搜索不到最小升降窗口则视为封锁成功， 反之失败. 反复模拟A次， 统计成功的数量T， 记封锁概率为P， 则P=T/A×100%. 编制计算流程如图 2 所示.

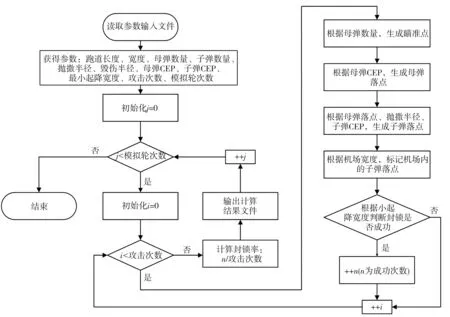
图 2 计算流程Fig.2 Computation flow

2.2 模拟方案及初始参数

对于侵爆类型的火箭子母弹， 如果仅在机场跑道道面形成敞坑或者隐坑毁伤， 敌方易于快速修复， 不利于对跑道的长时间封锁， 因此， 必须对跑道形成隆起毁伤效果， 而当装药量低于 3 kg 时， 隆起毁伤效果较难实现， 因此， 设定装药量大于3 kg.

其他参数设定为： 跑道长度1 500 m； 跑道宽度60 m； 单次攻击投放母弹数量1枚； 母弹抛撒半径100 m； 母弹CEP30 m； 子弹CEP10 m； 最小起降宽度20 m； 每轮模拟的攻击次数为20 000； 按照不同的子弹数量与质量方案分别模拟7轮； 子弹毁伤半径参照表 3.

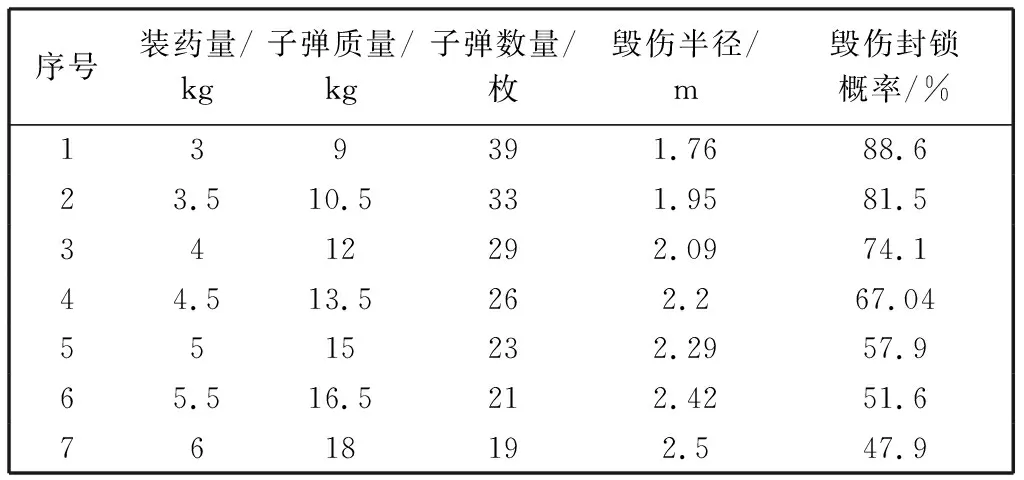
表 3 毁伤封锁概率与各影响因素关系Tab.3 Relationship between damage blockade probability and influence factors

2.3 计算结果及分析

计算得到的封锁概率与子弹质量、 子弹数量、 毁伤半径的关系如表 3 及图 3 和图 4 所示.

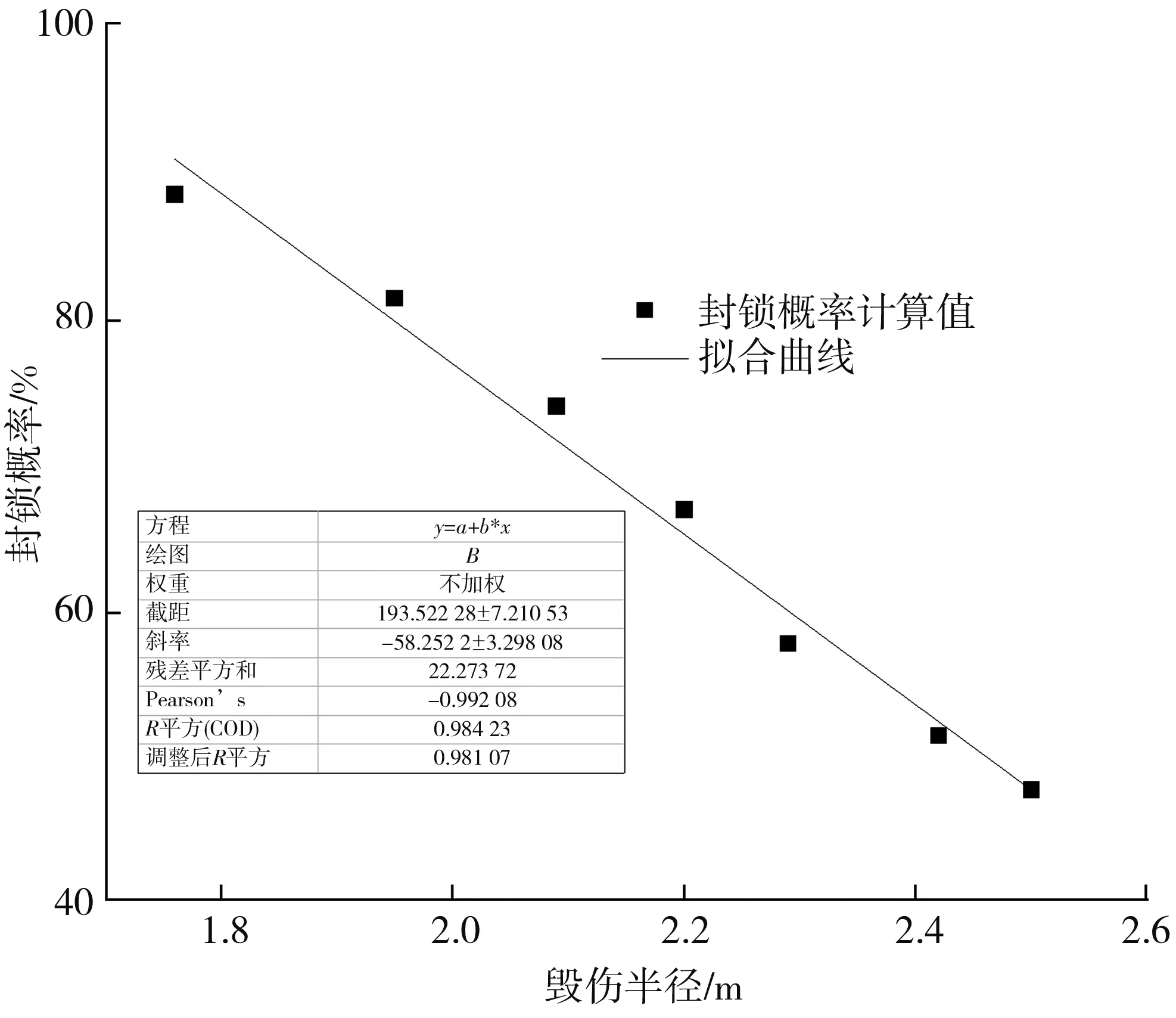
图 3 封锁概率与毁伤半径的拟合函数Fig.3 Fitting function of blockade probability and damage radius

图 4 子弹数量与毁伤封锁概率关系

可以看出， 当装药量≤4 kg， 子弹数量≥30枚时， 毁伤封锁概率大于75%. 子弹质量与封锁概率成线性反比关系. 随着子弹数量增加， 火箭子母弹对机场跑道的封锁概率始终增大. 结合前述分析， 装药量低于3 kg时， 无法形成隆起毁伤， 因此， 综合考虑毁伤封锁效能， 装药量应控制在3 kg～4 kg范围内， 对应的子弹数量为29枚～39枚.

还可以看出子弹数量对毁伤封锁概率的影响高于子弹质量， 因此， 在不大幅降低毁伤半径的前提下， 优先提升子弹数量. 经拟合， 封锁概率与毁伤半径近似满足如下函数关系：

P=193.5-58.3R.

(10)

3 火箭子弹数量设计方法

基于上述毁伤封锁概率与各影响因素的关系， 可提出火箭子弹数量设计总体方案： 首先根据母弹载重确定子弹总重量； 再根据毁伤半径计算出所需子弹质量的第一次取值范围， 进而得到子弹数量的第一次取值范围； 最后拟合出毁伤封锁概率与子弹质量的函数关系， 根据毁伤封锁概率指标计算出子弹质量的第二次取值范围， 进而得到子弹数量的第二次取值范围； 两次取值范围相耦合获得最终子弹数量方案.

火箭子母弹的子弹质量的选取， 应当首先满足单枚子弹对目标的预期毁伤威力. 其次， 根据母弹结构参数及其他技术要求进行质量分配协调， 使分配后对应的子弹数量能够达到预定的毁伤概率.

假定母弹有效载重为500 kg， 其中集束战斗部分离系统结构的质量占总质量的百分比为30%～40%[16]， 本文取值30%， 则子弹总重量为350 kg. 当母弹载重确定时， 子弹的数量与质量满足反比关系， 确定子弹质量方案后， 子弹数量也可同步计算出来.

依据表 3 所示的模拟数据， 拟合毁伤封锁概率P、 子弹毁伤半径R、 子弹质量Gm、 子弹数量N之间的函数关系如下：

子弹毁伤半径R与子弹质量Gm之间的函数关系为

Rmax=1.38ln(3.27ln(Gm/3)，

(11)

式中： 9≤Gm≤18, kg.

子弹质量Gm与子弹数量N之间的函数关系由母弹结构参数给出.

N=500×0.7/Gm.

(12)

联立式(11)和式(12)可得R与N的函数关系为

Rmax=1.38ln(3.27ln(117/N)).

(13)

将式(10)代入式(13)可得封锁概率P和子弹质量Gm的函数关系， 如图 5 和式(14)所示.

P=193.5-80.5ln(3.27ln(Gm/3)).

(14)

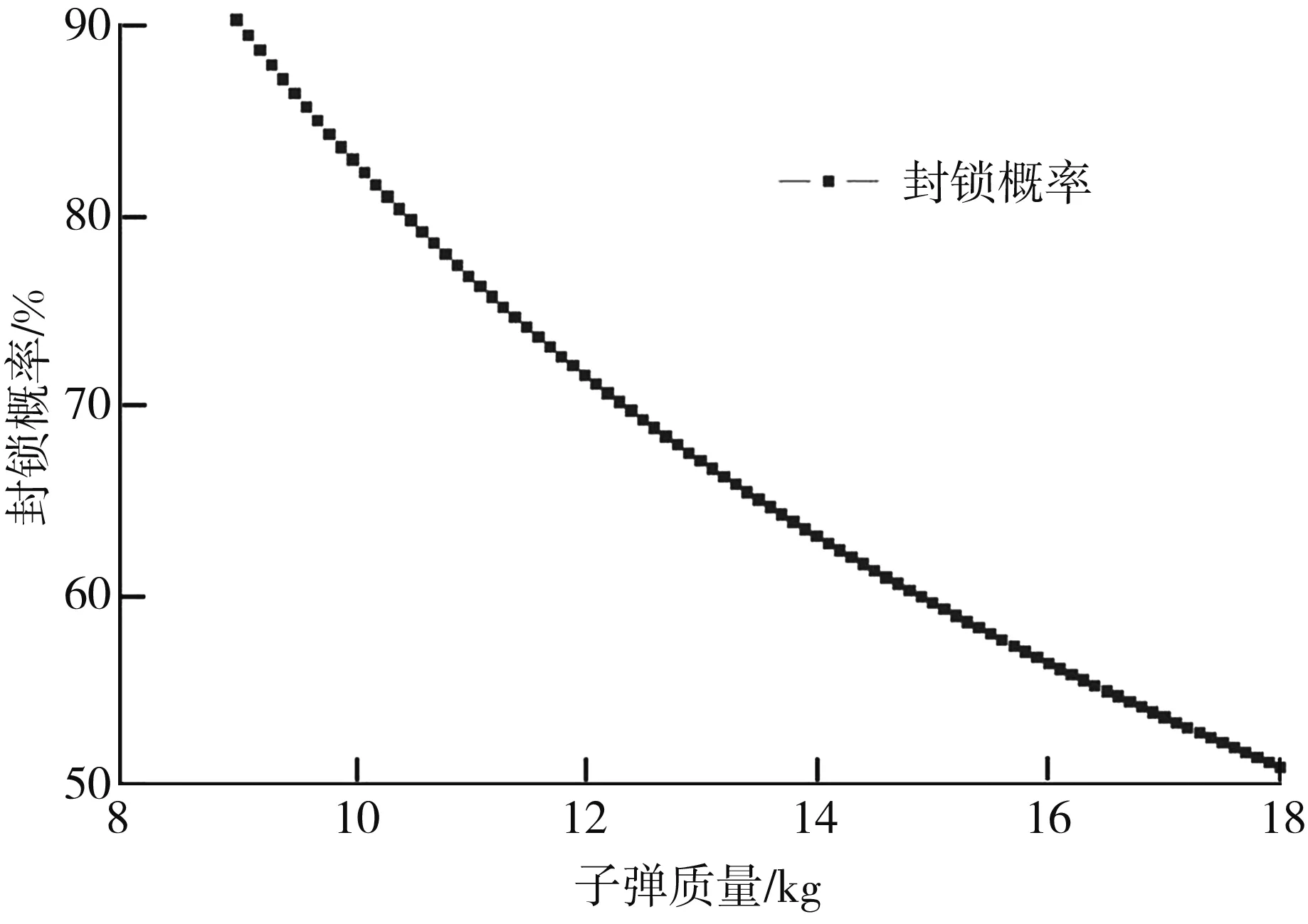
图 5 封锁概率与子弹质量的函数关系Fig.5 Function relationship between blockade probability and submunition mass

4 结 论

采用封锁概率作为机场跑道毁伤封锁效能的量化指标， 构建了火箭子母弹对跑道目标的毁伤-封锁计算模型， 采用蒙特卡洛法分析了火箭子母弹的数量与质量对跑道目标毁伤效能的影响程度. 主要得到以下结论：

1) 当装药量≤4 kg， 子弹数量≥30枚时， 毁伤封锁概率大于75%. 子弹质量与封锁概率成线性反比关系.

2) 随着子弹数量的增加， 火箭子母弹对机场跑道的封锁概率始终增大.

3) 子弹数量对毁伤封锁概率的影响高于子弹质量， 因此， 在不大幅降低毁伤半径的前提下， 优先提升子弹数量.

4) 提出了火箭子弹数量设计计算方法.

5) 为保证有效的毁伤封锁概率， 装药量应控制在3 kg～4 kg范围内， 对应的子弹数量控制在 29枚～39枚.

综上， 本文研究结果可以为火箭子母弹的优化设计及反机场跑道战术布置提供参考.