含湿相变粗糙多孔材质的热质耦合分形研究*
2022-06-15高伟业胡世旺汪振毅
高伟业,张 赛,张 杰,胡世旺,汪振毅
(昆明理工大学 机电工程学院,昆明 650500)
引言
多孔材质内部复杂的传热传质过程对于能源开发和工程隔热等领域至关重要[1-2],因此研究多孔材质的热质耦合传递具有重要的工程应用价值.冯守玲等[3]假定多孔材质为均匀连续结构,构建了不同粒径和不同流速下的多孔介质固定床模型,根据连续性方程对温度场分布进行了数值模拟研究.何增等[4]运用数值离散方法,对气体在低含水率介质中的迁徙进行了数值模拟,得出了估算气体迁徙距离的半经验公式.石金诚等[5]运用能量分析的方法和微分不等式技术,构建了双扩散扰动模型,分析了流体在多孔介质中的流动情况.实际上,多孔材质的内部是非均匀连续的,其内部的结构参数对传热传质过程有着重要意义.徐鹏等[6]和Li 等[7]根据多尺度多孔介质的分形标度特征,建立了光滑单相毛细管道模型,分析了多孔材质内部参数对气体的渗流和扩散机制的影响.张赛等[8]运用分形理论建立了具有随机性的气体扩散模型,分析了气体的不同扩散机制与结构参数之间的关系.陈家豪等[9]根据改进的伪势格子Boltzmann(LB)两相模型,结合几何润湿边界条件,分析了多孔介质内接触角滞后性对非混相驱替效率的影响.Wu 等[10]建立了多尺度的球状模型,将孔隙通道描述为不规则半径毛细管道,推导出不规则半径毛细管道内的渗流系数和导热系数.这些研究只分析了多孔材质的孔道表面为光滑条件下的传热和传质特性.实际工程中,孔道表面一般为粗糙表面,并且多孔材质中的传热传质过程有耦合作用.郑川等[11]基于多孔介质传热和地下水流动理论,建立了一维渗流-传热模型,分析了渗流速度、方向对管道传热特性的影响.张春平[12]建立了粗糙表面管道模型,对粗糙微细通道内的流动和换热特性进行了研究,发现孔道尺度越小,粗糙表面对流动和换热特性的影响越大.盛汉乾[13]建立了微波加热多孔沥青路面耦合模型,分析了含湿状态下孔隙率等结构参数对微波加热效果的影响.可以看出,多孔材质的内部结构、含湿状态和相变都对热质耦合传递过程有着重要影响.
为了准确体现内部结构、含湿状态和相变对热质耦合传递过程的影响,本文运用分形理论构建了含湿相变粗糙表面孔道模型,推导出了含有明确物理参数的渗流系数和耦合等效导热系数的表达式,分析了多孔材质的结构参数、含湿饱和度和相变对热质耦合传递的影响.
1 多孔材质的分形特征


2 含湿相变粗糙表面孔道模型
2.1 Gauss 函数粗糙表面模拟
对于多孔材质孔道粗糙表面的粗糙度的定义大致分为两类:一类为粗糙元的高度与其底部等效半径的比值,称为绝对粗糙度;另一类为粗糙元的高度与孔道半径的比值,称为相对粗糙度.因为相对粗糙度与孔道之间的联系更加明显,本文选取相对粗糙度对孔道粗糙表面进行描述:

式中,ɛ为相对粗糙度;h为粗糙元的高度,m.
在直角坐标系下,假设m个点Pi(xi,yi,zi),其中i的取值区间为[1,m],x和y方向为固定间距取值,z方向为粗糙元的随机高度,xi,yi,zi的表达式为

式中,Δx=0.1,Δy=0.1 分别为x和y方向的增量,ɛ为满足要求的Gauss 函数随机生成的相对粗糙度.
粗糙表面的粗糙元为随机分布并且相对粗糙度ɛ的取值区间一般为0.05~0.1,为了保证99.7%相对粗糙度ɛ的取值分布在此区间,取Gauss 函数置信区间为

可求出函数均值u=0.075,函数标准差n=0.008.
故可构建出符合相对粗糙度ɛ取值区间的Gauss 函数为

式中,函数方差σ=n2.
图1 为孔道粗糙表面的三维仿真图,其中孔道半径r=20 µm,并展开x和y方向长度为20 µm 的粗糙平面.将其划分为200 个网格点,并进行矩阵排列,每一个(xi,yi)点对应一个随机高度zi=ɛr.可以看出粗糙元的高度分布符合随机分布并且符合上述相对粗糙度ɛ的取值区间.

图1 Gauss 函数三维粗糙表面模型Fig.1 The Gauss function 3D rough surface model
2.2 孔道有效半径
根据上述可知,粗糙元的存在对多孔材质孔道半径的影响不可忽略.此外,当孔道内存在湿相并且发生相变时,孔道半径会随着饱和度s的变化而变化,进而影响其内部的热质耦合传递过程,使其耦合传递过程更加复杂.所以当粗糙表面孔道存在含湿相变问题时,其非湿相孔道有效半径可以表示为与相对粗糙度ɛ和饱和度s有关的函数:

从式(13)可以看出相对粗糙度ɛ和饱和度s都是其重要的影响因素.
3 含湿相变粗糙表面多孔材质渗流系数
3.1 渗流量

3.2 渗流系数

4 含湿相变粗糙表面多孔材质耦合等效导热系数
含湿相变粗糙表面多孔材质内部的传热过程十分复杂.其内部包括固相、湿相、气相各自和彼此之间的传热过程,此外渗流过程也会极大地影响传热过程.下文分析了各相的传热过程以及热质耦合传递过程,并推导出热质耦合作用下的等效导热系数.
4.1 固相传热过程
固相的传热过程主要包括固相之间的热量传递、固相的热量储存以及固相和湿相之间的热量传递:

式中,(ρc)m为固相密度比热容积,kJ/( kg·m3·K);∂Tm/∂t为固相温度变化梯度,℃/s;∂Tm/∂l为固相两端温度梯度,℃/m;Q1为固相与湿相之间的对流换热量,kJ;λm为固相在Tm下的导热系数,W/(m·K).
4.2 湿相传热过程
湿相的传热过程主要包括湿相传质过程引起的热量传递,湿相的热量储存,湿相和固相、气相之间的热量传递以及湿相相变引起的热量传递:

式中,(ρc)w为湿相密度比热容积,kJ/( kg·m3·K);∂Tw/∂t为湿相温度变化梯度,℃/s;∂Tw/∂l为湿相两端温度梯度,℃/m;Q2为湿相与固相、气相之间的对流换热量,kJ;γ 为湿相相变潜热系数;λw为固相在Tw下的导热系数,W/(m·K);uw=kcwΔP/(µwL0)为湿相的渗流速度,m/s;M=(s1–s)ρv为湿相的相变质量,kg.
4.3 气相传热过程
气相的传热过程主要包括气相传质过程引起的热量传递、气相的热量储存以及气相和湿相之间的热量传递:

式中,(ρc)g为湿相密度比热容积,kJ/( kg·m3·K);∂Tg/∂t为气相温度变化梯度,℃/s;∂Tg/∂l为气相两端温度梯度,℃/m;Q3为气相与湿相之间的对流换热量,kJ;λg为气相在Tg下的导热系数,W/(m·K);ug=kcgΔP/(µgL0)为气相的渗流速度,m/s.
根据能量守恒有

4.4 热质耦合等效导热系数
联立式(21)~(24),根据Fourier 热传导定律,在考虑相对粗糙度、饱和度以及耦合作用情况下的热质耦合等效导热系数的表达式为

式中,λdeff为等效导热系数,W/(m·K);∂Tdeff/∂l为等效温度梯度,℃/m.可以看出,对于多孔材质而言,其内部结构参数、传质过程和相变对传热过程有着重要的影响.
5 分析与讨论
上文已给出多孔材质孔道相对粗糙度的取值区间为0.05~0.1.分形维数可由分形理论与孔道半径求得,当rmin/rmax→ 10–3,孔隙率取值在0.25~0.5 时,面积分形维数Df取值为1.8~1.9,迂曲分形维数Dt取值为1.1~1.2.
5.1 等效导热系数与孔隙率的关系
图2 为多孔材质等效导热系数λdeff的数值解与理论解的对比.从图2 中可以看出,当不考虑耦合和相变因素时,式(25)得到的数值解与文献[15]中的理论解吻合得很好.当考虑耦合和相变因素时,等效导热系数λdeff会有所增大,并且增大幅度随着孔隙率φ 的增加而增大.这是因为孔隙率φ 的增加会增大湿相的含量,从而导致渗流量和相变量增加,并且渗流和相变引起的热量传递远大于固相和气相引起的热量传递.通过以上分析可知,渗流和相变引起的热量传递在等效导热系数中的占比较大.
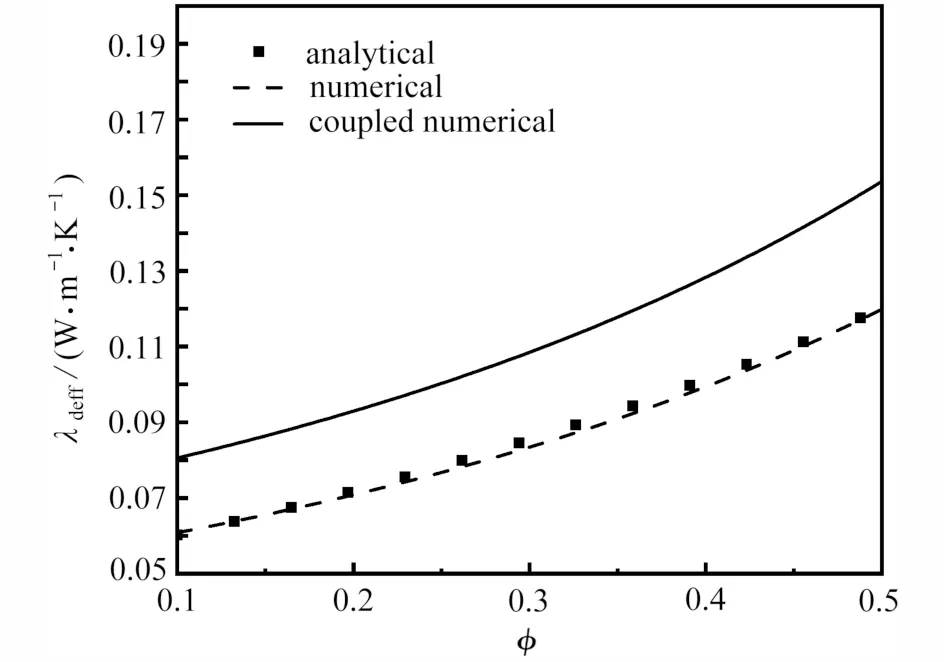
图2 等效导热系数λdeff 与孔隙率φ 的关系Fig.2 The relationship between equivalent thermal conductivity λdeff and porosity φ
5.2 环状渗流系数的影响因素
图3 为在不同的面积分形维数Df下湿相环状渗流系数kcw与饱和度s的关系.图3 表明,当相对粗糙度ε=0.075,迂曲分形维数Dt=1.15,面积分形维数Df分别为1.8,1.85,1.9 时,kcw随着s的增大而增大,并且kcw的变化幅度逐渐减小,在s=0.7 后,kcw趋近于湿相饱和渗流系数.这是因为s增大,湿相含量增加,渗流量增加,并且随着s的增大,湿相含量的增加量越来越少.同时,图3 也表明,当s相同时,Df越大,kcw越大.这是因为Df越大,孔隙率越大,并且大孔径孔道的数量增加,流动性能提高,有利于渗流.
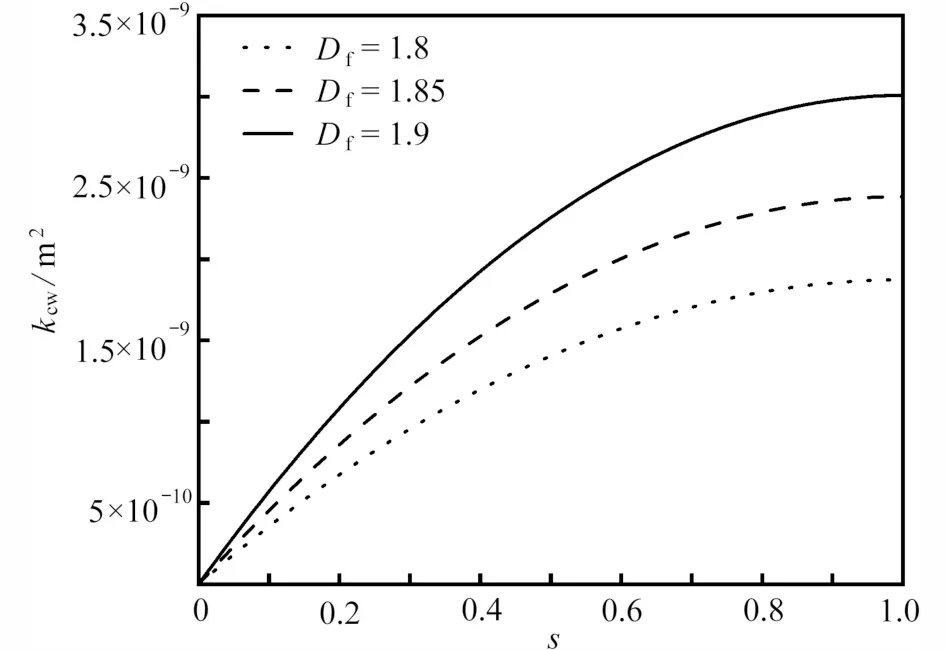
图3 面积分形维数Df 对环状渗流系数kcw 的影响Fig.3 The influence of area fractal dimension Df on annular seepage coefficient kcw
图4 给出了在不同的迂曲分形维数Dt下湿相环状渗流系数kcw与饱和度s的关系.图4 表明,当ε=0.075,Df=1.85,Dt分别为1.1,1.15,1.2 时,kcw随着s的增大而增大.图4 也表明,当s相同时,Dt越大,kcw越小.这是因为Dt越大,孔道的迂曲程度越大,渗流过程中阻力越大,越不利于渗流.
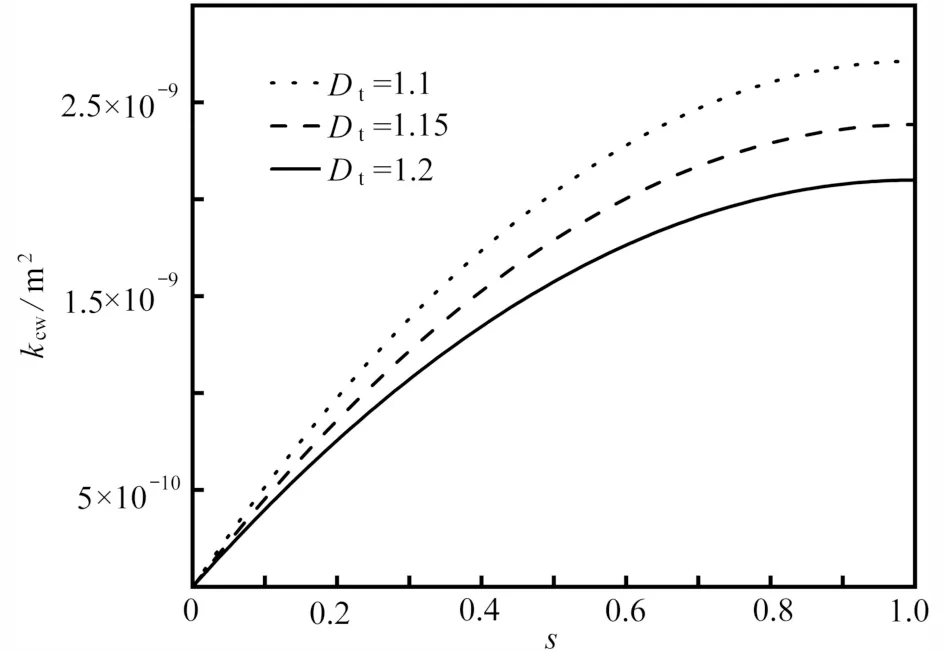
图4 迂曲分形维数Dt 对环状渗流系数kcw 的影响Fig.4 The influence of tortuous fractal dimension Dt on annular seepage coefficient kcw
图5 给出了在不同的饱和度s下湿相环状渗流系数kcw与相对粗糙度ε 的关系.图5 表明,当Df=1.85,Dt=1.15,s分别为0.4,0.5,0.6 时,kcw随着ε 的增大而减小,并且随着ε 的增大,不同s取值下的kcw差距逐渐减小.这是因为相对粗糙度ε 越大,孔道有效半径越小,渗流量减少,kcw减小,并且ε 越大,影响作用越明显.同时,图5 也表明,当ε 相同时,s越大,kcw越大.这是因为s越大,湿相含量越大,渗流量越大,kcw越大.
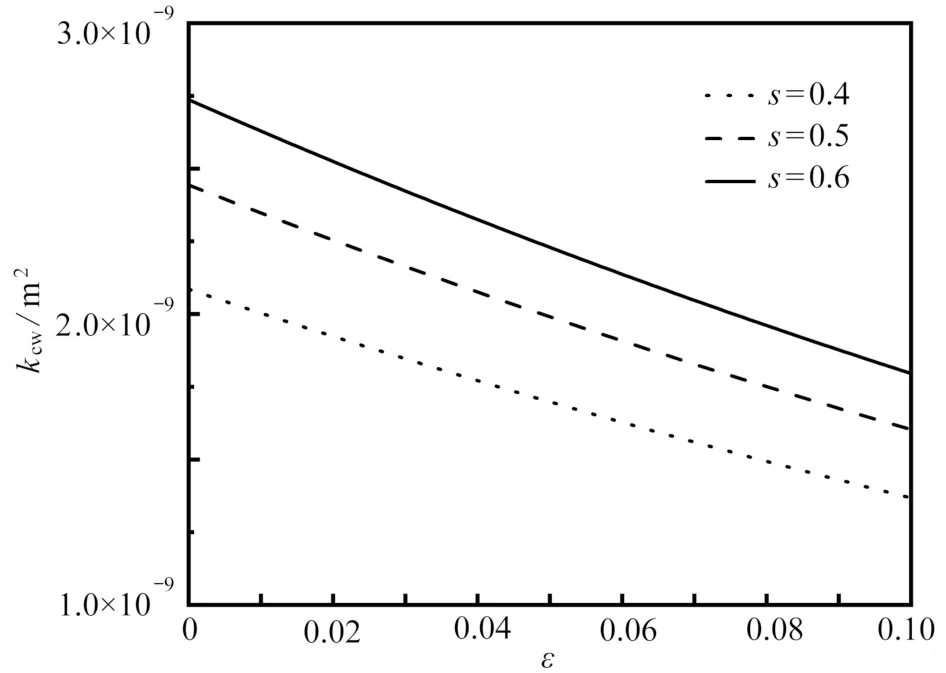
图5 饱和度s 对环状渗流系数kcw 的影响Fig.5 The influence of saturation s on annular seepage coefficient kcw
5.3 等效导热系数的影响因素
图6 给出了在不同渗流系数下等效导热系数λdeff与相对粗糙度ε 的关系.图6 表明,当渗流系数相同时,λdeff随着ε 的增大而减小.这是因为随着相对粗糙度ε 的增大,孔道的有效半径减小,孔隙率φ 减小,虽然固相的热量传递有所增加,但增加量远小于湿相和相变的热量传递减少量,与图2 分析一致.同时,图6 也表明,当ε 相同时,λdeff随着渗流系数的增加而增大.这是因为渗流系数增加,湿相和气相的渗流速度增加,渗流量增加,渗流过程对热量传递的影响增大.
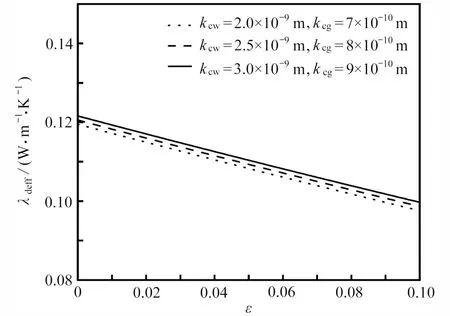
图6 渗流系数对等效导热系数λdeff 的影响Fig.6 The effect of the seepage coefficient on equivalent thermal conductivity λdeff
图7 给出了在相同初始饱和度s1=0.5 时,不同饱和度s下的等效导热系数λdeff与相对粗糙度ε 的关系.图7表明,当ε 相同时,λdeff随着s的减小而增大.这是因为饱和度s减小,相变量增加,相变的热量传递增加量大于渗流的热量传递减少量.同时,图7 也表明,当ε 越来越大,不同s下的λdeff差距越来越小.一方面是因为相变对热量传递的影响越来越小;另一方面是因为有效半径减小,孔隙率φ 减小,相变引起的气体膨胀压强差对渗流速度的促进效果越来越明显,同一ε 下,渗流量增加,渗流对热量传递的影响增大.

图7 饱和度s 对等效导热系数λdeff 的影响Fig.7 The influence of saturation s on equivalent thermal conductivity λdeff
6 结论
本文根据Gauss 随机分布函数建立了含湿粗糙表面孔道模型,运用分形理论推导出了含湿相变粗糙表面多孔材质的渗流系数和耦合等效导热系数的表达式.定量分析了面积分形维数、迂曲分形维数、含湿饱和度及相对粗糙度对渗流系数、耦合等效导热系数的影响.结果表明:
1)湿相非饱和渗流过程中,环状渗流系数随着饱和度的增加而增大,并且增大幅度逐渐减小.当饱和度到达0.7 后,环状渗流系数趋近于饱和渗流系数.
2)热量传递过程中,渗流和相变引起的热量传递对等效导热系数的影响不可忽略.
3)相同初始饱和度的情况下,孔隙率越小,相变对热量传递的效果越来越不明显,相变引起的气体膨胀压强差越来越明显.
