含间隙非线性弹性超材料的低频宽带机理*

林 臻，吴九汇

（西安交通大学 机械工程学院，西安 710049）

引言

目前，利用线性隔离系统[1-5]通常可以有效降低振动噪声中的线谱成分，但不能改变谱线特性，难以隔离低频线谱，对低频线谱的隔离仍然是一个挑战.基于线性隔振技术的局限性，非线性振动隔离技术激起了国内外学者的极大关注，因为它可以实现较低的动态刚度并降低固有频率，故非线性振动隔离在噪声控制领域内应用非常广泛[6-12]，如准零刚度[13-15]用于振动隔离以及复杂非线性动力学.更重要的是，非线性振动隔离机理与线性隔振技术相比具有许多优点：一方面，非线性混沌隔振系统可以较好地改变噪声中的频谱结构，进而有效隔离低频线谱；另一方面，带隙的宽度由于非线性机制而扩大，因为当系统运动进入混沌状态时，线性谱能量大大削弱，从而变成了一个连续的宽频谱.尽管非线性混沌隔振机理可以实现低频宽带隙[16-18]，然而，绝大多数非线性研究只关注物理参数高阶项的非线性干扰或一些较弱的几何非线性[19-22]，对非线性结构系统产生的较强的非线性机理及现象研究甚少，尤其基于非线性弹性碰撞振动系统的结构非线性来调控弹性波带隙的机理及相关研究仍甚少.

本文基于非线性隔振机理的优点，将含间隙非线性机理引入到局域共振结构中，提出了一种具有较小间隙的非线性新型局域共振结构设计的新理念，系统地分析了非线性弹性碰撞局域共振结构带隙的产生机理.最后，通过有限元法研究了该非线性局域共振弹性超材料板的弹性波振动带隙特性及其透射谱的减振降噪特性.

1 非线性碰撞振动系统的动力学特性

1.1 含间隙非线性碰撞振动系统的理论模型

首先，本节提出了如图1所示的非线性弹性碰撞系统的弹簧质量系统.在该非线性模型中，基体m1和局域共振质量块m2通过弹簧系数为k1，k2和k3的弹簧连接，并且弹簧k3与局域共振振子m2之间有一个小间隙，而不是直接与该振子相连接.

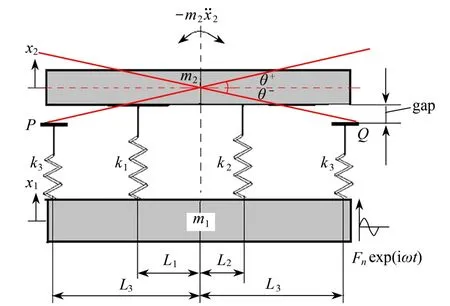
图1 非线性碰撞振动系统Fig.1 The nonlinear collision vibration system

在基体m1施加x方向上的激振力.那么，局域共振振子m2包含三种运动状态：① 局域共振振子m2只在x方向上移动，与弹簧k3无任何接触；② 局域共振振子m2围绕其质心转动，与点Q处的弹簧k3接触并碰撞；③ 局域共振振子m2的速度方向改变，局域共振振子m2再次与点P处的弹簧k3接触并碰撞，并且这三类运动周期性地重复.因此，这是一个典型的分段非线性碰撞振动系统.根据Newton 第二定理：

1）当θ≥θ+时，该非线性振动系统的运动方程为

2）当θ−<θ<θ+时，该非线性振动系统的运动方程为

3）当θ≤θ−时，该非线性振动系统的运动方程为

上述公式中m1=0.023 kg，m2=0.195 kg，k1=k2=1625,k3=1 950，L1=L2=0.000 6 m，L3=0.001 8 m.在这个典型的分段非线性系统中，随着间隙的变化，该系统将从周期运动历经倍化分岔最终进入混沌状态.下面分析该非线性振动系统的非线性动力学特性.

1.2 含间隙非线性碰撞振动系统的动力学特性

图2 描述了振子m2的相图及基体m1的位移响应频谱图.从图2 可以很清楚地看出，随着间隙的变化，该系统由稳定的1-1-1 周期运动发生倍化分岔，当间隙为0.065 mm 时，系统进入1-2-2 周期运动，基体m1的位移频谱幅值为0.12 mm，如图2(b)所示.随着间隙的进一步减小，系统又进入2-4-4 周期运动，这时该振子m2与点P和点Q处的弹簧k3各碰撞两次，如图2(c)所示.同时在基体m1位移响应频谱图上，产生两条线谱，且幅值均为减小趋势，如图2(d)所示.当间隙为0.05 mm 时，该系统又发生倍化分岔，分岔出两条通道，进而系统进入4-8-8 周期运动，如图2(e)所示.在基体m1位移响应频谱图上，产生四条线谱，第一条线谱幅值由0.12 mm 减小到0.075 mm，而其他三条的幅值均小于0.03 mm，如图2(f)所示.这也意味着该系统由周期运动历经倍化分岔，能量越来越小.随着控制参数间隙的继续减小，该系统最终进入混沌状态，如图2(g)所示.最重要的是，基体m1位移响应频谱图成为了连续频谱，大部分频谱线的幅值均小于0.01 mm，如图2(h)所示.

图2 不同间隙下m2 的相图及基体m1 的位移响应频谱图：(a)间隙为0.065 mm，m2 相图；(b)间隙为0.065 mm，m1 频谱图；(c)间隙为0.062 mm，m2 相图；(d)间隙为0.062 mm，m1 频谱图；(e)间隙为0.05 mm，m2 相图；(f)间隙为0.05 mm，m1 频谱图；(g)间隙为0.013 5 mm，m2 相图；(h)间隙为0.013 5 mm，m1 频谱图Fig.2 Phase diagrams of m2 and displacement response spectra of matrix m1 under different gaps:(a)gap is 0.065 mm,the m2 phase diagram;(b)gap is 0.065 mm,the m1 displacement response spectrum;(c)gap is 0.062 mm,the m2 phase diagram;(d)gap is 0.062 mm,the m1 displacement response spectrum;(e)gap is 0.05 mm,the m2 phase diagram;(f)gap is 0.05 mm,the m1 displacement response spectrum;(g)gap is 0.013 5 mm,the m2 phase diagram;(h)gap is 0.013 5 mm,the m1 displacement response spectrum

显然，该系统由周期运动历经倍化分岔进入混沌状态时，线性谱能量大大削弱，变成了一个连续的宽频谱，这意味着不仅线谱成分的特性被大大削弱，而且系统振动被有效地抑制了.因此，混沌特性可以有效减少线谱成分，下面我们将非线性混沌隔振机理引入到局域共振弹性超材料结构中，设计一种新型含间隙非线性局域共振弹性超材料板，并通过有限元方法详细分析了该非线性局域共振结构的带隙及相关性能.

同时，如果间隙较大时，局域共振振子m2并不能与点P或点Q处的弹簧k3接触并发生碰撞，故此时该系统为线性系统.图3 描述了当间隙较大时，该线性系统振子的相图.如图3所示，当间隙大于0.1 mm 时，该系统并没有非线性碰撞运动产生，故其为线性系统.

图3 间隙为0.1 mm 线性系统m2 的相图Fig.3 Gap is 0.1 mm,linear system m2 phase diagram

图4 描述了基体的位移响应频谱图.从图4(a)可以清楚地看到，当间隙较大时，线性系统基体m1的位移响应频谱图上只有一条谱线，且该基体m1的振幅为1.2 mm；图4(b)描述了当该系统为非线性系统，但未进入混沌状态时，基体m1的位移响应频谱图上分岔出多条线谱，且幅值大幅度减小了；图4(c)描述了非线性系统在混沌状态下m1的位移响应频谱图，此时为连续频谱，且最大谱线的幅值较线性系统的幅值减小了约两个数量级.也就是说，从能量的角度来看，系统从周期运动历经倍化分岔进入混沌状态时，能量大幅度衰减且分布在较宽的频带上.

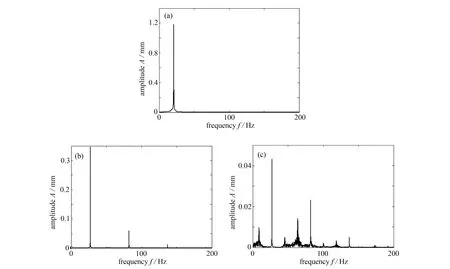
图4 基体m1 的位移响应频谱图：(a)线性系统基体m1 的位移响应频谱图；(b)未混沌状态下非线性系统m1 的位移响应频谱图；(c)混沌状态下非线性系统m1 的位移响应频谱图Fig.4 Displacement response spectrograms of matrix m1:(a)the linear system m1 displacement response spectrum;(b)the displacement response spectrogram of nonlinear system m1 in the unchaotic state;(c)the displacement response spectrogram of nonlinear system m1 in the chaotic state

2 含间隙非线性弹性超材料板的低频带隙形成及调控机理

2.1 含间隙非线性弹性超材料板的结构单元

基于上述非线性振动隔离原理，本文将含间隙非线性机理引入到局域共振结构,提出了如图5所示的含间隙非线性弹性超材料板的结构单元.在该模型中，弹簧系数为k1，k2的弹簧分别由各向同性的有机玻璃方板代替，弹簧系数为k3的弹簧由硅橡胶代替.其中弹簧系数为k3的两个硅橡胶块与局域共振质量块m2之间具有0.5 mm的间隙.并且，在该模型中，构件2 为长和宽1.5 mm、高2.5 mm 的有机玻璃长方体，构件1 为长和宽1.5 mm、高2 mm 的硅橡胶长方体，振子为长和宽15 mm、高3 mm 的铅板，基体为长和宽15 mm、高1.5 mm 的铝方板.

图5 局域共振弹性超材料结构：(a)无间隙局域共振结构单元；(b)含间隙局域共振结构单元Fig.5 The local resonance elastic metamaterial structure:(a)the gapless LR structural unit;(b)the gapped LR structural unit

2.2 含间隙非线性弹性超材料板的带隙计算方法

为了研究这类含间隙非线性弹性超材料板的弹性波带隙，通过有限元方法计算了该结构的带隙.在计算带隙时，根据Bloch-Floquet 定理，取在局域共振相邻连接单元界面上的周期边界条件，并且引入了Bloch波K.通过改变不可约的第一Brillouin 区（BZ，如图6所示）K的值，可以获得色散关系以及本征模态.

图6 第一Brillouin 区Fig.6 The 1st Brillouin zone

取一组参数如表1所示，用商业软件COMSOL 5.5 计算局域共振弹性超材料板的带隙.

表1 材料参数Table 1 Material parameter

对于无间隙的局域共振结构(如图5(a)所示)，图7(a)描述了该结构的带隙，很显然在该结构中产生了7 条带隙，但是由于弹性波衰减较弱，所以各个带隙之间并没有弹性波带隙形成.相反，在该结构中引入0.5 mm的间隙时(如图5(b)所示的非线性局域共振结构)，该局域共振结构便变为一个含间隙的典型非线性系统，图7(b)描述了该含间隙非线性局域共振结构的带隙.我们可以很清楚地看到，在第6 条和第7 条带隙之间产生了一条35～215 Hz 的超低频宽带.因此，说明该弹性波带隙确实是由于这个0.5 mm 的间隙所引起的非线性机理导致的，非线性混沌机理确实可以实现较好的低频隔振效果.

图7 局域共振结构带隙:(a)无间隙局域共振结构的带隙；(b)含间隙非线性局域共振结构的带隙；(c)图(b)中带隙下界对应的放大图Fig.7 Local resonance structure band gaps:(a)band gaps of gapless local resonance structures;(b)band gaps of gapped local resonance structures;(c)the enlarged view corresponding to the lower bound of the band gaps in fig.(b)

2.3 含间隙非线性弹性超材料板的低频宽带特性

为了验证结构的减振特性，计算了通过沿着x轴五个周期的有限结构的透射率，且在y方向上的边界上施加了Bloch 周期条件.谐波位移激励被施加在板表面上的一侧点S，并且该局域共振板的另一侧拾取平均点T的位移响应，如图8所示，透射率定义如下：

图8 间隙非线性弹性超材料板Fig.8 The band gapped nonlinear elastic metamaterial plate

式中，din为板的输入平均位移，dout为板的输出平均位移.

为了进一步证明该含间隙非线性局域共振弹性超材料板的低频弹性波带隙的存在，图9(a)描述了该结构的弯曲振动透射率，在透射谱中有一个具有明显衰减的低频区域（灰色区域），并且它们的位置和图9(b)的带隙之间具有良好的一致性，故该含间隙非线性局域共振弹性超材料板在35～215 Hz 之间具有较好的减振降噪效果.

图9 非线性局域共振结构的带隙及传输率:(a)弹性波的透射率；(b)带隙Fig.9 Band gaps and transmission rates of nonlinear local resonance structures:(a)the transmissivity of elastic waves;(b)band gaps

3 基于非线性混沌理论的低频宽带机理

上述分析结果表明，基于间隙非线性混沌机理，所提出的含间隙非线性超材料板中存在一个明显的弹性波带隙.为了进一步揭示这种现象，图7（c）和图9（b）中标记的模式的本征模态形状和位移矢量场如图10所示.图10 的彩色部分表示位移矢量场的大小，对于模式A，局部共振质量m2与点Q处的硬弹簧k3接触并发生碰撞.对于模式B，局域共振振子沿着x轴方向旋转，而基板保持静止.对于模式C，局域共振振子在z方向上做较大振幅振动.对于模式D，局部谐振质量沿y轴方向沿着不同的轴线旋转，而基板保持不动.在模式E中，局域共振振子m2再次与点P处的弹簧k3接触发生弹性碰撞，由于该非线性碰撞振动系统由周期运动历经倍化分岔进入混沌状态，能量越来越低，能量全部分布在了较宽的频带上，进而导致了35～215 Hz 的低频宽带.很显然，在模式A到E中，局域共振振子分别与点P和Q处的弹簧k3发生碰撞.在模式C中，局部共振质量m2在z方向上振动，与弹簧没有任何接触碰撞，这几个阶段的振动模式与上述理论分析的分段非线性运动趋势高度一致.那么，在分段非线性系统中，旋转碰撞运动（在点P或Q处）和x方向上的移动周期性地重复，同时也呈现非线性运动，即从单周期到倍化分岔，最终进入混沌状态，每一次倍化分岔后的新线谱强度大大降低.因此，如模式E所示，在混沌状态之后，较多的能量最终分散到宽频带上，弹性波带隙被打开.然后，在非线性碰撞之后线谱能量被大大削弱，局部谐振质量和基体由于非常小的振幅而保持静止，如模式F所示，此时弹性波带隙闭合.因此，弹性波带隙确实是由非线性混沌机理引起的，间隙碰撞非线性系统确实具有很强的隔离线谱能力.几何参数对带隙的影响将在第4 节讨论.

图10 非线性局域共振结构各个点的振型:(a)A 点的模态；(b)B 点的模态；(c)C 点的模态；(d)D 点的模态；(e)E 点的模态；(f)F 点的模态Fig.10 Mode shapes at various points of nonlinear LR structures:(a)point A modal;(b)point B modal;(c)point C modal;(d)point D modal;(e)point E modal;(f)point F modal

4 间隙非线性对弹性超材料板带隙的影响

图11 描述了间隙大小对含间隙非线性局域共振弹性超材料板的弹性波带隙的影响.很显然，当间隙小于0.45 mm 时，即间隙较小，非线性机理几乎不存在，该结构无弹性波带隙产生；当间隙大于0.85 mm 时，局域共振振子由于间隙较大不能发生间隙碰撞，即也不能产生非线性现象，导致弹性波衰减较弱，故无弹性波带隙形成；当间隙大于0.45 mm 小于0.85 mm 时，该局域共振结构为典型的分段非线性系统，产生了从周期运动历经倍化分岔进入混沌的非线性运动现象，在混沌状态时，基体的位移响应频谱幅值降到了较低的频率范围内，且形成了较宽的频带，故产生了35～215 Hz 的低频宽带.最重要的是，从分析结果来看，确实是由于间隙非线性机理导致了低频宽带的形成.当然，基于非线性混沌理论，对于其他结构应按照对应尺寸来确定合适的间隙.

图11 间隙对非线性局域共振结构带隙的影响Fig.11 Influences of gaps on the band gaps of nonlinear LR structures

事实上，当间隙较大时，局域共振的振子并不能发生弹性碰撞，故该系统为线性系统；当间隙较小时，系统非线性较弱，近似为线性系统.在这两种情况下并不能产生混沌非线性，导致弹性波不能大幅度衰减，故无弹性波带隙形成，这也与图3 和图4 所描述的情况吻合.因此说明确实是由于间隙引起的混沌非线性机理导致了弹性波带隙的产生，这类含间隙的非线性局域共振弹性超材料板的低频宽带的形成机理在减振降噪应用领域内具有非常重要的理论意义和实际应用价值.

5 结论

在本文中，基于非线性混沌理论，提出了一种含有间隙的新型非线性局域共振弹性超材料板.用有限元方法获得了该新型超材料板的带隙和透射率，研究结果表明，该非线性局域共振新型结构确实是由于间隙碰撞振动引起的非线性现象导致了低频宽带的产生.随后，通过研究带隙边缘处的本征模态的位移场分析了带隙的形成机理.最后，详细分析讨论了几何参数(间隙)对弯曲波带隙的影响.在分析过程中得出了以下结论：

1）在含间隙非线性碰撞振动系统中，该系统产生了混沌，即从单周期历经倍化分岔，最终进入到混沌状态.在这个非线性运动过程中，基于振动元件的每个谐波频率之间的相互作用耦合，在每一次倍化分岔后出现的新线谱强度大大降低.然后，在进入混沌状态之后，所有的频谱幅值都降到了非常低，这意味着所传输的振动能量被分布到了较宽的频带上.

2）基于非线性混沌隔振理论，提出了含有小间隙的非线性局域共振弹性超材料板的设计新理念.当引入0.5 mm 的间隙时，局域共振系统变为典型的非线性碰撞振动系统，正是基于非线性混沌机理，该含间隙的非线性局域共振弹性超材料板产生了35～215 Hz 的弹性波带隙.最重要的是，弹性波带隙形成的振动模式与理论运动趋势高度一致.因此，将间隙引入到局域共振结构中，可以有效降低线性谱，并成功抑制低频弯曲波振动.

3）通过分析间隙对含间隙非线性局域共振弹性超材料板的弹性波的影响，发现间隙较大时不能完全产生碰撞运动，故不能产生较强的非线性现象，进而无法有效降低频谱幅值，导致弹性波衰减程度降低.只有在合理的尺寸范围内，这个小间隙才可以产生较强的非线性碰撞机理，进一步揭示了该非线性局域共振弹性超材料结构带隙的产生确实是由间隙的存在产生.

总之，本文基于非线性混沌隔振机理，所提出的含极小间隙新型非线性弹性超材料能够有效改变频谱特性并隔离弯曲波的低频线谱，为声弹性超材料的发展开辟了新天地，在减振降噪应用研究领域内具有潜在的工程应用价值.