基于黏聚区模型的ENF试件层间裂纹扩展分析*
2022-06-15肖鹏程王增贤邵光冉卢天健
邓 健,肖鹏程,王增贤,邵光冉,卢天健
(1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016;2.南京航空航天大学 多功能轻量化材料与结构工信部重点实验室,南京 210016)
引言
为有效分析裂纹的萌生与扩展过程,黏聚区模型(cohesive zone model,CZM)被广泛应用于纤维增强复合材料层合板结构的分层失效与界面脱黏的模拟[1-2].相对于有限元数值方法,解析法形式简单,且不存在数值稳定性的问题,能够以较低成本讨论界面性能参数、本构形式对裂纹扩展和最终失效载荷的影响,有利于深入研究分层损伤扩展的力学行为.此外,理论研究可为断裂韧性试验的设计和数据处理方法的发展提供理论基础,且对数值仿真结果的有效性验证有一定的补充作用,进而促进CZM 在复杂结构层间损伤分析中的应用[3-4].
端部缺口弯曲(end notched flexure,ENF)试件是评估复合材料层合板Ⅱ型(剪切型)断裂的标准形式,国内外学者针对其裂纹扩展过程的建模、分析和设计展开了广泛研究.例如,Hashemi 等[5]基于修正梁理论研究了ENF试件的裂纹扩展过程;Carlsson 等[6]讨论了横向剪切变形对能量释放率(GⅡ)的影响;Fan 等[7]和Valvo[8]指出基于梁理论的ENF 模型忽略了裂纹尖端的塑性变形;而Whitney 等[9]将裂尖应力奇异性引入ENF试件的剪切梁模型.随后Whitney[10]基于Reissner 变分原理发展了Ⅱ型裂纹扩展的高阶梁模型.此外,Williams[11]在分层裂纹长度中引入与材料弹性参数有关的修正量χ,考虑了裂尖变形和转角的影响.陈瑛和乔丕忠[12]将双线性黏聚区本构引入到4ENF试件中,研究了界面应力分布情况,但并未详细讨论裂纹扩展过程.刘伟先等[13]研究了ENF试件中的裂纹扩展,认为裂纹扩展之后黏聚区长度保持定值,但仅考虑了ENF试件的裂纹长度小于试件半长的情况.
本文基于经典层合板理论及CZM,建立了含一般分层裂纹层合板的理论模型,对纯Ⅱ型断裂ENF试件进行裂纹扩展理论分析.相较于传统的梁理论,该模型充分考虑黏聚区的软化过程,引入了试件发生失效前的非线性行为.将模型预测与试验结果及梁模型预测进行对比,验证了其有效性.基于所提出的模型,研究了典型ENF试件载荷-位移曲线和黏聚区长度对界面参数、裂纹长度的响应,并讨论了裂纹长度超过试件半长时,裂纹扩展对黏聚区长度的影响.本文研究不仅为复杂结构的分层裂纹扩展分析提供了理论依据,还为数值仿真提供一个可靠的交叉检验工具.
1 含一般分层裂纹的层合板模型
本文考虑含有一般分层裂纹的复合材料层合板,层合板长2L、宽b,分层后的上下半板的厚度分别为h1,h2,其几何尺寸及坐标系如图1所示.如图所示,贯穿层合板的宽度方向且与其长度方向平行的分层裂纹长度为a,假设该裂纹仅向层合板内部并沿已有裂纹方向扩展,潜在裂纹在图中以虚线标出.根据黏聚区模型,裂尖区域存在黏聚区,通过界面应力作用于潜在裂纹的上下表面,界面应力分布可由基于相对位移的黏聚区本构关系确定.进一步假设层合板为薄壁结构,符合经典层合板理论的应用范围[14],则上下两半板在各自局部坐标系中的位移场可表示为

裂纹扩展过程中,假设上下两半板处于小变形状态.根据上下两半板微元段的受力平衡条件(图1),忽略高阶项,则含一般分层裂纹的复合材料层合板(上下两半板)的控制方程为

本文采用双线性本构T-S 分析图1所示分层裂纹的扩展,该本构具有理论完善、简洁高效、所需测量及拟合参数较少等特点,在复合材料层合板分析中得到广泛应用.如图2所示,双线性T-S 包含线弹性加载及线性软化两个阶段,黏聚区材料点以零应力对应零相对位移起始,在损伤出现之前保持线弹性;假设界面初始刚度为一个适当的值,以保证在线弹性阶段,黏聚区上下表面重合、不会相互嵌入.界面应力满足损伤起始条件后,材料点发生线性软化;持续加载,直到应力再次为零时,裂纹发生扩展.定义临界能量释放率为本构关系曲线与相对位移轴线围成的面积.
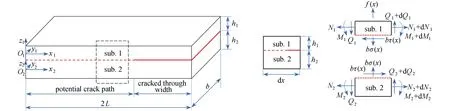
图1 层合板黏聚区微元受力分析Fig.1 Microelement stress analysis of the cohesive zone of the laminates
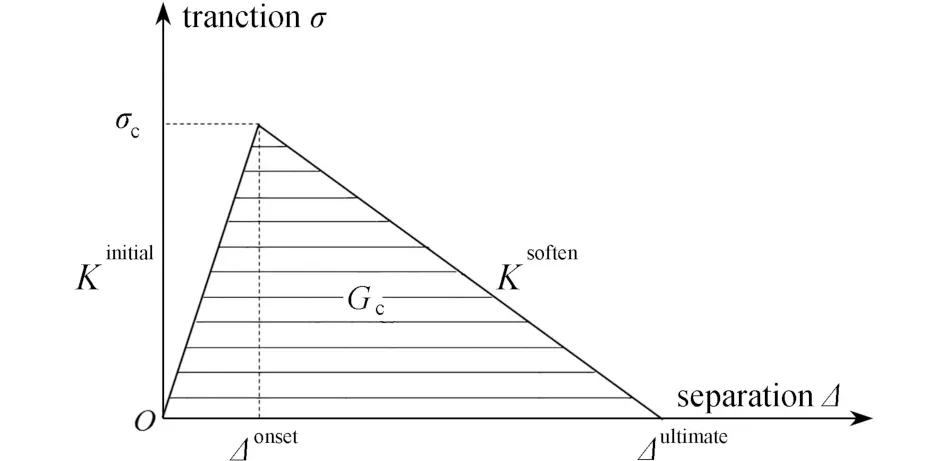
图2 黏聚区双线性本构模型Fig.2 The bilinear constitutive model for the cohesive zone
由此,基于经典层合板理论,本文建立了含一般分层裂纹的复合材料层合板的理论分析模型,包括三个部分:式(1)给出的变形协调条件,式(2)给出的平衡关系以及黏聚区的双线性本构.结合具体层合板结构及加载工况所确定的边界条件和连续性条件,可联立以上微分方程进行求解.
2 ENF试件裂纹扩展分析
为测量复合材料层合板Ⅱ型分层裂纹的临界应变能释放率,通常采用三点弯的方式对ENF试件进行加载和约束,如图3所示,ENF试件两端受简支约束,在其中间部位施加垂直于试件表面的下压载荷.加载过程中,预置于ENF试件中面的分层裂纹将会沿其中面持续向内部扩展(图3 中虚线).此外,为研究纯Ⅱ型裂纹扩展,试验过程中应保证ENF试件的上下两半板始终闭合且无法向相对位移,即式(3)中Δn=0.为满足此要求,ENF试件的铺层设计为关于中面(断裂面)对称,使得其上下半板的拉伸和弯曲刚度相同.因此,结合式(1)~(3),ENF试件裂纹扩展的控制方程可简化为
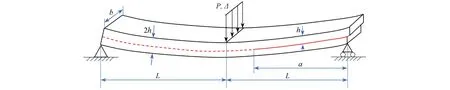
图3 ENF试件几何尺寸及加载情况Fig.3 The ENF specimen geometry and loading conditions
式中,A11s,B11s,D11s为层合板半板的拉伸刚度、耦合刚度及弯曲刚度.
2.1 位移函数



2.2 求解



图4 ENF试件加载软化阶段Fig.4 The loading softening stage of the ENF specimen
3 分析与讨论
为验证本文基于CZM 建立的分层裂纹扩展分析模型的有效性,选取文献[16]中的复合材料层合板及界面性能参数,针对给定几何尺寸的试件进行分析.ENF试件为单向复合材料(HTA6376/C)层合板,相关材料力学性能参数、试件几何尺寸分别如表1 和表2所示.

表1 ENF试件材料力学性能参数[16]Table 1 Mechanical properties of the ENF specimen[16]

表2 ENF试件几何尺寸[16]Table 2 Geometric dimensions of the ENF specimen[16]
如图5所示,本文提出的基于CZM 裂纹扩展分析模型能够有效地模拟ENF试件裂纹扩展过程,采用该模型预测的失效载荷与试验结果误差仅为5%.此外,由于考虑了黏聚区的软化过程,本文模型预测的载荷-位移曲线在初始弹性加载段之后出现非线性,预测的失效载荷优于传统的梁理论预测.由于梁理论仅在裂纹开始扩展之后引入Ⅱ型临界能量释放率,其对ENF试件失效载荷Pc的预测值偏大.加载后期,裂纹扩展主要受单参数影响,在加本文模型预测的载荷-位移曲线与梁理论结果基本重合(图5).
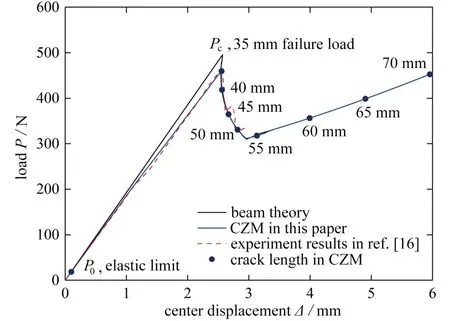
图5 本文模型与实验结果[16]及梁理论预测的对比Fig.5 Comparison of the proposed model with the experimental results[16]and the beam theory prediction
基于所提出的ENF试件分层裂纹扩展模型,本文进一步分析界面强度、断裂韧性及界面初始刚度对ENF试件载荷-位移曲线的影响.首先,界面强度对ENF试件失效前的非线性段及最大失效载荷有一定影响,如图6所示,随着界面强度增大,失效载荷增大,本文模型预测的载荷-位移曲线不断接近梁理论结果(后者仅考虑弹性阶段,假设界面强度无限大).此处,断裂韧性是影响Ⅱ型裂纹扩展的主要参数,随着的增加,失效载荷增大,如图7所示;由于梁理论未考虑黏聚区软化,其预测的失效载荷为本文模型预测的上阈值.
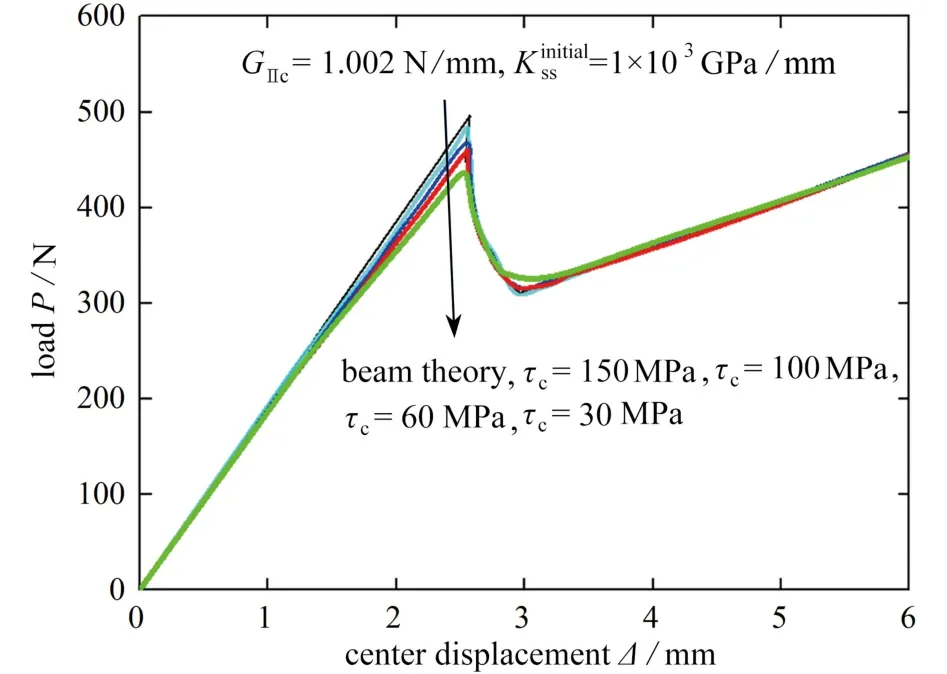
图6 界面强度对ENF试件载荷-位移曲线的影响Fig.6 Influences of the interfacial strength on load-displacement curves of the ENF specimen
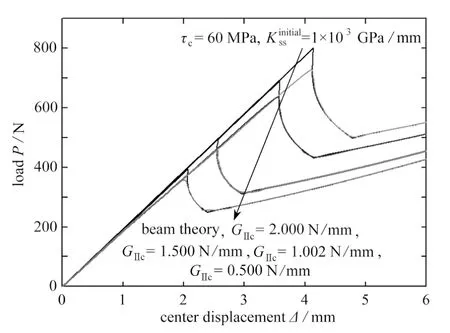
图7 断裂韧性对ENF试件载荷-位移曲线的影响Fig.7 Influences of the fracture toughness on load-displacement curves of the ENF specimen
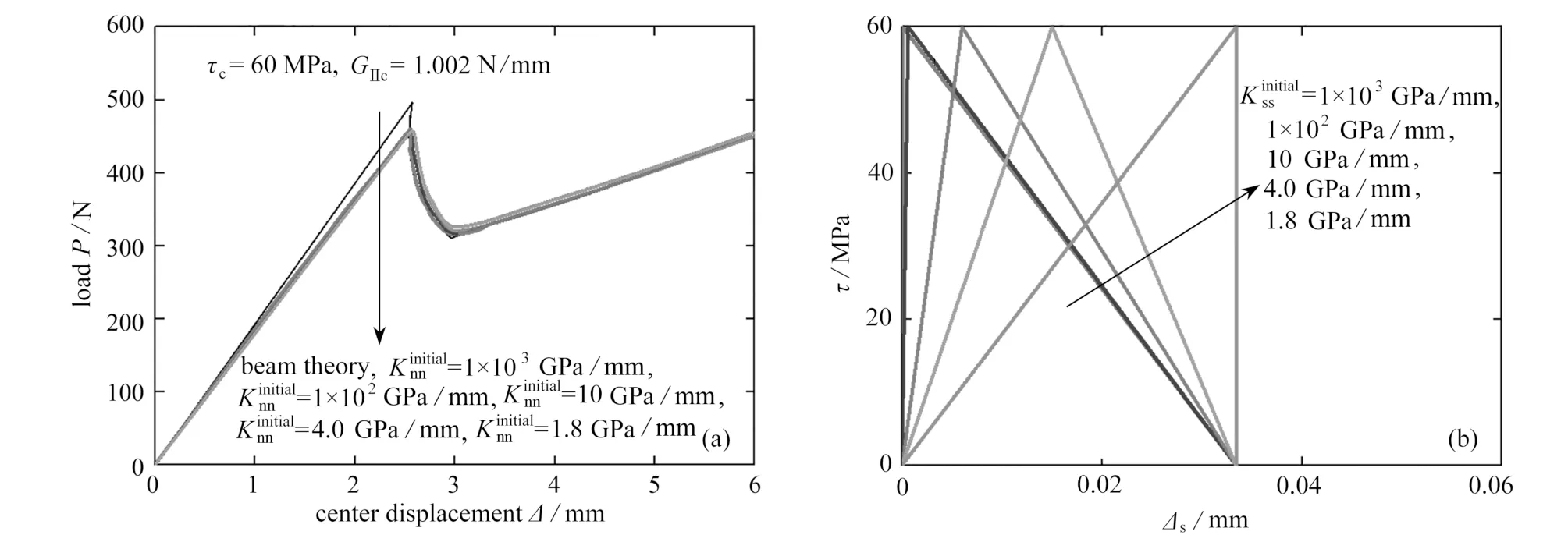
图8 Ⅱ型界面初始刚度的影响:(a)载荷-位移曲线;(b)Ⅱ型裂纹T-S 本构关系Fig.8 Influences of the initial stiffness of the mode Ⅱ interfaces:(a)load-displacement curves;(b)T-S constitutive relationships of the mode Ⅱ crack
图9 展示了ENF试件Ⅱ型裂纹黏聚区长度随裂纹扩展的变化:裂纹扩展过程中,当黏聚区尖端到达试件半长处时,lCZ呈现一定程度的减小,这与Ⅰ型裂纹的lCZ维持不变有所不同.因此,采用基于CZM 的有限元方法对含有Ⅱ型裂纹的结构进行裂纹扩展模拟时,应充分考虑裂纹长度对黏聚区长度和界面单元尺寸的影响,以保证数值模拟结果的准确性.
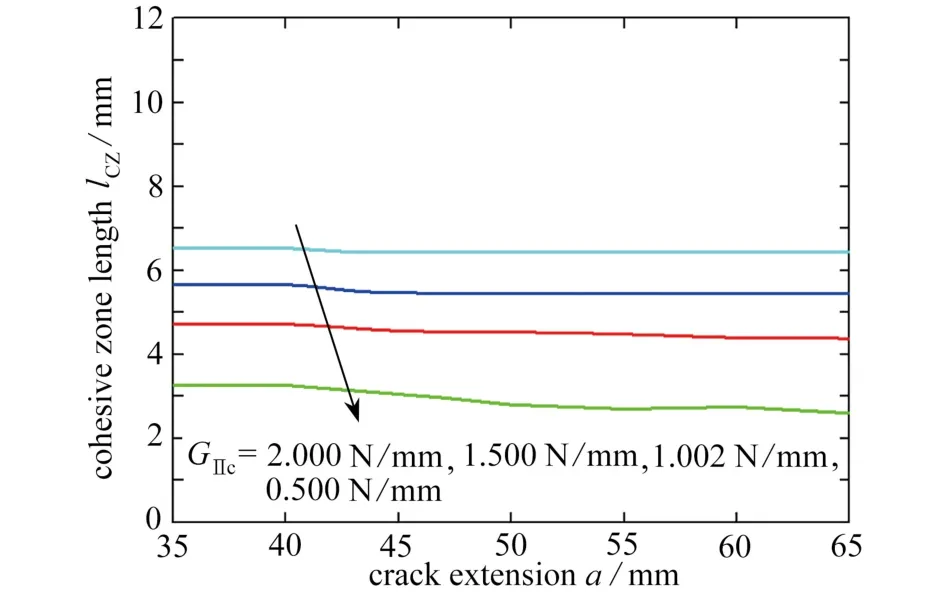
图9 Ⅱ型裂纹黏聚区长度随裂纹扩展的变化趋势Fig.9 Variation tendencies of the cohesive zone length of the mode Ⅱ crack with the crack growth
图10 给出界面参数对Ⅱ型裂纹黏聚区长度的影响,可见黏聚区长度随断裂韧性增大而增大,随界面强度增大而减小,且界面强度相较于断裂韧性对Ⅱ型裂纹黏聚区长度的影响更为明显.
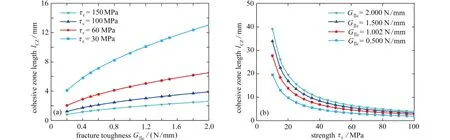
图10 界面参数对Ⅱ型裂纹黏聚区长度的影响Fig.10 Influences of interface parameters on the cohesive zone length of the mode Ⅱ crack
4 结论
基于经典层合板理论及CZM,本文建立了适用于分析纯Ⅱ型断裂ENF试件分层裂纹扩展的理论模型,且模型预测的载荷-位移曲线与试验结果吻合较好,验证了其有效性和准确性.随后,本文采用该模型,量化了界面强度、断裂韧性及界面初始刚度对ENF试件载荷-位移曲线的影响,发现界面强度主要影响试件失效前的力学行为,对裂纹扩展基本无影响;断裂韧性是影响裂纹扩展的主要参数;界面初始刚度仅影响线弹性加载段;黏聚区长度随断裂韧性增大而增大,随界面强度增大而减小;相较于断裂韧性,界面强度对裂纹黏聚区长度影响更明显;黏聚区尖端到达试件半长处时,纯Ⅱ型裂纹黏聚区的长度有一定程度的减小.本文提出的理论模型为复杂结构的分层裂纹扩展分析提供了理论依据,还为数值仿真提供了可靠的交叉检验工具.此外,后续工作应进一步分析多种Ⅱ型断裂韧性试件的裂纹扩展,如端部加载劈裂试件等,提高预测的准确性及模型的适用性.
