基于演化博弈的地铁施工人员不安全行为动态惩罚策略优化

陈赟， 刘慧琳

(长沙理工大学交通运输工程学院， 长沙 410114)

地铁施工具有施工难度大、环境复杂等特点，导致地铁施工事故时有发生[1-2]，带来人员伤亡及财产损失。根据近年地铁施工安全事故调查报告及文献统计，发现人的不安全行为引发安全事故比例高达95.38%[3]。因此，对人的不安全行为进行管控是提高施工现场安全管理水平，减少事故发生的有效途径。

近年来，国内外学者针对地铁施工人员不安全行为进行深入剖析，如影响因子、传播机理、干预措施等方面。张勇等[4]、Yu等[5]分别利用解释结构模型、系统动力学从外界环境及个体角度对不安全行为影响因素进行分析，确定关键因素；来延肖等[6]、Wang等[7]利用结构方程模型探究人的安全态度以及家庭、工作压力与不安全行为之间的作用关系；石娟等[8]发现工人群体之间会相互模仿不安全行为，利用SEIMR传播模型模拟不安全行为在群体中的传播过程；Cao等[9]对不安全行为传播规律进行探索，发现外部干预可以减少不安全行为的传播；陈赟等[10]分别从干预层面和干预类别对不安全行为进行动态仿真，发现从施工人员个体层面进行干预影响程度最大。以上研究从不同角度对施工人员不安全行为进行探析，并提出管控策略。而施工人员在既得利益与自身安全之间往往无法做出正确选择，导致对不安全行为的管控难以实施，从施工人员的行为动机角度对不安全行为进行探究也至关重要。通过博弈方法对施工安全管理的研究大多聚焦于政府、企业、地方监管[11]等方式，而内部监管的研究相对较少。在实际的施工过程中，安全管理人员有责任对施工人员进行安全监管[12]，施工人员与安全管理人员之间存在一定的利益动机，故两类群体之间的行为选择可看作一个博弈的过程[13]。且现有研究都采用静态惩罚策略[14]对不安全行为进行管控，没有从动态视角分析策略对不安全行为控制的有效性。

基于此，现从地铁施工人员和安全管理人员双方的“成本-收益”角度出发，构建以地铁施工人员与安全管理人员为主体的演化博弈模型，探究博弈双方的策略选择与行为演变过程，并利用系统动力学(systematic dynamics，SD)模型对两方博弈模型进行仿真模拟，分析静态及动态惩罚制度下不安全行为状态的转变，进而通过有效的惩罚手段，提高施工人员对安全施工的重视度，从而减少不安全的发生。

1 安全管理人员与施工人员的演化博弈模型

1.1 模型构建及相关假设

在构建不安全行为检查博弈模型之前，需要对不安全行为检查实际情况做一些假设，以此来简化演化博弈分析，对演化博弈做出如下假设。

(1)博弈主体。假定博弈主体只包括地铁施工人员和安全管理人员，且均为有限理性参与方，在信息不对称的条件下进行反复博弈，为追求自身利益最大化，寻找最佳策略。

(2)不安全行为是指在施工过程中，违反现场安全管理准则，可能导致事故发生的不正确作业习惯。

(3)假设在日常行为管理监督下，地铁施工人员与安全管理人员双方策略抽象为{安全行为，不安全行为}，{检查，不检查}。

1.2 博弈双方行为策略

不同的策略对应不同的收益成本，其中相关参数含义如表1所示。

假设x为选择安全行为的施工人员在群体中所占比例，y为选择检查策略的安全人员在群体中所占比例，其中0≤x，y≤1。

结合不同行为发生在群体中所占的比例，可以得到地铁施工人员和安全管理人员相应的收益矩阵，如表2所示。

表1 模型参数定义Table 1 Definition of model parameters

表2 博弈双方的收益矩阵Table 2 Income matrix of metro construction personnel and safety management personnel

1.3 模型分析

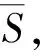
S1=y(R1-C1)+(1-y)(R1-C1)

=R1-C1

(1)

S2=y(R2-fL-C3)+(1-y)(R2-fL)

=R2-fL-yC3

(2)

=x(R1-C1)+(1-x)(R2-fL-yC3)

(3)

T1=x(-C2)+(1-x)(C3-C2)

=C3(1-x)-C2

(4)

T2=xR3+(1-x)(R3-fLk)

=R3+(x-1)fLk

(5)

=y[C3(1-x)-C2+(1-y)×

[R3+(x-1)fLk]

(6)

在演化博弈的过程中，作为有限理性的博弈双方，双方可以学习和模仿上个时间段获取更高利益的行为策略。根据式(1)～式(6)，可得到双方复制动态方程式为

(R2-fL-yC3)]

(7)

[R3+(x-1)fLk]}

(8)

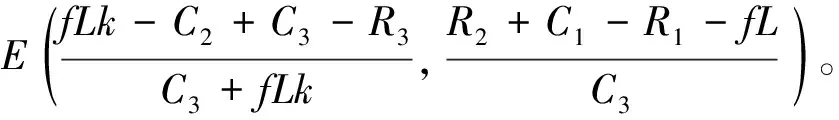
1.4 演化博弈均衡点稳定性分析

可通过雅克比矩阵鉴定均衡解是否稳定[15]，为此，通过前文求得雅可比矩阵A如式(9)所示。

根据局部均衡解稳定分析法的判断准则，当均衡解对应的DetJ>0且TrJ<0时，则这个均衡解为演化稳定策略(evolutionary stable strategy，ESS)，即博弈模型处于稳定状态[15]。对以上5个均衡解代入矩阵中进行求解，由于参数较多，均衡解表达式过于复杂，所以稳定性难以确定。

2 系统动力学模型构建与仿真

为进一步研究博弈模型行为的演化机理，利用系统动力学，以地铁施工人员与现场安全管理人员双方选择不同策略时的复制动态方程为基础，构建地铁施工人员不安全行为演化博弈SD模型，模拟仿真系统变化时对双方策略选择演变过程的影响。

2.1 SD模型反馈图构建

根据上述地铁施工人员不安全行为博弈模型分析，利用Vensim PLE 6.3对其建立SD模型，构建的SD模型由施工人员选择安全行为占群体比例及安全管理人员进行检查占群体比例2个水平变量，施工人员的安全行为变化率和安全管理人员检查变化率2个速度变量，以及C1、C2等15个辅助变量构成。SD模型如图1所示。

2.2 SD模型初始仿真分析

根据文献[16]以及实际情况对相关参数进行赋值，设置初始参数为：initial time=0，final time=100，time step=0.031 25，units for time：week。设置15个辅助变量的初始值置：C1=3，C2=1，C3=4，R1=5，R2=4，R3=1，L=5，f=0.2，k=0.6。基于前文分析得到的变量关系[式(1)～式(8)]确定SD模型中流率公式及其涉及的中间变量。

(9)

图1 施工人员不安全行为演化博弈系统动力学模型Fig.1 Dynamic model of evolutionary game system for unsafe behavior of construction workers

2.2.1 初始仿真

初始阶段，博弈双方采用均衡解，将5个均衡解输入Vensim PLE 软件，进行数据仿真，其结果如图2所示。

图2 博弈双方行为仿真结果Fig.2 Simulation results of behaviors of both parties in the game

当双方采取纯策略A时，安全管理人员选择“不检查”时，而地铁施工人员作为有限理性人，出于对自身利益的考虑，其最佳策略是进行“不安全行为”，维持现状不变；当博弈双方采取纯策略B时，即所有的施工人员选择“不安全行为”，管理人员选择“检查”策略，也就是说即便施工人员先前还处于一种不利地位，在没有通过学习而选择新策略之前，双方策略选择还处于稳定状态，纯策略C同理；当博弈双方采取纯策略D时，安全管理人员选择“检查”时，施工人员考虑到自身利益，同时还要承担起相应的安全责任，最佳策略是选择“安全行为”。

2.2.2 纯策略稳定性仿真

下面对某个体更改策略后系统的最终稳定状态进行分析。以纯策略均衡解A为例进行验证，将安全管理人员检查的比例由y=0调整为y=0.05再次进行仿真，结果如图3所示。

图3 纯策略A(y→0.05)仿真结果Fig.3 Simulation results of pure strategy A(y→0.05)

安全管理人员中某个体改变策略后，原均衡状态就会发生改变，安全管理人员检查概率由0向1发生转变，双方策略由A逐步演化至B。发生该情况的原因可能是，当安全管理人员中的某个个体改变策略后，检查发现了地铁施工人员不安全，对其进行惩罚获得了更高的收益，则该群体中的其他个体开始模仿该行为，从而导致安全管理人员的检查趋势不断加强，最后演变为图3的状态。则初始均衡解A不稳定。同理，可得到其他3个纯策略解都不是演化稳定均衡解。

2.2.3 混合策略稳定性仿真

由图2得到混合策略均衡解E也是一种相对稳定的状态。同样，对策略微小改变，再次进行模拟，结果如图4所示。线呈振荡趋势，表明安全管理人员检查与施工人员不安全行为的策略选择是不断震荡变化且没有收敛的，双方采取不是均衡值时，另一方会依据对方的策略来调整自己的策略，随着博弈时间和博弈次数的增加，双方策略变动较大，系统稳定存在不确定性。

仿真结果表明，混合策略以及纯策略的均衡点具有不稳定性，只有任意一方的策略选择发生微小变化，原策略会趋向于其余策略稳定，则不存在稳定策略，说明施工人员的策略选择具有波动性。

图4 混合策略E(y→0.2)仿真结果Fig.4 Simulation results of mixed strategy E(y→0.2)

3 不安全行为检查系统的稳定性控制与优化

根据上述博弈结果分析中可知，5个策略都处于不稳定状态，在这个波动状态下，安全管理人员难以合理地对施工人员不安全行为检查，不安全行为难以得到及时有效的控制。因此，有必要对如何稳定该博弈系统的控制策略进行研究。

3.1 一般惩罚策略

研究安全管理人员的惩罚力度对施工人员不安全行为的影响，通过改变系统中对施工人员不安全行为的惩罚力度，将对施工人员的惩罚力度C3=4改变为C3=5、C3=6，初始策略选择设定为x=0.5，y=0.5，图5(a)、图5(b)分别表示在对施工人员不同惩罚力度下，安全管理人员和施工人员的策略选择。

从图5(a)、图5(b)的仿真结果可知，增大对不安全行为的惩罚力度，安全管理人员的检查概率以及施工人员的安全行为概率上升，上升的幅度也更大，且存在有规律的波动性。可以发现，仅提高惩罚力度，可以增加地铁施工人员安全行为的概率，谷值和峰值均有提高，但是该策略只在短期内有效，施工人员会因为惩罚力度的增大而选择安全行为，但这种情形不能得到维持，随着时间的增长，博弈双方的行为选择还是存在一定的波动性，这使得管理人员做出错误的预计，从而错误选择策略，而过于严厉的惩罚力度引发施工人员的报复行为，可能导致安全偏离行为的发生[17]，在制定与实施惩罚制度时存在局部限制性。

图5 一般惩罚情景下博弈双方行为仿真结果Fig.5 Simulation results of behaviors of both players in the game under general punishment scenario

3.2 动态惩罚策略

在对施工人员不安全行为的惩罚C3为固定值的基础上，惩罚力度的增大确实可以使施工人员选择安全策略的概率上升，但是博弈双方的策略选择仍处于频繁波动的状态，施工人员不安全行为没有被有效地约束。仅通过提高惩罚力度来减少不安全行为不可行，因此需要为安全管理人员找到一个更加合理有效的惩罚策略，同时避免博弈演化过程的波动性。

因此，采用动态惩罚函数，设置不安全行为惩罚程度随着不安全行为比率的上升而提高，当施工人员选择不安全行为时，增大事故发生的可能性，而事故的严重程度也会增大。所以，认为施工人员的不安全行为概率与事故严重程度存在正相关关系，则可以表示事故的严重程度。因此，假设施工人员受到的惩罚由原来的常数C3变为动态惩罚C3=c3(1-x)，引入中间变量c3，c3表示罚款的最高标准，设置初始值C3=4(1-x)，保留其他参数与上述静态惩罚策略一致。设置双方策略选择的初始值为：(x,y)=(0.5,0.5)、(x,y)=(0.2,0.8)，对着两种情景进行仿真，结果如图6(a)、图6(b)所示，可以发现，在动态惩罚下，即使双方在不同的初始策略下，演化博弈不断变化，最终结果都稳定在(0.36，0.39)，较好地抑制了双方博弈中的不断波动，使两方策略收敛于一点。

通过仿真结果可知，在动态惩罚策略下，该演化模型最终稳定于均衡解x*=(0.36,0.39)中，将均衡解带入博弈模型中进行进一步验证，若两者结果相同，则证明此解是有效的。

将C3=4替换为C3=c3(1-x)，得到新的复制动态方程为

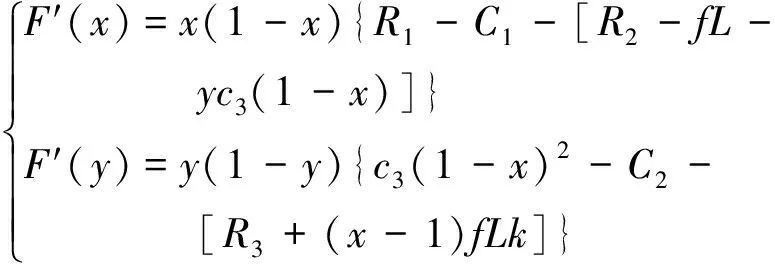
(10)

令[F′(x),F′(y)]=0, 0≤x,y≤1，得到该方程组的5个均衡解为：A(0,0)，B(0,1)，C(1,0)，D(1,1)，E(0.36,0.39)。

将A～E带入新复制动态方程的雅可比矩阵，由表3可知，E点满足ESS稳定性条件，表明E点是系统的稳定性解。

图6 动态惩罚策略仿真结果Fig.6 Simulation results of dynamic punishment strategy

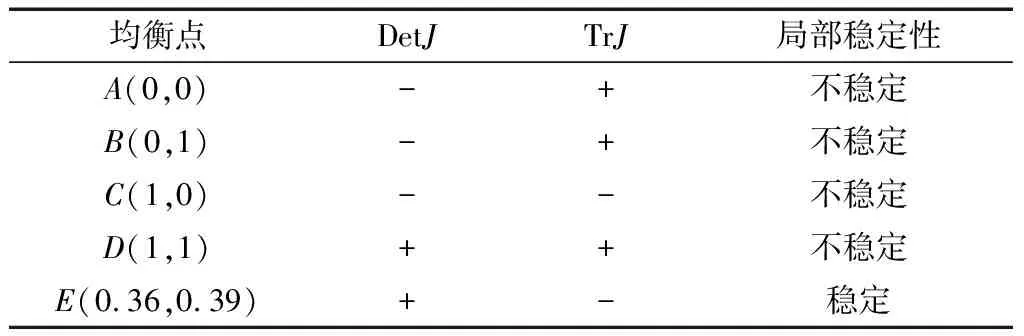
表3 管理人员与施工人员演化博弈均衡点稳定性判定Table 3 Stability judgment of equilibrium point of evolutionary game between managers and constructors

3.3 优化动态惩罚策略

综上所述，在动态惩罚策略下，可以降低博弈策略选择的波动性，从而达到稳定。上述分析结果表示虽然动态惩罚策略可以使博弈模型达到均衡状态，但在实际施工中，仅有36%的施工人员选择安全行为概率及39%的安全管理人员会对施工人员进行检查，并不是理想中的最优稳定策略，因此需要对动态惩罚策略进行优化，将安全管理人员对进行不安全行为的施工人员的罚款与两者选择概率和进行安全行为的成本相联系。优化动态惩罚方案为C3=c3(1-x)+C1/y，其中c3代表相应的惩罚系数，设置为4，参数保持与前文一致。

在优化的动态惩罚情况下进行仿真，考虑初始策略(x,y)=(0.5,0.5)、(x,y)=(0.2,0.8)，仿真结果如图7(a)、图7(b)所示。

由仿真结果可得，博弈的演化过程大致收敛于P(1，0)，说明优化动态惩罚方案对系统进行了优化，可以有效地抑制双方策略的波动，提供了最优稳定策略，此时双方博弈的策略选择达到了理想状态，即安全管理人员以较小的比率对其检查管理，同时地铁施工人员会遵守正确操作准则。将优化动态惩罚机制代入博弈模型进行验证，解得雅克比矩阵B为

B=

(11)

代入P(1，0)求得特征值λ1=-18、λ2=-2，λ1<0，λ2<0。

因此，P(1，0)是该模型的稳定策略，验证结果与仿真结果吻合。在优化的动态惩罚下，博弈双方行为选择达到了稳定，施工人员几乎都选择安全行为作为最优策略，有效地减少了不安全行为的发生。

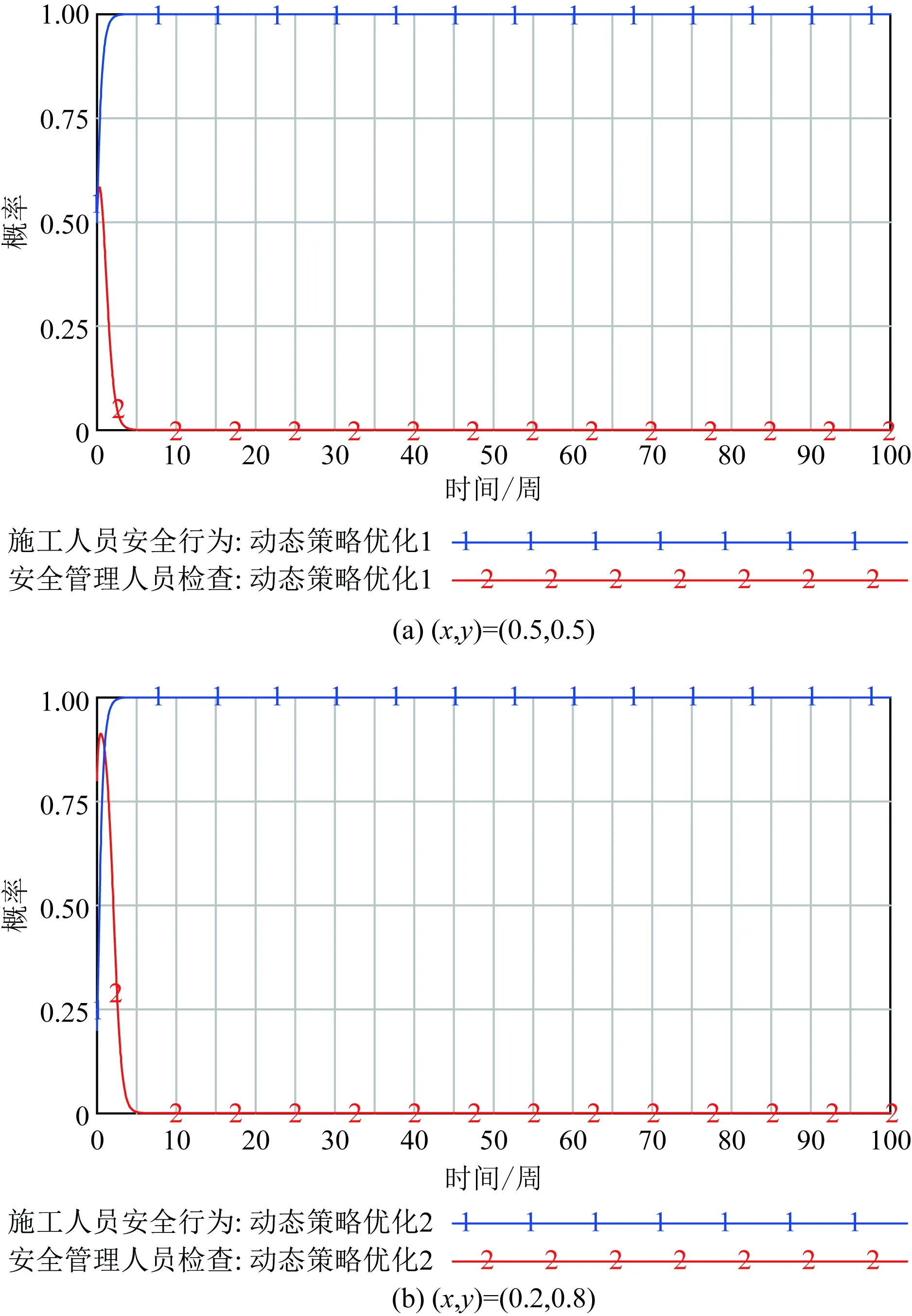
图7 优化动态惩罚策略仿真结果Fig.7 Simulation results of optimizing dynamic punishment strategy

4 结论

(1)施工人员与安全管理人员在一般条件下无法达到稳定的均衡解，单纯地加大惩罚力度只能在短期内有效地减少不安全行为的发生，但博弈双方的行为依然不断上下波动，且幅度增大，导致安全管理人员在后期对施工人员的管理更加困难，由于双方的行为选择是不断循环且进化的，地铁施工人员容易找到管理中的漏洞，在此条件下，管理人员应对惩罚制度及时调整，为减少不安全行为提供有力的管理。

(2)引入动态惩罚后并对其进行优化后，安全管理人员可以将罚款金额与不安全行为比例及不安全行为收益挂钩，施工人员与安全管理人员的不稳定状态得到抑制，达到稳定状态，为安全管理人员实现有效检查提供了最优的策略选择，以较小的比率对其监督管理可以有效防止不安全行为的发生。

(3)以上结果为地铁施工人员的安全管理机制的设计与应用提供了思路，提供了重要理论和实践意义，模型参数设定基于文献参考与专家咨询得到，与现实可能存在差异，未来将基于实际现场数据进行仿真研究，以得到更具有说服力的结果。