基于车辆车载诊断数据的山地城市道路异常驾驶行为空间分布特征
2022-06-14王玉婷张梦歌彭博蔡晓禹荣晓楠
王玉婷, 张梦歌, 彭博*, 蔡晓禹, 荣晓楠
(1.山地城市交通系统与安全重庆市重点实验室, 重庆400074; 2. 重庆交通大学交通运输学院, 重庆 400074)
异常驾驶行为会导致车辆冲突加剧,现有交通安全风险研究大多是事故后的数理统计分析,难以准确刻画事故发生前的交通运行状态;并且目前大量的异常驾驶行为数据并未得到充分挖掘。目前国内外对驾驶行为的研究主要分为驾驶行为的影响因素、驾驶行为与道路交通安全关系等方面。
在驾驶行为影响因素方面,Shinar[1]以驾驶员特性(包括性别、年龄等),以及车上有无乘客、车辆类型、时间等作为影响因素,研究发现男性和年轻驾驶员比女性和年老驾驶员更易产生激进驾驶行为;高峰时间段驾驶人员产生激进驾驶行为的可能性更大。Lee等[2]利用车载传感器研究识别潜在的激进驾驶行为。庄明科等[3]通过问卷调查方式采集数据分析产生攻击性驾驶的驾驶员相关因素,发现A型人格的驾驶员更容易产生攻击性驾驶,在驾驶过程中,驾驶员的态度、技术对车辆的熟悉程度会不同程度地影响风险驾驶行为,驾驶技术越好、对车辆越熟悉的驾驶员可能出现风险驾驶行为的频数会更高;Satoshi等[4]分析驾驶时间与驾驶行为之间的关系,认为连续驾驶导致的疲劳驾驶将影响车辆制动时速度下降量和减速距离。国内外学者利用模拟驾驶实验方法获得驾驶员不同状态下的异常驾驶行为数据,研究了疲劳驾驶[5-6]、负面情绪驾驶[7-9]等。
在驾驶行为与道路安全关系方面,蔡晓禹等[10]基于车辆车载诊断(on-board diagnostics,OBD)驾驶行为数据及信息熵理论,提出了城市道路交通安全风险预估方法,并建立了风险等级阈值计算方法。徐进等[11]根据驾驶员制动行为与车辆表现出的航向角和车速等信息之间的关系,分析驾驶员制动行为对安全性影响,研究表明,车辆行驶方向的稳定性与制动力度具有显著影响,而与驾驶员动作时间影响很小。李英帅等[12]、周颖等[13]通过分析信号交叉口车辆换道过程行为指标与道路安全风险性之间的关系,认为纵向速度、车辆间距、驾驶倾向3个因素与车辆发生冲突风险之间具有显著影响性。关于异常驾驶行为与交通安全事故的关联性相关研究表明:同一条道路上不同路段的异常驾驶行为率随交通事故数的增加而增加,其变化趋势基本一致[14-15]。因此,异常驾驶行为率可以表征道路交通安全状态。
国内外对于驾驶行为的研究较多,分析现状驾驶行为数据研究成果,主要有以下特点:一是研究成果主要以驾驶员心理、生理等角度分析驾驶行为,建立模型分析多个道路条件与异常驾驶行为的关系相关研究成果较少;二是大多数驾驶行为数据通过模拟实验或实际操作实验获取,数据量有限。
2014年以来,基于车辆的车载诊断(OBD)的数据采集技术和设备得到了发展[16-17],目前在研究小汽车出行行为特征[17]、驾驶行为[18-20]、车辆道路排放[21]、事故率预测[22]等方面得到了广泛的应用。现以车联网OBD异常驾驶行为数据为基础,选取道路坡度、弯度、公交站和开口为影响因素,以重庆市主城区6条主干路为研究对象,建立急加速、急减速、急转弯和超速行为空间分布规律模型。
1 数据准备
1.1 OBD数据提取与处理
车辆OBD原始数据包含11种类型数据,在数据使用之前需根据研究内容在原始数据中提取可用数据。主要基于车辆全球定位系统(global positioning system,GPS)数据和驾驶行为数据两种类型数据进行研究,因此,主要选取了重庆市6条主干道2018年5月16—21日的异常驾驶行为数据。
1.2 路段选取及类型划分
为分析城市主干路道路的坡度、弯度、公交站和开口与异常驾驶行为之间的关联性,依据车道数、中央分隔带类型等道路条件不变原则,选取重庆市6条主干道,并划分成不同类型的路段,如表1所示。
2 基于道路条件的异常驾驶行为影响因素分析
2.1 坡度的影响
根据相关研究成果,坡度与道路交通安全、车辆异常驾驶行为关系密切[23-24],主要分析坡度与异常驾驶行为率的联系。
由图1可得,异常驾驶行为中急减速占比最高,平坦路段发生频率高于陡坡路段。相对于陡坡路段,驾驶员更容易在平坦路段处放松警惕,因此更容易产生紧急刹车、急减速行为。
2.2 弯度的影响
山地城市道路中通常会有转弯半径较小的路段,急转弯等异常驾驶行为常有发生,但急加速、急减速以及超速等异常驾驶行为在弯道处的发生频率低于直线路段,直线路段、弯道路段内异常驾驶行为率如图2所示。

表1 城市道路路段分类Table 1 Classification of urban road sections
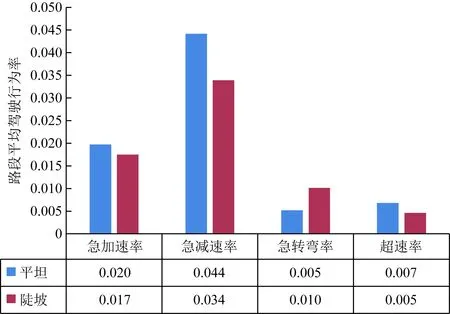
图1 坡度与异常驾驶行为的关系Fig.1 Relationship between gradient and abnormal driving behavior
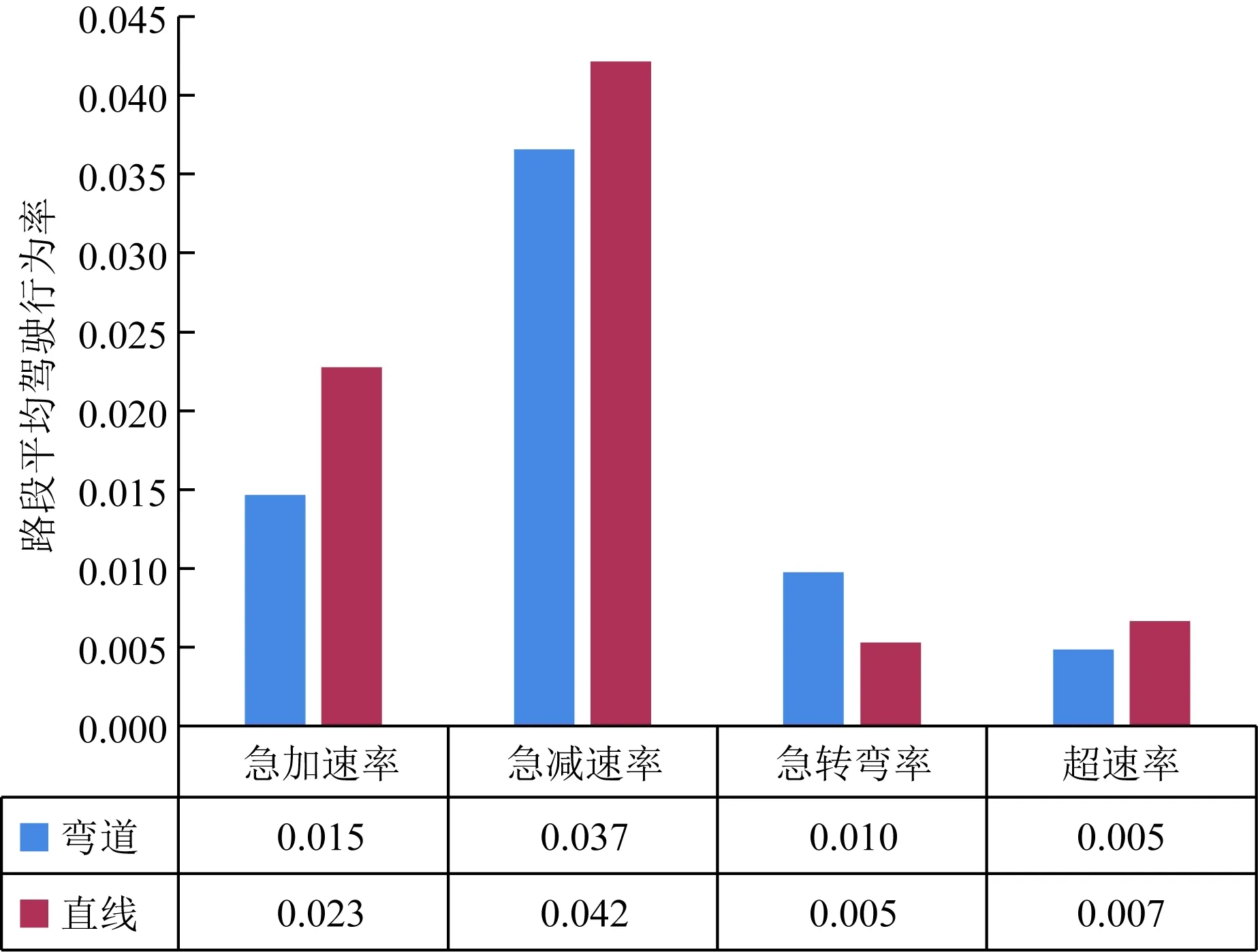
图2 弯度与异常驾驶行为率的关系Fig.2 Relationship between curve and abnormal driving behavior rate
2.3 开口的影响
由图3可知,有信控开口路段的急加速和急减速频率最高,信控开口对急加速、急减速行为的影响较大;此外,开口对急转弯频率影响较小;对超速行为的发生无显著影响。
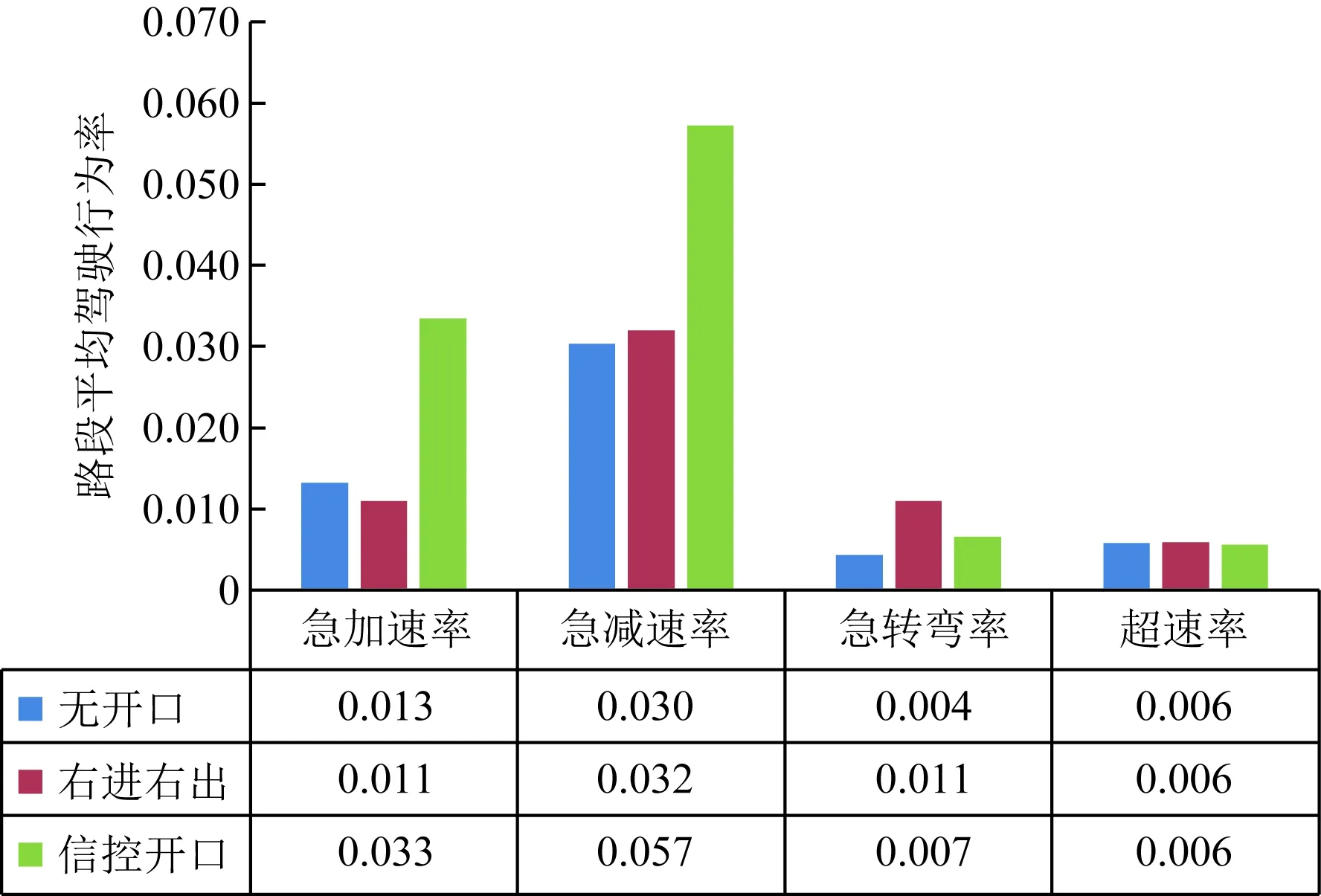
图3 开口对异常驾驶行为频率的关系Fig.3 The relationship between opening and frequency of abnormal driving behavior
2.4 公交站的影响
驾驶员在通过公交站路段时,对道路安全风险感知的程度不同,采取的驾驶行为措施也不同,公交站的布设对驾驶行为有一定影响。
由图4可知,公交站的布设对急加速、急减速、急转弯行为的影响较为明显,对超速行为影响不大。
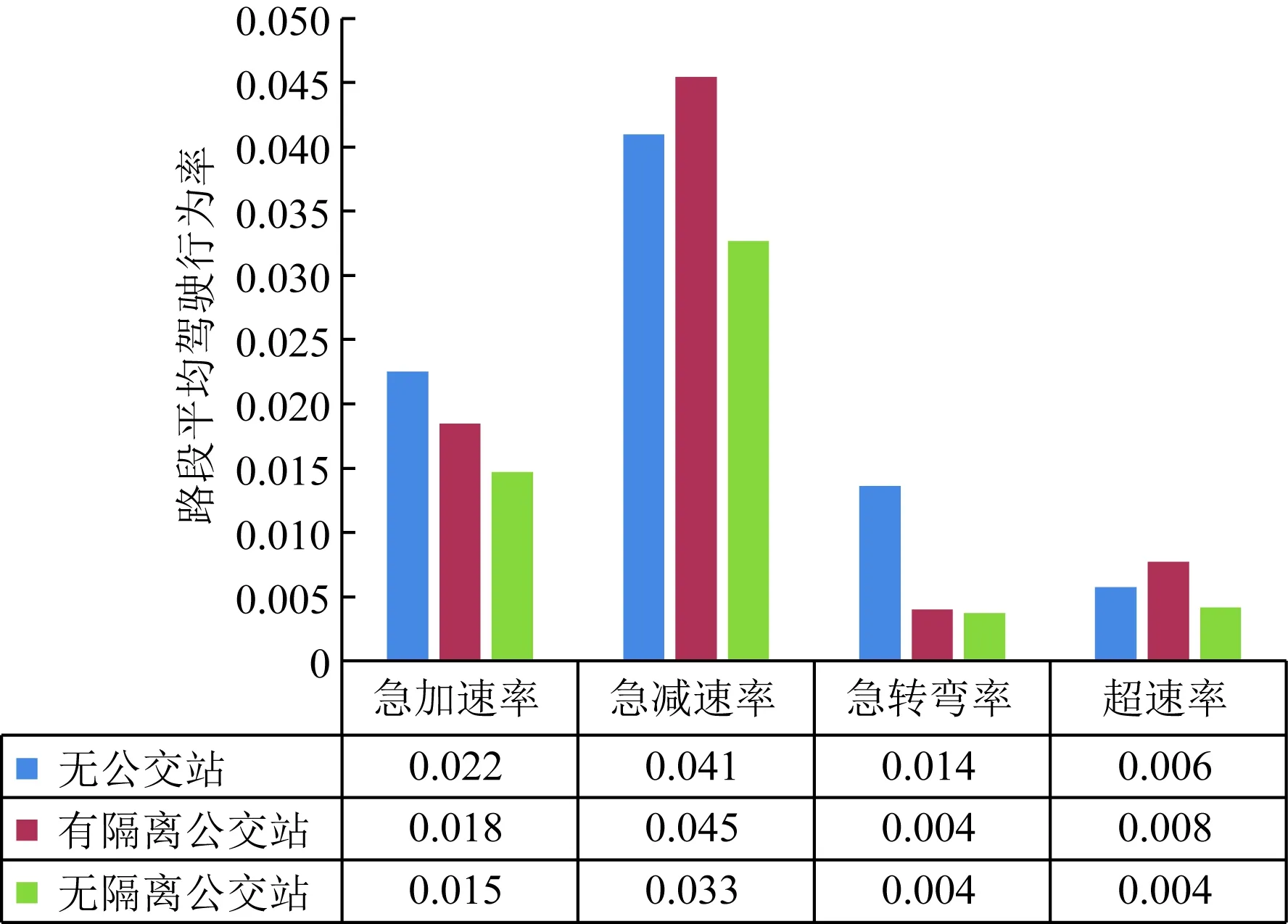
图4 公交站对异常驾驶行为率的影响Fig.4 Effect of bus station on abnormal driving behavior rate
3 异常驾驶行为空间分析模型
异常驾驶行为的空间分布特征需利用合适的数学模型进行描述,经拟合检验,泊松回归模型可用于描述单位容积内某事件发生的频数分布,零膨胀回归模型可刻画样本数据具有“零值过多”,且服从某种离散分布的计数因变量随自变量变化而变化的关系模型。因此,拟基于这两类模型展开研究。
3.1 泊松回归模型
Possion回归模型常常用于分析服从Possion分布的某事件发生次数(频率)与其解释变量之间的关系。
回归系数β的估计值通常用牛顿-拉夫森(Newton-Raphson)迭代法进行估计,实际应用中,通常使用统计软件编程实现。
3.2 零膨胀回归模型
在实际的数据统计计数过程中,基本上都是非负整数,频率分布范围为0~1,但不可否认的是,很多现象存在计数为0的情况,即该事件在统计时间段内没有发生,如事故发生次数、火灾发生次数等。
零膨胀回归模型的基本思想为:将事件计数(频率)分为两部分,一部分对应事件发生次数为0,该部分随机变量取值为0,认为研究对象处于非风险状态或低风险状态;第二部分为事件发生次数不为0,该部分随机变量取值为事件发生次数(频率),在某种解释变量影响下,事件发生次数服从泊松分布或负二项分布等。零膨胀回归可认为是零值及一个服从泊松分布或负二项分布等某个离散分布的数据集的混合分布。
3.3 变量说明及驾驶行为频率统计
3.3.1 变量说明
定量变量直接通过数据表示,定性变量需量化表示,如表2所示。
3.3.2 驾驶行为频率描述统计
根据所选路段急加速、急减速、急转弯和超速行为的连续6 d数据,利用SPSS对异常驾驶行为发生次数描述统计,如表3所示。
由表3可知,急加速发生次数平均值为1.07次,标准差为1.21,方差为1.47,方差约等于均值;急减速发生次数平均值为2.81次,标准差为2.24,方差为5.03,方差同样约等于均值,因此急加速、急减速行为发生次数没有离散现象,均适宜采用Possion回归模型。
急转弯平均每天发生0次的路段占研究路段的71.65%,超速行为平均每天发生0次的路段占研究路段的62.99%,二者零出现的次数较多,因此认为急转弯、超速频率数据出现零膨胀现象,方差与均值相差不大,适宜采用零膨胀Possion回归模型。

表2 变量说明Table 2 Variable declaration

表3 异常驾驶行为描述统计Table 3 Abnormal driving behavior description statistics
3.4 模型分析结果
3.4.1 模型拟合优度
利用SAS9.2软件中的genmod过程对样本路段建立Possion回归模型、负二项回归模型和零膨胀模型,模型拟合优度结果如表4所示。
由表4可以看出,急加速率、急减速率中Possion回归模型的AIC、BIC指标均小于负二项回归模型,认为采用Possion回归模型较好;急加速率、急减速率偏差统计量的值与自由度的比值约等于1,且根据Pearsonχ2值与χ2临界分布表可知,急加速率、急减速率观测数据与泊松预测分布之间无显著性差异,泊松回归拟合度良好。
对于急转弯频率和超速率来说,零膨胀回归模型的检验指标值SBC收敛于自由度为6的χ2分布,这两类频率分析的ZIP模型和ZINB模型的统计指标值对应χ2分布表中P<0.01,应拒绝原假设,认为样本超速数据存在明显的零膨胀现象,因此选择零膨胀模型是合理的。
从急转弯率的AIC指标来看,AICZIP>AICZINB,且急转弯发生次数的方差值是均值的21倍,这两种情况均表明ZINB回归模型拟合程度优于ZIP回归模型。
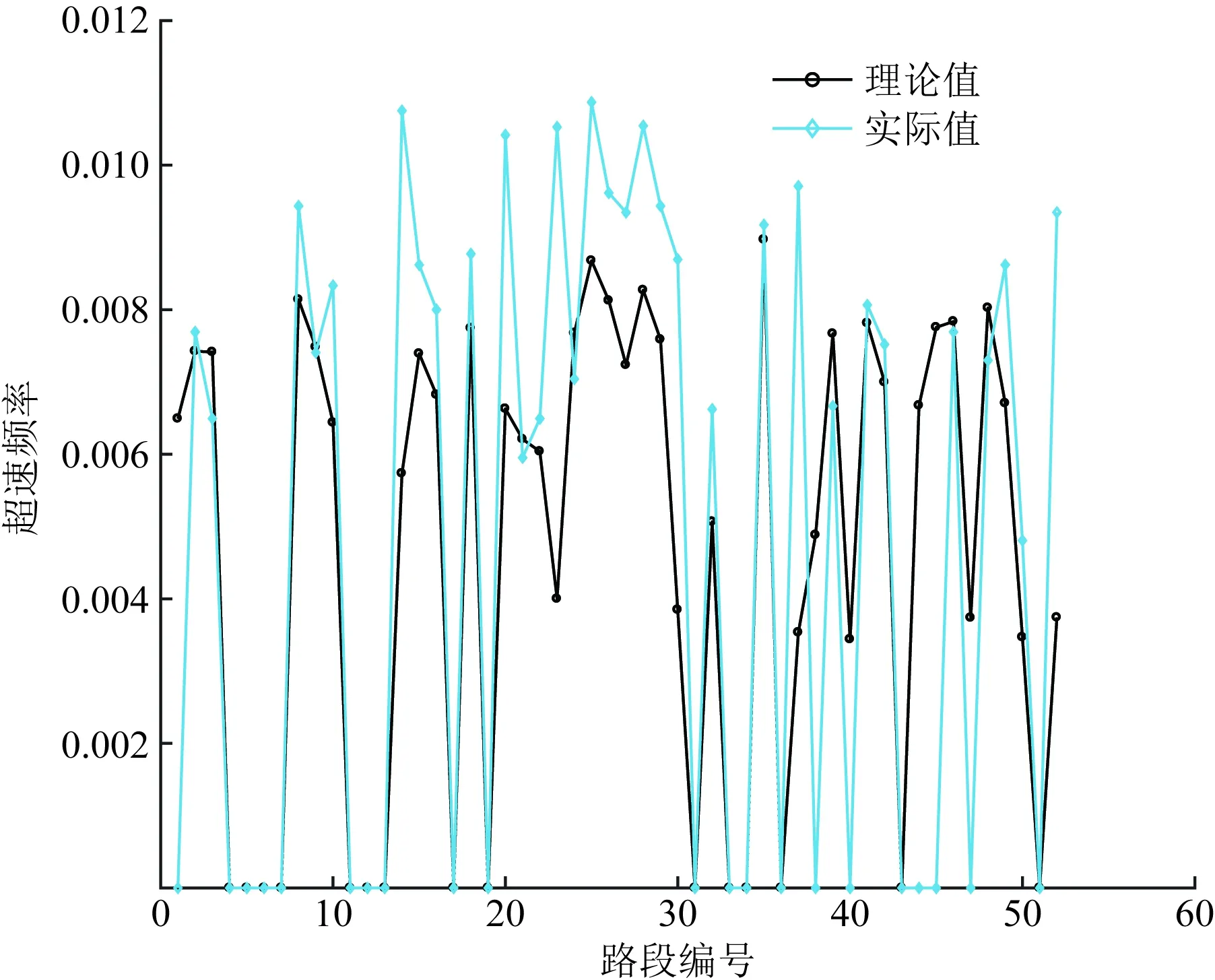
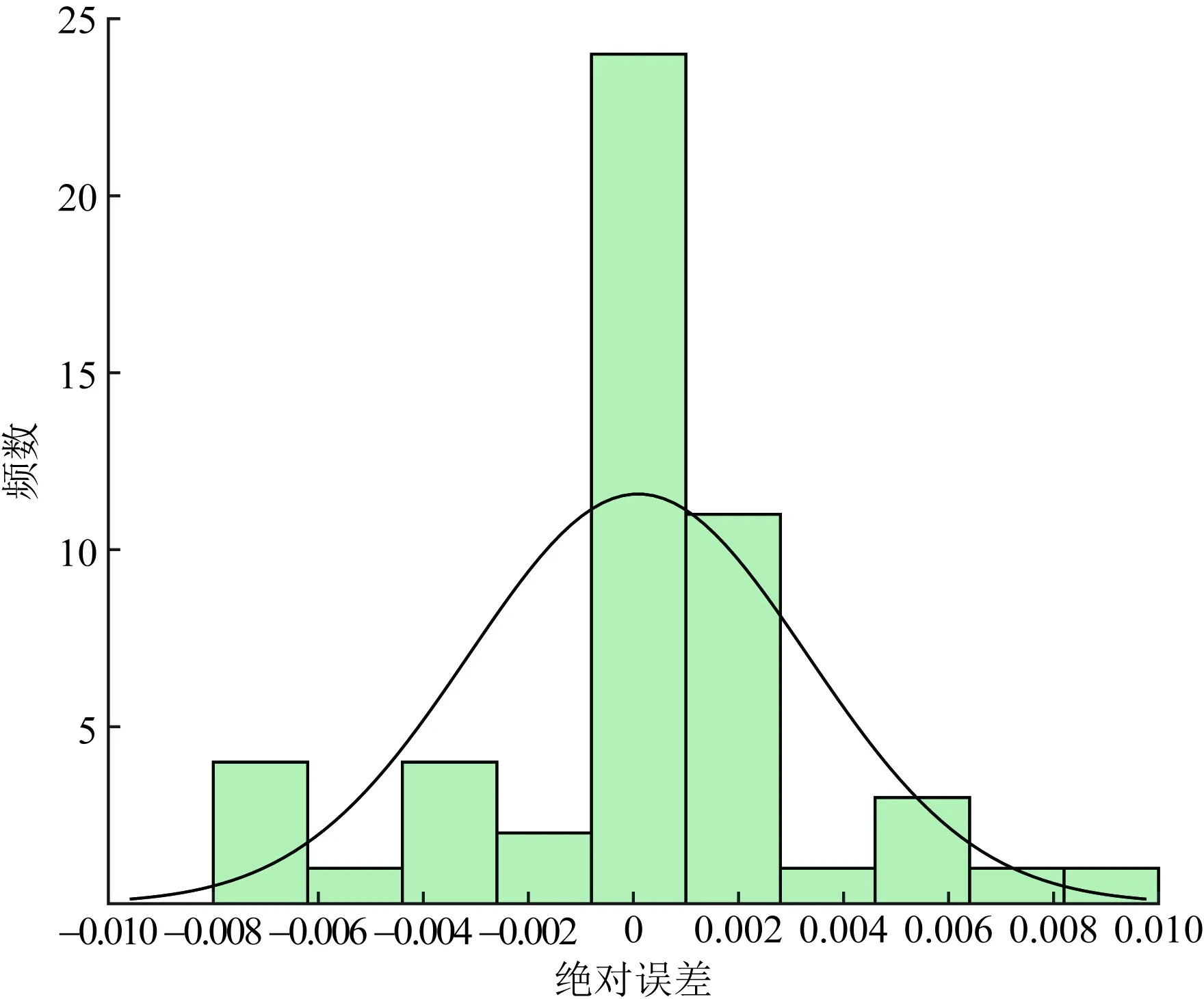
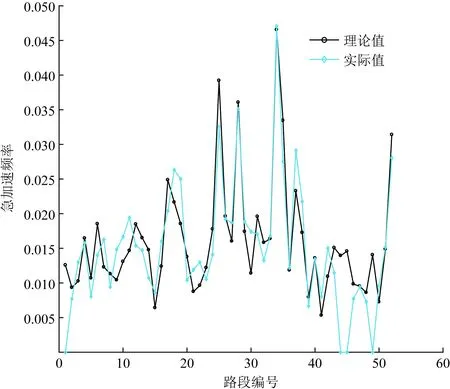
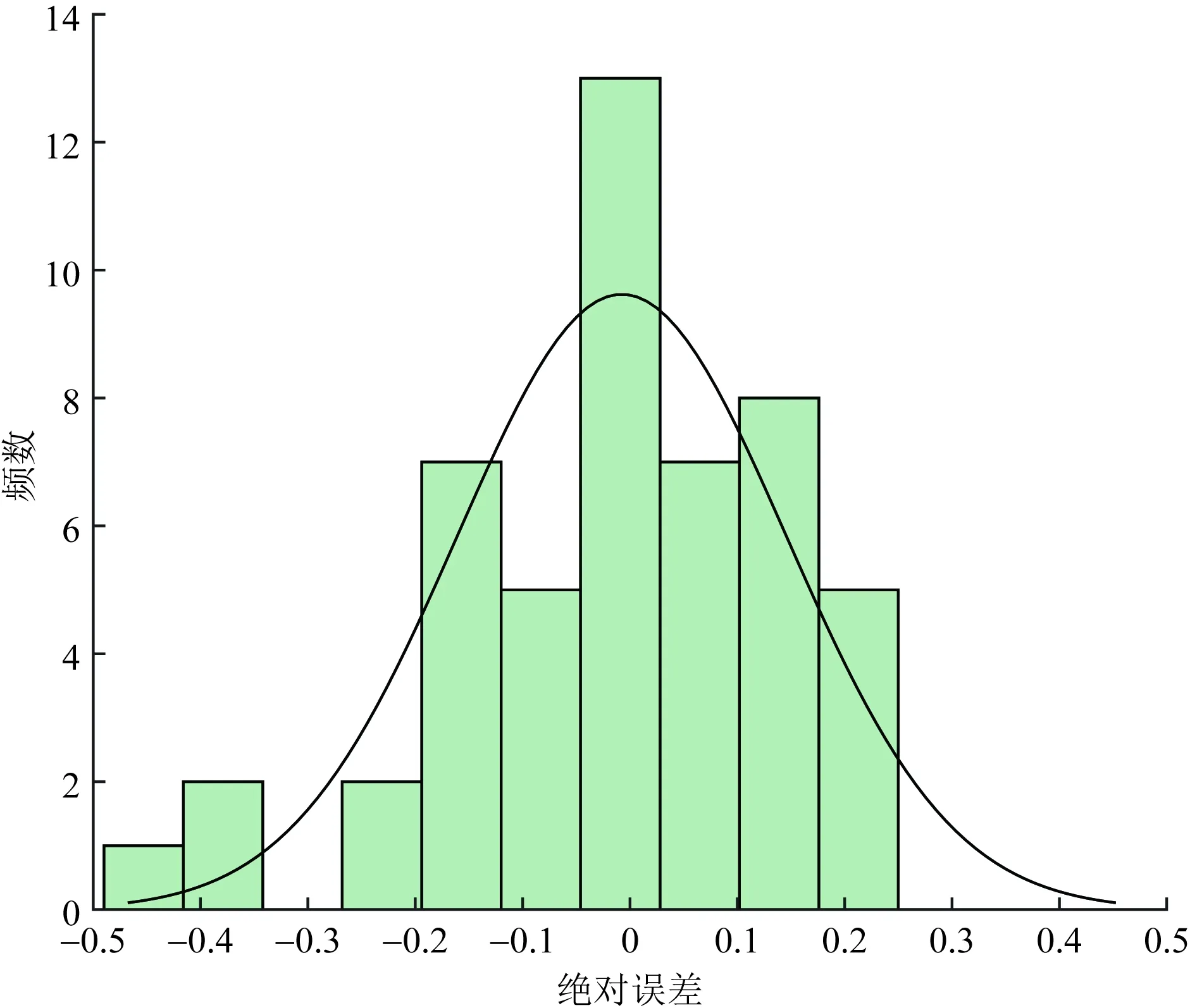
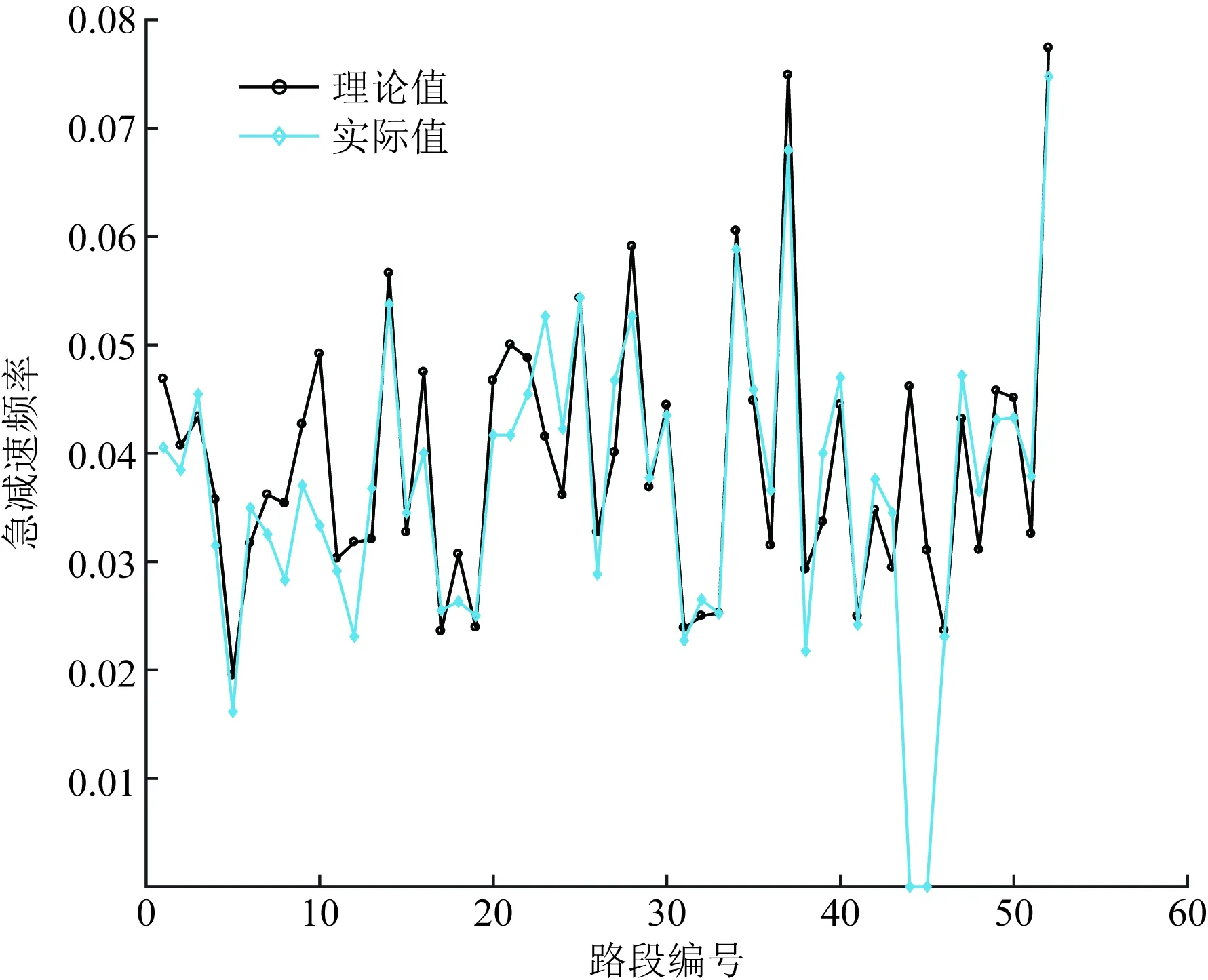
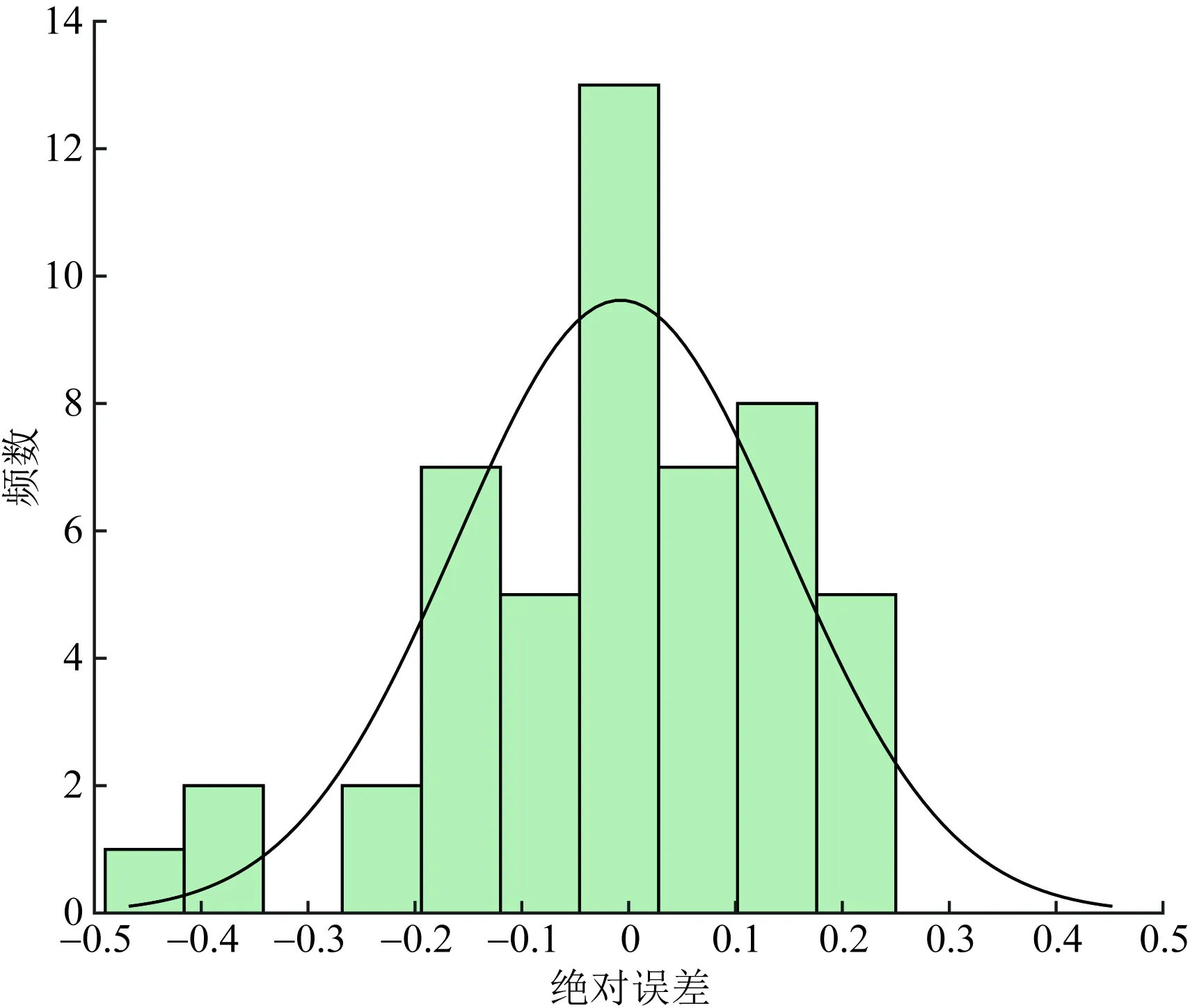
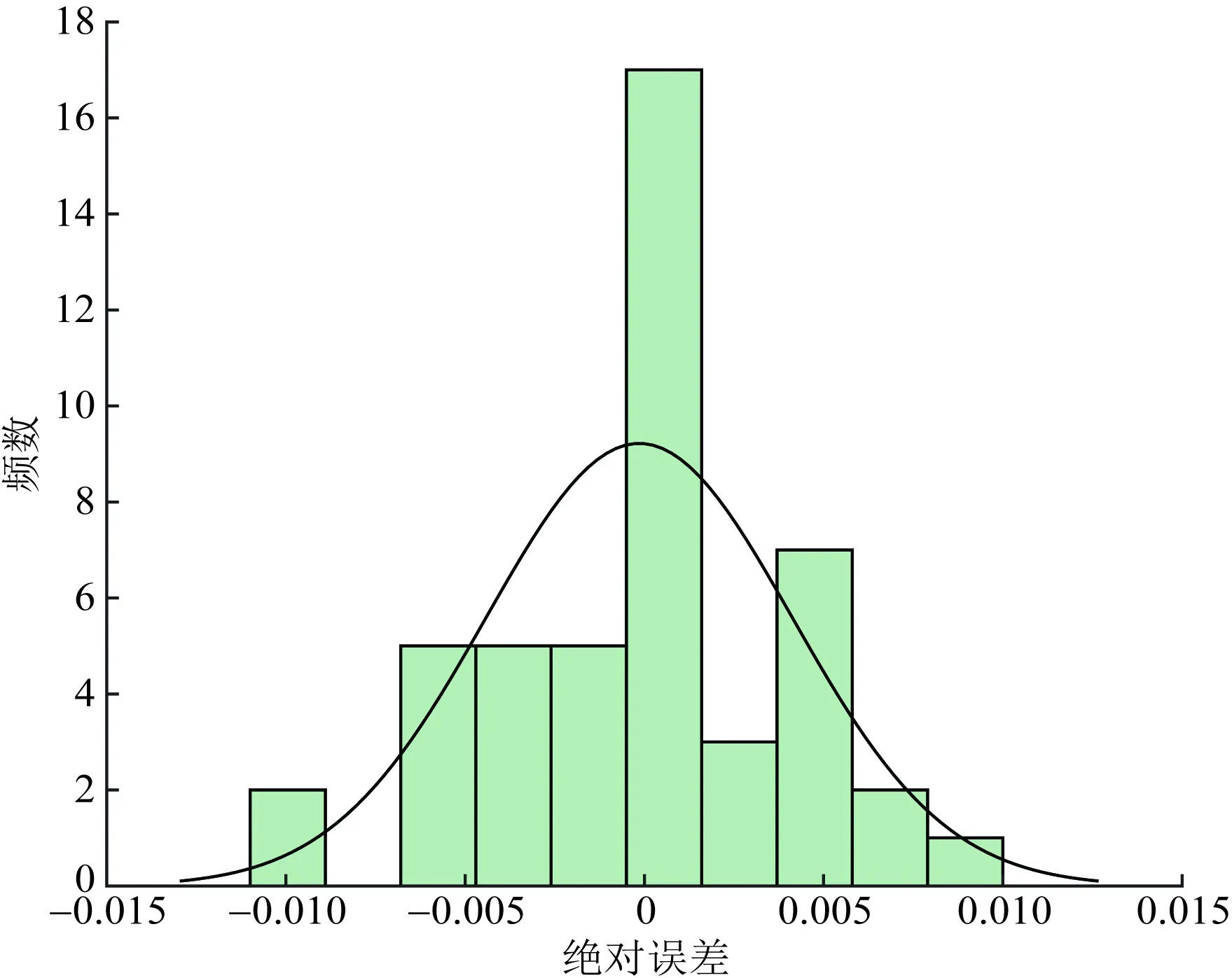
从超速率的AIC指标来看,AICZIP 3.4.2 模型参数估计分析 1)急加速、急减速率 利用Possion回归模型参数估计迭代法,急加速率、急减速率回归模型各解释变量系数估计值如表5所示。 表4 模型拟合优度指标Table 4 Model goodness of fit index 表5 急加速率、急减速率模型参数估计Table 5 Parameter estimation of rapid acceleration rate and rapid deceleration rate model (1)开口类型(x42)中,急加速率、急减速率相应的P<0.000 1,说明开口类型(x42)与急加速频率和急减速率影响均具有显著性。开口类型参数估计为正值,说明开口类型与急加速频率呈正相关性,信控开口路段发生急加速频率或急减速率可能大于无开口或右进右出开口路段。 (2)坡度、偏角的统计量在95%检验下,坡度和偏角对急加速率、急减速率的影响具有显著性。急加速率回归模型坡度的参数值为正值,急减速率相应的参数值为负值,说明坡度与急加速率呈正相关性,与急减速率呈负相关性。偏角与急加速率、急减速率均为负相关性。 (3)公交站相关统计量在95%检验下的P>0.05,因此,公交站类型对急减速频率的影响显著性不强。 (4)急加速率(y1)、急减速率(y2)与道路条件因素的关系可通过Possion回归模型描述,表达式为 y1=exp(-4.324 7+0.091 1x1-0.012x2+ 0.010 9x31+0.153 1x32+0.25x41+ 0.975 7x42) (1) y2=exp(-3.263 4-0.091 7x1-0.005 5x2- 0.141 8x31-0.003 8x32+0.118 3x41+ 0.591 9x42) (2) 2)急转弯率、超速率 由于急转弯率和超速率的统计结果中,超过60%以上的路段发生“0事件”,因此利用零膨胀回归模型拟合急转弯频率和超速频率,如表6所示。 零膨胀回归模型的参数估计分为两部分:非零值部分和零膨胀部分。非零值部分可以体现出哪些解释变量与不发生急转弯或超速行为有关,若P值小于或等于显著性,说明该解释变量对不发生异常驾驶行为有显著影响。 (1)急转弯频率回归模型中,散度系数α=0.102,聚集指数K=1/α=9.804>1,说明急转弯发生频率具有离散性。 (2)零膨胀部分。是否有公交站(x31)、公交站类型(x32)、是否有开口(x41)、开口类型(x42)这4个解释变量对不发生急转弯有显著影响;同样,公交站和开口相关解释变量对不发生超速行为有显著影响。 (3)非零值部分。坡度与急转弯频率呈负相关;偏角与急转弯频率呈正相关,偏角越大,急转弯频率越大;公交站、开口与急转弯频率呈正相关。同样,坡度、公交站与超速频率呈正相关;偏角、开口与超速频率呈负相关性。 表6 急转弯率、超速率模型参数估计Table 6 Parameter estimation of sharp turn rate and supervelocity model (4)急转弯率(y3)与多个道路条件之间的关系的零膨胀部分和非零值部分的回归模型表达式为 =-168.176-138.348x1- 4.635 48x2-222.438x31-192.807x32+ 89.743 44x41+3.594 857x42 (3) y3=exp(-5.999-0.132 45x1+0.015 237x2+ 0.282 754x31+0.188 049x32+ 0.525 225x41+0.165 674x42) (4) (5)超速率(y4)与多个道路条件的关系表达式为 =590.08+123.26x1- 9.18x2+705.99x31+567.37x32+ 341.9441-320.58x42 (5) y4=exp(-5.47+0.05x1+0.000 679x2+ 0.72x31+0.61x32-0.14x41-0.05x42) (6) 为验证回归模型拟合急加速频率、急减速频率、急转弯频率、超速频率的准确程度,随机选取与样本道路车道数、道路等级等其他条件相同的3条城市主干路,共52个路段。每天分段提取共连续6 d的过车数、急加速、急减速、急转弯、超速行为车辆数等数据,计算其异常驾驶行为率。 4.2.1 急加速率 利用急加速频率回归模型计算52个路段急加速行为频率,计算结果与实际发生急加速频率进行对比分析,急加速频率理论值与实际值对比如图5所示,急加速误差率分布如图6所示。 Possion回归模型计算的理论急加速频率与实际路段发生的急加速频率趋势大致相同。个别路段绝对误差较大,主要分布在急加速频率为0的路段,根据上述分析,急加速频率为0的路段极少,因此,对模型整体拟合程度没有影响。 根据误差率分布图,急加速频率回归模型误差率基本分布在±20%附近,所有验证路段急加速频率误差率分布在(-40%,40%)区间,且误差率大于30%或小于-30%的路段较少。 综上所述,急加速频率回归模型拟合程度较好,在一定误差范围内,能够识别路段急加速频率。 图5 急加速频率理论值与实际值对比示意图Fig.5 Comparison diagram of theoretical value and actual value of rapid acceleration frequency 图6 急加速误差率分布图Fig.6 Rapid acceleration error rate distribution 4.2.2 急减速率 利用急减速率回归模型计算的理论急减速频率与路段实际发生的急减速频率对比,急减速频率理论值与实际值对比如图7所示,急减速误差率分布如图8所示。 Possion回归模型计算的理论急减速频率与实际路段发生的急减速频率趋势大致相同(图8)。误差率分布在±20%附近的频数最大,误差率在±20%之外频数迅速下降,最大误差率在-48%左右,且误差率大于30%或小于-30%的路段极少。 急减速频率Possion回归模型拟合程度较好,在一定误差范围内,能够识别路段急加速频率。 图7 急减速频率理论值与实际值对比示意图Fig.7 Comparison diagram of theoretical value and actual value of sharp deceleration frequency 图8 急减速误差率分布图Fig.8 Rapid deceleration error rate distribution 4.2.3 急转弯率 根据拟合的急转弯频率零膨胀负二项回归模型计算验证路段急转弯频率。首先,需利用模型零膨胀部分,结合道路条件判断各分段不发生急转弯行为的概率值。若不发生急转弯行为的概率值接近1时,该分段不发生急转弯行为的概率很大,可认为该分段急转弯频率等于0。最后,根据非零值部分公式计算各分段理论急转弯频率,并将本次模型计算的理论急转弯频率与实际平均每天发生急转弯频率对比分析,急转弯频率理论值与实际值对比如图9所示,急转弯误差率分布如图10所示。 由图10可知,急转弯频率零膨胀负二项回归模型的绝对误差分布在(-0.005~0.005)的路段约占验证路段数的80.77%,且绝对误差分布在(-0.001~0)范围内的频率最大,绝对误差最大为0.01但频率较小。总体来看,急转弯绝对误差分布较好。 图9 急转弯频率理论值与实际值对比示意图Fig.9 Comparison diagram of theoretical value and actual value of sharp turn frequency 图10 急转弯频率绝对误差分布图Fig.10 Absolute error distribution of sharp turn frequency 4.2.4 超速率 同急转弯频率回归模型类似,超速频率回归模型也分为两部分:零膨胀回归模型部分、Possion回归模型部分。超速频率理论值与实际值对比如图11所示,超速误差率分布如图12所示。 由图12可知,超速频率绝对误差基本分布在(-0.002~0.002)区间,在此区间的路段数约占验证路段总数的71.15%,其中,绝对误差分布在(-0.001~0.001)区间的频数最大。总体来看,超速频率回归模型较好。 主要研究多个道路条件因素对异常驾驶行为的影响,探究山地城市道路异常驾驶行为的空间分布特征,基于Possion回归模型和零膨胀回归模型理论,建立以道路坡度、弯度、公交站和开口为因变量的异常驾驶行为率回归模型。主要结论如下。 图11 超速频率理论值与实际值对比示意图Fig.11 Comparison diagram of theoretical value and actual value of overspeed frequency 图12 超速频率绝对误差分布图Fig.12 Absolute error distribution of overspeed frequency (1)急减速行为率在不同环境下均明显大于急加速率、急转弯率和超速率,超速率均最小;在平坦、直线和信控开口路段急加速率和急减速率大于其他类型路段;急转弯行为一般发生在转弯半径较小的路段,与转弯半径关系紧密。 (2)根据模型拟合优度分析结果,急加速率、急减速率Possion回归模型拟合度较好。 (3)急转弯率、超速频率适宜用零膨胀模型。急转弯行为发生的频率具有离散性,采用ZINB形式回归模型最优;超速频率计算采用ZIP模型效果最优。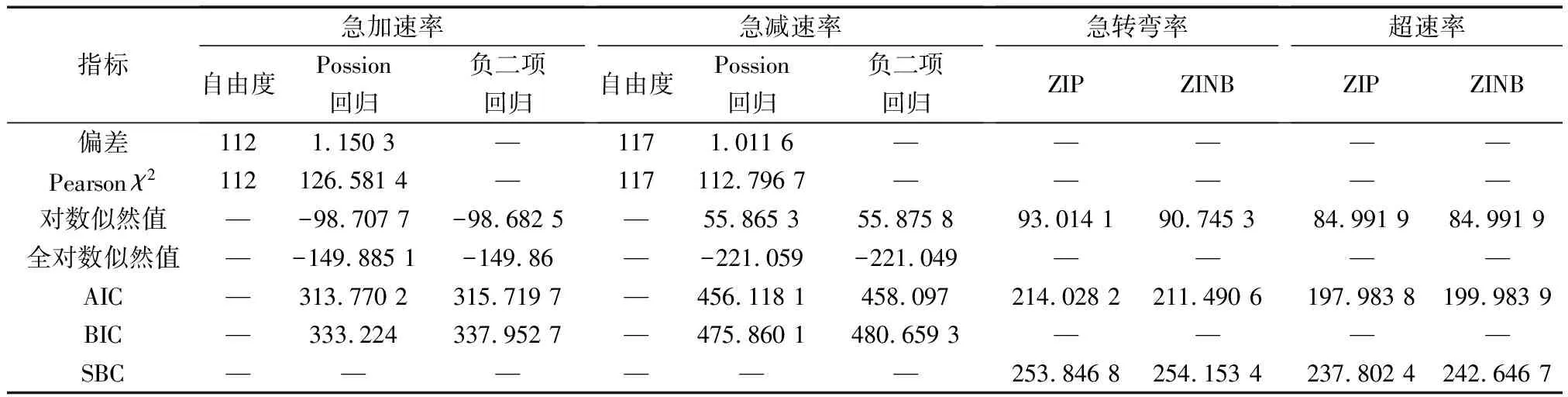


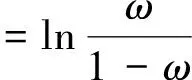
4 实例验证
4.1 实例路段选取
4.2 空间分析模型可行性验证

5 结论