能源桩热-力学特性模型试验与数值模拟

常虹， 朱万里， 王琰， 赵嵩颖

(1.吉林建筑大学测绘与勘查工程学院， 长春 130118； 2. 吉林建筑大学市政与环境工程学院， 长春 130118)

中国北方地区在冬季采暖所用的化石燃料燃烧是引起大气质量恶化的重要因素之一，利用可再生的清洁能源作为空调系统的主要能量来源是解决这一问题的有效途径。地源热泵(ground source heat pumps，GSHP)技术的基本原理是利用埋设于地下的换热管路实现建筑与地下相对恒温层的热交换，但由于其占用土地面积、钻孔造价昂贵等缺点具有一定局限性。20世纪80年代，奥地利及瑞典等国工程师提出将换热管与建筑物的混凝土桩基相结合，由此诞生能源桩的理念，又名能量桩或桩基埋管[1-2]。

由于在传统桩基础中引入温度场，能源桩运行过程中会引起桩周土温度场的变化，桩身会产生附加应力和变形，从而影响桩基承载性能。针对能源桩的研究需着重考虑如何克服循环变化的温度场对桩基力学特性的影响。近年来，针对能源桩的热-力学特性，众多学者通过试验与数值模拟等方法开展系列研究并取得一定成果。Gunawan等[3]研究不同超固结比黏土地基中能源桩的承载力特性，得出随着超固结比的增大桩顶位移逐渐减小的结论；王成龙等[4]开展室内模型试验，对饱和砂土地基中能源桩热-力耦合作用时的桩身承载力和传热机理进行研究，得出随温度循环次数的增加桩顶产生累积沉降的结论；Yavari等[5]对饱和黏土地基中能源桩力学性能进行研究，得出随着工作荷载的增大黏土蠕变速率增加，多次温度循环导致桩体产生不可逆的累积沉降的结论；郭浩然等[6]基于弹塑性理论建立能源桩数值模型，主要对能源桩运行时的受力特性进行分析，得出循环温度对桩身的影响随桩顶荷载的增大而减小的结论；黄旭等[7]开展室内模型试验，针对不封底现浇钢筋混凝土大直径管(cast-in-place concrete large-diameter pipe，PCC)能源桩运行过程中的热传导特性进行研究，得出该桩型在夏季的换热效率显著高于普通桩型的结论；Wu[8]研究了饱和黏土地基中能源桩、相邻的普通混凝土桩和承台之间的相互作用，得出邻桩和承台可限制能源桩沉降的结论；费康等[9]开展模型试验与数值模拟，对正常固结黏土地基中能源桩长期运行的热-力学特性进行研究，得出桩顶沉降随温度循环次数的增多而不断累积的结论；李小敏[10]研究了复合材料混凝土能源桩的承载力特性及传热效率，同时基于FLUENT软件开展数值模拟研究，得出铜矿渣细骨料大功率充电(high power charging，HPC)能源桩相较于传统能源桩在换热效率和承载力特性方面有显著优势；高磊等[11]采用多场耦合软件建立能源桩三维数值模型，研究螺旋形埋管能源桩的热-力学特性，得出桩身应变随桩长缩短而线性减小等结论；杨涛等[12]采用数值模拟方法对热-力耦合作用下的能源桩承载力特性进行研究，设置温度荷载按正弦函数变化，得出桩周土相较于桩身温度变化较为滞后等结论；史宏财等[13]基于圆柱源换热理论建立非饱和土地基中能源桩数值模型，提出桩周土饱和度与能源桩换热比率的函数关系，并开展室内试验验证了模型适用性；赵蕾等[14]基于COMSOL软件建立不同埋管形式能源桩的数值模型，对比研究其换热性能、轴力、桩身位移等方面的不同，得出双螺旋形埋管的能源桩换热效率较高、W形埋管能源桩的桩身附加温度荷载较大的结论。

越来越多的学者将数值模拟方法运用到能源桩研究领域，运用有限元数值模拟软件计算得出的结果可以一定程度上与试验结果相互印证。近年来，针对能源桩热-力学特性的研究主要集中于砂土和非饱和黏性土地基，而针对饱和黏土地基开展的研究相对较少。鉴于饱和黏土具有高含水量、低强度、高压缩性、低渗透性等特点，且温度改变引起的饱和黏土变形会改变桩土的位移模式，进而改变桩侧阻力和端阻力的发挥，现结合室内模型试验与数值模拟，展开饱和黏土地基能源桩在冷热交替循环过程中的力学特性研究，为能源桩在饱和黏土地基的应用给出建议。

1 试验设计

1.1 试验系统

饱和黏土地基中能源桩模型试验系统包括模型槽、量测系统、换热系统和加载设备。模型槽是由聚甲基丙烯酸甲酯板材围成的直径550 mm的圆桶，该材料具有延展性好、抗冲击力强等特点。紧贴模型槽内壁覆有透明塑料薄膜，以防止内部土体水分流失。基准梁横跨模型槽两侧，用以固定数显百分表，测量桩顶位移。假定基准梁与大地变形协调，不考虑基准梁形变对数据的影响。量测系统包括DH3818静态应变测试系统、120-50AA混凝土应变片(量程0～20 000 με，1/4桥式)、电阻式微型土压力盒、PT100铂热电阻温度传感器、温度采集仪、数显式百分表(精度0.01 mm)等。应变片和土压力盒与DH3818相连，温度传感器与温度采集仪相连，可自定义采集频率，数据自动采集。换热系统由数显恒温水浴锅及全自动自吸水泵组成，导热液体为水，循环流速为22 L/min。加载设备为铁制砝码，工作荷载与桩顶之间垫有刚性加载板。

1.2 桩周土体参数

试验用土为饱和黏土，其物理力学参数如表1所示。

表1 饱和黏土物理性质Table 1 The physical properties of saturated clay

1.3 模型桩制作

试验所用模型桩采用C30强度的混凝土浇筑，模型桩直径D=84 mm，桩长L=500 mm，主筋由3根HRB400C8 mm钢筋组成，箍筋为B6 mm@100 mm。桩内换热水管为PVC钢丝软管，水管外径为14 mm，内径8 mm，试验采用单U形埋管方式，U形两肢相距32 mm。

1.4 试验方案

1.4.1 准备工作

试验采用亚克力板围成的直径550 mm的模型槽，槽内土体高度H=500 mm，分3层填筑，每层虚高20 cm，并以18 kPa荷载静压48 h再进行下一层填筑，每填筑一层适当对土体喷水养护以保证土体始终处于饱和状态。桩端持力层填筑完成后，在桩底位置埋设土压力盒。土体填筑结束后，将模型地基静压一周，以形成正常固结状态的饱和黏土地基。

量测系统包含的各传感器布设如图1所示，桩顶对称布置两个百分表B1、B2以测定桩顶竖向位移，读数取二者平均值；在距离土体表面5、200、400 mm深度分别布置3层、每层布置4个共计12个温度传感器(T1～T12)，同一深度处传感器分别距桩轴线42 mm(1/2D)、84 mm(1D)、168 mm(2D)、252 mm(3D)；土体表面距桩侧30、130、230 mm处分别布设3个百分表B3、B4、B5，以测定土体沉降；土压力盒布置在桩端下，距离模型槽底部10 cm，以测量桩端阻力；在桩身两侧对称粘贴应变片，每侧4片等距布置，共计8片。

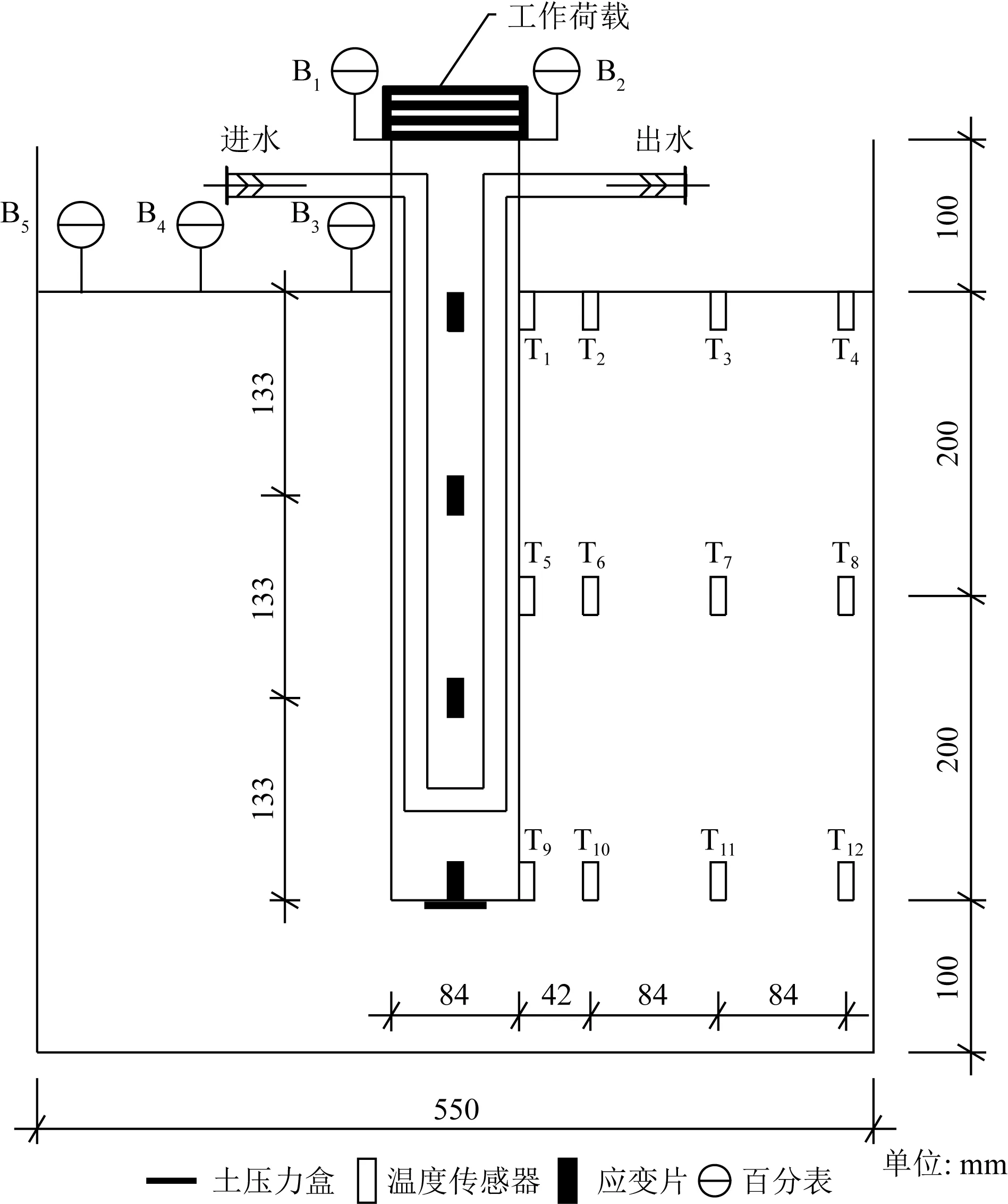
图1 测点布置图Fig.1 Layout of measuring points

1.4.2 能源桩静载荷试验

首先按照规范估算模型桩的极限承载力，随后按照计算所得的极限承载力分10级加载。静载试验采用慢速维持荷载法，加载过程中记录桩顶沉降，当每级荷载下桩顶沉降量小于0.1 mm/h时，则认为已趋于稳定，可施加下一级荷载。当某级荷载下桩顶沉降量为前一级荷载下沉降量的5倍，则立即终止加载。根据《建筑基桩检测技术规范》(JGJ 106—2014)[15]的规定，荷载-沉降曲线上出现陡降段时，单桩极限承载力取陡降段起点的荷载值为1.0 kN，取工作荷载为0.5 kN。

1.4.3 试验工况

根据温度荷载大小、循环次数及桩顶荷载情况将试验分为5种工况，具体见表2。

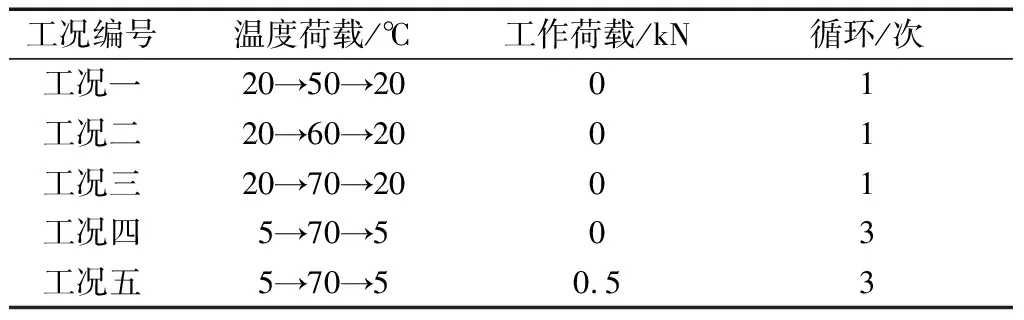
表2 试验工况Table 2 Test conditions

设定工况一～工况三初始温度为20 ℃以模拟室温，3种工况下分别将换热液体加热至50、60、70 ℃，升温过程约为15 min，达到目标温度后维持24 h，随后将循环液体迅速冷却至初始温度并维持5 h。工况四和工况五将温度循环设定为5 ℃→70 ℃→5 ℃，升温过程约为30 min，达到70 ℃后维持24 h，随后将循环液体迅速冷却至5 ℃并维持5 h，如此循环3次。

2 试验结果分析

2.1 桩身和土体温度变化规律

在数据处理时发现T1测点的热响应较迅速，故选取工况一～工况三的T1测点数据，分析循环水温度的高低对桩身温度的影响，从图2可以看出，初始阶段桩身温度升高较明显，超过5 h后逐渐趋于稳定，3种工况下桩身最高温度分别为30.0、34.8、38.5 ℃，可知桩身温度随入水温度的升高而升高。

图3为工况四所得温度随时间变化曲线，可以看出，桩身各点温度在初始阶段升温较快，超过5 h后逐渐趋于稳定，测点T1、T5、T9的最高温度分别为38.8、35.1、25.6 ℃，沿深度方向桩身温度逐渐减小，随循环次数的增加，桩身最高温度先降低后升高，考虑是桩周土体温度改变较为滞后，桩-土换热量先增加后减小的缘故。

图4为距离填土表面200 mm深度处土体沿径向的温度变化，可以看出，距离桩越远土体温度越低，远端T8点的温度变化不明显；随循环次数的增加，土体温度曲线逐渐变缓，温度逐渐降低。

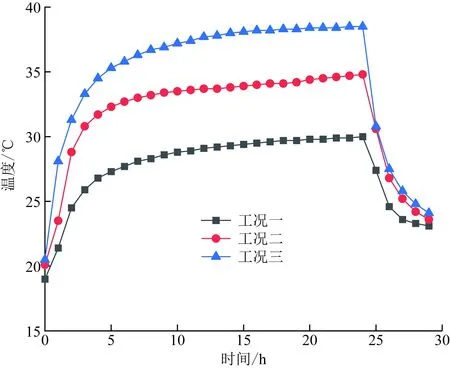
图2 不同循环温度下桩身温度变化曲线Fig.2 The change curves of pile temperature at different temperature cycles

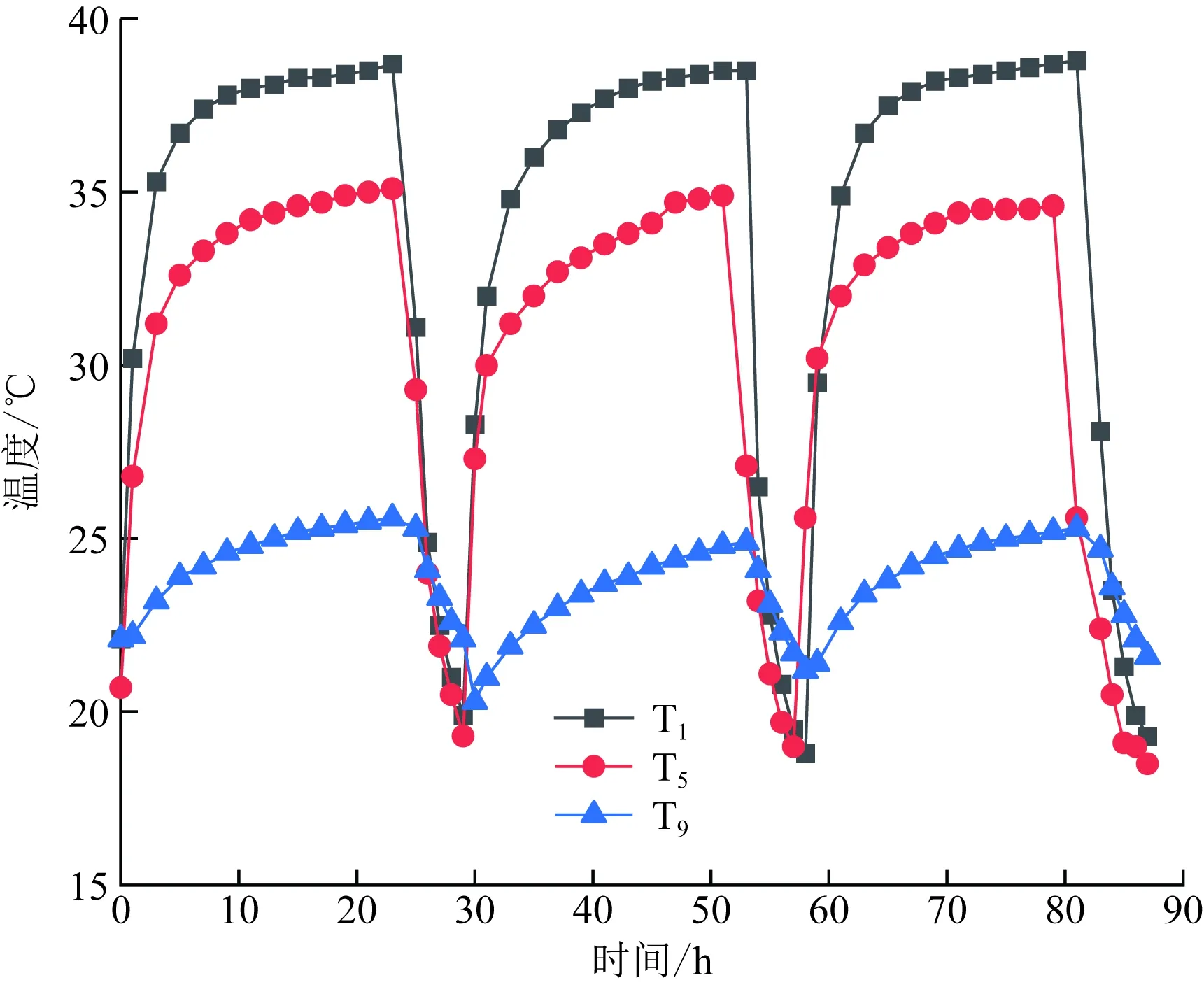
图3 工况四桩身温度随时间变化曲线Fig.3 The change curves of pile temperature with time in the fourth condition

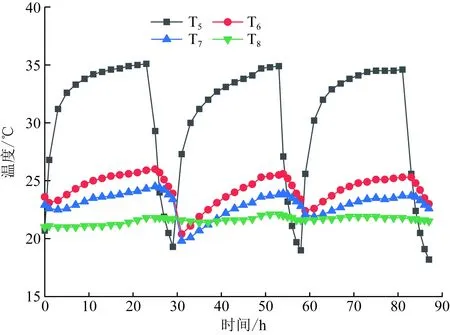
图4 工况四土体温度随时间变化曲线Fig.4 The change curves of soil temperature with time in the fourth condition

2.2 桩顶和土体位移

2.2.1 桩顶位移

工况四多次温度循环下桩顶沉降变化如图5所示，规定向上的位移为正，向下的位移为负，可以看出，升温阶段桩体发生膨胀，桩顶产生向上的位移，最大上升位移为0.089 mm；降温时桩体收缩位移向下，最大沉降为0.052 mm，降温所导致的沉降量大于升温的膨胀量，考虑到桩端黏土由于桩体膨胀产生变形所致，随着循环次数的增加，桩体的不可恢复沉降将逐渐累积，三次温度循环后桩顶产生累积沉降量达-0.052 mm(0.6%D)，此结论与王成龙等[4]、Yavari等[5]、Liao等[16]的结论一致，工程上须保证能源桩长期运行的稳定性，而桩顶位移尤其是沉降位移是影响结构安全的重要因素，尤其对于饱和黏土地基多次温度循环后的桩顶累积沉降应引起足够重视。

2.2.2 土体位移

选取工况四土体表面竖向位移数据绘制位移-时间曲线，如图6所示。百分表B3靠近桩身，由于升温阶段桩体膨胀产生挤土效应，土体表面隆起，故表现为较大的上升位移，不予考虑。升温阶段，由于土体发生热固结现象产生沉降；降温会加剧土体沉降，考虑是由于超静孔隙水压力的消散使土体固结程度增大的缘故[17]。受土体温度场的影响，靠近桩身土体的沉降速率大于远端。随循环次数的增加，土体沉降速率呈减小趋势，三次温度循环后，B4、B5处土体的最终沉降量分别为-1.19 mm和-0.61 mm。因此，能源桩应用于饱和黏土地基时，设计阶段需考虑到黏土发生热固结现象，产生收缩变形对桩基承载力的影响。

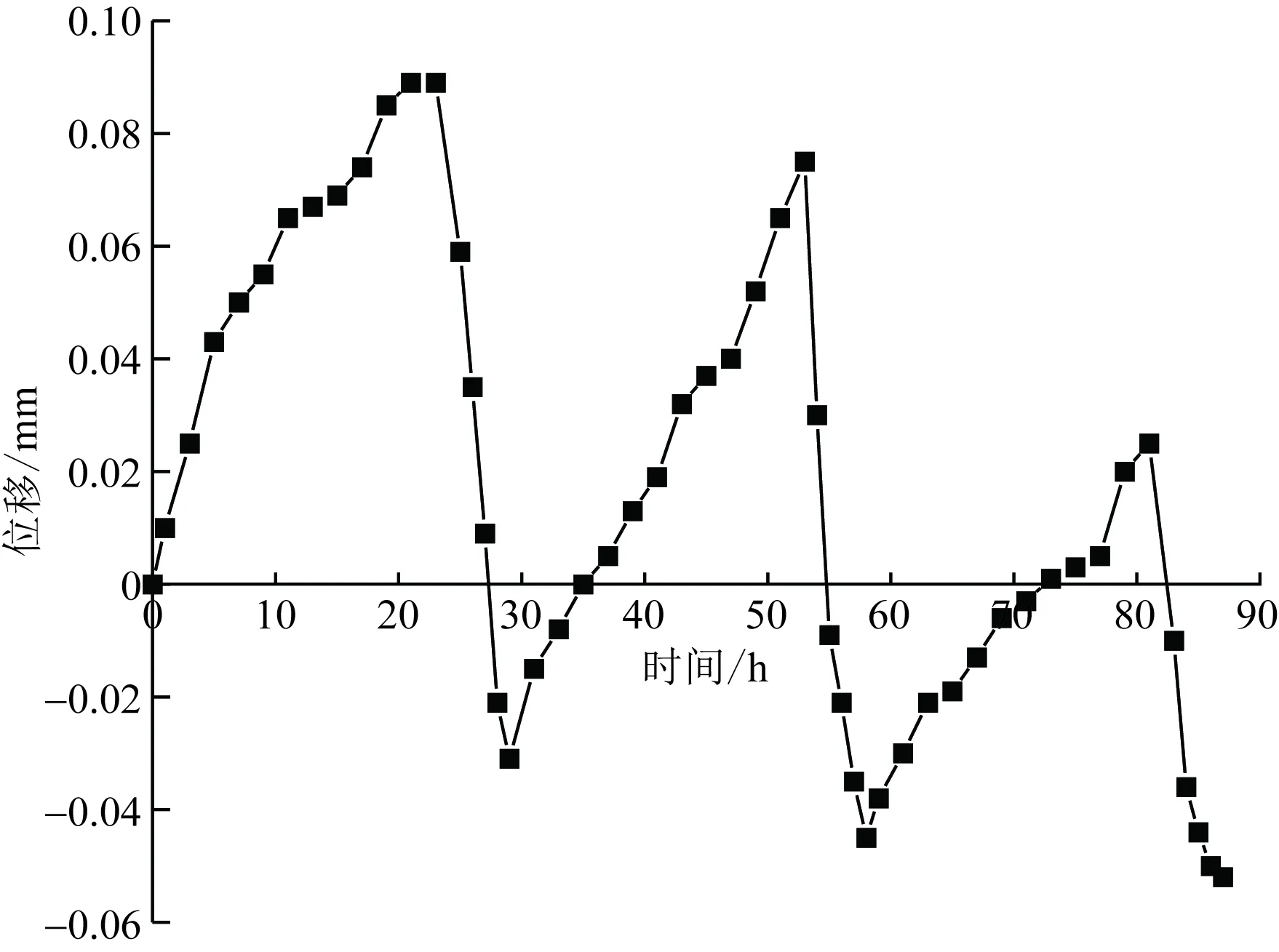
图5 桩顶位移变化曲线Fig.5 The curve of displacement of pile top

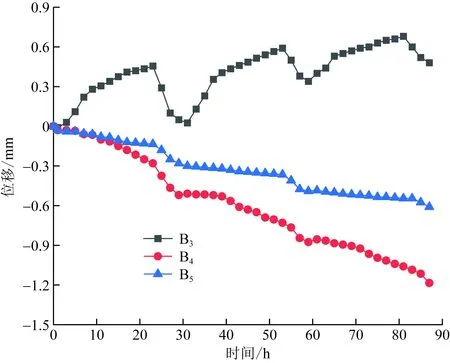
图6 土体表面竖向位移变化曲线Fig.6 The curves of vertical displacement of soil surface

3 试验与模拟力学特性对比分析

3.1 三维数值模型建立

基于COMSOL Multiphysics软件建立与能源桩试验装置等大的三维数值模型，利用软件内置的岩土工程模块和偏微分方程(partial differential equation，PDE)引入物理力学场和温度场，为优化求解过程，在建立模型之初做出如下假设：①默认桩周土壤中无地下水渗流运动；②桩身及桩周土材料的物理力学参数保持恒定，不随温度场而变化；③将换热管及换热液体简化为线性热源；④数值模型的初始温度统一且均匀分布。

考虑到计算难度随网格划分细密程度线性增长，对换热管采用边单元网格划分法，最小单元尺寸0.12 mm，桩身及桩周土体采用自由四面体网格划分法，最小单元尺寸分别为0.9 mm和2.4 mm，如图7所示。

桩身应力测点分布越密集，越利于分析桩身力学性质，在数值模拟中沿桩身等距取9个测点，相邻测点间距为50 mm，运用COMSOL软件内置的岩土工程模块计算桩身各项力学指标。

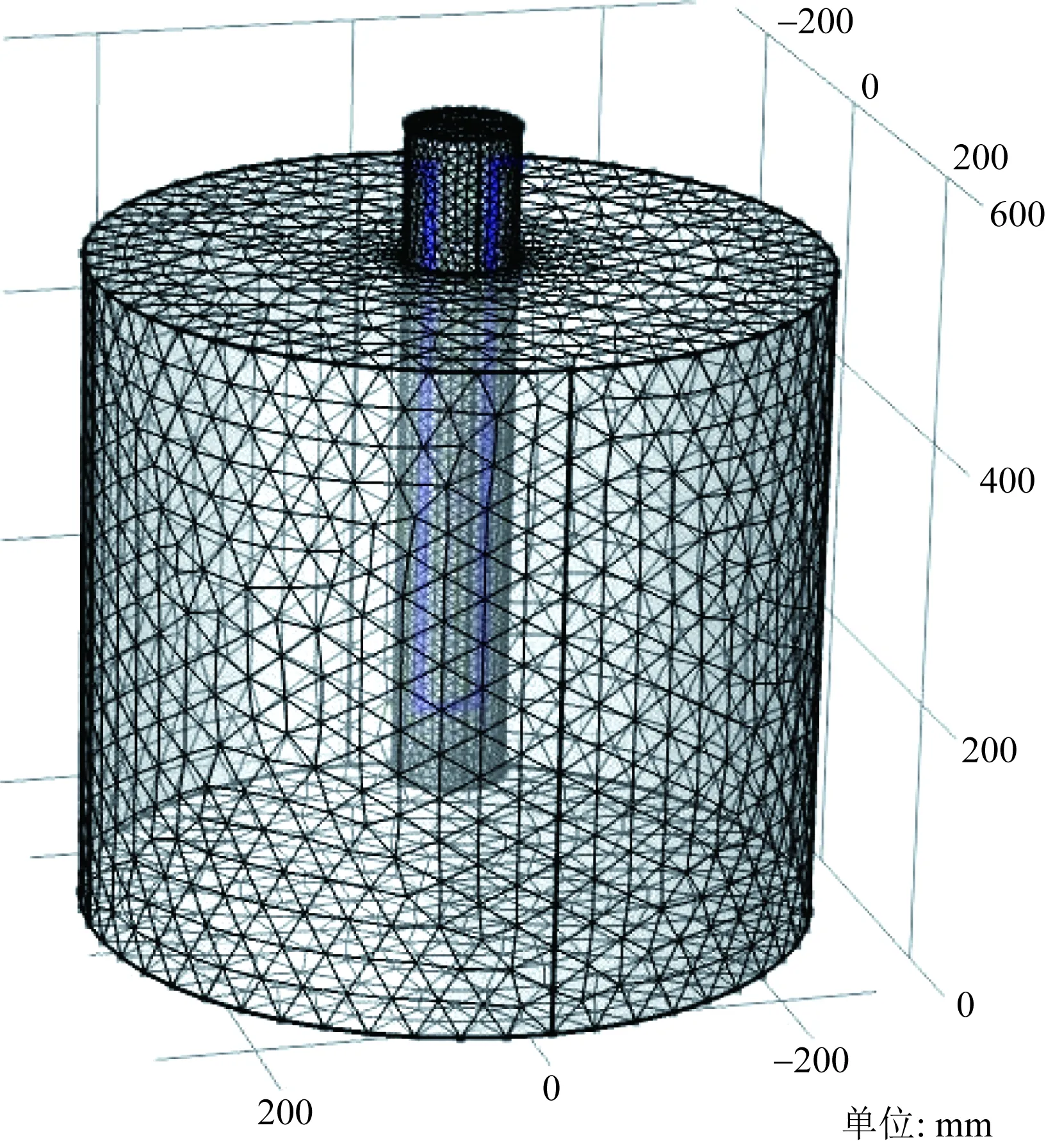
图7 模型网格划分Fig.7 Model meshing

3.2 桩端土压力

桩端阻力的变化表现为桩端土压力的变化，5种工况下桩端土压力随时间变化的曲线如图8所示。加热和制冷阶段开始后，各工况下桩体的桩端土压力在2 h内分别迅速增加和减小，考虑是由于桩体温度未达到稳定状态，2 h之后桩端土压力逐渐趋于稳定。由于循环温度的差别，桩端土压力的大小也各不相同。

工况一～工况三加热阶段结束后，桩端出现的最大压应力分别为0.064 1、0.086 1、0.109 5 MPa；制冷结束后，桩端最小压应力分别为0.017 6、0.020 6、0.021 8 MPa。加热后桩体受热膨胀，桩端土压力升高，而制冷时桩体受冷收缩，桩端土压力逐渐减少，这与 Yavari 等[5]的结论基本一致。循环水的温度越高，桩端土压力越大；加热与制冷阶段的温差越大，桩端最大压应力与最小压应力的差值越大。由工况四和工况五的土压力变化曲线可以看出，工作荷载作用下，加热结束时的桩端压应力约为零荷载作用下的1.65倍，制冷结束时的桩端压应力约为零荷载作用下的14倍，变化规律与王成龙等[4]基本一致。加热阶段结束后，桩端出现的最大压应力分别为0.107 6 MPa和0.178 4 MPa；制冷结束后，桩端最小压应力分别为0.005 9 MPa和0.084 4 MPa。随循环次数的增加，桩端最大压应力逐渐减小，考虑是由于桩周土体在多次冷热交替后发生热固结作用，土体强度增大的缘故。

数值模拟所得桩端土压力随能源桩运行时间的变化趋势与试验结果基本一致，数值相对较大。数值模拟桩端土压力平均值相较于试验结果偏大20%～25%，考虑是由于建立模型时简化荷载传递公式的缘故。

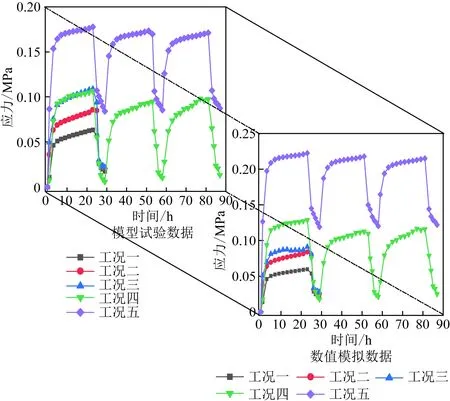
图8 试验与模拟桩端土压力对比图Fig.8 Comparison of pile end earth pressure between test and simulation

3.3 桩身侧摩阻力分布规律

温度循环引起的桩体膨胀和收缩受到约束时，在桩体内部会产生轴向附加应力，此时桩身实际热应变小于自由应变εT-free，产生热应力σT，进而引起桩侧摩阻力的改变，不同深度处的桩侧摩阻力fs,mob,j计算公式推导过程如下。

εT-free=αcΔT

(1)

σT=EεT-rstr=E(εT-free-εT-obs)

(2)

fs,mob,j=(σT,j-σT,j-1)D/(4Δl)

(3)

式中：σT为温度荷载下桩身的附加热应力，MPa；E为弹性模量，GPa；εT-rstr为温度荷载下桩身的附加热应变；εT-free为温度荷载下桩身的自由应变；εT-obs为温度荷载下桩身的观测应变；αc为桩体热膨胀系数，桩体热膨胀系数采用 10 με/℃；ΔT为测点温差，℃；D为桩体直径；Δl为相邻应变片的间距；j=1,2,3,4表示从土表面到桩端应变片编号。定义侧摩阻力向上为正，向下为负。

工况一～工况三中24 h和29 h的桩身侧摩阻力-深度分布曲线如图9所示。对比分析模型试验数据与数值模拟数据可发现二者侧摩阻力趋势基本一致，桩体受热时两端分别向上和向下运动，桩体上半部分产生负的侧摩阻力，下半部分产生正的侧摩阻力；桩身侧摩阻力随循环温度的升高而逐渐增大；无论升温阶段还是降温阶段，位移零点均产生在桩身中部偏下位置；桩端附近产生的侧摩阻力数值均小于桩体上半部分侧摩阻力数值，考虑因为桩端土的约束作用使桩-土相对位移较小的缘故。

取工况四和工况五24 h和29 h的桩体侧摩阻力进行对比，以此分析工作荷载作用对侧摩阻力的影响，试验与模拟结果对比如图10所示。桩体升温时，桩体上部侧摩阻力为负，下部侧摩阻力为正，降温时恰好相反。模型试验升温结束时，零荷载和工作荷载作用下最大侧摩阻力值分别为0.062 1 MPa和0.046 0 MPa；29 h时刻，二者最大侧摩阻力值分别为0.029 9 MPa和0.047 3 MPa。工作荷载作用使桩身整体下沉，产生负摩阻力的区域逐渐变小，相较于零荷载作用时，位移零点上移至桩中部偏上位置，此结论与数值模拟结果一致。

选取工况五升温和降温结束时的桩侧摩阻力数据绘制其沿深度分布图，以分析温度循环次数对桩体侧摩阻力的影响，如图11所示。可以看出，无论升温或降温阶段，靠近土体表面处的模拟结果均明显小于试验结果，考虑是由于两处位于温度场的边缘，温度变化幅度较小且迟缓，不会产生明显的热量堆积效应，桩身附加热应力相对较小的缘故。因此，在设计模型试验时需注意在桩身两端细分应力测点。模型试验与数值模拟的桩身中下部侧摩阻力值无较大差异，试验与模拟结果的最大侧摩阻力值基本相同。模型试验中3次循环升温阶段的最大侧摩阻力值依次为0.046 0、0.049 1、0.050 6 MPa；降温时最大侧摩阻力值依次为0.047 3、0.052 3、0.052 9 MPa。多次温度循环后，降温时位移零点下移至桩体中部偏下位置，升温阶段位移零点的位置始终保持在桩体上部。随着循环次数的增加，侧摩阻力逐渐增大，增量逐渐减小，考虑是多次冷、热循环使桩侧土体产生固结变形对桩体的约束作用增强的缘故。

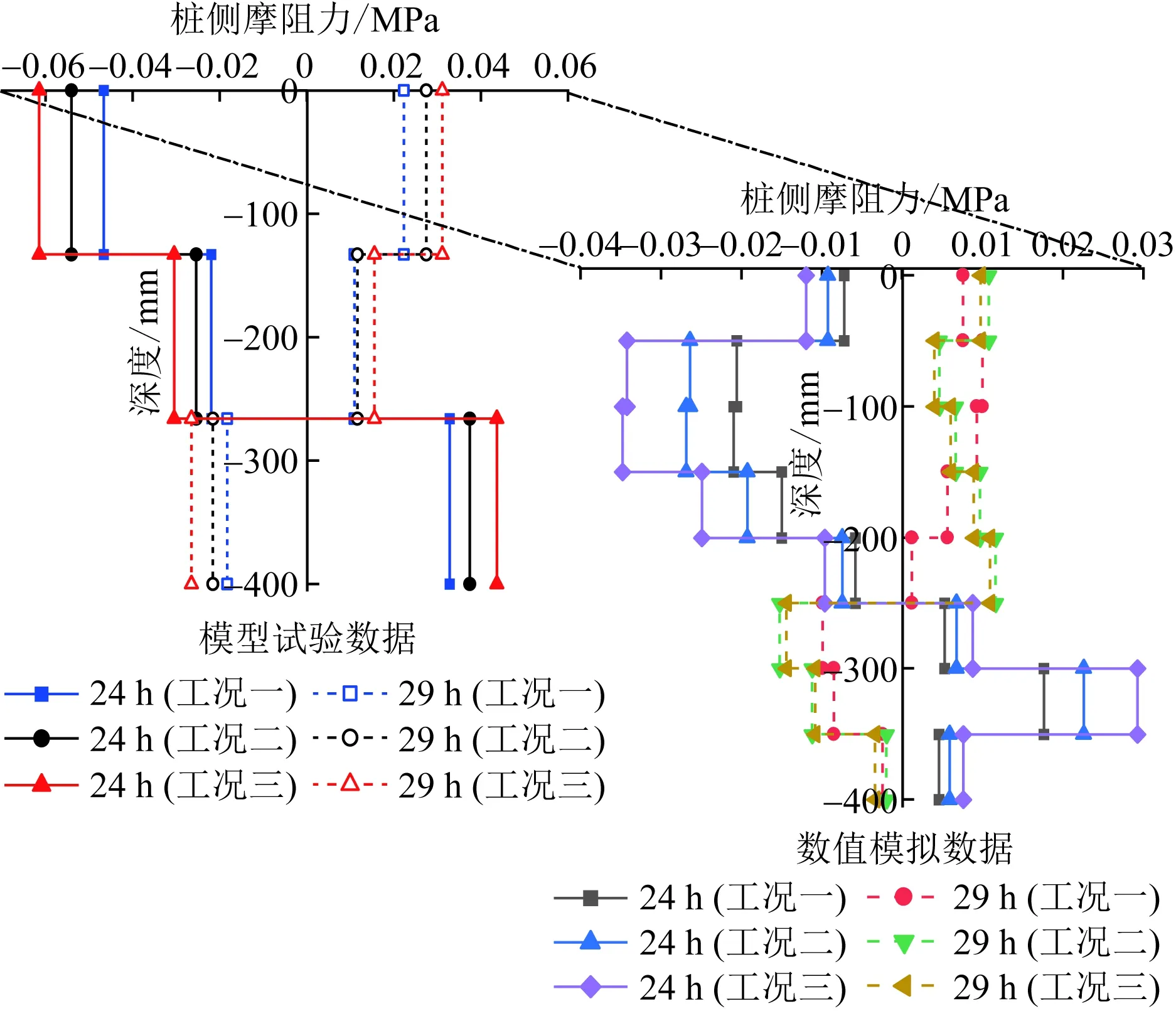
图9 工况一～工况三侧摩阻力沿深度分布Fig.9 The shaft friction distribution along depth in the first to third conditions

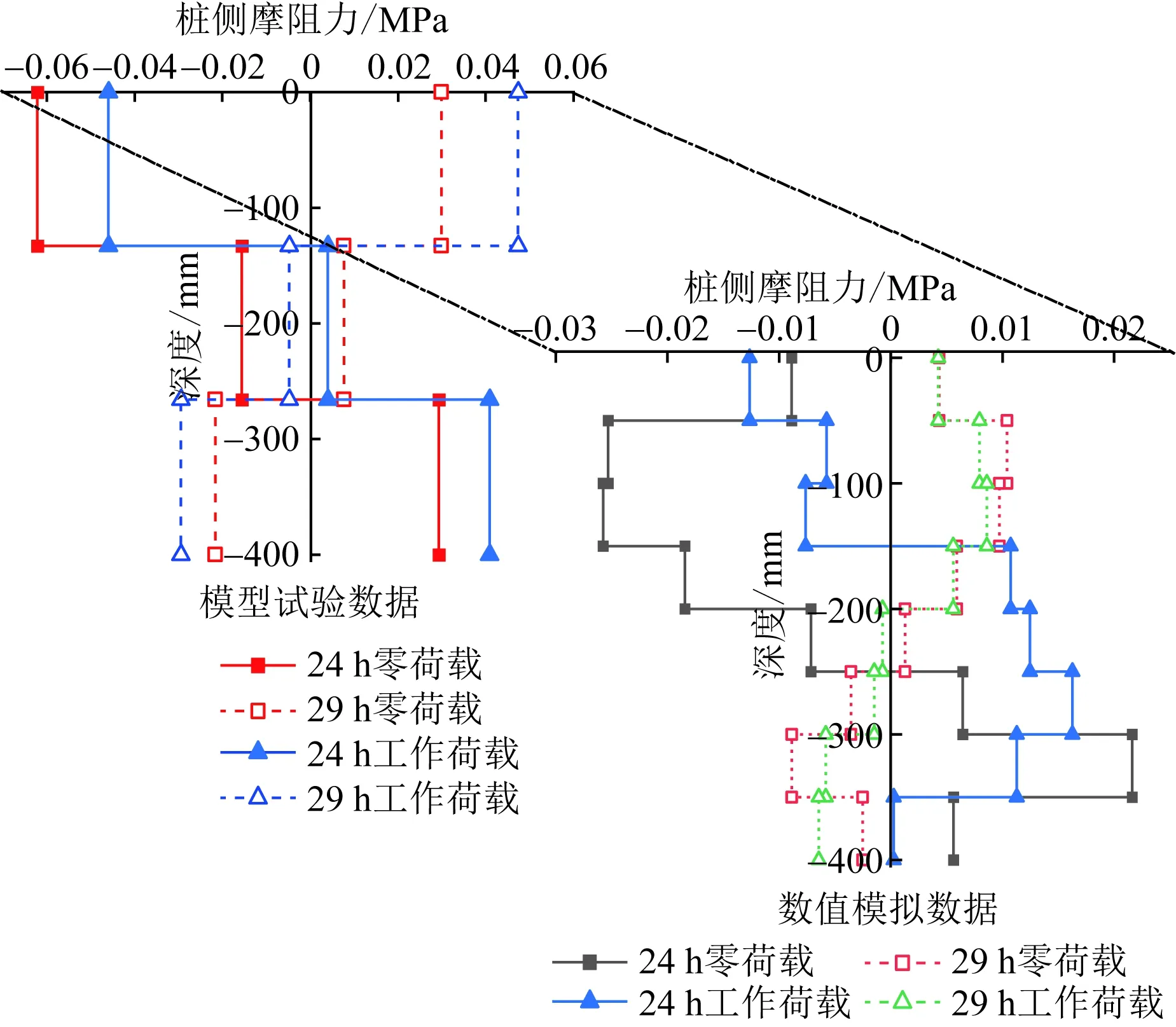
图10 工况四、工况五侧摩阻力沿深度分布Fig.10 The shaft friction distribution along depth in the fourth and fifth conditions

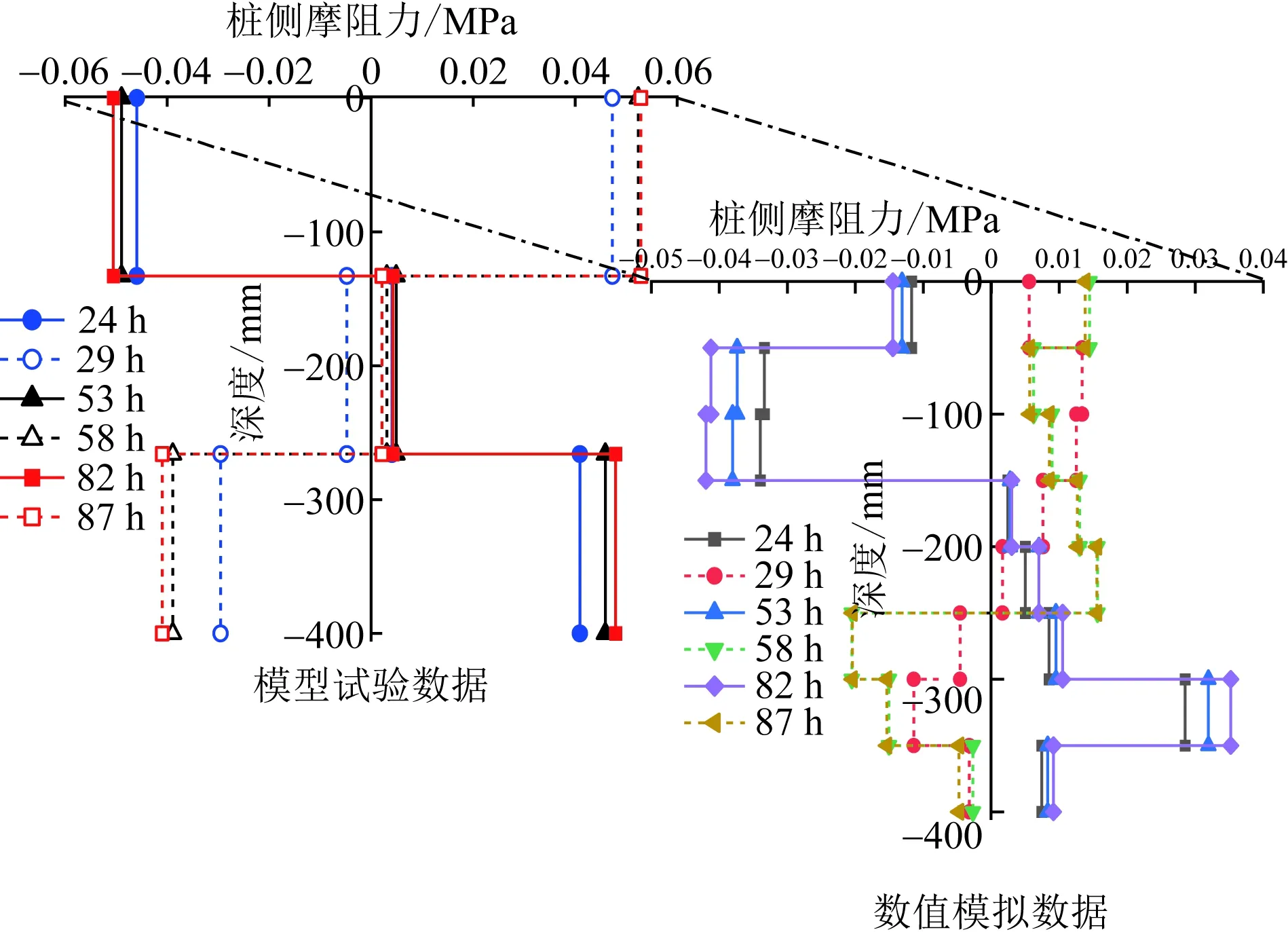
图11 工况五试验与模拟侧摩阻力对比图Fig.11 The shaft friction distribution of test and simulation in the fifth condition

4 结论

通过开展不同工况下饱和黏土地基中能源桩室内模型试验和数值模拟研究，将模拟结果与试验结果相互印证，获得桩土温度、位移和桩基承载力及其变化规律，得到如下结论。

(1)对换热液体加热时，前5 h桩身温度迅速升高，随后逐渐趋于稳定。降温阶段所引起的桩顶沉降量大于升温产生的膨胀量，且多次温度循环导致的累积变形可能会对上部建筑的安全造成影响，在设计阶段需引起重视。多次温度循环使土体发生热固结现象，桩周土体表现为沉降，靠近桩身土体的沉降速率大于远端。随循环次数的增加，桩周土体的沉降速率呈减小趋势。

(2)桩身侧摩阻力随温度的升高而逐渐增大，任一工况桩端附近产生的侧摩阻力数值均小于桩顶部分的侧摩阻力数值，且侧摩阻力随循环次数的增加而逐渐增大。工作荷载的加入导致桩身产生负摩阻力的区域逐渐变小，位移零点逐渐上移。

(3)采用数值模拟研究方法可以较好地模拟能源桩温度循环下的承载力特性，数值模拟结果可与模型试验结果做到相互印证。数值模拟所得的侧摩阻力在靠近土体表面处和桩端处明显小于模型试验后果，在设计试验时需注意增加在桩身两端的测点以便于更完整、细致地分析能源桩侧摩阻力趋势。