钢管混凝土抛物线空腹拱平面内稳定性能

陈立旗， 袁波*

(1.贵州大学空间结构研究中心， 贵阳 550025； 2.贵州省结构工程重点实验室， 贵阳 550025)

拱结构作为轴向受压构件[1]被广泛使用在桥梁工程中。因此，在拱桥中应用具有高抗压强度的钢管混凝土可以显著提高其承载能力[2]。此外，这种结构在施工时可以先架设质量轻的钢管跨越山谷或者河流，然后在架设好的钢管内灌注混凝土，此时钢管可以作为混凝土的模板。这种施工工艺不仅避免了复杂的施工方法，而且提高了施工速度，增强了拱结构的跨越能力[3]。

随着钢管混凝土拱桥在实际生活中被广泛使用，其平面内的稳定性能越来越受到关注。中国于2013年颁布的《钢管混凝土拱桥技术规范》[4]采用等效柱法来计算钢管混凝土拱的平面内稳定承载能力，即将钢管混凝土拱简化为钢管混凝土柱，并将其作为轴心或偏心受力构件进行计算。然而，与钢管混凝土柱相比，钢管混凝土拱的稳定性不仅取决于长细比，还取决于矢跨比，尤其矢跨比小于0.2的浅拱[5]。此外，在实际生活中，除了承受轴向力之外，钢管混凝土抛物线拱还可能承受分布不均匀的弯矩，从而使其成为压弯构件。现行规范[4]中将钢管混凝土拱作为偏心受力构件[6](即均匀弯矩分布)设计从而忽略了分布不均匀的弯矩对其极限承载力的影响[7]。

目前，国内的许多学者对钢管混凝土拱的平面内稳定性能进行了大量研究。李晓倩[8]基于2011年福建省颁发的《钢管混凝土拱桥技术规程》(DBJ/T13-136—2011)，对钢管混凝土抛物线圆管拱的平面内稳定性能进行研究，提出抛物线拱的稳定公式。韦建刚等[9-10]在等效梁柱法的基础上，提出考虑矢跨比和初始缺陷的修正公式。Wu等[5]和Liu等[11]以美国钢结构协会推荐的稳定公式为基础，进行参数化分析，提出钢管混凝土圆管拱的轴压和压弯设计公式。殷海棠等[12-13]在试验的基础上，对钢管混凝土抛物线圆管拱的稳定公式进行对比总结，提出跨中加载和半跨多点加载的空间压弯稳定公式。

根据陈宝春等[14]对已建钢管混凝土拱桥参数的统计分析，发现截面上以单圆形、哑铃型和桁式在工程上应用是主流。但在实际工程中，发现有一种在钢管混凝土桁架拱[15]的结构形式上取消斜腹杆的拱结构(本文中称为钢管混凝土空腹拱)，如纬七路湖滨大桥。而钢管混凝土空腹拱在规范[4]中设计方法不完善，具有研究价值。

为研究钢管混凝土空腹拱的平面内弹塑性屈曲性能，现通过施加不同的荷载工况，提出考虑轴力和弯矩的共同作用下钢管混凝土抛物线空腹拱的平面内稳定承载力公式。

1 结构形式及有限元建模

1.1 结构形式及选用参数

钢管混凝土空腹拱采用钢管，按照一定间隔连接上下两根钢管混凝土而成，且腹杆的轴线垂直于拱轴线。其结构形式如图1所示。

L为拱的跨度； f为拱的矢高；S为拱轴线弧长；Lc为节段长度； D为弦杆的直径；t为弦杆的壁厚；d为腹杆的直径；t0为腹杆的 壁厚；H为截面的高度图1 拱的结构形式Fig.1 Structural form of arch

1.2 建立有限元模型

1.2.1 选择单元类型及边界条件

在建模过程中，为了考虑剪切变形的影响，拱肋和腹杆均采用B31型Timoshenko梁单元。在模拟钢管混凝土截面时，拱肋采用采用双单元建立组合截面[16]，即在两个节点之间建立两根梁单元，一根梁赋予钢管的截面属性和材料，另外一根梁赋予混凝土的截面属性和材料。采用双单元建立截面后，可以使两者的变形协调，不考虑滑移的影响。为了快速实现双单元截面的建模，采用Python语言修改inp文件完成。

1.2.2 选择材料本构

在进行有限元软件建模时，钢管的本构关系采用韩林海[17]提出的五段式模型，即弹性阶段(oa)、弹塑性阶段(ab)、塑性阶段(bc)、强化阶段(cd)和二次塑流阶段(de)。而混凝土的本构关系采用韩林海[17]提出的核心混凝土非线性应力应变模型，该模型充分考虑约束效应系数ξ的影响。

1.2.3 初始缺陷的引入

初始缺陷分为几何初始缺陷和材料初始缺陷。几何初始缺陷对钢管混凝土结构的承载能力具有明显影响[18-19]。建模中采用一致缺陷法来模拟几何初始缺陷对承载能力的影响，且初始缺陷幅值为S/1 000(S为拱轴线长度)。材料初始缺陷是指由于构件在制造过程中在内部产生的自应力，如钢管在焊接时由温度产生的应力。在进行钢管混凝土圆弧拱平面内稳定性能研究时，发现温度产生的应力对拱肋的稳定性能影响不大[3]，故暂不考虑材料初始缺陷的影响。

1.2.4 有限元模型及荷载工况

采用ABAQUS建立钢管混凝土空腹拱模型，如图2所示。在有限元的基础上，对拱施加全跨均布荷载、半跨均布荷载以及跨中集中荷载，其中q为均布荷载，P为集中荷载，如图3所示，研究其在这几种荷载下的稳定性。

图2 拱的有限元模型Fig.2 Finiteelement model of arch

图3 荷载工况Fig.3 Load case

1.3 实验验证

钢管混凝土空腹拱是采用钢管连接两根钢管混凝土单圆拱而成的拱结构，因此只要验证钢管混凝土单圆拱的正确性。Liu等[11]在哈尔滨工业大学结构实验室进行了钢管混凝土抛物线圆管拱的面内稳定试验，其中模型的拱肋跨度为9 m，钢管截面尺寸为159 mm×4.5 mm，选用矢跨比为1/6来研究其面内承载能力。由图4可知，试验得到的拱的稳定承载力荷载与有限元模拟出来的稳定承载力吻合度较好，两者最大相差为8.33%。因此，采用本文提及的建模思路，能正确模拟钢管混凝土空腹拱的稳定性。

图4 有限元与试验结果对比Fig.4 Comparison between finite element and test results

2 换算长细比

刘昌永[14]推导过钢管混凝土抛物线桁架拱的换算长细比。在钢管混凝土抛物线空腹钢中，由于没有斜腹杆，其在剪力作用下的机理应按照缀板式轴心受压柱的剪力刚度计算方法去计算。在每一个节段间，由于当节段Lc较小，所以近似将节段视为直线段，其在单位剪力作用下的弯矩图如图5所示。

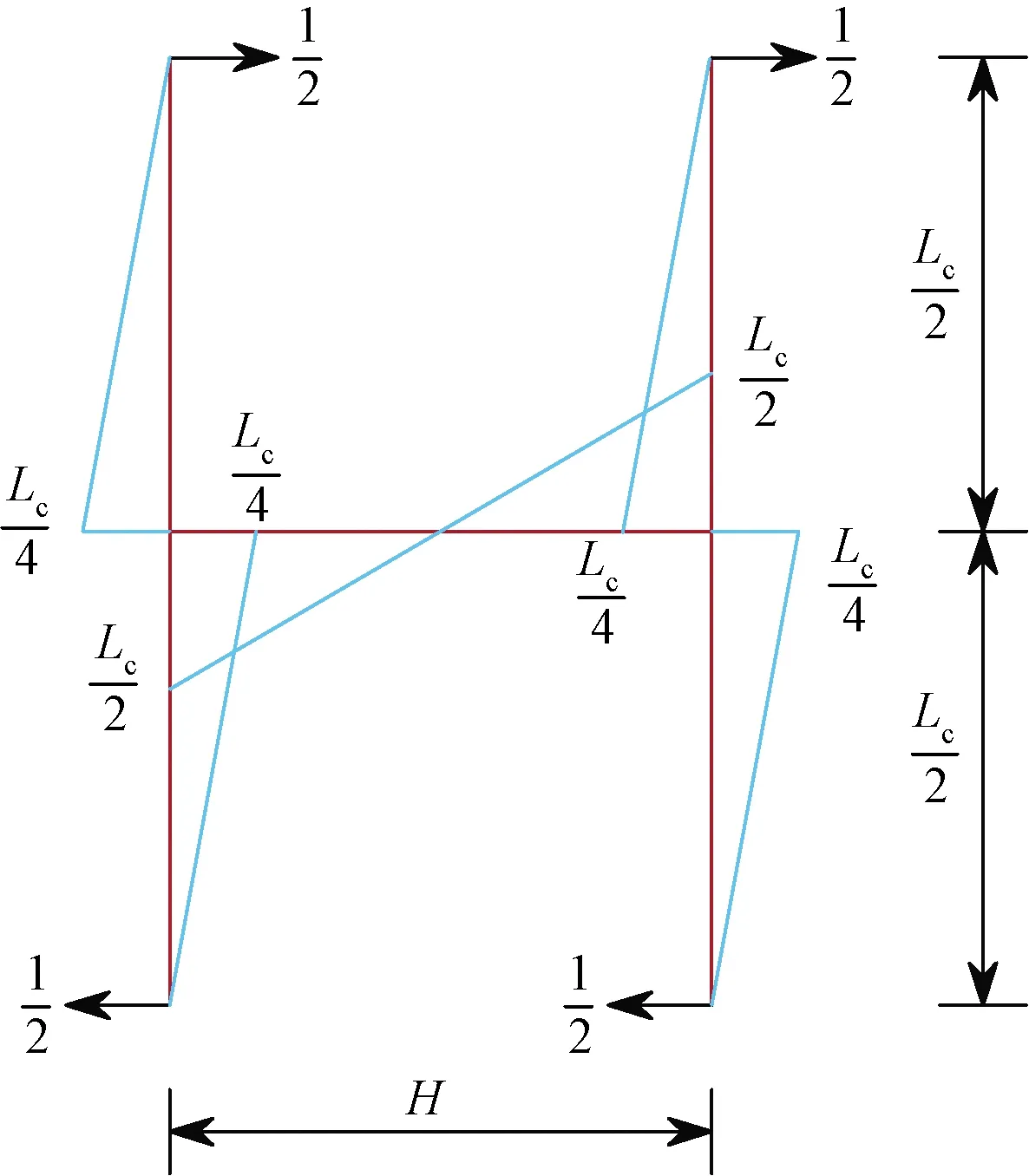
图5 剪力作用下弯矩分布Fig.5 Moment distribution under pure shear

钢管混凝土空腹拱在每一个节段的位移δ、单位剪切角γ和换算长度系数μ可表示为

(1)

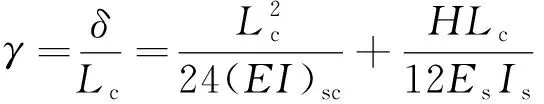
(2)

(3)

式中：Esc=(EsIs+EcIc)/Isc；Isc为截面总惯性矩(Isc=Is+Ic)；Is和Ic为钢管截面和混凝土核心截面惯性矩；Ec为混凝土的弹性模量；Es为钢管的弹性模量；lx为拱肋有效长度，对于无铰拱lx=0.36S(S为拱轴线弧长)；换算长细比λox使用公式λox=μλx计算，其中，λx为钢管混凝土空腹拱截面绕虚轴的名义长细比。

3 钢管混凝土空腹拱平面内轴压稳定设计方法

殷海棠[13]对大长细比抛物线形钢管混凝土的稳定系数提出修正公式，其考虑矢跨比的修正公式为

(4)

式(4)中:φ为稳定系数；λn为正则长细比，其计算公式为

(5)

式(5)中：Asc为钢管混凝土截面面积(Asc=As+Ac)；As和Ac为钢管面积和核心混凝土面积；fck为混凝土抗压强度标准；ξ为混凝土约束系数。

在实际模型根据ABAQUS考虑材料非线性、几何非线性后计算稳定系数时，采用方程和方程计算。

稳定系数φ：

(6)

轴心抗压承载力Ny:

(7)

式中：Nac为采用弧长法计算后钢管混凝土空腹拱在极限状态下的最大轴力[5]。

从图6中可以分析出，有限元计算出来的稳定系数大部分位于修正稳定系数公式上，表明按照修正稳定系数公式可用于预测钢管混凝土空腹拱在均布荷载下的承载能力，可用于指导钢管混凝土抛物线空腹拱的实际工程，并为研究钢管混凝土抛物线空腹拱在平面内的轴压稳定承载力提供参考。

图6 有限元与修正公式对比Fig.6 Comparison of finite element method and modified formula

4 钢管混凝土抛物线空腹拱压弯作用下线性静力分析

为了研究拱中压力和弯矩的变化规律，对钢管混凝土抛物线空腹拱进行一阶线弹性分析。在含钢率为0.08、换算长细比为100的情况下，对矢跨比1/9、1/6和1/4.5的钢管混凝土空腹拱在常见荷载工况下进行研究，其变化趋势与Liu等[11]相似。在跨中集中荷载(P=1 kN)、全跨均布荷载(qL=1 kN)和半跨均布荷载(qL/2=1 kN)的作用下，不同矢跨比的拱肋轴力和弯矩分布如图7所示。在对称加载时，轴向力分布均匀，而对于非对称加载，轴向力分布不均匀。故与钢管混凝土柱不同，钢管混凝土拱在压弯共同作用下的平面内稳定性能应考虑非对称加载作用下的轴力不均匀分布。此外，在不同的加载条件下，当拱的弯矩分布有明显的变化时，如果选择最大弯矩作为设计弯矩，则预测结果相当保守。因此，对不同的荷载情况应该考虑轴力的不均匀分布和弯矩的不均匀分布的影响，在压弯共同作用下的设计方法应该提供轴力不均匀系数和弯矩不均匀系数。

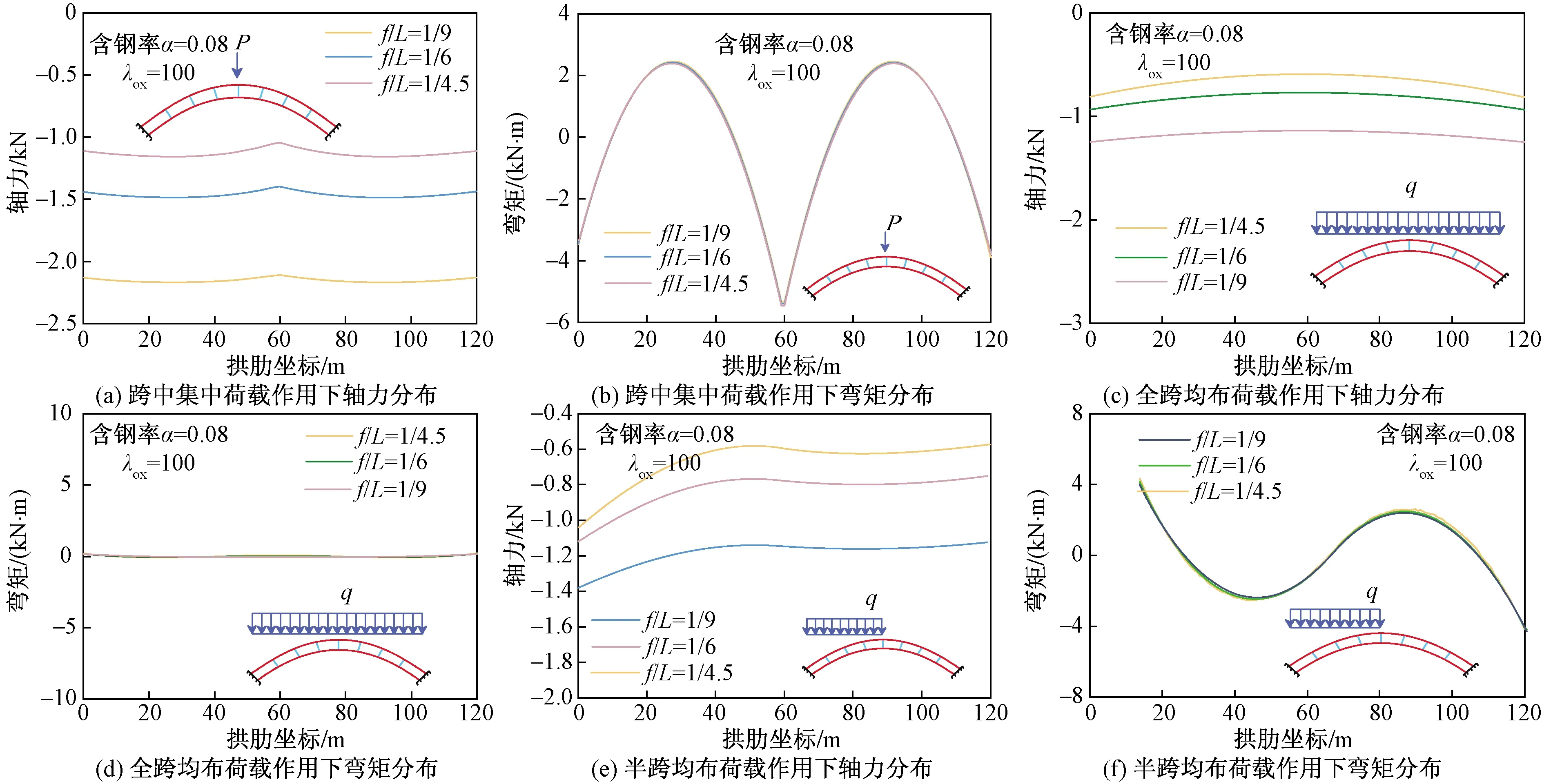
图7 钢管混凝土空腹拱内力分布的弹性分析Fig.7 Internal force distribution of concrete filled steel tubular vierendeel arch from elastic analysis

5 钢管混凝土抛物线空腹拱的全截面塑性弯矩

在钢管混凝土拱受到压弯共同作用时，钢管混凝土截面的全截面塑性弯矩是平面内强度校核的一个重要参考值。Han[20]的试验结果表明，当钢管混凝土在纯弯曲状态下截面达到极限塑性阶段时，此时拉应变比较大，最大拉应变大于10 000 με。这表明，当钢管混凝土结构在纯弯曲下达到其全截面塑性弯矩时，受拉区的混凝土已经开裂。因此，在推导钢管混凝土的全截面塑性弯矩时，应忽略受拉区混凝土的影响[21]。本文研究的钢管混凝土空腹拱有两根弦管，如图8所示。当空腹拱达到全截面塑性弯曲时，受压区面积(Asc)、受拉区面积(As1和As2)为

(8)

As1=Dtθ

(9)

As2=πθt

(10)

式中:θ为拉压区分界角。

由于截面产生的拉应力和压应力相等，故：

Ascfsc=As1fy+As2fy

(11)

式中：fy为钢管抗压强度标准值；fsc为组合抗压强度标准值，即

图8 塑性状态下的应力分布Fig.8 Stress distribution during plastic status

(12)

根据方程[式(12)]的等式，采用二分法，利用Python语言编写程序，可以求得角度θ。

受压荷载中心到上弦截面中心的距离xsc为

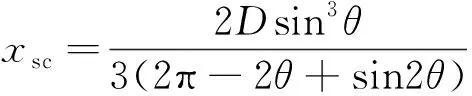
(13)

上弦受拉荷载中心到上弦截面中心的距离xs为

(14)

则全截面塑性弯矩Mp为

Mp=Ascfscxsc+As1fyxs+As2fyH

(15)

6 钢管混凝土空腹拱压弯共同作用下平面内稳定设计方法

在实际工程中，通常采用一阶线弹性方法来求拱肋的最大轴力与最大弯矩。内力的分布不仅取决于矢跨比，还取决于荷载的形式和位置[22]。为了考虑这些参数，建议将拱中的轴向力和弯矩之间的关系表示为

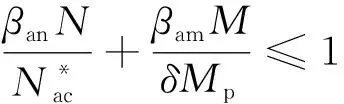
(16)

(17)

对于轴力不均匀系数(βan)；因为钢管混凝土抛物线空腹拱在对称荷载作用下轴力分布较为均匀，所以βan=1。而在不对称荷载作用下，轴力分布不均匀，从图8(e)可以看出，随着矢跨比的增加，轴力分布越不均匀，平均轴力与最大轴力之比在0.65～0.86，因此，为了简化设计方法，且偏于保存，选择最大轴力的0.9倍作为设计轴力(βan=0.9)。

钢管混凝土抛物线拱的弯矩不均匀系数的定义与钢拱的弯矩不均匀系数相同。然而，要简单地定义一个系数来考虑复杂的弯矩分布及其对矢跨比和荷载模式的依赖性并不容易。为了获得该系数，对换算长细比为60～150，含钢率为0.04～0.12，矢跨比为1/9、1/6和1/4.5的钢管混凝土抛物线空腹拱进行研究，使用计算出的极限荷载进行一阶弹性分析[22]。预测出的最大轴力与最大弯矩代入方程中，如图9所示。图9的计算结果位于等式计算结果的上方，这意味着设计实例的稳定能力始终高于公式中的预测能力，可以安全的用于工程设计中。表1给出了βam的值，且表1中的参数值可用于预测钢管混凝土抛物线空腹拱在弯矩和轴力共同作用下的平面内稳定承载力,表1中结果与Liu等[11]中大致相同。

图9 有限元结果与式(16)对比Fig.9 Comparison between FE results and Eq. (16)

表1 轴力与弯矩不均匀系数取值

7 结论

(1)利用有限元软件ABAQUS建立钢管混凝土抛物线圆管拱的模型，通过将有限元结果与实验结果相对比，稳定承载能力最大相差为8.33%。结果表明用本文提及的建模方法可以准确地模拟钢管混凝土抛物线圆管拱的稳定承载力，进而可以正确的模拟钢管混凝土空腹拱稳定承载力。

(2)利用Python语言提取有限元软件计算结果，采用考虑矢跨比的钢管混凝土抛物线空腹拱在均布荷载作用下的平面内修正稳定设计公式。由有限元计算得到的结果基本都位于修正公式上。故采用修正稳定设计公式能预测钢管混凝土空腹拱在轴压下的稳定承载力，可为工程提供参考。

(3)在压弯共同作用下，提出钢管混凝土抛物线空腹拱考虑轴力和弯矩的分布不均匀系数的稳定承载力设计公式。与有限元计算比较，该公式可以安全地用于计算钢管混凝土抛物线空腹拱在压弯共同作用下的平面内稳定承载力。