基于近邻成分分析的短期风电功率集成预测
2022-06-14姚岱伟崔双喜戚元星
姚岱伟, 崔双喜, 戚元星
(新疆大学电气工程学院, 乌鲁木齐 830047)
随着新能源技术和工业的进一步发展,风电装机容量占比越来越大。由于风力资源受到气象条件的制约,其波动性、间歇性等不稳定特性对电力系统稳定运行和优化调度带来了巨大的挑战[1]。精准的风电功率预测是提高电力系统经济运行效率,减少系统备用容量,保证电网安全稳定运行[2],提高风电消纳水平,优化电力市场的重要方法[3]。
短期风电功率预测方法可分为物理模型、时间序列和人工智能模型。目前研究以人工智能模型为主,可分为神经网络和统计学习模型,具体包括长短期记忆网络[4],高斯过程回归[5](gaussian process regression,GPR),最小二乘支持向量机[6](least squares support vector machine,LSSVM),极限梯度提升树[7]等。为改善模型的预测性能,已有大量研究对单一模型的结构或参数进行优化,文献[8]采用遗传算法优化卷积和长短期记忆混合神经网络;文献[9]采用缎蓝园丁鸟优化算法对LSSVM的超参数进行寻优,均获得了更高的风电预测精度。这种方法改善了原本的模型的弊端,提升了预测性能,但单一模型呈现的假设空间有限,难以精确描述潜在的真实假设。集成预测不局限于单一模型,而是将多个预测器组合,协调工作共同完成预测任务。为训练出具有差异的一测器,一种方法是基于某一学习算法,通过设置不同的数据结构或模型参数生成同质的预测模型,常用方法包括Bagging[10]和Boosting[11],文献[12]采用自适应提升算法将BP神经网络集成,通过误差平方倒数优化BP网络的结合权重,有效地改善了预测模型的泛化能力。但同质模型基于相近的假设空间,差异性较小。另一种方法是采用不同的学习算法产生异质预测器,研究以结合策略为主。除了以传统的简单平均法和加权平均法,文献[13]采用三种异质模型预测风电功率,以约束最小二乘回归(constrained least squares regression,CLS)作为结合策略,改进预测精度,虽然每次预测前对CLS重新训练,但CLS产生的是依然是固定的结合权重,难以适应风电功率的变化特性。以上研究表明,集成预测模型可有效避免单一模型或方法的弊端,异质预测器可反映多个假设空间,但需要进一步改进结合策略。
预测模型学习到的映射关系依赖给定的训练样本输入特征,除了对预测模型参数或结构的改善从而提升预测性能之外,引入关于数值天气预报(numerical weather prediction,NWP)的特征工程也是改善模型预测性能的有效手段。目前已有大量研究针对NWP特征选择与提取。文献[14-15]采用最大相关-最小冗余(minimal redundancy maximal relevance,mRMR)提取NWP特征子集,并分析了不同特征子集对预测精度的影响。文献[16]采用深度自编码器对NWP和历史功率信息降维,该方法具有优越的降维和原像重构性能。文献[17]采用核主成分分析挖掘特征信息,避免“维数灾”问题,提升了预测性能。以上研究表明,NWP特征工程可进一步挖掘影响功率的深度信息,不仅减少预测模型的训练时间,也对预测性能也有很大的提升,但没有考虑特征重要性程度的差异对预测效果的影响,可引入特征权重进一步优化特征空间。
针对上述问题,现提出一种基于NCA特征加权和Stacking集成学习的短期风电功率预测模型。首先利用NCA计算历史样本的NWP特征权重,构建加权输入特征。然后分别构建多组异质的预测器用于预测风电功率。最后,以多个预测值作为特征输入,以GPR模型作为结合器,将风电功率预测值融合,构建Stacking集成预测模型。通过对2014全球能源预测竞赛实际风电功率数据的预测分析和比较,验证该方法的有效性和优越性。
1 算法原理
1.1 近邻成分分析原理
近邻成分分析[18]同属于度量学习和降维领域,学习算法基于随机K近邻模型(stochasticK-nearest neighbor,SKNN),以留一验证误差最小作为优化目标,寻找最优特征权重,其学习过程就是降维过程,训练结果为特征权重。NCA原理如下。
对于包含n个样本的训练集:
S={(xi,yi),i=1,2,…,n}
(1)
式(1)中:xi为p维特征向量;yi为输出值。学习目标为根据输入特征x在给定的样本集S下预测输出值y。假定存在一个随机回归模型具有如下特点。
(1)从S中随机选择一个样本Ref(x)作为x的参考点(样本)。
(2)将x的预测值设置为参考点Ref(x)的输出值。
该方法选择最近点的输出作为预测值,类似于1-NN方法。在NCA算法中所有点都有可能被选作参考点。根据距离函数dw,与x的邻近程度越高被选作的参考点的概率越高,dw计算公式为

(2)
式(2)中:xir和xjr表示第i个和第j个样本点对应第r个特征的数据值;wr为第r个特征对应的特征权重。假设选中xj为参考点的概率满足:
P[Ref(x)=xj|S]∝k[dw(x,xj)]
(3)
式(3)中:Ref(x)为从样本集S中选取出x的参考点;k为核函数或相似性函数;dw越小则k越大,k的表达式为

(4)
式(4)中:exp表示以自然常数e为底的指数函数;σ为核宽度,用于控制每个点被选中的概率,如果x中所有特征在同一尺度,σ选定为1是合理的,因此在计算前需要对数据归一化。
从S中选取某一点xj作为参考点的概率为
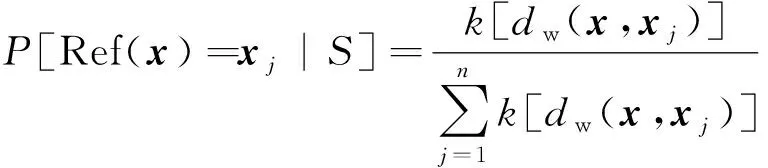
(5)
式(5)中:距离度量dw受特征权重wr影响,从而间接影响xj被选作参考点的概率。
为调整模型中特征权重wr,使用留一法预测S中xi的输出值,此时训练集S-i中不包含样本(xi,yi),则xj被选作xi参考点的概率为
pij=P[Ref(xi)=xj|S-i]

(6)
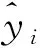

(7)
式(7)中:E为期望运算。在此基础上引入正则项,作为最小化目标函数:
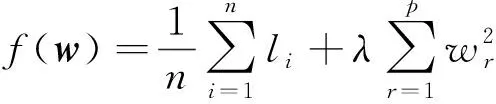
(8)
式(8)中:w为由特征权重wr构成的向量;正则化参数λ> 0,可以驱使w中某些特征权重变为0。根据给定的超参数σ和λ,优化任务为寻找合适的权重向量w使目标函数最小化:

(9)
该优化问题的最终解w元素的大小反映了各个特征的权重,从而实现特征选择和加权的功能。
1.2 Stacking集成预测原理
集成学习是一种模型融合的框架,可以将不同预测模型融合以改善单一模型的预测精度或泛化能力[19],在预测领域中称为集成预测,包含基预测器和结合策略两个重要部分。集成预测模型中基预测器应具备较好的预测能力且具有较大的差异性,差异性在于预测器采用不同的数据结构或学习算法训练,从不同的空间观测角度反映NWP特征到风电功率的映射关系。传统的结合策略以简单平均或加权平均为主,当样本规模较大时以机器学习模型作为结合策略可以进一步提升模型的预测性能,作为结合策略的模型称为元学习器或结合器,该方法即为Stacking集成预测。和其他集成方法一样,Stacking集成预测模型关注基预测器的差异性,而改善预测性能的任务由结合器完成。
在Stacking集成模型中,结合器同样需要学习产生,训练结合器的样本输入是基预测器的输出,输出对应原样本的输出。由于基预测器对原训练集的拟合程度很高,如果直接用基预测器的训练集产生结合器的训练集,容易导致最终模型过拟合,即结合器无法学习到结合策略对应的映射关系。因此一般采用k折交叉验证或留出法分别训练两层模型。以留出法为例,按比例将历史样本集划分为训练集和测试集。首先通过训练集训练多个基预测器,训练完成后,将验证集样本的输入特征输入基预测器,预测值和验证集的输出构成结合器的训练样本。采用留出法的Stacking模型学习流程的伪代码如表1所示。留出法适用于样本数量较多的情况。而k折交叉验证将上述过程遍历k轮,可得到数量相同的样本用于结合器的训练。但每次遍历都需要重新训练基预测器,计算开销较大,在大规模的样本集的预测任务中难以适用。

表1 Stacking集成预测流程
2 短期风电功率预测模型的建立
2.1 集成预测模型的基预测器和结合器
模型输入特征为预测时刻的NWP数据,来源于气象部门的预测,数据含有噪声,基预测器应具有较好的鲁棒性。因此选取GPR、SKNN、分类回归树(classification and regression tree, CART)、LSSVM和极限学习机(extreme learning machine, ELM)作为基预测器,同时选取GPR作为结合器。各个模型的原理和特点如下。
(1)SKNN:传统的KNN模型预测值根据确定的K个近邻的输出值表示,在SKNN中所有的样本都可能被选作近邻,被选中的概率由相似性函数给出,SKNN的预测值即为期望值。
(2)GPR:基于贝叶斯框架实现映射函数从先验分布到后验分布的转换,同时也是一种基于核函数的方法,训练过程就是超参数寻优的过程。
(3)CART:基于树形结构,通过一系列决策过程实现分类或回归功能。CART采用二分法简化决策树规模,使用基尼系数作为划分变量的标准,生成效率高,鲁棒性好。
(4)LSSVM:通过核函数将原始特征映射至高维空间进行回归,将SVM训练中的凸优化过程转化为求解线性方程组,提高了训练速度。模型的性能对惩罚因子和核参数较为敏感。
(5)ELM:网络结构基于传统的单隐层神经网络,输入层和隐含层的权值阈值随机产生,隐含层输出层的权值通过线性方程组求解得出,较传统的BP算法具有训练速度极快、泛化性强等优点。
基预测器SKNN、GPR和LSSVM中含有距离度量结构,采用加权NWP特征可强化关键特征对距离度量的影响程度,进而改善模型预测性能。此外,权重大的特征具有更大的方差和取值范围,进而具有更大影响程度,因此也选用加权特征作为CART和ELM的输入。
采用留出法的方式训练Stacking预测模型,避免训练时间过长。考虑到在预测时刻NWP特征已知,为了使训练出的模型更适用于预测时刻的情景,采用加权KNN搜索选取与预测时刻中样本相似度最高的一部分样本作为验证集,这部分样本可以训练结合器使之沿着适应预测时刻样本的方向修正基预测器的预测结果。
2.2 预测流程
预测流程主要包括NWP特征选择与加权、训练Stacking集成预测模型和预测3个方面。短期风电功率集成预测流程如图1所示,步骤描述如下。

图1 风电功率预测流程Fig.1 Flow chart of wind power prediction
步骤1以历史数据的NWP气象验证和风电功率构建历史样本集和预测时刻的输入特征,并将样本数据归一化。
步骤2采用NCA计算模型历史样本的输入特征权重,并对筛选后的特征加权。
步骤3根据预测时刻输入特征采用加权KNN算法在历史样本中所搜相似样本,将历史样本划分为训练集和验证集,训练Stacking集成预测模型。
步骤4将预测时刻NWP特征输入集成预测模型,得到风电功率预测值。
2.3 预测评价指标
选取标准均方根误差(ENRMSE)和标准平均相对误差(ENMAPE)作为衡量预测精度的评价准则[20],计算公式为

(10)
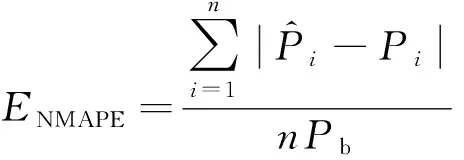
(11)
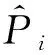
3 算例分析
基于2014全球能源预测竞赛数据进行建模与算例分析。原始数据包含10个风电场的功率出力,以及同时刻10 m和100 m高的经向和纬向风速的预测值,时间分辨率为1 h。数据中10个风电场的具体位置未被披露,但预测某一风电场功率出力时依然可以考虑场外数据[21]。因此选取10个风电场,共40组风速数据作为输入特征,以3号风电场的功率出力作为输出值,构建原始样本集。考虑到风电功率对风速更敏感,将原始特征的经纬风速转换为风速和风向特征。
选取两组预测时段作为测试集,分别为2012年9月7—13日和2013年3月7—13日。每组测试集预测时刻点数为168,并将前180日数据作为训练集。
3.1 NCA气象特征加权及验证
采用NCA计算预测时刻NWP特征权重,原始数据采用Z-score归一化,内核宽度σ设置为1。模型中正则化参数λ采用贝叶斯优化算法寻优(图2),搜索区间为(0, 1],根据加权SKNN在训练集的5折交叉验证的预测均方误差作为目标函数,最终λ设置为0.001 4。经计算得到各个特征的权重分布如图3所示。

图2 λ寻优过程Fig.2 Optimization process of λ
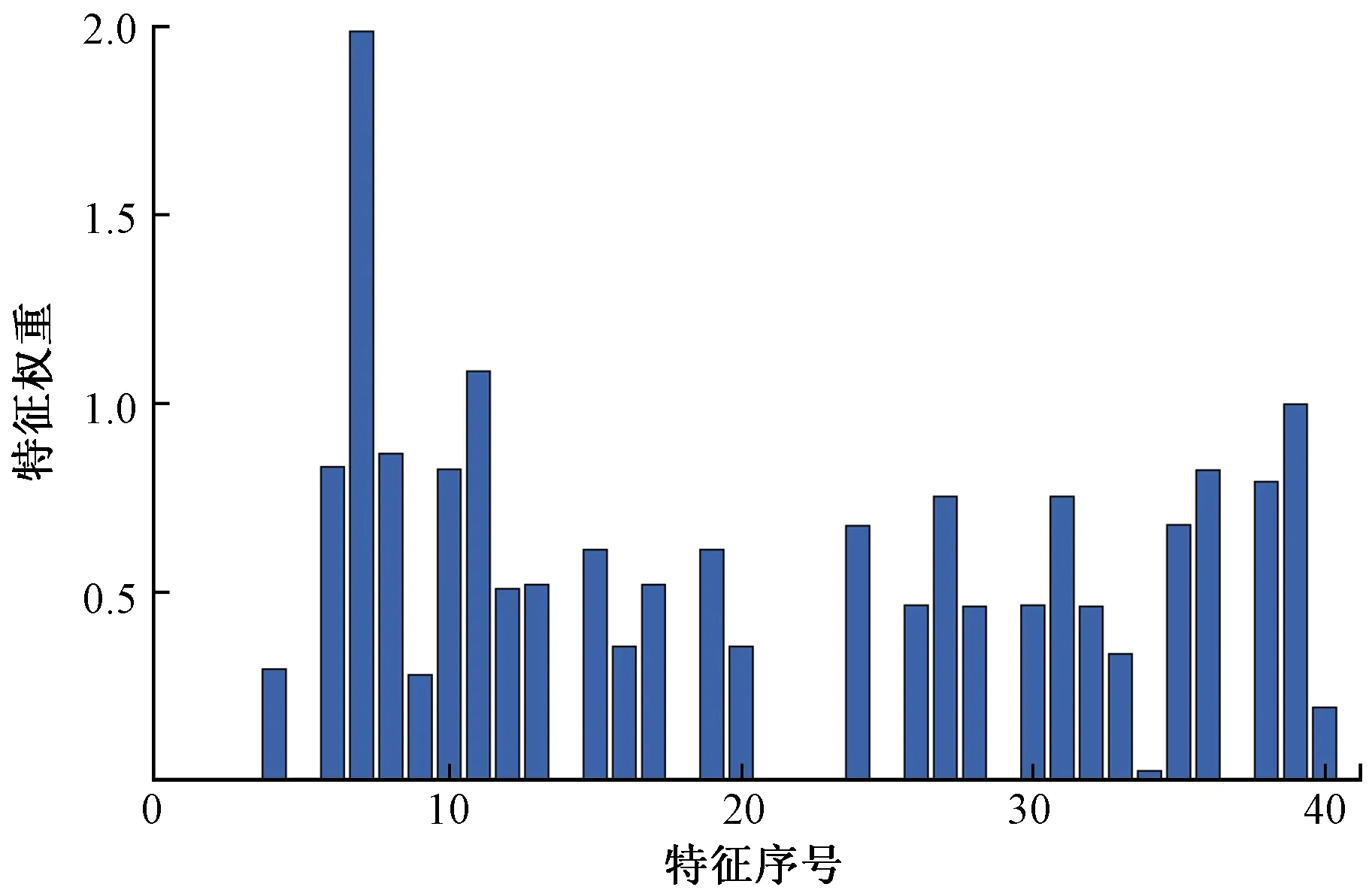
图3 特征权重分布Fig.3 Feature weight distribution
为验证NCA特征加权的有效性,选取mRMR、主成分分析(principal component analysis,PCA),灰色关联分析(grey relation analysis,GRA)进行对比。其中mRMR计算出特征的重要性评分,GRA计算出每个特征和功率的关联度,可根据指标分配相应的权重。PCA是一种特征提取方法,变换后的主成分中已经包含了重要性信息,因此PCA选取贡献度大于95%的前12个主成分作为输入。将上述加权特征作为预测模型SKNN的输入特征,计算不同方法在第一组验证集的预测误差,预测误差如表2所示。
以2012年9月7—13日的预测时段为例,当输入特征为NCA加权特征时,预测误差最小,其ENRMSE较mRMR降低了3.65%,较GRA降低了3.9%,较PCA降低了4.03%,其ENMAPE同样优于其他特征加权方法。另一预测时段具有相同的规律。说明基于NCA特征加权可以有效改善模型的预测性能,提高短期风电功率预测精度,因此在预测之前引入NWP特征加权有效可行的。

表2 不同特征加权方法预测误差对比
3.2 预测结果对比
在训练之前按照2.2节中方法划分训练集和验证集。为了控制训练集和验证集的比例规模,选取每个测试样本的10个近邻样本作为验证集,最终选取的验证集占历史样本比例约为15%。
模型的超参数都会对其预测性能有较大影响,为使最终的预测效果达到最优,需要对超参数进行寻优。基预测器SKNN预测过程基于训练样本,不包含任何参数。其余模型的超参数优化根据预测时段2012年9月7—13日的训练集计算得出,最终确定的超参数结果如表3所示,另一预测时段的预测模型设置相同的超参数。
为验证Stacking集成方法对预测性能的改进和合理性,现将其预测结果和基预测器进行对比。两组预测时段的风电功率预测曲线和实际曲线如图4所示,预测误差ENRMSE和ENMAPE如表4所示。
以预测时段2012年9月7—13日为例,从表4可看出,基预测器中SKNN和GPR预测精度相当,优于其他3种预测器。集成预测模型将五组预测结果融合,ENRMSE和ENMAPE较GPR分别降低了0.66%和0.89%,优于单一模型。而另一预测时段风功率较低且较平稳,基预测器均具有较高的预测精度,集成后预测误差ENRMSE和ENMAPE较CART分别降低了1.57%和1.13%,有更显著的下降。因此,融合多预测器的Stacking集成模型可显著提高预测精度。

表3 各类模型的参数

表4 不同预测模型预测误差对比

图4 风电功率预测曲线Fig.4 Curves of wind power prediction
为进一步验证Stacking集成模型以结合器GPR作为集成策略的有效性,对不同结合策略下集成模型的预测性能进行比较。另选取最小二乘(least squares regression,LSR)回归,简单平均法和基于误差倒数加权平均法作为结合策略。预测曲线和预测误差对比分别如图5和表5所示。
对比表5各个结合策略的集成模型可看出,采用简单平均法作为结合策略,得到的集成模型预测误差接近预测性能最佳基预测器。误差倒数法根据基预测器在验证集的误差ENRMSE倒数分配组合权重,较简单平均法预测性能有所改善,但实际上由于基预测器的误差比较接近,导致其分配的权重大小相当,其性能和简单平均法接近。
相较于传统的结合策略,以机器学习模型作为结合策略具有更高的预测精度。LSR即线性回归,学习能力弱于GPR,但LSR作结合器依然使集成模型预测误差有所降低。在两组预测时段ENRMSE比最佳的基预测器降低了0.37%和0.94%,ENMAPE降低了0.34%和0.27%。而学习能力更强的GPR作为结合器进一步减少预测误差,ENRMSE进一步降低了0.29%和0.63%,ENMAPE降低了0.55%和0.89%。说明以学习能力更强的GPR作为集成预测模型的结合策略是进一步改善集成预测性能有效方案。

图5 不同结合策略风电功率预测结果对比Fig.5 Comparison of wind power prediction results by different combination methods
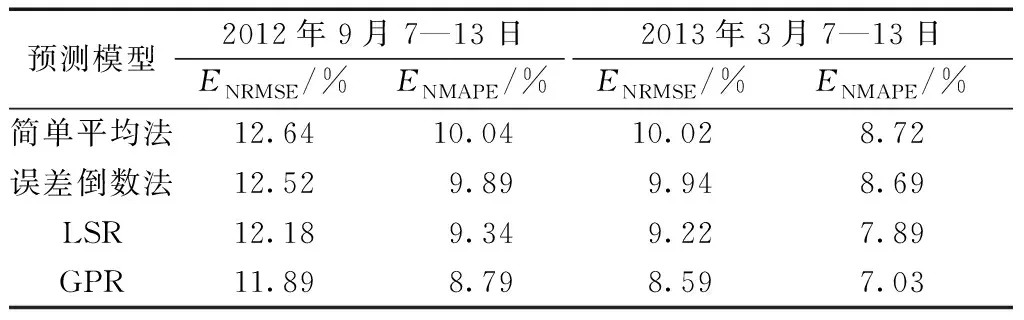
表5 不同结合策略的预测误差对比
4 结论
以提升短期风电预测精度为目标,提出一种基于NCA特征加权和Stacking集成预测的短期风电功率预测模型。经过分析研究,得出以下结论。
(1)特征权重可以优化特征空间,改进模型预测性能,NCA特征加权优于其他方法。
(2)集成预测模型可以避免单一方法预测性能的局限性,得到比单一模型更高的预测精度。
(3)相较于简单平均法和误差倒数法,以学习能力较强的GPR作为Stacking集成预测模型的结合策略可进一步降低预测误差,其性能优于以LSR作为结合策略的Stacking集成预测模型。
预测模型的差异性是集成预测的关键,本文选取的输入特征仅考虑了预测时刻,未考虑其时序性。如何从多特征类型建立集成预测模型将是下一步研究的内容。
