输入延迟系统的切换伪预测镇定控制器
2022-06-16梁家豪唐予军王霞
梁家豪,唐予军,王霞
(河北大学 电子信息工程学院,河北 保定 071002)
在许多工程应用中,控制系统经常会产生一些延迟现象,例如网络控制[1-2]、数据传输[3]、无线通信[4]等,这些延迟现象会对系统的稳定性及其性能产生不利的影响,因此,引起了学者们研究延迟系统的兴趣.在过去的几十年中,学者们对延迟系统进行了大量的研究[5].
在现有文献中,延迟系统稳定性分析及镇定的方法主要包括基于Lyapunov-Krasovskii泛函的方法[6]和设计预测反馈控制器的方法.文献[7]研究了具有输入延迟的连续互联系统基于预测变量的镇定问题.文献[8]通过预测变量链研究了同时具有状态输入定常延迟和输出延迟的线性系统的稳定性问题.该方法与线性矩阵不等式有很大的关联,所以在系统反馈控制器的设计中经常使用,而这种方法的基本思想是找到一个正定函数,使其沿延迟系统轨迹的时间导数是负定的.利用这种方法进行镇定、跟踪等控制器设计能够确保状态或误差收敛,但难以分析和描述整个闭环系统的收敛动态,即使是线性被控系统,也难以用闭环特征根位置分析系统的收敛特性.在实际应用中,稳定是最基本的要求,工程师们关注更多的是系统的动态.文献[9]通过构造多分布输入延迟下的预测反馈控制,从而使闭环系统指数稳定.文献[10]提出一种称为嵌套预估器反馈的新方法,用来研究长输入延迟补偿问题.当延迟时间为时变的且系统为非线性系统时,预测器的方法依然有效.文献[11]为一种时滞系统设计了改进无模型自适应预测控制器,使延迟系统稳定.文献[12]研究了一种高能随机非线性系统,设计了一个自适应神经网络预测控制器,使得闭环系统在任意切换下所有信号有界.当预测器提供的预测状态与系统未来状态一致时,利用预测状态进行控制相当于去掉了控制通道中的延迟,从而使常规设计方法得以应用,只是用开环系统进行系统未来状态的预测,会产生关于输入的积分项,而输入的积分项只能通过数值分析的方法进行求解,故所设计的预测器便不易于实现.为了避免预测器中输入积分项的影响,文献[13]提出伪预测反馈(pseudo predictor feedback,PPF)控制,用于解决单输入延迟系统的镇定问题.传统的预测器反馈控制使用开环系统动力学预测未来状态,与传统的预测器不同,而PPF使用的是闭环系统动力学预测系统的未来状态,这样得到的控制器避免了预测器中输入积分项的影响,更加容易实现.文献[14]中的PPF还可用于具有多个分布式输入的延迟系统的控制器设计[13,15].但是在最初的延迟时间段内,由于控制作用还未对系统状态产生影响,伪预测器给出的预测状态并非系统未来状态,这会对系统动态的初始部分造成不可预测的影响.
本文提出一种切换伪预测器,并在此基础上构造预测反馈控制器,用于镇定具有输入延迟的系统.以延迟时间为界将原系统分为开环和闭环2个子系统,再利用相应子系统的解,分别构造延迟系统的子伪预测器,使子伪预测器按照延迟时间切换,从而精准预测系统未来状态.切换伪预测器中同样不存在输入的积分项易于实现.利用切换伪预测器为延迟系统构造镇定控制器,证明了闭环系统的稳定性.仿真表明,切换伪预测控制器能够准确预估系统状态,同时,利用预估状态构造的镇定控制器能够使系统渐近稳定.
1 问题描述
考虑以下带输入延迟的非线性系统
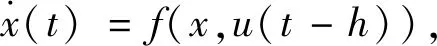
(1)
其中,f(x,u)为可积函数,x为系统状态,u(t)为系统输入,h为已知延迟时间.
假设1对于无输入延迟的非线性系统

(2)
可以设计出状态反馈控制器
u(t)=α(x),
(3)
使闭环系统
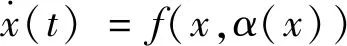
(4)
稳定.
为了消除系统(1)中输入延迟的影响,要用系统未来状态ξ(t)=x(t+h)取代式(3)中的x(t).传统的预测器依据系统(1)预测未来状态

(5)
根据控制器(3)可以得到系统(1)的控制器
u(t)=α(ξ).
(6)
由于式(5)中含有u(t)的积分项,需要使用数值分析法计算,不易于实现.故可以使用式(4)设计如式(7)伪预测器以消除u(t)的积分项,使预测器易于实现.

(7)
但是在最初的延迟时间段内,由于延迟的存在使控制信号不能对系统状态产生影响,这就会使伪预测器无法预测出系统初始部分的状态.设计切换伪预测器,使其可以精准预测系统未来状态.
2 切换伪预测器
2.1 非线性系统切换伪预测器
以延迟时间为界,将系统分为2个子系统,设计以下切换伪预测器.
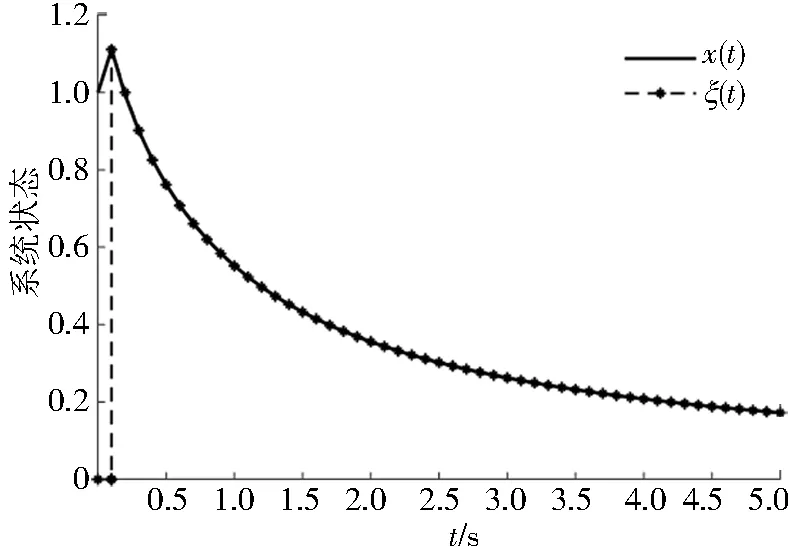
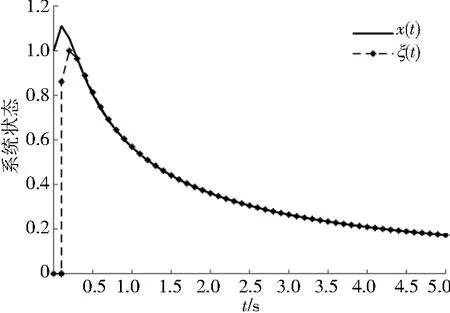
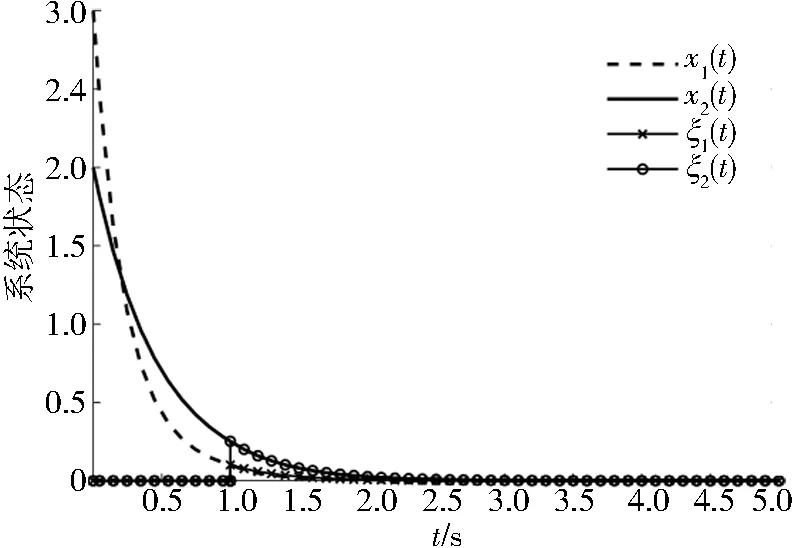
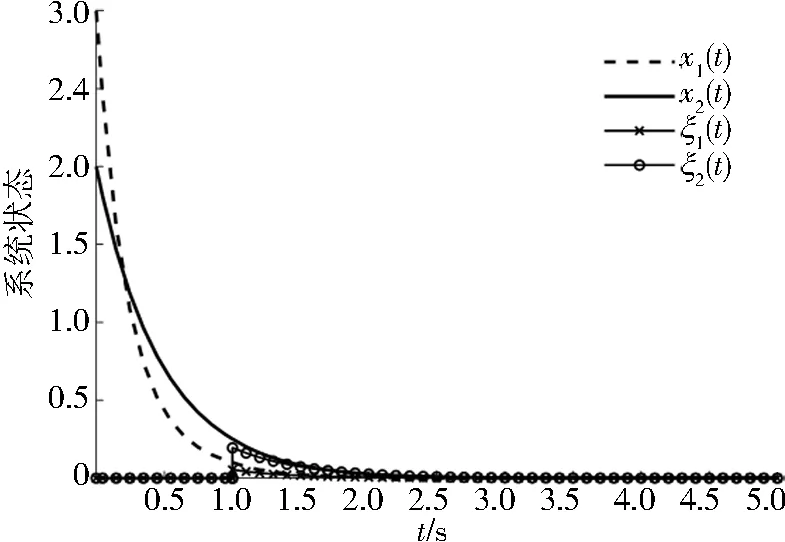
当t (8) 则系统(8)的解为 (9) 将t作为t0,h作为t可以得出 (10) 式(4)的解为 (11) 则可得伪预测器为 (12) 当t≥h时,控制信号对系统产生作用,则用式(4)预测未来状态,式(4)的解为 (13) 得到伪预测器 (14) 综上,得到带延迟的非线性系统的切换伪预测器为 (15) 将带延迟的非线性系统的伪预测器具体到带延迟的线性系统中,并且进一步给出了闭环系统稳定的充分条件. 考虑以下带输入延迟的线性系统 (16) 其中,x(t)为系统状态,u(t)为系统输入,A∈Rn×n,B∈Rn×m为已知系数矩阵,h为已知延迟时间. 同理非线性系统,以延迟时间为界将系统分为2个子系统. 当t ξ(t)=x(t+h)=e(A+BK)teA(h-t)x(t). (17) 根据式(17)设计系统反馈控制器 u(t)=Kξ(t)=Ke(A+BK)teA(h-t)x(t). (18) 将式(18)代入式(16)中得到闭环系统 (19) 当t≥h时,使用无延迟闭环系统可以得到伪预测器为 ξ(t)=x(t+h)=e(A+BK)hx(t). (20) 根据式(20)设计系统反馈控制器为 u(t)=Kξ(t)=Ke(A+BK)hx(t). (21) 将式(21)代入式(16)得到闭环系统 (22) 综上,得到带延迟的线性系统的切换伪预测器 (23) 将式(23)带入式(16)可得闭环系统 (24) 最后给出闭环系统(24)稳定的充分条件. 定理1在满足假设条件下,当且仅当积分延迟系统(integral delay system,IDS) (25) 为渐近稳定时,闭环系统(24)渐近稳定. 证明:闭环系统(24)改写成 (26) 其中, ρ(t)=K(e(A+BK)hx(t-h)-x(t)). (27) 由式(26)的解得出 (28) 将式(28)代入式(27)得 (29) 由上可知若积分延迟系统(29)为渐近稳定,则式(26)渐近稳定,因此可得闭环系统(24)为渐近稳定. 设计辅助系统 (30) 其中,r(t)满足积分延迟系统 (31) 由式(30)解得 (32) 将式(32)代入式(31)得 r(t)=K(e(A+BK)hy(t-h)-y(t)). (33) 将式(33)代入式(30)得 (34) 由此可以得出:若系统(34)渐近稳定,则式(33)为渐近收敛,因此系统(25)渐近稳定. 将积分延迟系统(25)改写成 (35) 其中, G(t,s)=-Ke(A+BK)(t+s)B. (36) 定理2若存在正定矩阵P,Q满足: (37) 则积分延迟系统(35)为指数稳定. 证明:取Lyapunov-Krasovskii泛函 (38) 其对时间的导数为 (39) 由式(35)和式(37)可得 (40) 将式(40)代入式(39)可得 (41) 由此可以得出系统(25)为渐近稳定的. 考虑以下带输入延迟的非线性系统 其中,x(0)=1,延迟时间h=0.1 s.控制器u(t)=-2x2(t). 通过计算得到带输入延迟的非线性系统的切换伪预测器为 则带输入延迟的非线性系统的切换PPF控制的仿真结果如图1所示: 图1 非线性系统切换伪预测器Fig.1 Switching pseudo predictor for non-linear systems 作为对比,带输入延迟的非线性系统的非切换伪预测器为 x(t+h)=x(t)+1/(t+h+1/x(0))-1/(t+1/x(0)). 仿真结果如图2所示: 图2 非线性系统非切换伪预测器Fig.2 Non-switching pseudo predictor for non-linear systems 考虑以下带输入延迟的线性系统 通过计算得到带输入延迟的线性系统的切换伪预测器为 则带输入延迟的线性系统的切换PPF控制器的仿真结果如图3所示: 图3 线性系统切换伪预测器Fig.3 Switching pseudo predictor for linear system 作为对比,带输入延迟的线性系统的非切换伪预测器为x(t+h)=e(A+BK)hx(t),其仿真结果如图4所示: 图4 线性系统非切换伪预测器Fig.4 Non-switching pseudo predictor for linear system 通过比较上述2个仿真结果可以看出,本文所设计的切换伪预测反馈控制器能够精准预测系统初始部分的状态,同时镇定输入延迟系统. 本文考虑了具有输入延迟系统的镇定问题,基于闭环系统为延迟系统设计了一种切换的伪预测器,使其能够精准的预测系统的未来状态,并且消除了传统预测器中的积分项,使控制器更加容易实现.最后通过数值示例说明了伪预测反馈(PPF)控制器的有效性和优势.后续工作可以对以下方面进行研究:带有不确定性的线性系统的鲁棒自适应切换控制器设计和将对非线性系统的设计应用到下三角系统中,以解决实际问题.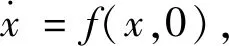





2.2 线性系统切换伪预测器
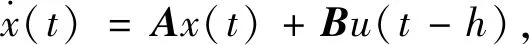

3 线性系统稳定性分析






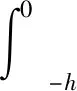

4 仿真实验
4.1 非线性系统仿真实验
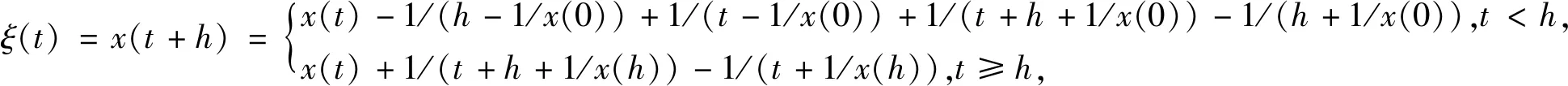
4.2 线性系统仿真实验
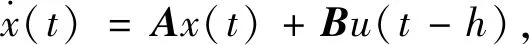
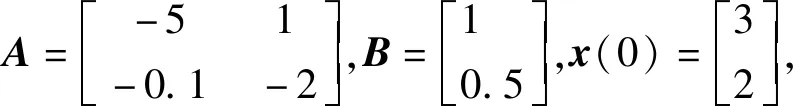
5 结论
