基于非规则分布样本的航段油耗区间估计

2022-06-14陈静杰梁国栋刘家学赵华治

科学技术与工程 2022年14期

陈静杰，梁国栋，刘家学*，赵华治

(1.中国民航大学电子信息与自动化学院，天津 300300； 2.中国民航大学中欧航空工程师学院，天津 300300)

伴随航空客运量的快速增长，飞机油耗及对应的碳排放量的显著增幅给行业稳定运行和应对气候变化方案的出台带来了巨大挑战，国际民航组织(International Civil Aviation Organization，ICAO)于2016年通过了国际航空碳抵消和减排计划(carbon offsetting and reduction scheme for international aviation，CORSIA)，随后将其写入国际民用航空公约附件16的第Ⅳ卷[1]，以国际标准的形式要求各成员国下的航空公司对航段油耗以及碳排放量进行监测、报告和核查，当航空公司缺失某航段油耗记录数据或不具备油耗监测能力时，需采用合适的方法进行估计，估计结果的合理性会被国家聘请的第三方机构核查，这为航空公司带来难题，解决问题的关键在于：能够利用飞机其他数据对航段油耗合理、准确地估计，难点在于：航段油耗样本的非规则分布特征，产生的原因有：发动机的多经济运行工作点在实际运行过程中的偏离、航空器运行姿态的包络控制以及航空器运行环境的诸多不可控因素所致。

目前，ICAO研究人员基于分段最小二乘思想开发的CO2估算和报告工具[2]可用于快速、粗略地估算航段油耗，刘菲等[3]基于雷达记录数据建立的油耗估算模型可用于分析空中交通管制技术对飞机油耗量的影响，此外，许多学者为精确估计飞机油耗，建立了基于深度学习的油耗估计模型[4-5]，但这种方法计算代价昂贵，泛化能力较弱。以上飞机油耗估计模型均为点估计模型，Turgut等[6]指出随着航程增加，航段油耗的不确定性也随之增加，油耗估计值在一定范围内都是合理的，传统点估计方法将航段油耗视为确定性变量无法表征该航段飞机实际油耗的潜在随机性，由此，有学者开展了飞机油耗区间估计的研究[7-8]，其基本思想是，先针对单一航段，估计油耗统计量，建立估计区间，后通过拟合区间上下界的方式建立基于全局的油耗估计，但在估计某航段油耗统计量时，许多学者忽略了油耗样本分布特征对模型估计性能的影响，许多基于机器学习和统计学的估计模型需假设数据呈类正态分布[9]，陈静杰等[10]首先注意到短航程航段油耗样本的双峰分布现象，然而样本的双峰甚至是多峰分布也存在于长航程航段，航空公司要具有对任意航段油耗进行合理估计的能力。

由此，在考查了诸多应用[11-14]和抽象的基础上，现使用历史航班的飞机快速存取记录器(quick access recorder， QAR)数据进行测耗区间估计，首先通过SVQR方法构建航段油耗的非线性回归模型，得到任意航段的油耗条件分位数估计值，再将一定数量的条件分位数作为Bootstrap的输入，进而对航段油耗总体的统计量进行估计，最后建立任意航段的油耗估计区间。提出的SVQR-Bootstrap航段油耗区间估计方法考虑了样本的分布特征，可为航空公司合理地估计油耗提供参考。

1 飞机航段油耗区间估计方法

航空公司为落实ICAO的CORSIA，除了需要对历史航段油耗估计外，还需对新开通以及由于种种原因导致数据缺失的航段进行油耗预测，与一般的区间估计方法思路相反，本文研究以先回归、后建立估计区间的方式构建航段油耗估计模型，其流程如图1所示。

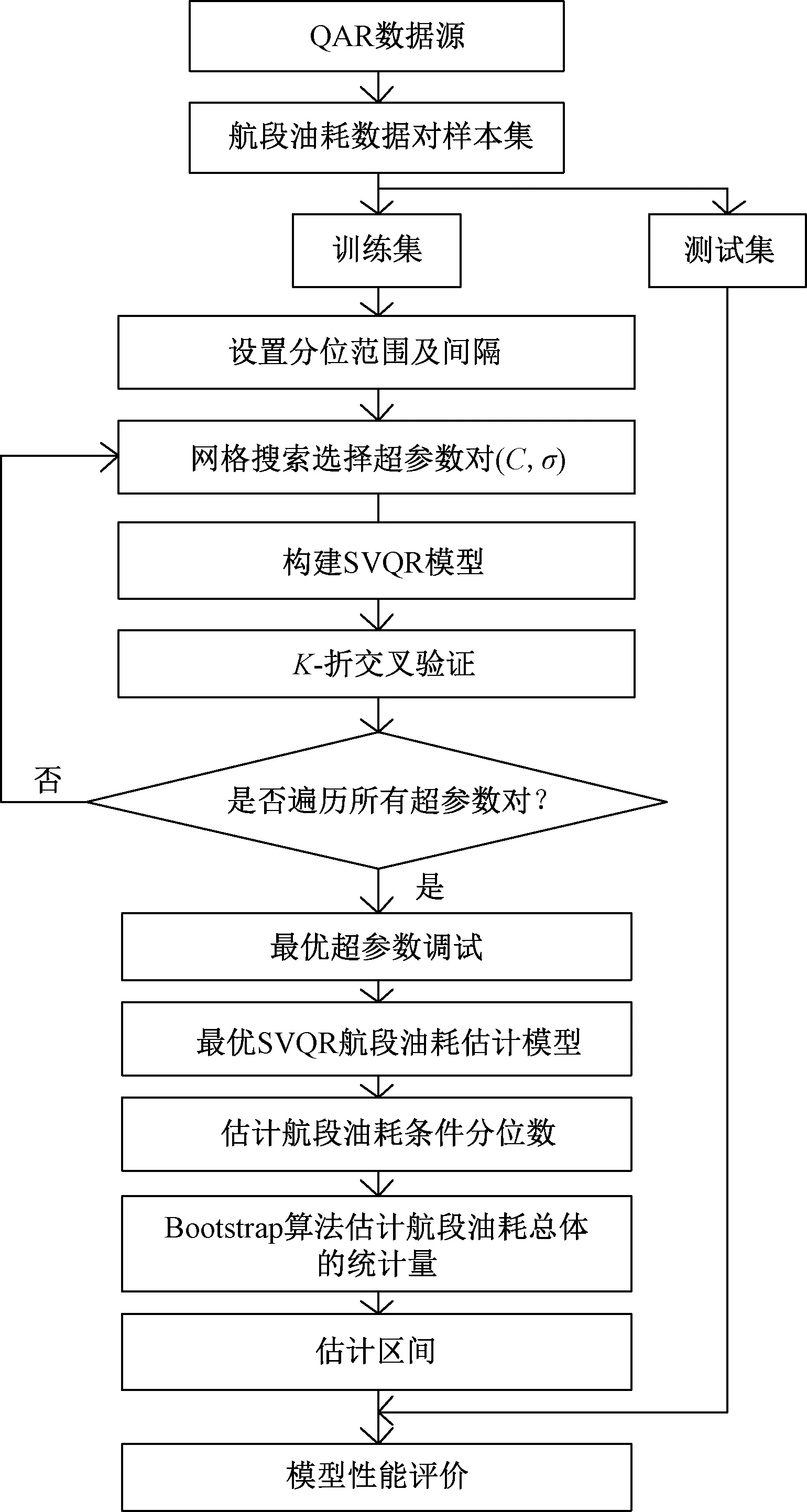
图1 SVQR-Bootstrap航段油耗区间估计方法流程图Fig.1 The flowchart of SVQR-Bootstrapflight segment fuel consumption interval estimation method

1.1 分位数回归

假设：航班的标准大圆航距和油耗数据对的样本集是：{(xi,yi)}，i=1,2,…，n，其中，xi为输入向量，表示航班的标准大圆航距，且在相同航段内航班的标准大圆航距相等；yi为期望输出向量，表示航班的油耗量。则线性分位数回归模型[15]为

(1)

式(1)中：Qyi(τ∣xi)为因变量yi在自变量xi给定条件下的τ分位数；τ∈[0,1]为分位点；β(τ)为回归系数向量,可通过式(2)求解：

(2)

1.2 支持向量分位数回归

传统分位数回归为线性模型，为将分位数回归理论应用在复杂的非线性问题上，Takeuchi等[16]首次将支持向量回归中的惩罚函数替换为非对称检验函数，提出了SVQR模型：

(3)

式(3)中：ωτ、bτ分别为τ分位点下的参数向量和阈值；C为惩罚参数；n为样本量；χ(·)为非线性映射函数；ρτ(·)为非对称检验函数。

(4)

1.3 基于SVQR的航段油耗非线性回归模型

航段油耗受多因素影响，标准大圆航距与油耗间既存在线性关系也存在非线性关系，为此，单独取出χ(xi)中的线性成分zi，本文取zi=xi作为模型的输入向量，以建立性能更优的半参数SVQR[17]航段油耗估计模型：

(5)

引入松弛变量和Lagrange乘子对式(5)求解，可得到：

(6)

(7)

式(7)中：σ为核函数的带宽。

1.4 SVQR航段油耗模型的超参数寻优方法

超参数C和σ是影响SVQR模型性能的关键因素，通常采用经验选择、网格搜索、实验试凑的方法对其寻优，但经验选择与实验试凑计法计算误差较大，网格搜索对于较大数据集计算代价较高[18]，因此，将上述三种方法相结合，以实现快速、准确的超参数寻优，步骤如下。

(1)据经验选择方法[19]，计算出经验C值和σ的取值范围，计算公式为

(8)

σ～[0.1,0.5]range(x)

(9)

式(9)中：range(x)为训练集中标准大圆航距的变化范围。

(2)根据经验C和σ缩小超参数的搜索域，构建超参数网格，通过交叉验证获得超参数的初步寻优结果。

(3)通过多次仔细调参实验，确定较优的超参数组合。

1.5 Bootstrap航段油耗总体的统计量估计

Bootstrap方法[20]是一种非参数估计方法，能利用样本统计推断总体的分布特性和统计量，对航段油耗总体统计量进行估计的基本步骤如下。

(1)Q={Qτ1,Qτ2,…,Qτt}是一组基于SVQR航段油耗估计模型得到的油耗条件分位数样本，样本容量为t。

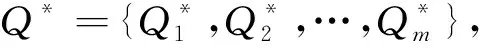
(3)重复步骤(2)B次(B足够大，B≥1 000)，得到B组Bootstrap样本{Q*(1),Q*(2),…,Q*(B)}。

(4)计算每组Bootstrap样本的统计量，可得到统计量的样本集：{T1,T2,…,TB}，则航段油耗总体统计量的估计值为

其次，“少儿万有经典文库”的作者具备深入浅出讲经典巨著的能力。优秀的少儿科普作家写作科普图书不仅需要有专业知识背景，还要有能把科学知识深入浅出地写出来的能力，也就是能够把深奥的科学知识写得通俗易懂的能力。这套文库由各研究领域有建树、影响力的专家、学者、教授讲解。他们不仅有专业的科学素养，还是儿童浅语艺术的高手，更重要的是怀有一颗童心，关爱儿童，关心民族的未来。

(10)

1.6 SVQR-Bootstrap航段油耗估计过程

(1)利用航班QAR数据，计算各航段内航班的标准大圆航距xi向量及油耗yi向量组成的数据对样本集{(x1,y1),(x2,y2),…,(xn,yn)}。

(2)采用标准化残差的方法剔除异常油耗数据，随后对数据集进行划分和归一化处理。

(3)设置分位范围及间隔，输入训练数据训练SVQR模型，由式(6)得到一定数量的估计航段油耗条件分位数。

(4)利用步骤(3)得到的油耗条件分位数作为Bootstrap方法的输入数据，由式(10)估计航段油耗总体的均值μT和标准差δT。

(5)以μT作为航段油耗的确定性估计值，根据固定机型、航段油耗总体满足正态分布，构建95%置信度的航段油耗估计区间为：[μT-1.96δT,μT+1.96δT]。

2 评价指标

选用估计区间可信度(estimation interval coverage probability, EICP)、估计区间归一化平均带宽(normalized mean estimation interval width，NMEIW)以及综合指标(coverage width-based criterion, CWC)[21]对估计区间质量进行评价。

2.1 估计区间可信度

EICP指真实值落入估计区间的概率，是估计区间可靠性的表征。

(11)

(12)

式中:Ui、Li为第i个航班所在航段的油耗估计区间的上、下限；k为测试集的样本量。

2.2 估计区间归一化平均带宽

(13)

式(13)中：R为测试集的变化范围，用于对平均带宽做规范化处理。

2.3 综合指标

区间估计的目标是较高的EICP和较窄的NMEIW，然而从理论上看，这两个目标相互矛盾，因为一旦NMEIW减小，EICP理应随之减小，为合理评价估计区间的质量，引入综合指标定量表示二者的权衡情况。

CWC=NMEIW(1+γe[-η(EICP-μ)])

(14)

(15)

式中：μ为置信度；η用于EICP<μ时施加的惩罚量，本文取η=50；γ判断是否需要对当前估计区间惩罚。

3 算例及分析

3.1 算例

3.1.1 数据收集

QAR数据以固定频率记录了完成该次飞行任务的绝大部分飞行参数，包括飞行轨迹数据，如经度、纬度、高度等；飞行环境数据，如风速、风向、总温等；飞机性能数据，如发动机燃油流量、地速、滚转角等，实验需使用标准大圆航距及相应的航班油耗数据，但这些参数在QAR数据中并未直接给出，本文研究中使用2013年机型为A330共7 278 次航班的QAR数据作为原始数据源对其进行解算，需用到如表1所示的参数，将QAR数据的首、尾经、纬度数据作为起始机场、目的机场的经纬度位置，将其转换为球面坐标系坐标，计算出两位置的直线距离，随后求出两点连接地球球心的夹角，进而获得标准大圆航距数据；将 QAR数据中左、右发动机的燃油流量分别积分再求和获得航班油耗数据。

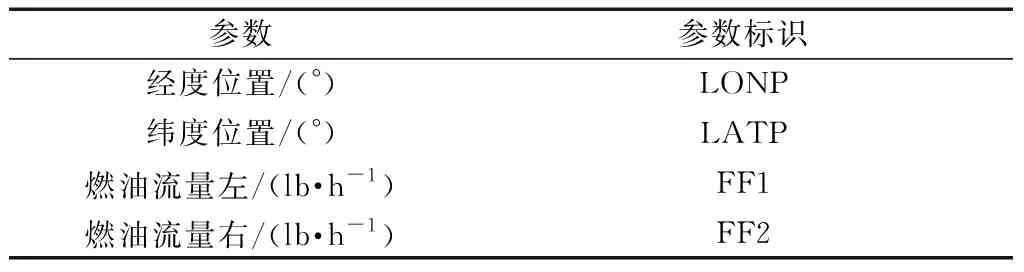
表1 实验所需的参数Table 1 Parameters required for the experiment

3.1.2 异常值的识别和剔除

极端天气、航班延误和停靠备降机场等情况会造成飞机异常油耗，本文利用标准化残差的方法识别并剔除异常油耗数据，基本思路为：先对原始油耗数据线性回归，回归结果如图2所示，其次计算出所有样本点的标准化残差绝对值，将其绝对值大于3的样本点识别为异常并剔除，如图3所示，最后将样本量少于10个的航段油耗数据剔除，得到35组，共7 056次航班的油耗数据作为模型训练和测试的数据源。

3.1.3 数据划分

对于A330型飞机，航段类型划分的标准为，短航程航段：0～2 400 km,中航程航段：2 400～4 800 km,长航程航段：4 800～11 000 km。首先随机抽取短、长航程共两个航段的历史油耗数据(PEK-ICN：北京首都国际机场—首尔仁川机场，901 km；PVG-SYD：上海浦东国际机场—悉尼金斯福德·史密斯机场，7 835 km)作为测试数据集1，以验证模型的预测性能，随后将剩余数据划分为80%的训练数据集，用于模型训练，20%的测试数据集2，用于验证模型的估计性能。

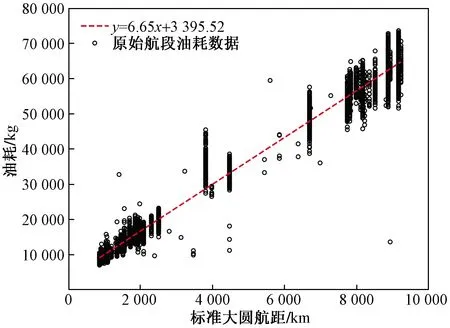
图2 原始航段油耗数据的线性回归Fig.2 Linear regression of the originalflight segment fuel consumption data

图3 异常航段油耗数据的识别和剔除Fig.3 Identification and elimination ofabnormal flight segment fuel consumption data

3.1.4 SVQR油耗估计模型的超参数寻优过程

首先对训练样本和测试样本归一化处理，据式(8)、式(9)计算得到超参数C的经验值为1.13，σ的经验范围为[0.1,0.5]，由此构建小范围、宽步长的超参数的网格如表2所示。

表2 SVQR模型的超参数网格Table 2 Hyperparameter grid of SVQR model

经5-折交叉验证后，得到超参数的初步寻优结果为C=10，σ=0.25，再经仔细调参实验，最终获得SVQR航段油耗非线性回归模型较优的超参数组合为C=10，σ=0.28。

3.1.5 对比验证

为验证本文方法的有效性，采用需假设数据先验分布的相关向量机-多项式拟合区间估计模型(relevance vector machine-polynomial fitting，RVM-PF)、最小二乘区间估计模型(ordinary least squares-interval estimation，OLS-IE)；另单独建立半参数的SVQR区间估计模型以分析SVQR模型结合Bootstrap对估计区间质量的影响情况。SVQR-Bootstrap模型，分位范围设置为0.01～0.99，分位间隔设置为0.01；Bootstrap样本数为10 000 组，每一组包含99 个抽样样本；RVM-PF区间估计模型，首先利用RVM估计出给定置信度下每一个航段油耗值的上下限，随后对上限值和下限值分别进行多项式拟合，以构建航段油耗的估计区间带，其中RVM的核函数为径向基核函数，核函数带宽设置为1，最优的多项式拟合次数为9；OLS-IE模型，首先对训练数据进行最小二乘回归，以回归值作为航段油耗的点估计结果，随后计算每一个航段油耗样本集的标准差，在正态分布假设下建立估计区间，最后对区间上下限值分别进行最小二乘回归，以构建航段油耗的估计区间带；SVQR模型则以0.025分位和0.975分位的估计值作为给定置信度下油耗估计区间的上下限，SVQR模型的核函数为径向基核函数，超参数值设置为C=10，σ=0.28。在以上设置的建模条件下，分别运行SVQR-Bootstrap、RVM-PF、OLS-IE和SVQR模型得到航段油耗的区间估计结果，如图4所示。

图4 各模型的航段油耗区间估计结果Fig.4 Interval estimated results of flight segment fuel consumption of different models

3.2 飞机航段油耗区间预测性能分析

利用测试数据集1对各模型的预测性能评价，评价指标结果如表3所示。在短航程航段，本文模型的EICP高于其他模型，表明具有较高的预测可靠性，虽然NMEIW不能保证小于其他模型，但CWC值为最小，反映出SVQR-Bootstrap模型在该航段具有较好的综合预测性能。在长航程航段，各模型的EICP均相同，但本文模型的NMEIW、CWC较高，表明在该航段上SVQR-Bootstrap模型的预测性能略低于其他模型。从总体角度分析，无论是短航程还是长航程航段，本文模型均能满足预测可靠性要求，在航空公司制定碳排放监测计划时，对于新开通的航段或完全缺失历史航班油耗记录数据的航段，使用此方法进行油耗及对应的碳排放量预测时具有较高的可靠性、稳定性。

表3 各模型航段油耗区间预测效果(95%置信度)Table 3 Interval prediction effects of flight segment fuel consumption of different models (95% confidence level)

3.3 飞机航段油耗区间估计性能分析

随机抽取短、中、长航程中各两个航段进行实例分析，利用测试数据集2对各模型的估计性能评价，结果如表4所示。

表4显示，在满足置信水平条件下，除了在标准大圆航距为4 473 km(北京首都国际机场-樟宜机场)和6 693 km(北京首都国际机场-斯德哥尔摩机场)的航段上，本文模型的NMEIW和CWC略高于SVQR模型外，从总体看来，SVQR-Bootstrap模型具有相对较高的EICP、较窄的NMEIW和较低的CWC，估计性能较优。对于标准大圆航距为3 812 km(北京首都国际机场-德里机场)的航段，各模型的EICP均低于给定置信度，特别是对于RVM-PF和OLS-IE模型，EICP值仅为0.800和0.400，原因是：在较高业载的影响下，3 812 km航段的飞机油耗普遍偏高，标准大圆航距与油耗间出现非线性关系，且该航段油耗数据呈现双峰分布特征，这时建立在正态分布假设下的RVM-PF和OLS-IE模型对该航段油耗统计量进行估计时不够合理，并且在对航段油耗上下界拟合时，由于该航段油耗上下界数据偏差较大，导致拟合效果不理想，构建的油耗估计带不够准确。此外，SVQR模型直接以不同分位点的油耗估计值作为估计区间的上下界过于强硬，未考虑航段油耗样本的分布特征，指向不明确，在3 812 km的航段上，SVQR模型的EICP仅为0.733，估计性能不佳，SVQR-Bootstrap模型利用所有条件分位估计值对油耗总体的统计量进行推断可深入挖掘航段油耗的波动范围，EICP为0.867，高于其他模型，但由于该航段样本量较少，仅有67个，在对油耗总体统计量估计时，出现一定偏差，导致在该航段上EICP低于给定置信度。

4 结论

(1)主要针对存在非规则分布特征的油耗样本的飞机燃油消耗量区间估计问题，提出了基于SVQR-Bootstrap的航段油耗区间估计方法，解决了一般区间估计方法需假设数据先验分布和拟合效果不理想的问题，通过与其他方法在不同航段上的仿真对比表明，使用该方法进行油耗估计具有较高的准确性和鲁棒性，提高了估计区间质量。可为航空公司在制定碳排放监测计划需进行油耗估计以及面向碳核查需确定上报数据的合理性时提供参考。